基于环境复杂度的危险品运输车辆碰撞预警策略

高利，戴钰，赵亚男，王显才

（北京理工大学 机械与车辆学院，北京 100081）

车辆行驶时，驾驶人感知信息和判断决策的全过程会受到运行环境的复杂程度的影响，复杂程度越大会导致工作负荷迅速增加，交通事故发生率越高，危险品运输车辆的事故发生概率虽然不及普通轿车，但是事故后危险程度却尤其之大[1]. GRABAREK等[2]通过分析危险货物运输事故数据，得出了环境复杂是造成事故的重要原因. 据此，对危险品运输车辆的运输过程进行实时可靠的数据挖掘及碰撞预警可以有效减少甚至避免重大事故的发生[3]. JIA 等[4]提出了一种基于神经网络的异常驾驶行为监测模型，有助于判断驾驶人行车风格并提前告知周围车辆避免事故的发生. 高级驾驶辅助技术的应用推广使得交通事故的数量降低了30%左右[5]，如吕能超等[6]提出了一种提升了环境适应力的基于车辆风险感知特性的以车辆运动学为基础的综合预警算法. 近年来，协同式安全驾驶的提出使得危险预警系统将不再满足于仅通过车辆当前状态判别危险状况，其试图提前捕捉周边车辆及外部环境变化，更早的为驾驶人提供预警信息[7]. 马艳丽等[8]引入了势能场理论，依据行车环境的各项参数建立了车车交互模型，为后续风险研究提供了基础；YUAN 等[9]和袁泉等[10]的研究表明，驾驶员所处的路段、时间等因素都会对碰撞风险产生影响，其基于行车安全场理论对周围环境进行评估进而建立了分级预警系统，有效地在事故之前保障了车辆和行人的安全；杨澜等[11]采用了位置、速度等多个环境指标建立了潜在预警机制，提前判定碰撞风险程度并进行预警. 郭建等[12]的研究表明，随着智慧交通技术的推广，应当将运输过程中的环境、路况等数据信息融合进危险事故状态的预判.

综上所述，文中结合危险品运输车辆自身特性及事故发生机理，提出一种结合环境复杂度和本车运行状态的危险品运输车辆碰撞预警策略，确定危险判别指标和阈值的计算方法，并利用真实数据对该策略进行有效性验证，为辅助危险品运输车辆安全完成驾驶任务提供理论支撑.

1 基于环境复杂度的危险品运输车辆预警策略

大多数碰撞预警策略的研究采用了安全距离模型及危险系数来评估当前的危险程度，并设定发出警报和采取行动的危险阈值[13]. 为了直观地反映出本车受到前车威胁的安全时间余量且更接近驾驶人的判断习惯，大部分研究采用了诸如车头时距（time head way，THW）和碰撞时间（time to collision，TTC）等表征碰撞危险的参数来模拟行驶环境中的危险程度，一部分建模方法引入了前车与本车的相对距离和相对速度，另一部分建模方法除了引入相对速度还引入了本车车速和加速度[14].

虽然随着理论的更新上述模型考虑的角度越来越全面，但是其本质依旧是将车辆看作独立的单位而忽视所处交通流及环境所造成的影响，对于事故后果严重性强烈的危险品运输车辆而言，其预警策略应当相较于普通轿车更能全面反映与周围环境及交通参与者的时空关系，故此提出了一种以环境复杂度为基础的新型预警模型.

1.1 环境复杂度量化

驾驶人所处的驾驶环境复杂度由多方面组成，包括道路信息、运行状况和其他交通参与者等，每个构成元素都具有自身的特性和运行规律，并在一定程度上影响着驾驶人对行车安全的判断和决策. 因此，环境复杂度的影响因子对事故的发生负有一定责任，这些影响因子之间相互制约、相互作用，并且对车辆造成的危险性随着行驶速度、行驶方向的变化发生变化，一般将这些因子分为静态和动态两种.

静态环境复杂度的影响因子作为客观要素影响着整体行驶环境的难易程度，是对车辆当前行驶环境的描述，求解过程需要综合各可视化要素对复杂度的影响程度，探寻其中存在的非线性联系. 而动态环境复杂度的影响因子则作为主观要素随着行驶环境的变化产生不同的影响强度，是对车辆当前变化状况的描述，需要结合动态数据进行具体分析.

1.1.1 静态环境复杂度量化

在人-车-路交通系统中，环境静态要素之间的相互协调配合是车辆安全、高效、舒适行驶的前提条件，无论是对于有人驾驶还是无人驾驶而言，静态环境会直接影响车辆的决策和操作. 大多数研究认为静态环境复杂度就是各个运行环境要素的复杂程度的总和，可以由一个要素的多种情况的构成，也可以是多种要素的相互影响. 为了准确界定和表征危险品运输车辆参与静态环境的复杂度影响因子，针对中国道路交通环境，基于交通部发布的运输货车事故发生原因进行数据分析，其要素和分布状况如图1 所示.

图1 运输货车事故发生原因及要素分布Fig. 1 Causes and factors distribution of freight car accidents

虽然事故发生情况不能直接用于复杂度的量化，但是可以用于构建复杂度的影响指标. 从危险品运输车辆的实际需求出发，在深入研究实时交通状况数据传输的基础上，遵循系统性、代表性的原则，对影响静态环境复杂度的代表性因子进行分析，形成了危险品运输车辆静态环境复杂度指标体系，如图2所示.

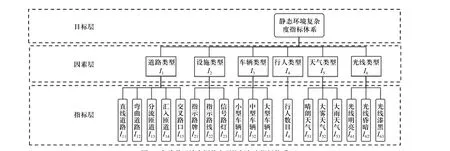
图2 危险品运输车辆静态环境复杂度指标体系Fig. 2 Index system of static environment complexity for dangerous goods transport vehicles

分析上述指标，结果表明其与静态环境复杂度之间并非清晰的数学关系，而是存在着不能直接用公式表征的更加模糊的关系. 为此，文中采用对于模糊关系拟合程度最优的BP 神经网络（back propagation neural network）对静态环境复杂度进行量化，验证此方法的可操作性并运用于危险品运输车辆的预警系统. 神经网络模型如图3 所示.

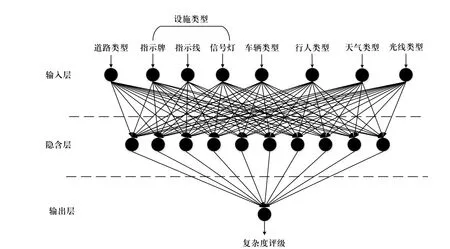
图3 神经网络模型结构Fig. 3 Structure of neural network model

将所获样本数据从输入层传递入神经网络，经过网络之间的连接函数计算并将输出值传递至下一层作为输入，经过反复迭代至输出层，完成神经网络的正向传播，数学表达式为

式中:ni为隐含层第i个节点的输入；wij为第i个节点与第j个节点的连接权值；θi为神经元的阈值；oi为隐含层第i个节点的输出；ϕ(·)为隐含层节点的传递函数；nk为输出层第k个节点的输入；ok为输出层第k个节点的输出；ψ(·)为输出层节点的传递函数.

正向传播结束后，将得到的输出结果与实际值相比较并计算误差，若误差不符合期望，则将误差信号反向传播，向着使误差不断减小的方向调整连接权值及阈值，如此反复直到误差符合期望后停止训练，数学表达式为

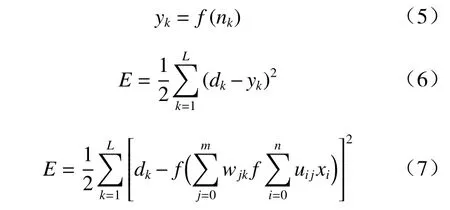
式中:yk为第k个节点的输入值；dk为第k个节点处的反向误差；E为误差函数；wjk和uij为连接权值.

误差函数以连接权值为变量，改变权值即可调节误差，当权值与误差负梯度成正比时，误差将会朝着减小的方向调节. 在神经网络训练完成之后，只需要输入指定的数据，就可以获得准确率较高的静态环境复杂度结果. 据此原理设计能够实时传输的静态环境复杂度模型，如图4 所示，在路侧设备、气象部门、高精地图的帮助下，所需复杂度指标能够被识别并上传共享，在数据离线时可以进行BP 神经网络的训练并用于线上数据的实时复杂度预测，将预测结果提前输入危险品运输车辆的预警系统，即可进行危险判别指标的计算.

图4 静态环境复杂度模型框架Fig. 4 Static environment complexity model framework

1.1.2 动态环境复杂度量化

与静态环境复杂度不同，动态环境复杂度会随着时间和距离的波动而发生变化，受到周围车辆的制约和影响. 马艳丽等[8]引用了势能场的理论给出了周围车辆对本车影响程度的变化规则：当车辆间距足够大时，势能场影响区域不会重叠，此时车辆能够自由安全行驶，车辆之间不具有交互作用；当车辆间距较小时，驾驶人将会感受到周围车辆产生的“压迫”，并采取一定措施进行远离，其中的势能场影响为

式中：x、y为以目标车为几何中心所建立平面直角坐标系的坐标；a、b为势能影响区形状参数；a依据跟驰行驶的最小车间时距而定；b与相邻车道及不相邻车道的交互区域相关.

参考势能场理论，考虑到危险品运输车辆一般质量较大、所运输的危险品有可能会出现与罐壁摩擦点火的现象[15]，不能进行短距离急刹车，所以，TTC 针对的短距离大速度差的“危险且紧急”预警功能并不适用. 文中选择了能够给予驾驶人足够反应时间，表征“危险且不紧急”预警功能的THW 计算式为

式中：s为动态环境复杂度影响因子与本车的纵向相对距离，m；v为本车当前的行驶速度，m/s.

但是由于危险品运输车辆的特殊性，为了最大程度降低事故发生的可能性以及减轻事故发生后造成的后果，需要与周围车辆均保持一定的安全距离，故还需要考虑非本车道前方的影响因子所带来的影响，避免车辆突然换至本车道. 因此将THW 公式中仅考虑纵向的距离参数s调整为考虑全局的相对距离参数，并且计算结果与动态复杂度成正比关系. 优化后的动态环境复杂度计算式为

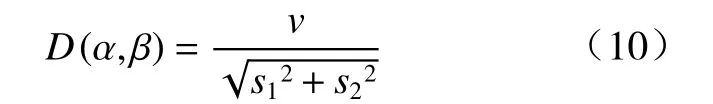
式中：D(α,β)为动态环境复杂度；s1为动态环境复杂度因子与本车的纵向相对距离，m；s2为动态环境复杂度因子与本车的横向相对距离，m.

1.2 预警策略模型

综上所述，提出的危险品运输车辆危险判定指标与当前环境的静态和动态环境复杂度成正比. 数学表达式为

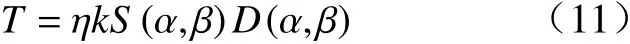
式中：T为文中提出的静态及动态环境复杂度影响因子对所研究危险品运输车辆产生的危险判定指标；η为修正参数，用于修正车辆因素及其他因素对计算结果造成的影响，但是对于同一车辆和同一工况下，此值应相同；k为主观因素对危险判定指标造成的影响系数，及驾驶员主观产生的影响，如果驾驶员处于良好状态下，k值取1；S(α,β)为静态环境复杂度；D(α,β)为动态环境复杂度.

危险判定指标T能定量反映出当前环境下驾驶人所处工况的危险紧迫程度，因此可以直接作为预警系统进行警报的有效判据. 如图5 所示，通过复杂度模型计算出静态环境复杂度值，与由速度和距离组成的动态环境复杂度一起计算出危险判定指标的具体值，当T大于所设定的预警阈值时，对驾驶人进行直接预警，提示驾驶人进行操作避免事故发生，分级预警逻辑如图6 所示.

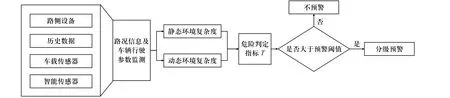
图5 基于环境复杂度的危险品运输车辆预警策略Fig. 5 Early warning strategy of dangerous goods transport vehicles considering environmental complexity

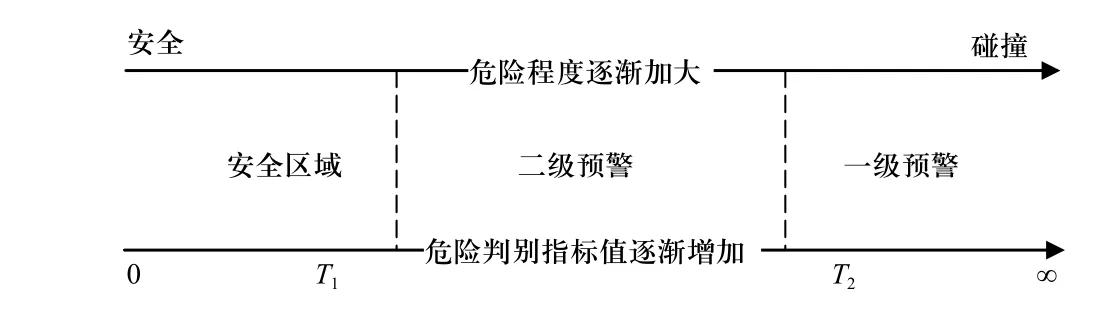
图6 分级预警逻辑Fig. 6 Hierarchical early warning logic

2 预警阈值设定

以静态环境复杂度和动态环境复杂度共同作为预警策略的判定条件，为确定危险判定指标和预警阈值之间的数量关系，现需要验证复杂度模型数据及实车标定.

2.1 实车数据收集

为还原危险品运输车辆行驶路段真实情况，针对宁波某真实危险品运输路段进行路侧信息、地图信息、气象信息收集，在其中一辆危险品运输车辆上搭载装有市面上普遍的前向碰撞预警系统的行车记录仪进行报警数据记录，某一路段行驶轨迹如图7所示.

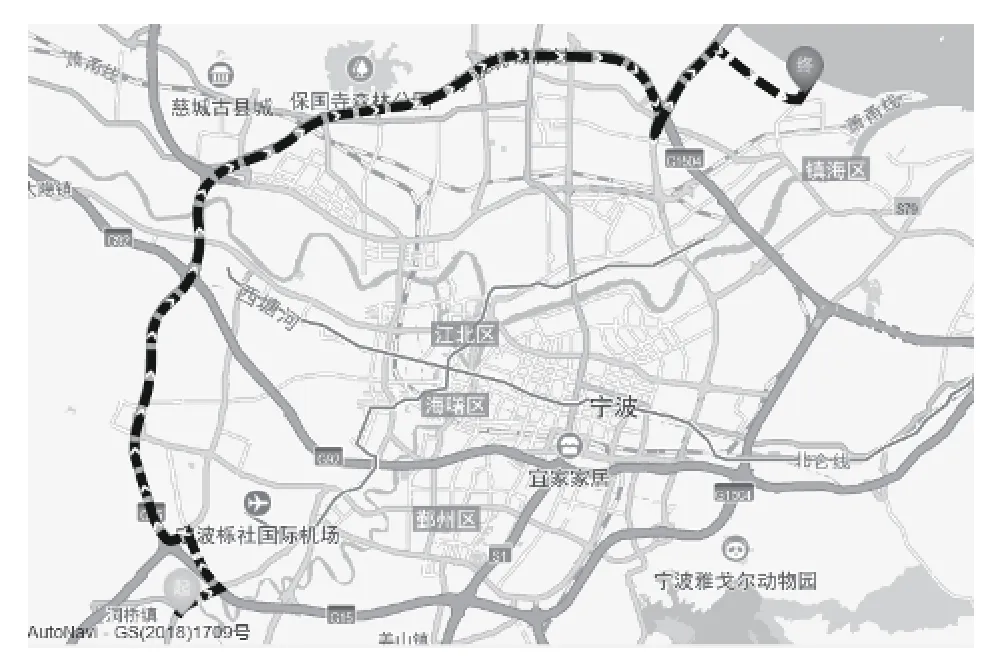
图7 实车试验路线图Fig. 7 Road map of real vehicle test

2.2 静态环境复杂度模型验证

根据所收集的信息进行静态环境复杂度模型的构建和验证，实验数据库数据来源分为两种:一种是所收集的路段数据，直接依据路侧、高精地图和气象部分所获得客观数据获得指标值，定性指标将直接赋予不同的数字表征两种状况的区别；第二种则是最终的复杂度评级，本实验一共邀请了10 位老师和同学进行相关评级，采用专家打分法进行逐一投票打分，最终去掉一个最高分、一个最低分后取平均值作为结果.

为了得到更为合理的结果，减少因为人为判断误差产生的错误率，将对复杂度进行模糊化处理，将期望输出结果定为5 个级别，即P=（最简单，较简单，普通，较复杂，最复杂），所对应的模糊化等级为P=（1,2,3,4,5）.

数据收集结束后，对所得数据进行初步分析，人为筛选出具有代表性的不同时间段和路段的典型数据，进行审阅、编号和整理，剔除重复的相似场景，最终获得2 000 个代表数据. 在Matlab 中导入已经建立好的数据集，将数据打乱进行随机排列，取1 800个数据标记为训练集，剩下的200 个数据进行验证. 反复训练神经网络，通过迭代，最大失败次数达到10 次时停止训练，输入与期望输出的拟合效果见图8，测试样本的预测输出值和实际期望值对比见图9.

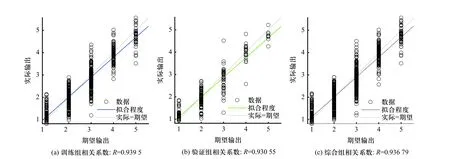
图8 高速公路模型输入与期望输出拟合效果Fig. 8 Fitting effect of input and expected output of highway model

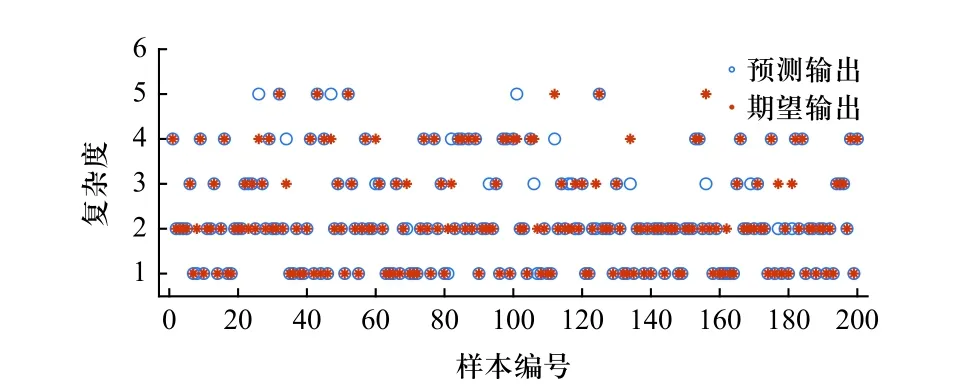
图9 测试样本的预测输出值和实际期望值对比Fig. 9 Comparison of predicted output value and actual expected value of test sample

结果表明，模型训练结束时梯度为0.063 8，预测误差为0.140 44. 图8 表明，训练组相关系数为R=0.939 5，验证组相关系数为R=0.930 55，样本输入输出的综合相关系数为R=0.936 79，取得了较好的拟合效果. 图9表明，测试样本的正确率为88%，预测输出和实际期望较为一致. 实验结果表明，所建立的静态环境复杂度量化模型能够较好实现目标，误差在可接受范围内，可以有效便捷地量化复杂度，运用于危险品运输车辆预警策略模型.

2.3 动态环境复杂度模型验证

行车记录仪所收集部分数据如图10(a)所示，当速度和距离的差值越大，动态复杂度越大，符合动态环境复杂度的计算原理.

依据式(9)计算其TTHW值，部分数据如表1 所示，结果如图10(b）所示，绘制TTHW的范围线，显示所测TTHW值在0.5～1.6 s 之间，符合基于车头时距的危险预警策略的提醒范围，证明所采用的动态环境复杂度模型与普通前向碰撞系统报警数值具有大致相同的浮动范围，能够在一定程度上表征行驶车辆所处的环境的危险性. 记录动态环境复杂度的数值范围用于预警阈值计算.

表1 部分数据的计算结果Tab. 1 Calculation results of some data

图10 部分预警数据分布图Fig. 10 Distribution of some early warning data

2.4 预警阈值设定

预警系统策略的关键就是预警时机的选择，如果不能及时发出预警信号，驾驶人可能因为注意力不集中的缘故无法规避危机；但是如果系统预警频繁，甚至在不需要注意的工况下也发出警报，则容易分散驾驶人的注意力，甚至对预警系统信任缺失.

根据上文建立的静态环境复杂度模型，当处于最简单或较简单静态环境时，驾驶人不会产生较大工作负荷，对环境的判断也比较清晰，具有足够的控制力对车辆进行安全驾驶. 但当驾驶人处于较复杂环境，例如雨天、视野不清晰、交通场景混乱等场景时，驾驶人的心理负荷将会加重，生理上也会出现疲惫、心率加快、手心出汗等一系列现象，此刻驾驶人对于车辆的判断力和控制力明显下降，容易出现驾驶失误，无法规避一些在简单环境下不会出现的驾驶风险. 这证明，在静态复杂度超过一般复杂的程度之后，驾驶人即使在处理普通驾驶任务也容易产生失误. 根据前文对危险品运输车事故发生因素的数据分析，在一般复杂和较为复杂的环境交界时驾驶人应当更为注意周围车辆的距离变化，即取S(α,β)=3.5 作为静态环境复杂度的二级预警阈值，在处于较为复杂的环境后，驾驶人则需要集中注意力，避免发生碰撞事故，即取S(α,β)=4 作为静态环境复杂度的一级预警阈值.

参照文献[16]，在危险工况中驾驶人的制动反应时间平均分布在1.02 ～1.36 s 之间，绝大多数驾驶人的在制动过程中的最大减速度为平常减速度的2 倍以上，所以目前一般的高级驾驶辅助系统中装载的前向碰撞预警系统（forward collision warning, FCW）中所设定的TTC 值最高为2 s，小于1 s 则必须采取相关行动. 而THW 值与TTC 值类似，一般采用1.5 ～2 s 作为安全和提醒的交点值，越往下代表碰撞可能性越大，直到0s 时表征碰撞的发生不可避免. 对比THW 和D(α,β)公式进行取值，考虑到危险品运输车辆的特殊性以及上文实车数据的分析情况，为了避免因为急刹车造成的运输物爆炸，取TTHW=1.7 s 时作为安全和提醒的临界值，即取D(α,β)=0.59 作为动态复杂度的二级预警阈值，取TTHW=1.5 s 时作为必须开始制动的临界值，即取D(α,β)=0.67 作为动态复杂度的一级预警阈值.

综合静态和动态环境复杂度的取值范围，理论上讲，修正参数η=0 时意味着预警过程中不具备需要提示驾驶人注意危险的场景，这样的预警规则最不理想，因此，所选修正参数η值应当根据实际环境调整使预警规则最符合驾驶人的制动方式.

根据行车记录仪所记录样例，收集驾驶人行驶状态中的放松、专心和谨慎驾驶环境数据，对数据进行静态环境复杂度和动态环境复杂度计算，如图11所示. 随着静态环境复杂度的增大，驾驶人对车辆的掌控能力下降，行车也更为谨慎，表明环境的复杂情况确实会对危险品运输车辆驾驶人的危险判断产生影响.

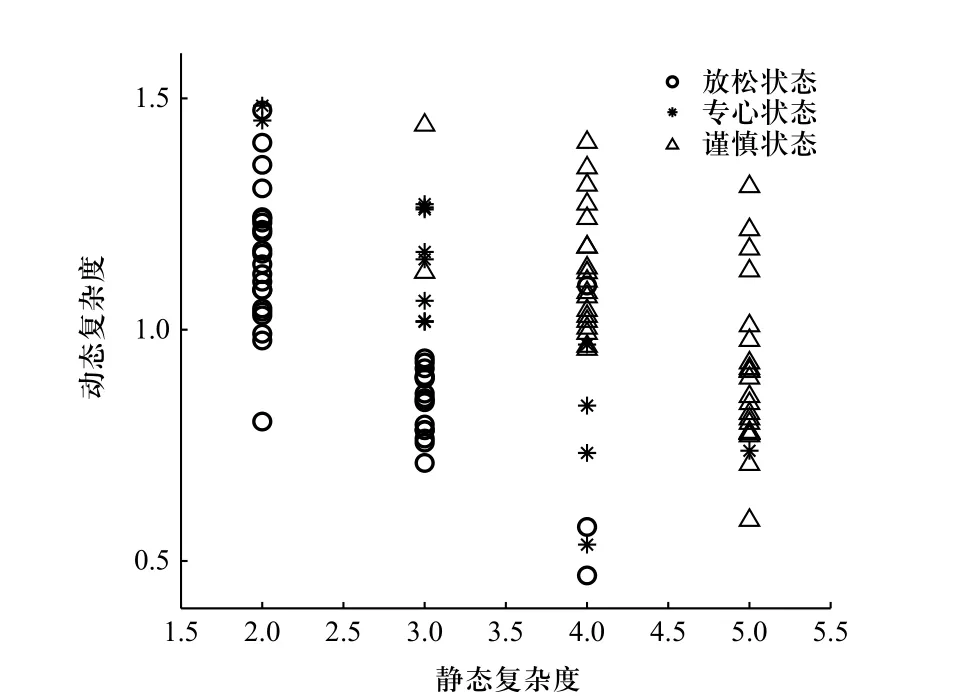
图11 预警数据的复杂度分析Fig. 11 Complexity analysis of early warning data

根据3 个状态的分布情况，经计算取η=1.42，最终确定危险判定指标与预警等级之间的对应关系如表2 所示.

表2 危险判定指标和预警等级的对应关系Tab. 2 The relationship between risk judgment index and early warning level

二级预警状态时，代表危险品运输车辆处于虽然车距较为安全但是周围环境较为复杂不易控制，或者虽然环境较为简单但是车距较为危险的状况，驾驶人需要停止加速、放松油门或者略降低车速；一级预警状态时，代表危险品运输车辆处于周围环境以及与周围车辆车距均比较危险的状况，驾驶人应当采取制动行为并小心谨慎驾驶.

3 碰撞预警策略验证

为进一步验证预警系统阈值的有效性，在宁波某危险品运输车辆行驶的同一路段采用装载了市面上普通的前向碰撞预警系统的行车记录仪收集了同一工况下危险品运输车辆不同时间的自然行驶数据，标注车辆在发出预警时的油门情况和制动情况，随机抽取了其中100 条数据进行分析.

如图12 所示，对于市面上普通碰撞系统而言，在100 次预警提醒中，其中只有59 次驾驶人感觉具有危险并采取了放松油门或踩踏制动踏板的行动，证明有时候虽然当前环境处于预警系统的预警条件中，但是对于驾驶人而言并不需要引起注意或是进行制动. 采取基于复杂度的预警策略后，预警正确次数提升至92 次，相较而言更能够表征驾驶人对于危险状况的感知规则，起到预警效果.

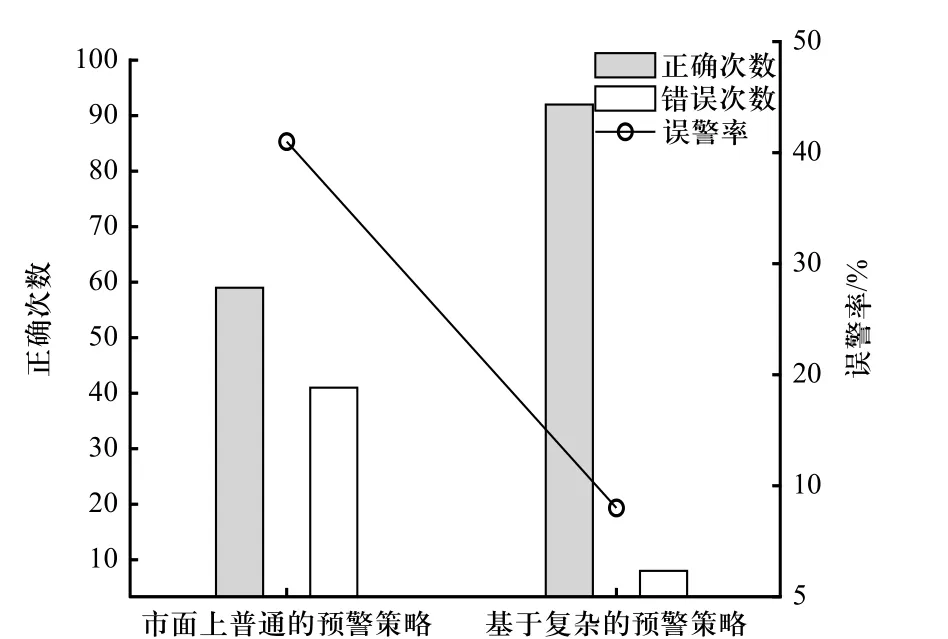
图12 预警策略验证Fig. 12 Early warning strategy verification

图13 策略对比Fig. 13 Strategy comparison

4 结 论

文中从危险品运输车辆的自身特性出发，通过分析真实运输路段数据、结合事故发生影响因素提出了危险品运输车辆静态和动态环境复杂度的计算方式，基于该计算方式设计了一种新的危险判定指标，并由此确定了危险品运输车辆的预警策略，使用实车数据验证了该策略的有效性和可行性.

经过研究可知，在低静态环境复杂度的情况下，即使是较高动态环境复杂度时驾驶人也偏向激进驾驶，但随着静态环境复杂度的增加，驾驶人对于环境是否危险的判断力与敏感性都发生了明显变化，驾驶风格变得谨慎保守. 根据此机理，提出了基于环境复杂度模型的预警策略，并通过神经网络的方法对静态环境复杂度进行量化，避免了权重的繁琐计算.通过实车验证，所获策略相较市面普通预警系统误警率从41%降低至8%、且预警机制分类更加符合驾驶人的判断习惯及危险品运输车的独有特点，分类后的平均正确率达到92%，取得了较好的预警效果. 该研究顺应技术发展方向，采用了智慧交通的概念，为辅助危险品运输车辆安全提供了新思路.

环境复杂度应用于车辆碰撞预警研究领域尚处于尝试阶段，所提出的危险判别指标和复杂度量化方法为相关研究提供了一定参考，受目前试验条件所限，所研究指标和路段特征能否实际应用于所有危险品运输车辆并推广至其他区域值得商榷，后续将对危险判别指标公式进一步分类讨论，针对更为复杂的时空关系进行研究，使其更加适应实际道路交通中的驾驶环境.