基于FFRLS-AEKF 的6 轮足机器人电池SOC 估计

汪首坤，鲁帅，陈志华，刘道和，岳巍,3

（1. 北京理工大学 复杂系统智能控制与决策国家重点实验室，北京 100081；2. 北京理工大学 伺服运动系统驱动与控制工信部重点实验室，北京 100081；3. 北京新能源汽车股份有限公司工程研究院试验中心，北京 100176）

对于移动机器人而言，能源管理技术始终是其续航问题的重点和难点[1]. 在整个能源系统中，动力电池的剩余电量直接决定了电动机器人的工作时间，而锂离子电池的荷电状态（state of charge，SOC）对于电动机器人的剩余电量有着指导作用[2]. 同时，对于纯电动的机器人来说，精确的SOC 估计是保证动力电池在安全区间内充电和放电的主要依据，是保障动力电池安全性的重要手段，是延长锂电池寿命的重要参数[3].

由于电池内部复杂的化学反应，SOC 始终处于非线性的时变过程，故不能直接测量计算，只能通过电池的外特性参数估计得出. 目前主流的SOC 估值方法有开路电压法（open circuit voltage，OCV）、安时积分法、神经网络法、内阻测试法以及卡尔曼滤波算法等[4−5]. 开路电压法和内阻测试法都是利用动力电池的特征参数，内阻法是基于阻抗谱的方法测试出不同SOC 下的电池内阻，提取SOC 特征参数，建立SOC 和该参数之间的函数关系，用查表方法标定SOC. 开路电压法是实验室测试的常用方法，通过建立OCV-SOC 的映射关系以达到估计目的，许多BMS厂商也使用这种方法来粗略的标记电量. 但是OCV的测量需要动力电池处于开路状态，并长时间放置，不适合在线估计. 安时积分法基于SOC 的定义，只考虑电流和时间两个变量，简单准确. 但在实际中，电流传感器受随机扰动影响，精度有限，在积分运算中，这些扰动量会造成累加误差[6]，同时由于动力电池的SOC 初值难以确定，故该方法常与其他方法组合.神经网络算法对模型依赖较低，但需要庞大的数据训练集，同时算法的复杂度较高，现有嵌入式单片机大多无法满足估计运算的实时性. 卡尔曼滤波算法可以在历史数据不完善的情况下，通过迭代运算对SOC 作出准确估算，其对电池模型的的依赖比较强，且不能估计非线性时变系统的状态. SUN 等[7]利用扩展卡尔曼滤波算法(extended Kalman filtering，EKF)对剩余电量进行估算，但使用模型的RC 参数是通过离线辨识得到的，忽略了参数会随着电池的充放电循环而变化；ZHU 等[8]通过使用状态监测电路测量动力电池的开路电压，再根据开路电压和SOC 之间的映射关系估计SOC，但该方法需要将监测电路和被测试电池连接到一起，系统配置复杂；YANG 等[9]使用改进型的卡尔曼滤波算法，并在线辨识模型参数，考虑到了电池内部的动态特性，但是其电池模型为1 阶RC 模型，不能充分反映出锂电池内部的极化效应.

综合上述方法对电池SOC 估计的优点和不足，并结合6 轮足机器人在做轮足复合运动以及轮式、足式步态切换时电流变化剧烈的特点，以6 轮足机器人动力锂电池包为对象，基于动力电池的2 阶RC模型，将带遗忘因子的递推最小二乘(recursive least squares with forgetting factor，FFRLS)与自适应扩展卡尔曼滤波(adaptive extended Kalman filtering，AEKF)算法相结合，联合估计电池模型参数和SOC，并在动态应力测试(dynamic stress test, DST)工况下，对算法进行了实验验证，结果表明本算法具有较高的估计精度.

1 6 轮足机器人动力系统

6 轮足机器人具有多运动模式、负载重量大和环境适应性强的优点，主要由主控系统、环境感知系统、能源管理系统和驱动执行机构组成[10].

能源系统由动力电池系统和控制电池系统两部分组成. 本文的研究是基于机器人的动力电池部分，动力电池主要包括7 个电池模组，每个模组由12 个50 A·h 的电芯串联而成，负责给6 轮足机器人的36 个400 W 的足式电机和6 个1 200 W 的轮式电机供电.机器人动力系统如图1 所示，动力电池参数如表1 所示.

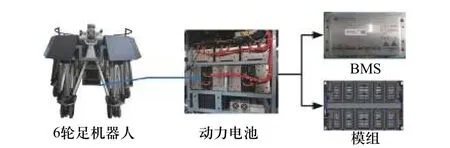
图1 机器人动力系统结构Fig. 1 Robot power system structure

表1 动力电池参数Tab. 1 Parameter model of power battery

2 电池等效模型与参数辨识

2.1 等效模型建立及离散化处理

电池建模是为了确定电池的环境参数与各特征量之间的数学关系. 一个良好的电池模型需要准确地反映出电池的动静特性，并且模型不过于复杂，易于仿真计算，同时在工程上便于实现[11]. 本文综合了Thevenin电路模型和GNL 电路模型得到二阶RC 等效模型，模型由2 个RC 回路和1 个电阻组成，如图2 所示.

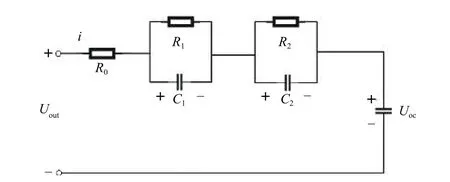
图2 2 阶RC 等效电路模型Fig. 2 Second order RC equivalent circuit model

Uoc为理想电压源，代表电池的开路电压（OCV），R0为欧姆内阻，R1为电化学极化电阻，C1为电化学极化电容，用于描述电化学极化现象，R2为浓差极化电阻，C2为浓差极化电容，用来模拟浓差极化过程；i为电池电流，定义充电为正，放电为负；Uout为电池端电压. 虽然2 阶RC 模型未考虑电池的自放电效应，但与1 阶模型相比，能更准确地描述锂电池的动态特性，相比于更高阶的模型，在精度损失比较小的前提下，减少了运算量.

根据电流定律(KCL)和基尔霍夫定律(KVL)，可推导参数关系如下

2.2 OCV-SOC 关系建立

电池电动势（electromotive force，EMF）是电池的一个重要参数，推导出SOC 和EMF 的函数关系，对解析电池的内部状态有重要作用[12]. 由于EMF 无法直接测量，所以OCV 来替代EMF 进行计算和实验.为得到动力电池OCV 与SOC 的映射曲线，进行了脉冲式充放电试验，首先恒流恒压将电池充满，然后以1 C 的电流放电，使SOC 减少至95%，放置3 h，待极化反应消失，可以得出当前SOC 下稳定的OCV 值.反复以上的充电和放置周期，直至达到表1 中动力电池的放电截止电压. 充电试验与放电试验原理基本相同，只是电流方向相反.

由上述试验分别得到了OCV 和SOC 随时间t函数关系，数据表明，该锂离子电池在相同SOC 的情况下，充电和放电的开路电压存在一定的差异，充电OCV-SOC 曲线略高于放电曲线，该现象为锂电池的电压迟滞效应. 本文选取了SOC 从0～100%共13 对数据点，采用Matlab 中的cftool 函数拟合得到6 阶方程如式(5)所示，拟合之后的曲线能较好地弥补充差异，所以研究过程中忽略了迟滞效应. 拟合曲线和实验数据的对比结果如图3 所示.

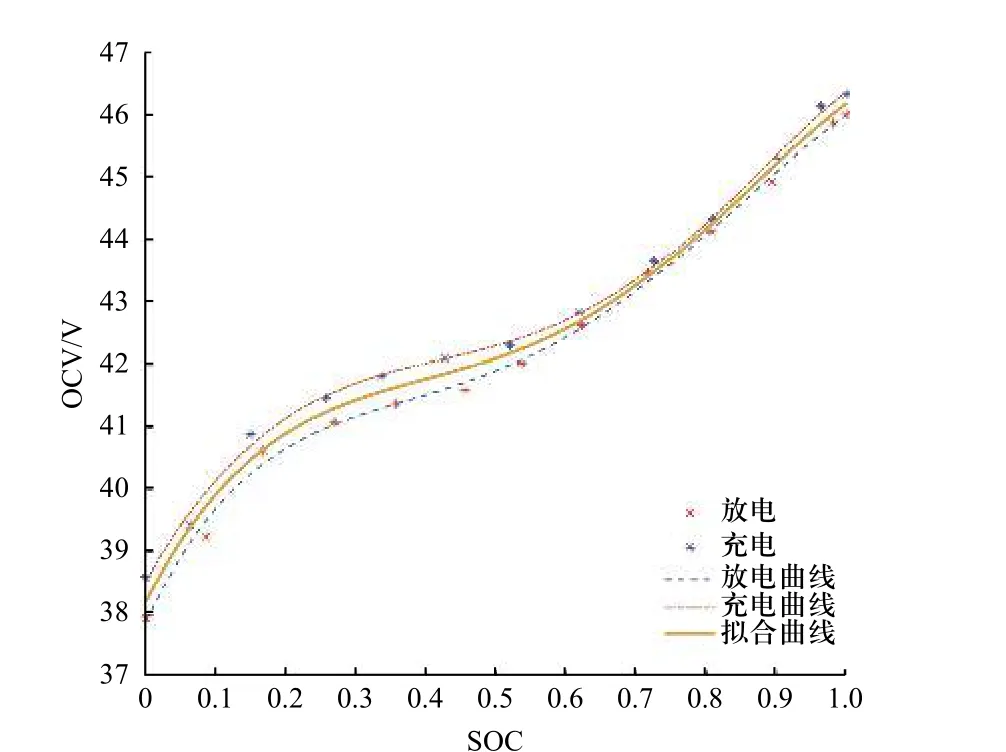
图3 SOC-OCV 拟合曲线Fig. 3 SOC-OCV fitting curve

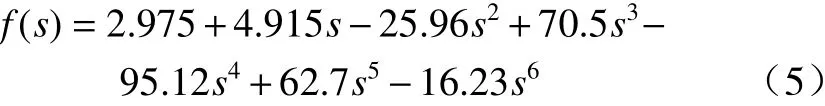
式中；s为 SOC 值；f(s)为OCV 与SOC 的函数关系.

2.3 基于遗忘因子递推最小二乘的在线参数辨识

锂电池在充放电过程中内部有复杂的电化学反应，随着电池SOC、电池老化程度和外界温度等条件的改变，模型的参数也会发生较大变化. 因此为了提高估计SOC 的精度，增强系统的适应性，需要对模型参数进行在线辨识和实时校正. 在诸多参数辨识方法中，最小二乘法以其结构简洁和快速收敛而被广泛使用于系统识别场景中[13]. 基于最小二乘法的参数在线辨识能根据得到的电池状态，实时计算模型参数，使得电池模型能够更加符合当前时刻的电池特性，从而提高了模型的准确性.

含遗忘因子的递推最小二乘法原理如式(6)所示

因为难以通过几次计算就使得估计值接近真实值，故引入了递推算法来完成对系统的辨识. 又由于递推最小二乘法的记忆长度是无限的，所以随着递推步数k的累加，积累的历史数据会不断增加，旧数据会使矩阵方差P(k)和增益K(k)越来越小，这使新得到的数据难以起到修正的效果，而且在时变系统中，这种情况更为严重. 因此，FFRLS 算法增加了遗忘因子 λ来削弱前面递归数据的作用，避免了“数据饱和”的问题[14]. 同时，遗忘因子 λ也决定了算法的收敛速度和模型的跟踪能力.

3 电池荷电状态估计

3.1 扩展卡尔曼滤波器原理

卡尔曼滤波器(Kalman filter,KF)在滤波器中引入了状态空间表达式，利用上一时刻的状态向量估计值和当前时刻的输出观测值，迭代求出当前时刻的最优状态估计，同时更新协方差，修正系统增益，不断地修正状态变量，使估计结果趋于真实值. 但是卡尔曼滤波算法只适用于线性系统，对非线性系统，扩展卡尔曼滤波算法(EKF)将系统的非线性部分进行泰勒多项式展开，并忽略高阶项的误差，即将系统线性化，进而运用卡尔曼滤波法进一步分析计算.

对于任意的非线性离散模型可表示如下

由式(19)～(24)可以得出，扩展卡尔曼滤波算法与普通的卡尔曼滤波器相比，计算状态估计时使用了非线性状态方程；计算系统输出向量的估计值利用了非线性观测方程；滤波过程是以连续地“预测-修正”的递归形式进行计算，首先计算预测值，然后利用卡尔曼增益以及观测得到的新数据，对预测值进行纠偏. 由滤波值得出预测值，再由预测可以得到滤波，二者相互作用，能够实时运算，不必存储任何数据.

3.2 自适应扩展卡尔曼滤波算法

在动力电池这样的非线性系统中，EKF 应用广泛. 但是，在初值设置不当的情况下，线性化误差可能会导致结果发散. 同时，实际过程中系统的噪声数是未知的，而机器人的动力电池系统受到外部温度、自身震动等因素的影响，噪声的统计数据是连续变化且不可预测的.

在状态估计时，AEKF 算法利用每一时刻观测数据的变化，同时修正和估计系统的过程噪声和测量噪声，使得估计算法中的噪声统计能够随着估计值的变化自适应更新.

3.3 FFRLS-AEKF 联合估计算法

图5 实验平台结构Fig. 5 Structure diagram of experimental platform

在2.3、3.1 和3.2 节中详细推导了带遗忘因子的递归最小二乘算法(FFRLS)和自适应扩展卡尔曼滤波算法(AEKF)的实现细节. 利用FFRLS 算法对电池等效模型中的R0、R1、R2、C1和C2做循环在线辨识，将辨识的模型结果用于AEKF 的状态估计，由AEKF算法估算出当前的SOC 值，再通过OCV-SOC 映射曲线来获取对应的Uoc，再用于下一时刻的模型参数辨识，循环递推即可得到任意时刻的模型参数值和电池SOC 估计. 递推过程实现了SOC 估算和参数识别的闭环修正，提高了整个系统的精度和鲁棒性. 该算法流程图如图4 所示.

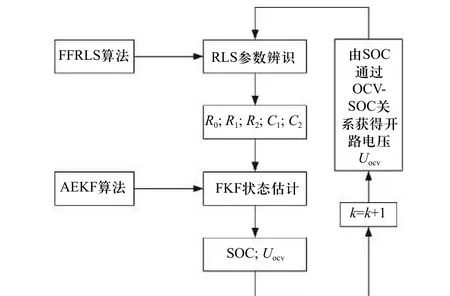
图4 基于FFRLS-EKF 的SOC 估计算法Fig. 4 SOC estimation algorithm based on FFRLS-EKF

4 实验验证

4.1 实验平台及过程

为了验证FFRLS-AEKF 联合估计算法对6 轮足机器人动力电池SOC 估计的效果，选取了6 轮足机器人的动力电池包为实验对象，在Matlab-RTW 实时仿真平台利用CAN 总线与锂电池的电池管理系统(BMS)通信. RTW 是Matlab 中一个补充功能模块，可以从Simulink 模型生成可移植的C 代码. 基于图4 的算法流程图，首先在Simulink 中搭建FRLS-EKF 估算模型，然后在RTW 平台上生成对应的代码，利用CAN 总线设备与锂电池的BMS 主控建立通信，并解析CAN报文获取充放电数据，为下一步的数据分析奠定基础.

4.2 实验结果及分析

由于6 轮足机器人在进行轮足复合运动和轮式、足式步态切换时，动力电池的瞬时电流变化幅度较大，且系统输入量要求为持续激励，故实验采取DST工况作为动力电池的电压、电流激励，Matlab-RTW通过CAN 总线通信获取充放电数据，从而进行参数辨识和SOC 估计. 动态应力测试试验电压和电流随时间变化曲线如图6 和图7 所示.

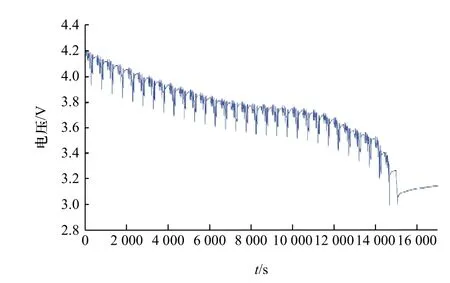
图6 DST 工况电压曲线Fig. 6 Voltage curve of DST operating condition

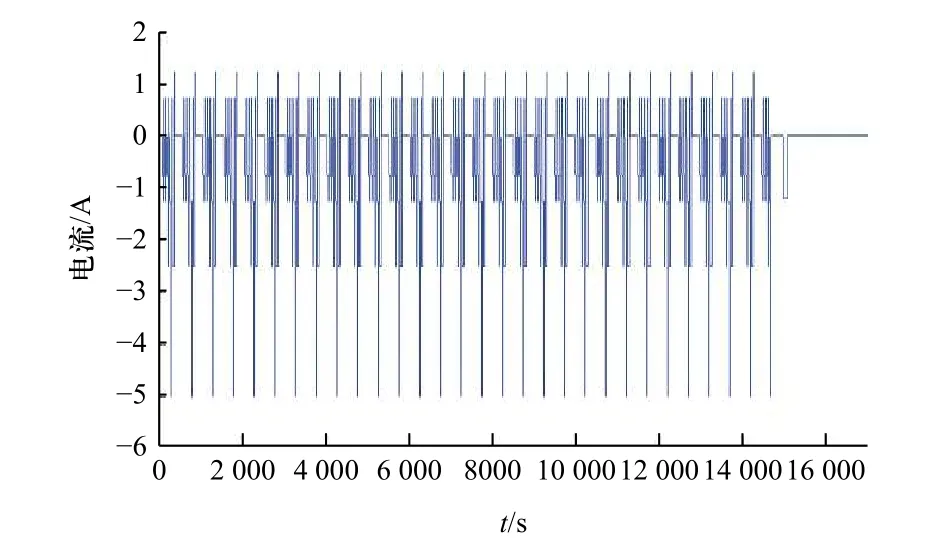
图7 DST 工况电流曲线Fig. 7 DST operating current curve

由DST 工况实验数据，并结合FFRLS 算法原理进行电池等效模型的在线辨识，选择电压变化相对稳定的区间分析处理，得到锂电池辨识参数. 2 阶RC 模型中各个参数变化曲线如图8～图12 所示.

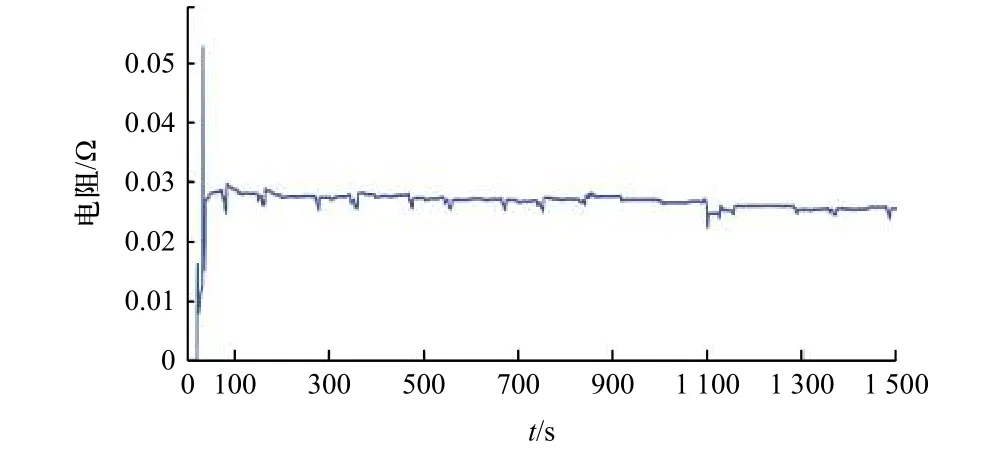
图8 欧姆内阻 R0辨识结果Fig. 8 Identification results of ohmic internal resistance R0

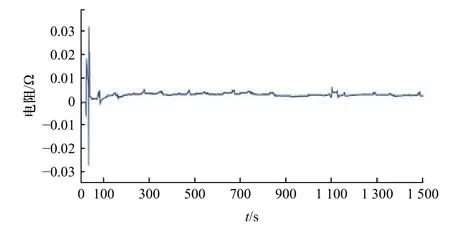
图9 扩散电阻 R1辨识结果Fig. 9 Identification results of diffusion resistance R1

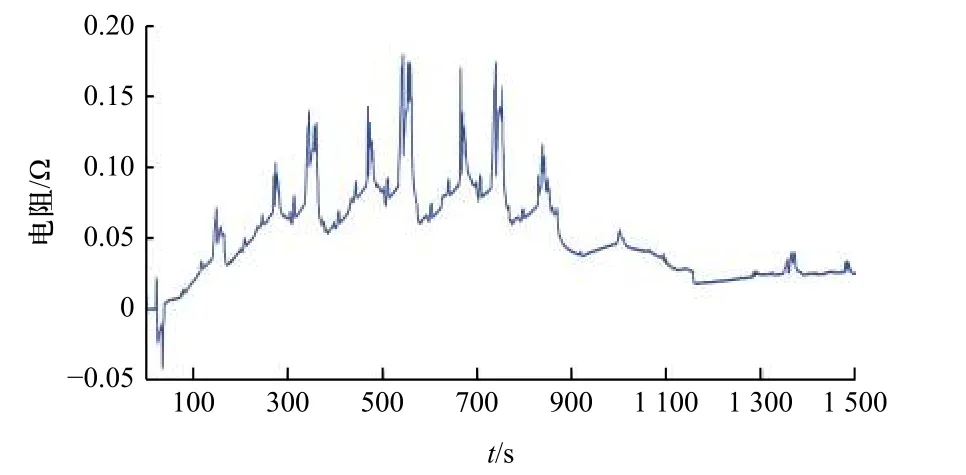
图10 极化电阻 R2辨识结果Fig. 10 Identification results of polarization resistance R2

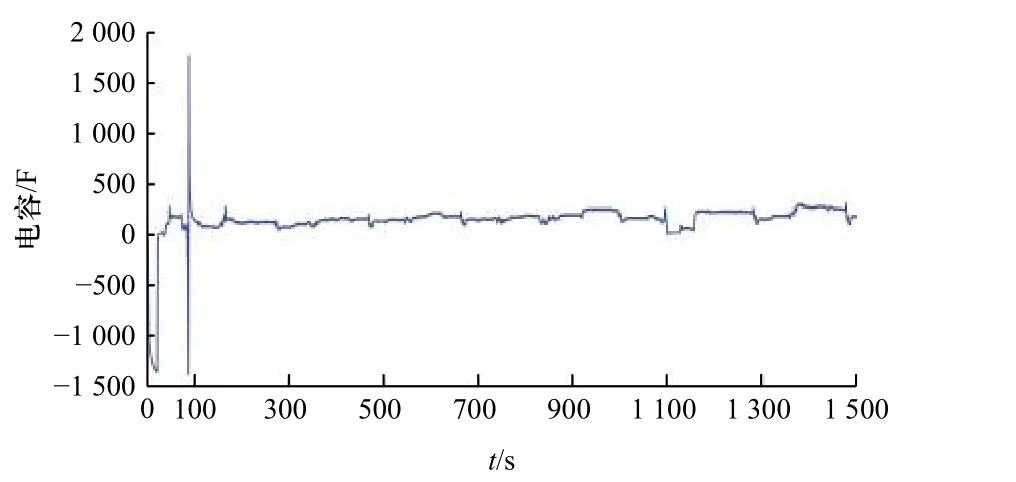
图11 扩散电容C 1辨识结果Fig. 11 Identification results of diffusion capacitance C1

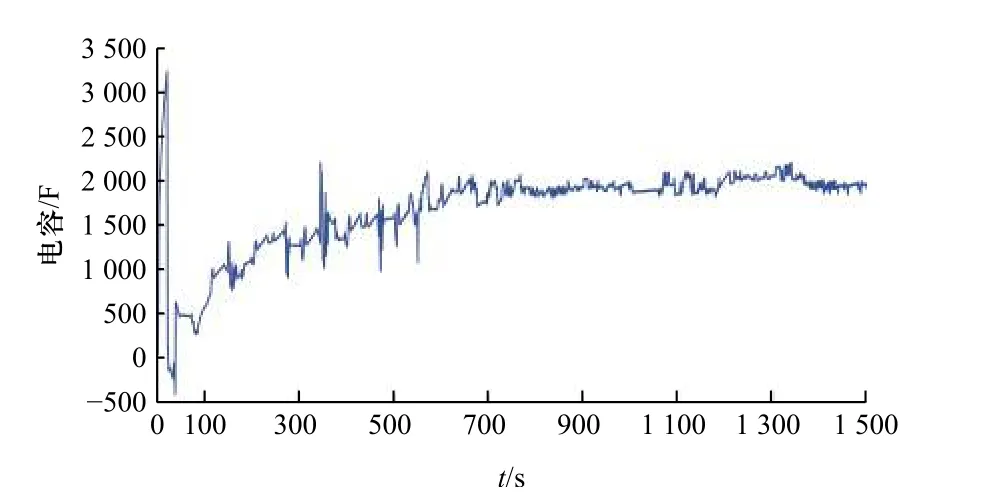
图12 极化电容C 2辨识结果Fig. 12 Identification results of polarization capacitance C2

在DST 工况下辨识的前一阶段，各个模型参数变化较为剧烈，在辨识的中后期参数辨识值逐渐平缓，此时参数较为准确. 根据所得的动态参数R0、R1、R2、C1和C2，能实时更新对应工况下电池模型的参数，可以使原有的静态模型动态化，电池模型转变为时变系统，为准确估计电池SOC 打下基础.为了验证本文方法对电池SOC 的估计精度，在DST 工况激励下，采用AEKF 算法利用在线辨识得到的模型参数进行SOC 估算，并显示算法估计模型SOC 结果与实际值的对比情况. SOC 的实时真实值是难以获取的，本文以OCV 50 V 表示SOC 为1，36 V表示SOC 为0，利用6 轮足机器人动力电池的BMS实时采集对应时刻的电流值，在此基础上，再根据安时积分法计算对应端电压的SOC，以此作为真实值.对比结果如图13，估计误差如图14 所示.

图13 SOC 估计结果对比Fig. 13 Comparison of SOC estimation results

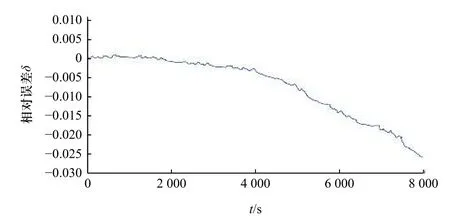
图14 SOC 估计误差Fig. 14 Estimation error of SOC

由图13 和图14 可知，在实验工况下，SOC 的估计值能够随真实值的变化而变化，并且伴随着一定波动，由于AEKF 算法能不断地获取系统的噪声信息，从而使得估计结果更加准确，使误差保持在2.5%以下. 由于算法中默认的SOC 值为1，但是实际的SOC 并不为1，导致新息误差矩阵较大，并会出现SOC 大于1 的现象. 在实际使用过程中，随着充放电循环次数增多，SOC 初值的偏差都会造成SOC 估计时初期的波动.

5 结 论

为解决传统估计方法在实际估算电动机器人SOC 中误差较大的问题，本文以6 机器人能源系统中动力电池包为研究对象，在2 阶RC 等效电路模型的基础上设计了FFRLS-AEKF 算法. FFRLS 算法在线估计电池模型参数，并且把实时的参数反馈到AEKF 算法. 通过在DST 工况下进行充放电实验，实验结果分析表明，FFRLS 算法能在负载电流频繁波动的工况下实现参数的准确辨识，适用于6 轮足机器人的实际工况，AEKF 能够提高电池SOC 的估计精度，并且在后期模型存在一定误差时跟踪模型状态，发挥自适应性的特点.