基于颗粒流法研究混凝土的劈裂拉伸破坏特性

王一阳，任会兰，宋水舟，宁建国

（北京理工大学 爆炸科学与技术国家重点实验室，北京 100081）

混凝土是当今用途最广泛、使用量最大的建筑材料，同时其物理尺度涵盖了从纳米到米的范围，是一种包括水泥砂浆基体、骨料以及二者交界面在内的三相复合材料[1]. 混凝土等脆性材料存在着严重的拉压不对称性，其拉伸强度一般远小于压缩强度，导致材料结构实际使用过程中经常由于抗拉性能的薄弱而产生破坏[2]，因此探究混凝土材料在拉伸载荷作用下的破坏过程及细观损伤机理，对提高混凝土材料的使用效率以及充分发挥材料强度具有重要意义[3−4].巴西圆盘劈裂实验是一种简单又有效的测量脆性或准脆性材料抗拉强度的实验方法. 因此，可以通过巴西圆盘实验，对混凝土在拉伸载荷作用下的破坏过程及损伤机理进行研究. 过往的研究表明，混凝土的变形破坏过程实质上是内部微裂纹产生、扩展和汇合的过程[5−6]，通过力学实验只能近似反映混凝土的宏观力学性能，而不能精确地揭示其裂纹扩展方式及混凝土各相性质对宏观力学性能的影响，所以非常有必要从细观力学角度对混凝土进行研究.

细观数值模拟是研究混凝土破坏过程的一种有效手段. 当前，细观力学数值模拟分析方法主要有连续介质分析方法和非连续介质分析方法，在常用的连续介质分析方法中，基于随机数学理论建立的混凝土随机骨料模型[7−8]，因考虑了骨料在水泥砂浆基体中分布的随机性及骨料级配问题而得到了广泛的应用.在运用该方法时，粒径最小的骨料的网格划分，往往决定了计算该模型所需的时间及网格质，为节省计算时间，很多研究中只对较大的骨料单独建模而尺寸较小的骨料简化为水泥砂浆基质，在对混凝土破坏过程进行研究时，这一简化会造成一定的误差[9]. 水泥砂浆与骨料的交界面(ITZ)作为混凝土材料中最薄弱的区域[10]，是在对混凝土破坏过程进行研究时无法回避的问题，研究表明，ITZ 厚度介于20～100 μm 之间[11]，若采用有限元等连续介质方法进行计算，往往由于试样尺寸与ITZ 尺寸之比太大而无法对ITZ 进行精确建模. 任朝军等[12]建立了混凝土二维细观有限元模型，采用最大拉应力准则及线性摩尔-库伦准则对混凝土在单轴拉伸及单轴抗压实验中的破坏过程进行了研究，作者认为无论受拉或受压，混凝土的破坏均发生在交界面上，该研究中，将界面厚度设置为骨料颗粒半径的0.1 倍，与ITZ 实际尺寸相差较多.刘建南等[13]运用有限元方法，研究了ITZ 性质对混凝土劈裂拉伸性能的影响，结果表明ITZ 界面强度及厚度均会影响混凝土的劈裂强度. 为保证计算效率，在该研究中，将ITZ 尺寸设置在0.1～1.0 mm 之间.

应用基于二维颗粒流方法的PFC2D 软件对混凝土的破坏过程进行数值模拟研究，则可以避免以上问题. HAERI 等[14]运用PFC2D 软件，不考虑混凝土的多相性，将其简化为均质模型，通过数值模拟及实验对比了不同类型拉伸实验所得的混凝土拉伸强度，结果表明改进拉伸试验所得结果与直接拉伸实验结果最为接近. 许尚杰等[15]和宿辉等[16]运用PFC2D 软件中的clump 技术随机生成刚性不规则块体来模拟粗骨料，并基于此，分别计算了混凝土在单轴压缩条件下不同细观参数对生态混凝土的破坏过程的影响.在实际混凝土结构中，粗骨料的分布形式对混凝土的宏观力学性能及裂纹扩展过程具有不可忽视的影响，而且在混凝土的破坏过程中，经常可以观察到粗骨料的破坏. 因此，为了更深刻地了解混凝土破坏的细观机理，需要在已有研究的基础上对混凝土的PFC2D 模型进行进一步优化.

本文基于PFC2D 平台，构建了二维混凝土颗粒元模型，基于该细观模型，研究了粗骨料分布形式对混凝土劈裂拉伸强度的影响，展现了混凝土在巴西劈裂实验中从损伤到发生宏观破坏的全过程，并说明了巴西劈裂实验中混凝土的细观损伤机理.

1 混凝土圆盘的颗粒流模型

二维颗粒流数值模拟方法是一种基于刚性圆盘(2D)和球体(3D)的非连续介质分析方法，用于颗粒材料力学性态分析，如颗粒团粒体的稳定、变形及本构关系，专门用于模拟固体力学大变形问题.

1.1 混凝土随机骨料模型

为了实现混凝土巴西圆盘的颗粒流模拟，首先应建立二维混凝土颗粒流模型. 为便于骨料模型的生成，将直径小于5 mm 的组分归结为水泥砂浆，本次实验采用的骨料粒径范围为5～10 mm. 依据拉瓦文公式（1），多边形粗骨料所占面积分数为16.6%.

二维骨料生成步骤可归纳为以下三步：

①在计算域内填充离散小球单元.

在选定的计算区域内，生成随机分布的颗粒，颗粒平均半径为0.25 mm，最大最小半径比为1.5，初始孔隙率为0.08.

②确定不规则多边形骨料的投放位置及形状参数.

本文中，随机多边形骨料通过对圆形进行内接切割生成，首先生成满足粒径要求的随机圆形，多边形骨料的投放位置即为随机圆形的位置，粗骨料半径介于2.5～5.0 mm 之间，根据马特螺旋算法(Mersenne Twister)，生成一系列大小介于2.5～5.0 mm 之间的随机数作为圆形半径.为保证骨料不超过模型边界，随机圆形的圆心坐标需满足以下条件：

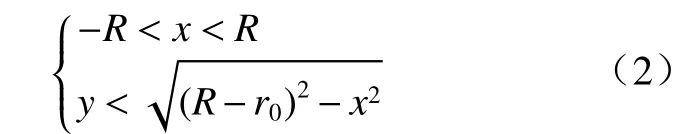
式中：x，y为生成圆形骨料的圆心坐标；r0为圆形骨料的半径；R为巴西圆盘半径.

如图1 所示，在生成多边形随机骨料时，为保证生成的多边形骨料大小满足级配要求，在生成的圆形骨料边界上选取任意一条直径AB与圆的两个交点作为骨料粒径的标定点，在直径AB两侧随机选取N个点(4≤N≤6)，顺次连接各点，形成内接于圆的多边形.

图1 多边形骨料示意图Fig. 1 Schematic diagram of polygonal aggregate

③生成不规则多边形骨料的PFC 模型

依据生成的多边形顶点坐标，在AUTOCAD 中生成多边形骨料的几何图形，将其导入PFC2D 中生成骨料边界(wall)，在此范围内投放颗粒，生成不规则多边形骨料的PFC 模型. 对生成的二维骨料的面积进行计算，圆盘的总面积为244 544 pixels，不规则多边形骨料的面积为37 809 pixels，面积分数为15.5%，基本满足拉瓦文公式.

图2 为生成的混凝土CAD 模型及PFC 模型，直径为100 mm，共包含36 331 个颗粒，其中灰色部分为水泥砂浆颗粒，蓝色部分为骨料内部颗粒，ITZ 没有实体颗粒，通过砂浆颗粒与骨料颗粒之间的接触进行定义，通过接触模型来体现其力学性质，ITZ 可以用图2(b)中的黑色短实线表示.

图2 混凝土随机多边形骨料细观模型Fig. 2 Mesoscopic model of concrete random polygonal aggregate

1.2 颗粒流接触模型

在PFC2D 中，材料是由在接触处相互作用的刚性圆盘或簇颗粒组成的，材料的本构特性是通过接触本构模型来模拟的.本文选择Potyondy 提出的平节理模型（flat joint contact model，FJM）作为接触模型，FJM 结构如图3 所示，该模型的虚拟交界面是分段的，黏结键在达到破坏条件之后，虚拟交界面上的黏结键不会被删除，而转变为不提供黏结强度但仍提供摩擦的模式，故仍可以对颗粒间的旋转运动进行约束，让模拟中的裂纹不容易闭合.

图3 平节理接触模型示意图Fig. 3 Schematic diagram of flat joint contact model

1.3 平节理模型参数

混凝土的细观模型中包含了水泥砂浆、骨料和ITZ 界面，颗粒流数值模拟中，通过参与接触的颗粒所属组分来判断此接触的属性. 如参与接触的两颗粒均为骨料单元时，则将此接触定义为骨料内部接触；如参与接触的两颗粒均为水泥砂浆单元时，则将此接触定义为水泥砂浆内部接触，如参与接触的两颗粒分别为骨料和水泥砂浆单元，则定义为ITZ接触.

表1 混凝土各组分的平节理接触模型参数Tab. 1 Parameters of the flat joint contact model of concrete components

图4 是三组使用细观参数进行颗粒流模拟所得混凝土巴西圆盘应力-应变曲线与实验结果的对比，通过模拟得到的曲线与实验曲线的相关系数分别为0.972、0.969、0.941，均较为真实地还原了实验的情况.

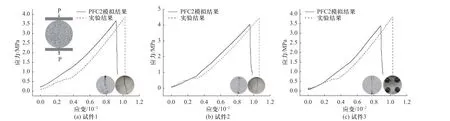
图4 应力-应变曲线的模拟结果与实验结果对比Fig. 4 Comparison of simulation results and experimental results of stress-strain curve

2 混凝土劈裂破坏的数值模拟

2.1 骨料分布对力学性能的影响

由于混凝土材料中的骨料分布具有随机性，骨料分布会对混凝土的力学性能及断裂形态产生影响，为此，在本节首先对4 种不同骨料分布情况下混凝土破坏形态进行模拟，4 种骨料分布如图5 所示.

图5 4 种随机骨料分布的计算模型Fig. 5 Four models of random aggregate distribution

0.01 m/s 的加载速度下进行模拟试验，4 组骨料分布的混凝土试件的破坏形态如图6 所示，其中红色短实线代表拉伸型裂纹，绿色短实线代表剪切型裂纹. 由图可见，混凝土试件的劈裂破坏主要是由水泥砂浆内和骨料周围裂纹产生、扩展和汇合引起的，而由于骨料分布不同，裂纹扩展路径并不相同. 此外，由图6 中可见，剪切型裂纹大量分布在加载附近的水泥砂浆中，而试件产生劈裂破坏的宏观裂纹则以拉伸型裂纹为主体；极少数的裂纹发生在骨料内部（如BD-1）； BD-2 的加载端主要为水泥砂浆， BD-3的加载端在加载方向上分布有骨料，两者最终裂纹的分布也存在着差异.如图7 所示，BD-2 的加载端裂纹数量更多且分布更为密集，加载端附近的骨料周围的裂纹主要分布在ITZ 区域内. 而对于BD-3，由于骨料直接分布在加载端的轴线位置上，裂纹沿轴线方向贯通骨料，与水泥砂浆内的裂纹取向一致.

图6 4 种随机骨料分布下试件破坏形态的计算结果Fig. 6 Four failure modes of specimens with randomly distributed aggregates

图7 加载端附近裂纹分布情况Fig. 7 Crack distribution near the loading platen

提取最初生成的混凝土试件模型（BD-0）以及以上生成的3 个随机骨料混凝土试件模型（BD-1、BD-2、BD-3）的应力应变曲线，如图8 所示. 混凝土的破坏正是由于存在的各种缺陷引起的，裂纹首先在这些缺陷部位萌生并扩展直至贯通.在数值模型当中，裂纹主要产生在ITZ 区域以及加载方向的水泥砂浆中.不同试样由于骨料分布情况的不同，体现在混凝土拉伸破坏的峰值应力有一定的差别，最大为4.04 MPa，最小为3.09 MPa. 因此，即使在同一尺寸、同一配比的情况下，骨料的随机分布依然会对混凝土的破坏强度和破坏模式产生影响.

图8 0.01 m/s 加载速度下不同试样模型的应力应变曲线Fig. 8 Stress-strain curves of different specimen models under 0.01 m/s loading speed

2.2 裂纹空间演化过程

图9 为加载速度0.01 m/s 下混凝土试件不同应力水平下的破坏情况. 应力峰值60%之前，因加载位置处的应力集中现象以及骨料和水泥砂浆变形的不匹配，只在加载位置附近的骨料周围有少量裂纹产生；随着载荷的增加，达到应力峰值80%～90%时，骨料周围出现了较为集中的裂纹并进一步扩展；峰值载荷处，沿加载方向在试件径向产生较多的裂纹，裂纹连续贯通形成宏观破裂面，混凝土巴西圆盘试件发生破坏.

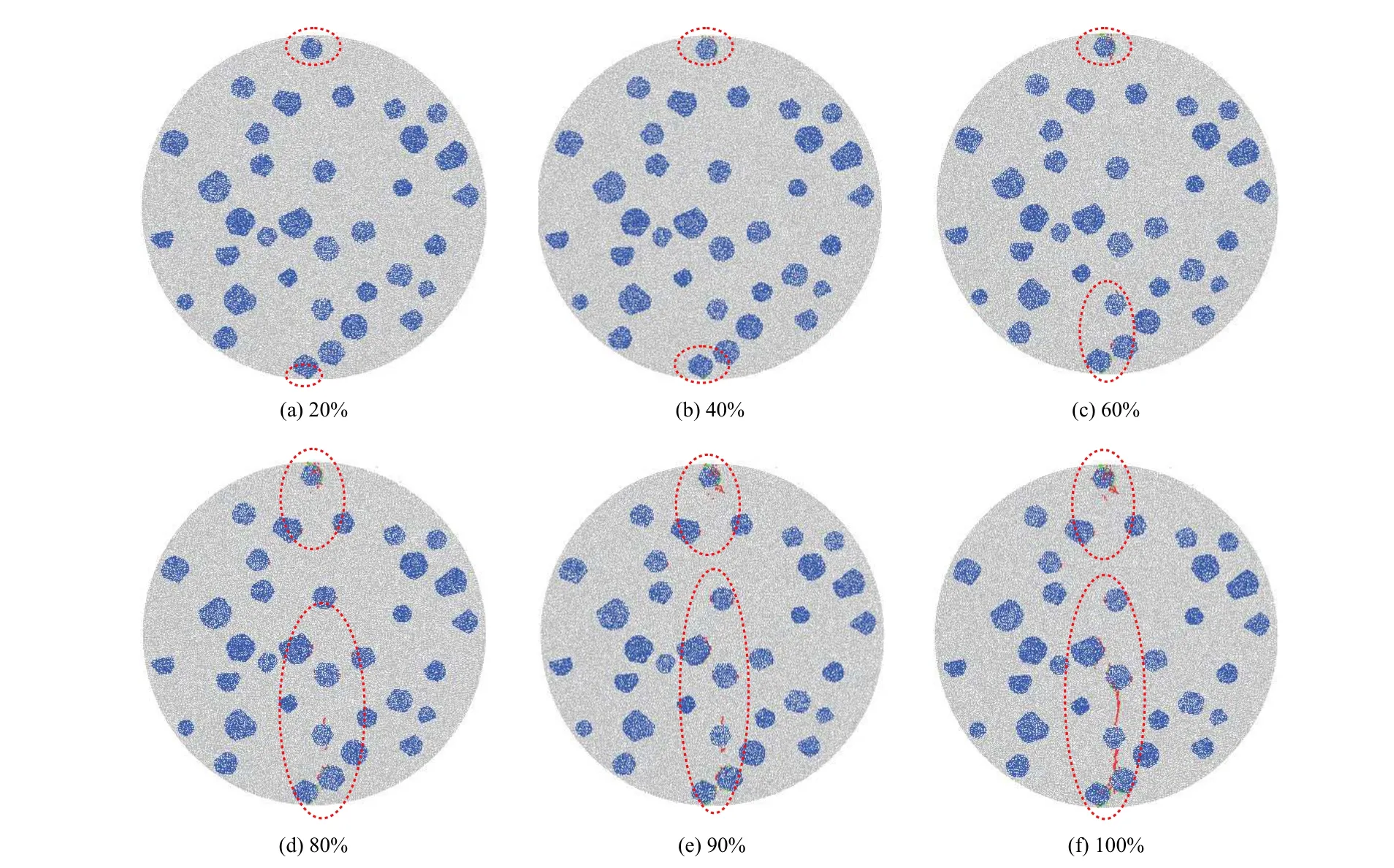
图9 0.01 m/s 加载速度下不同应力水平时裂纹发展情况Fig. 9 Crack development at different stress levels under 0.01 m/s loading speed

为研究加载速度对混凝土拉伸破坏的影响，设置加载速度为0.01 ，0.10 ，1.00 m/s，分别对混凝土试件的破坏进行数值模拟，混凝土巴西圆盘试样破坏的模态如图10. 破坏特征有：①在0.01 m/s 与0.10 m/s的加载速度下，沿加载方向的裂纹主要在水泥砂浆中扩展并绕过骨料，形成宏观裂纹贯穿整个混凝土圆盘；此外，加载位置处由于有应力集中而产生有大量裂纹，并伴随有少量的次生裂纹. ②加载速度增加到1.00 m/s 时，加载端产生了更多的裂纹，且整个圆盘上出现了多条贯穿裂纹以及大量的次生裂纹，试件呈现粉碎性破坏. ③对比3 组实验结果可以看出，加载速度越小，混凝土破坏越是呈现出一种沿加载向发生的劈裂破坏，裂纹沿着砂浆内部以及砂浆与骨料的界面扩展，与准静态加载下的失效模式非常相似；然而，在较高的加载速度下，更多的裂纹分布在整个试样中，呈现出网状图案，大量裂纹渗透到了强度比砂浆以及砂浆和骨料界面强度更高的骨料内部去，与实验观察结果非常吻合[17].

图10 不同加载速度下混凝土试件的拉伸断裂模态Fig. 10 Tensile fracture modes of concrete specimens under different loading speeds

FJM 模型主要由两种单元构成：黏结单元以及非黏结单元，当法向应力σmax大于拉应力σb时，界面单元断开，形成一条拉伸裂纹，界面黏结单元变成非黏结单元.当剪应力τmax大于剪切应力τC时，黏结因剪应力破坏，界面单元断开形成一条剪切裂纹，界面黏结单元变为非黏结单元，最终残余摩擦开始生效.对模拟计算过程中的裂纹进行统计，可以进一步获得混凝土破坏中的裂纹类型.图11 为3 组不同加载速度下混凝土试件内裂纹随时间变化的曲线.当加载速度为0.01 m/s 时，总裂纹数为3 185，拉伸型裂纹数为2 864，占比89.9%，剪切裂纹数为321，占比10.1%；当加载速度为0.10 m/s 时，总裂纹数为3 241，拉伸型裂纹数为2 898，占比89.4%，剪切裂纹数为343，占比10.6%，说明这两种加载速度下混凝土圆盘试件是以拉伸裂纹为主导的破坏；加载速度为1.00 m/s 时，总裂纹数约为10 000，拉伸型裂纹约为8 600，占总裂纹数的85%左右，剪切裂纹约为1 600，占比15%左右，裂纹数量大幅增加，但拉伸型裂纹占比降低.整体来看，随着加载速度的增大，裂纹数量也在增加，拉伸型破坏始终为混凝土试件的主要破坏模式.

图11 不同加载速度下混凝土破坏的裂纹演化Fig. 11 Crack evolution of concrete failure under different loading speeds

表2 给出了不同的加载速度下混凝土试样的抗拉强度. 从结果可以看出，抗拉强度随着加载速度的增大而提高，这一现象也证实了混凝土材料的抗拉强度存在着明显的应变率效应，且试样随着加载速度的增大，内部微裂纹产生和发展地更快，结构更快地发生拉伸断裂. 由于试验所测得的混凝土抗拉强度与试验方法、混凝土强度等级等直接相关，很多研究者得出的结论差别较大，且已有的研究中混凝土强度基本在C25 以下，而本文设计的混凝土强度为C40. 对比已有的研究结果[18]，强度为C20 的混凝土试件，应变率为10−2/s 和10−1/s 时相对于应变率为10−3/s 时的抗拉强度分别提高了2.8%和22%，本文模拟结果相应的增幅为1.4%和30%；且根据研究[19]，混凝土强度为C40 时，应变率为10−1/s 时抗拉强度约为4.9 MPa，故本文模拟结果基本符合真实试验规律.

表2 不同加载速度下混凝土的动态抗拉强度Tab. 2 Dynamic tensile strength of concrete under different loading speeds

3 结 论

本文通过建立混凝土巴西圆盘的颗粒流二维模型，对模型的细观力学参数进行标定，研究了混凝土骨料分布对混凝土断裂特性的影响；完整展现了巴西劈裂实验中混凝土从发生损伤到断裂的全过程以及其细观机理，同时，研究了加载速度对混凝土断裂特性的影响.结果表明：

①运用本文建立的混凝土二维颗粒流模型，可以成功实现对ITZ 及骨料断裂行为的数值模拟，这有助于对混凝土破坏模式及细观机理进行研究；混凝土巴西圆盘颗粒流二维模型随机骨料的分布对混凝土的破坏模式、峰值应力都会产生影响；

②在加载初期裂纹主要集中在混凝土试件加载位置处的骨料周围，剪切型裂纹多于拉伸型裂纹；当加载应力达到峰值应力的80%左右，裂纹开始集中产生并从加载端向中心扩展，随着加载应力的继续增大，裂纹连续贯通，混凝土最终发生脆性破坏；

③在加载速度较小的时候，试样裂纹模态比较单一，主要沿加载方向的砂浆及骨料界面贯穿试样整体；随着加载速度增大，次生裂纹增多，甚至可以呈现出网状图案，更多的裂纹渗透到了强度更高的骨料内部；在宏观层次上，混凝土试样的劈裂拉伸强度呈现出了应变率效应；

④混凝土试样宏观尺度的破坏在细观层次上主要有水泥砂浆和骨料内的拉伸型裂纹，以及水泥砂浆和ITZ 里的剪切型裂纹，拉伸型裂纹主导了混凝土试件的劈裂破坏.