Al/PTFE 活性材料弹丸冲击/爆燃行为数值模拟研究

肖建光，谢志渊，王岩鑫，王钊，聂政元

（1. 中北大学 机电工程学院，山西，太原 030051；2. 中国兵器工业第208 研究所 瞬态冲击技术国防科技重点实验室，北京 102202；3. 物华能源科技有限公司，陕西，西安 710061）

氟聚物基活性材料是一类新型含能复合材料，当其以一定速度碰撞目标时，既有良好的动能侵彻能力，又能在强冲击下发生非自持爆炸反应[1−3]，从而在动能侵彻和内爆两种毁伤机理的联合作用下，实现对目标的高效打击和毁伤，使弹药战斗部的终端毁伤效能获得大幅度提升[4−5]. 活性材料技术作为当前高效毁伤领域的热点研究方向之一，受到了世界各国的广泛关注和深入研究[6−11].

数值模拟在活性材料的毁伤效应研究中发挥着重要作用，选用合适的材料模型是确保数值模拟有效性的关键. 美国陆军研究实验室的RAFTENBERG等[12]对Al/PTFE 活性材料杆条的冲击变形行为进行了实验研究，标定了活性材料PSD 及Johnson-Cook模型参数模拟，分析了活性材料杆条碰撞金属靶板的变形行为，数值模拟结果与碰撞初期的实验结果吻合较好. 北京理工大学蒋建伟等[13]基于Voigt-Reuss-Hill 混合准则，通过理论计算得到了Al/PTFE的JWL 状态方程参数. 中北大学李玲琴[14]通过圆筒实验测定了低密度PTFE/Al 活性材料的JWL 状态方程参数，并推算出了密度为2 g/cm3的活性材料JWL状态方程参数. 北京理工大学王海福等[15]采用Shock状态方程和Johnson-Cook 强度模型模拟了活性材料引爆屏蔽装药的能力，得到了活性材料引爆屏蔽装药的临界速度. 张雪朋等[16]研究了活性药型罩聚能装药作用混凝土靶的毁伤效应，采用Powder Burn 模型模拟了活性材料的爆破行为.

从以上研究可见，由于缺乏一个有效、统一的材料模型，目前在模拟活性材料侵彻/爆燃行为时通常将整个过程分为惰性侵彻与化学爆破两个阶段，然后对两个阶段分别研究. 虽然美国莱特州立大学(Wright State University) 的ROSENCRANTZ[17]基于压力点火准则实现了活性材料侵彻与爆燃两个阶段的耦合研究，但与传统高能炸药显著不同，活性材料配方对其点火行为具有重要影响，传统压力点火准则难以适用于所有的活性材料配方. 然而，ROSENCRANTZ 并没有为点火准则及参数提供相应的调整接口，无法实现对不同配方活性材料的侵彻/爆燃行为的准确模拟. 在点火准则研究方面，美国海军水上作战中心（Naval Surface Warfare Center）MOCK 等[18−19]通过Taylor 撞击实验研究了密实活性材料的点火行为，发现该种材料的点火延迟现象与撞击压力、组分粒径等因素有关. 当撞击压力从0.78 GPa 提升至6.33 GPa时，点火时间从56 μs 缩短至4 μs. Al 粒径越大，点火时间越长、点火压力阈值也越高. 德州理工大学OSBORNE 等[20]采用持续加热的方式研究了Al/PTFE活性材料在惰性气体环境下的热分解问题，研究发现包含纳米级铝粉的活性材料在440 ℃附近发生了预点火反应，致使其点火感度和放热效应比微米级铝粉的活性材料均大幅度提高.

本文在前人研究的基础之上，针对活性材料撞击点火释能的特点，基于AUTODYN 软件材料模型的二次开发，通过增加参数可调的点火准则实现对活性材料侵彻/爆燃耦合行为的数值模拟，对揭示活性材料能量释放机理具有重要的意义.

1 数值模拟方法

1.1 活性材料冲击/爆燃一体化材料模型

采用冲击状态方程描述含能材料未反应时的压力状态：

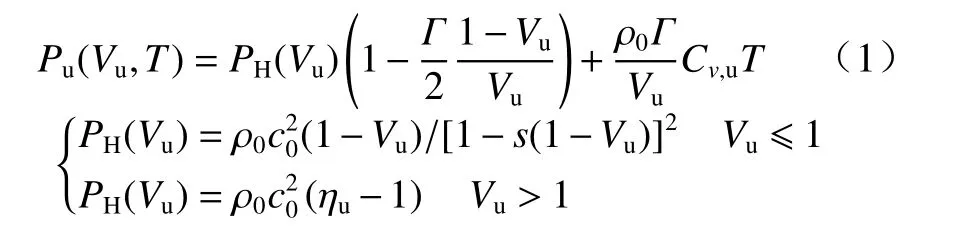
式中：下标u 表示含能材料未反应时的状态；V为相对体积；Γ为Gruneissen 系数；T为温度；ρ0,c0为材料初始密度与声速；Cv,u为比热；s为斜率.

采用JWL 方程[21]描述含能材料已反应时的压力状态：

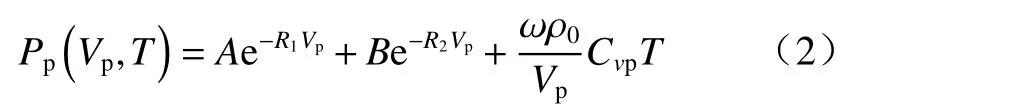
式中：下标p 表示含能材料已反应时的状态；V为相对体积；ρ0为密度；Cv、T分别为材料的比热容与温度；A、B、R1、R2、ω为常数.

在含能材料发生化学反应释能过程中，通过定义反应度F（F=0 代表未发生反应，F=1 代表完全反应）描述未反应材料与反应产物的混合物. 此时混合物的体积定义为

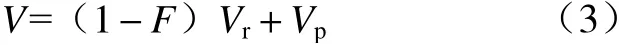
式中Vr、Vp为未反应与已反应含能材料的相对体积.

混合物反应速率即反应度对时间的导数为

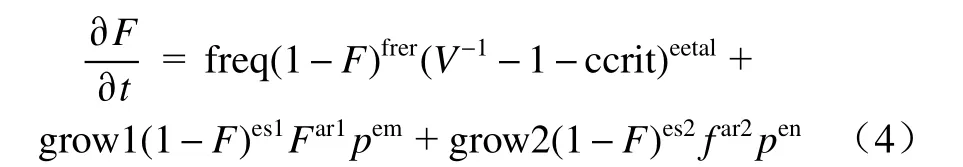
式中：p为压力；ccrit 为发生点火的最小压缩度，当压缩度小于ccrit 时不点火；freq 和eetal 为点火控制参量；frer、es1 和es2 为反应进行方向控制参数；grow1、ar1 和em 为点火后早期增长反应控制参数；grow2、ar2 和en 为高压反应控制参数[21].

反应速率分为点火、增长和完成三个物理阶段，通过相应参数调整可控制其反应速率. 活性材料撞击释能行为与传统炸药冲击起爆有一定相似性，但其也有自身的特点，如点火阈值变化范围大、反应速率慢、反应产物压力小等. MOCK 等[18−19]通过Taylor撞击实验研究了密实活性材料的点火行为，得到活性材料点火延迟时间随撞击压力的关系为

式中：t为点火延迟时间；σTS为发生点火需要的最小应力；a、b、c为与粒径有关的材料常数.

另一方面，如果活性材料在撞击或加热过程中的温度达到聚合物分解温度时，点火也将发生[20]. 综合上述分析，本文采用的点火准则为

式中Td为活性材料所含聚合物的分解温度.

由于在模型中添加了活性材料的点火准则，该方法可以解决当前主流有限元软件在模拟冲击爆炸问题时难以调整点火判据的问题，从而可以有效模拟活性材料侵彻/爆燃行为.

1.2 活性材料冲击/爆燃一体化材料模型二次开发

AUTODYN 是一款功能强大的显式有限元分析软件，软件自身含有丰富的材料库，并允许添加用户自定义材料模型. AUTODYN 软件为用户二次开发提供了AUTODYN user_subroutines 文件包，该文件包中的mdeos_user_1.f90、mdero_user_1.f90、mdfai_user_1.f90、mdstr_user_1.f90 文件分别对应材料的状态方程、侵蚀模型、失效模型及强度模型，用户需要在Visual Studio 软件中以FORTRAN 语言编写相应的子程序以满足不同的数值模拟需求.

通过编写mdeos_user_1.f90 子程序将活性材料冲击/爆燃一体化材料模型嵌入到AUTODYN 软件中，在编译生成后的AUTODYN 用户自定义程序中即可使用该材料模型. 此外，通过对usrsub2.f90 子程序的编写，实现了对活性材料实时整体反应度的提取.

2 数值模拟

2.1 计算模型

在AUTODYN-3D 平台上，针对网格畸变造成计算成本高的问题，采用SPH 算法进行建模. 为了进一步提高计算效率，采用1/2 对称模型进行模拟. 图1中双层间隔铝板的尺寸为Φ120 mm，第一层与第二层铝板厚度分别为2 mm 与4 mm，前后铝板之间的间距为200 mm. SPH 粒子间距为0.5 mm，计算共采用的粒子数约为130 000，所采用计算模型如图1 所示.

图1 活性材料弹丸撞击双层间隔铝板计算模型Fig. 1 The calculation model of the impact of the reactive material projectile on the double layer aluminum plate

2.2 模型参数

活性材料在高速碰撞过程中将产生大应变、高应变率和高温等特征. 采用Johnson-Cook 强度模型描述未反应态活性材料弹丸在高速撞击条件下的响应，该模型定义的材料屈服面为：

式中：εp为等效塑性应变：为归一化的等效塑性应变率；TH= (T-Troom)/(Tmelt-Troom)；A、B、C、N、m为材料常数.

当塑性变形较大时，材料将发生失效. 本文采用Johnson-Cook 失效模型描述活性材料的失效行为，该模型定义的失效应变与损伤因子为

式中：Δε等效塑性应变增量；εf为失效应变；σ*为归一化的等效塑性应力；D1～D5为材料常数. 由式(8)可知，当塑性应变为0 时，材料损伤为0；当损伤因子为1 时，材料完全破坏失效，此时材料只能承受压力而不能承受拉力或剪切力.

结合2.1 节中的状态方程、点火增长及点火准则模型，可实现对活性材料弹丸冲击/爆燃行为的数值模拟，模型主要参数见表1. 本文所采用的活性材料配方与文献[12 − 14]中采用的一致，因此未反应活性材料冲击状态方程与Johnson-Cook 强度模型参数取自文献[12]，已反应活性材料材料模型参数取自文献[13 − 14]. 2024 铝采用Shock 状态方程和Johnson-Cook 强度模型，其材料模型参数取自文献[22].

表1 活性材料冲击/爆燃一体化材料模型主要参数Tab. 1 Partial parameters of impact/deflagration materials model of reactive materials

3 活性材料弹丸撞击实验

3.1 试验设置

开展了PTFE/Al 活性材料弹丸高速撞击双层间隔铝板的试验. 试验测试系统如图2 所示，该系统主要由一级轻气炮、双层间隔铝靶、激光测速仪及高速摄像机等部分组成，弹丸速度由激光测速仪测量，弹靶作用过程由高速摄像机记录.

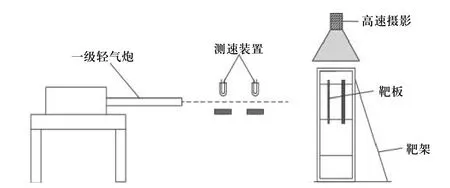
图2 实验方案Fig. 2 Schematic diagram of experimental setup

采用的圆柱形活性材料弹丸尺寸为Φ15.5 mm×15.5 mm 与Φ15.5 mm×7.75 mm，由零氧配比的聚四氟乙烯/铝（PTFE/Al）粉体经混合-冷压-烧结硬化等工艺制备而成，烧结后材料密度为2.27 g/cm3. 双层间隔铝板尺寸均为120 mm×120 mm，铝板厚度为前板2 mm/后板4 mm，两层铝板之间的间距为200 mm.

3.2 试验结果

采用高速摄像机记录了活性弹丸高速碰撞双层间隔铝板的冲击爆燃释能响应过程，拍摄的图片如图3 所示. 当撞击速度为293 m/s 时，活性弹丸在撞击前靶后产生了较为强烈的火光，说明此时部分活性材料已被激活并发生了爆燃反应. 撞击后火光强度持续增强，在262 μs 达到峰值（图3（b）），随后其强度逐渐衰减，说明活性弹丸整体反应速度经历了加速与减速两个典型阶段. 也就是说，在初始碰撞后随着时间的增加，达到点火阈值的活性材料越来越多，此时整体反应度的增加速度持续提高，即为加速阶段. 这种加速趋势直到262 μs 达到最大，然而随着时间的增加，达到点火阈值的活性材料反应趋于完全，此时由于第一次碰撞已结束因此没有更多的活性材料被激活，整体反应度的增加速度逐渐降低，即减速阶段. 从活性弹丸的形貌来看，其在撞击第一层靶后基本保持完整，并在其周围伴随有大小不一的碎片.从弹丸尾部明显的凹痕（图3（d））可以推测这些碎片应该是撞击时从弹丸表面脱落的. 当撞击第二层靶板后，活性材料产生了更为持久的火光，该火光在1 419 μs时达到最强，直至2 522 μs 时才逐渐消逝. 从图3（f）中可以看出，活性弹丸在293 m/s 撞击速度条件下并未完全反应，仍有大块的活性破片并未被激活，说明在当前试验条件下活性材料很难产生自持的爆燃反应. 此外，从活性弹丸在撞击第一层靶与第二层靶后的质量损失可以看出，活性材料在撞击第二层靶后产生更多的爆燃反应，释放了更多的化学能.

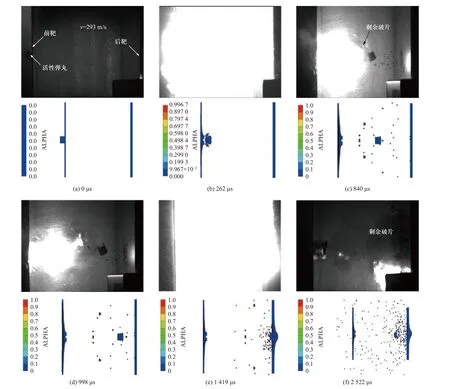
图3 活性材料弹丸冲击爆燃释能过程（速度v=293 m/s）Fig. 3 The process of impact/energy release by reactive materials projectile (impact velocity v=293 m/s)

当撞击速度提高至650 m/s 时，爆燃反应同样发生于撞击前后靶板时的两个典型阶段，其主要区别有两个方面. 一是活性弹丸在撞击第一层靶后最强火光出现的时刻较低速时提前了约52 μs. 这是因为更高的速度将产生更大的压力与应力. 尽管更高的应力可能使更多的活性材料激活并发生爆燃反应，在一定程度上可以延长反应时间. 然而由式（3）可知，爆燃反应速率随着压力的提高而提高，也就是说，反应速率的提高是最强火光出现时刻提前的决定性因素. 二是活性弹丸在撞击第二层靶后的爆燃时间增加了，低速时爆燃反应在2 522 μs 内基本结束，而高速时爆燃反应的结束时间延长至5 173 μs. 这主要是因为在撞击速度提高以后，剩余活性破片撞击第二层靶的速度也提高了，导致更多的活性材料被激活并发生了爆燃反应. 事实上，这些活性材料并不是同一时刻被激活的，在碰撞局部区域和碰撞产生的碎片云周围存在燃烧波的传播，燃烧波的传播时间可能是导致活性弹丸在撞击第二层靶后燃烧时间长的主要因素. 此外，从图4（c）和4（d）中可以看出，当穿透第一层靶板后，活性弹丸尾部也发生了明显的爆燃反应，该反应是撞击压缩波在弹丸尾部自由面反射形成的拉伸波诱发的，因为拉伸波可以使弹丸尾部的材料产生裂纹，而材料在断裂前必然经历了足够的塑性变形，其产生的塑性功可以为活性材料的激活行为提供足够的能量.

图4 活性材料弹丸冲击爆燃释能过程（速度v=650 m/s）Fig. 4 The process of impact/energy release by reactive materials projectile (impact velocity v=650 m/s)

爆燃反应产生的火焰外观、强度、大小等特征，本质上与活性材料弹丸的点火和反应比例密切相关.由于火光屏蔽作用和当前测试方法的不足，研究活性材料弹丸在高速碰撞过程中的点火及相关机理极为困难. 因此，本文基于AUTODYN 软件编写了点火阈值可调的材料模型，实现了对活性材料弹丸冲击诱发爆燃行为的数值模拟. 活性材料弹丸的点火行为、实时反应比例与反应温度在下文进行详细讨论.

4 讨 论

4.1 活性材料弹丸点火行为

图5 与图6 给出了活性材料在撞击后200 μs 的典型点火过程. 当以293 m/s 的速度冲击平板时，在活性弹丸和铝板边缘之间的最强剪切区最先发生着火（图5（c））. 尽管活性弹丸前部在撞击中承受了最大的压力，但是活性弹丸的前部未能被点燃，这一现象证实了活性材料的点火主要由剪切应力而不仅仅由撞击压力诱发. 事实上，剪切应力会造成微观上Al 粒子与PTFE 基体界面的相对运动，在该过程中摩擦、分子间相互作用等因素将造成界面温度升高，达到温度点火阈值后Al/PTFE 活性材料即可产生化学反应. 当冲击速度提高到650 m/s 时，活性材料与靶板侵孔表面的剪切作用更为明显，导致二者接触面上更多的活性材料被激活（图6（c））.

图5 活性弹丸点火过程（速度v=293 m/s）Fig. 5 The ignition process by reactive materials projectile (impact velocity v=293 m/s)

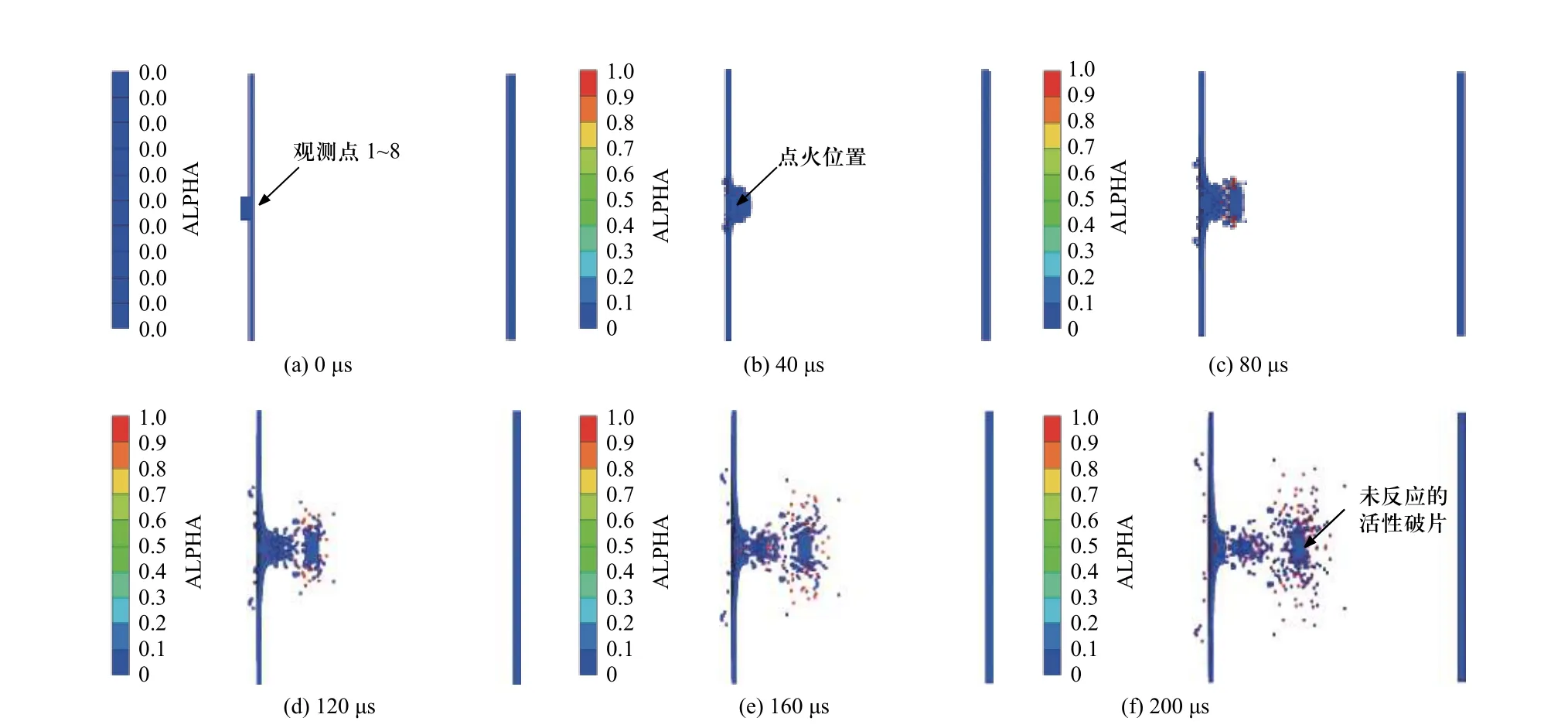
图6 活性弹丸点火过程（速度v=650 m/s）Fig. 6 The ignition process by reactive materials projectile (impact velocity v=650 m/s)

通过在活性弹丸前表面设置观测点获得了典型位置处点火常数、反应度、压力和温度随时间的变化曲线，如图7 所示. 撞击后首先在撞击接触面产生高压脉冲，由于本文采用等效塑性应力与时间的乘积作为判断点火的条件，当撞击速度为293 m/s 时撞击接触面上的材料并未被立即激活. 事实上，等效塑性应力的计算在AUTODYN 中包含两部分：状态方程计算的流体静压力和本构模型计算的偏应力. 虽然压力很高，但点火指数并未明显提高，撞击瞬间并没有产生点火所需的阈值应力. 在此之后，向前传播的压缩波被前靶板背部的自由表面反射，产生与活性弹丸运动方向相反的稀疏波，导致材料的压力急剧下降. 稀疏波还可以增强颗粒在活性弹丸中的速度变化，这有利于在活性材料中产生高应力. 之后，点火指数线性增加到用户设定的值（本研究将该值设置为1），此时活性材料被激活发生爆燃反应，爆燃释放出大量的化学能以压力势能和内能的形式存在，基于压力和温度平衡条件可以计算获得未反应活性材料与爆燃产物混合物的压力. 随着反应度ALPHA 的增加，压力和温度显著提升. 如图7 所示，当ALPHA 增加到1 时，说明此时爆燃反应结束，粒子的压力和温度趋于平稳.

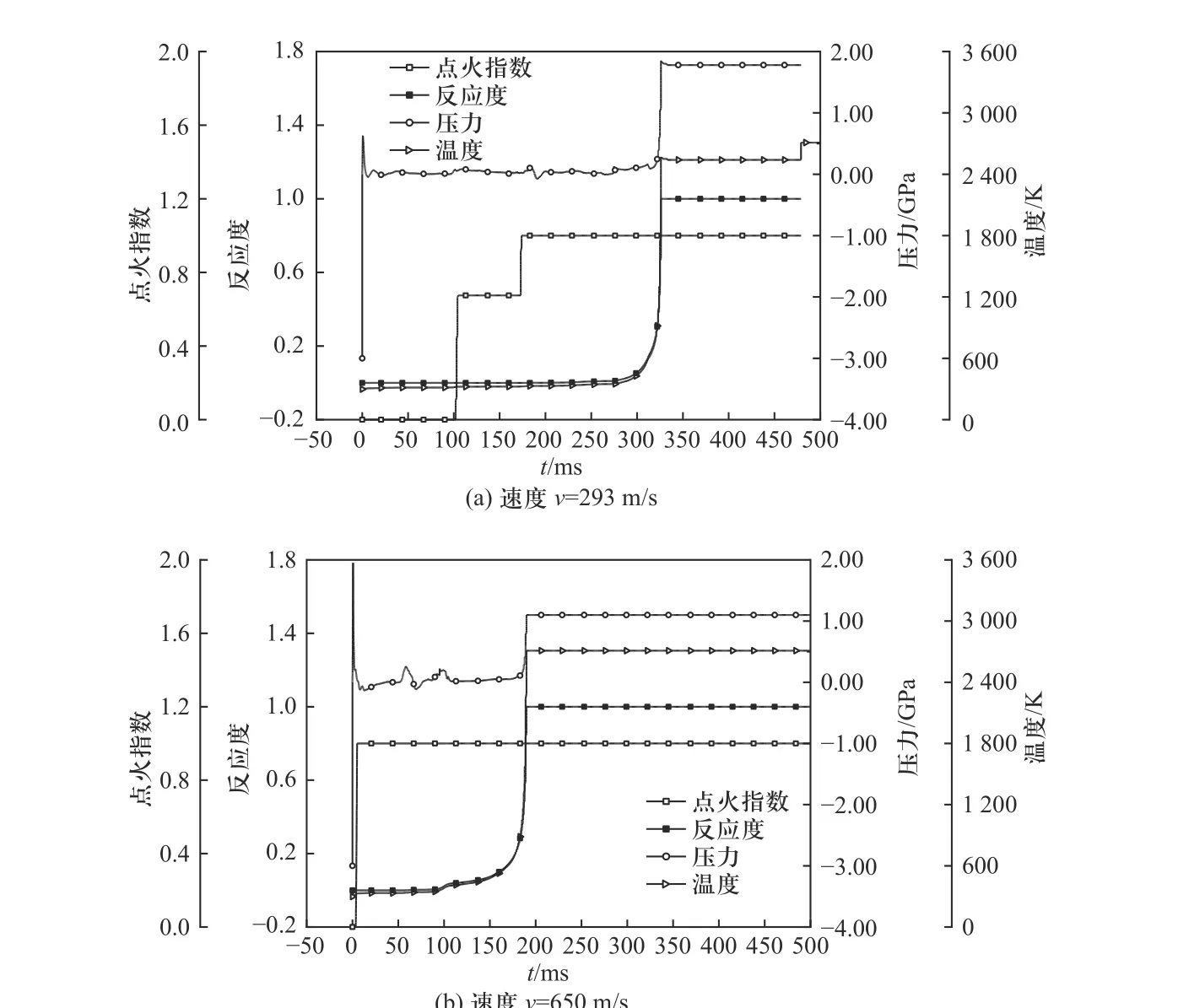
图7 活性点火机理分析Fig. 7 The ignition mechanisms

4.2 活性材料能量释放行为

4.2.1 反应度

为了得到侵彻爆燃过程中活性弹丸实时的整体反应度，编写了一个在每个计算循环结束时执行的子程序. 定义活性弹丸的整体反应度为

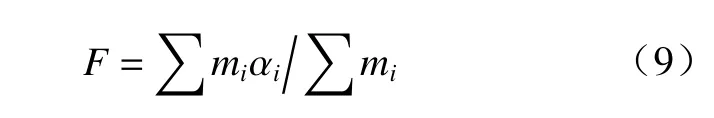
式中：mi为活性弹丸中包含的每个粒子质量；αi为相应粒子的反应度.

碰撞速度分别为293，650 m/s 时活性材料弹丸整体反应度随时间的变化曲线如图8 所示. 从图中可见，在穿透前板后活性弹丸的整体反应度显著提高，如前文所述，当点火指数达到预设值时，部分活性材料开始发生爆燃反应. 在撞击第2 层铝板之前，活性材料整体反应度持续增加，造成这一现象的原因可从两个方面进行考虑：一是被激活的活性材料完成彻底的爆燃反应需要一定的时间，二是因为已反应的活性材料释放出大量的热能形成高温区，热量将向低温未反应的活性材料转移，导致周围未反应活性材料温度迅速升高至点火温度，进而持续地释放化学能. 随后反应度曲线形成了一个拐点，对应于剩余活性侵彻体高速撞击第2 层铝板的时刻（540，1 049 μs），之后活性材料反应度以更快的速度增加，意味着活性材料弹丸在撞击第2 层靶板时反生了更为剧烈的爆燃释能现象. 尽管如此，在当前撞击速度条件下，活性材料弹丸的化学能不足以得到完全释放. 当速度从293 m/s 提高至650 m/s时，活性材料弹丸整体反应度由0.079 提升至0.224，数值模拟结果与试验基本一致，因为从高速摄影和回收后的碎片都观测到了大量未反应的活性材料.

图8 活性材料弹丸整体反应度随时间的变化曲线Fig. 8 The overall reaction ratio of RMP versus time

4.2.2 温度效应

根据热力学第一定律，爆燃反应释放的丰富化学能将转化为爆燃产物的压力势能和内能. 高压将使爆燃产物迅速膨胀，而内能会使产物温度升高. 图9为活性材料剩余侵彻体撞击第二层铝板时的温度分布. 当撞击速度分别为293 ，650 m/s 时，粒子达到的最高温度分别为2 606，2 780 K. 这个温度与参考文献[23]中红外分幅机和瞬态高温计（1 600～2 800 K）捕获的结果一致. 瞬态高温计测试的理论基础是黑体辐射定律，测得的温度其实就是爆燃产物的温度，即粒子的温度. 在撞击过程中活性材料发生的化学反应为：

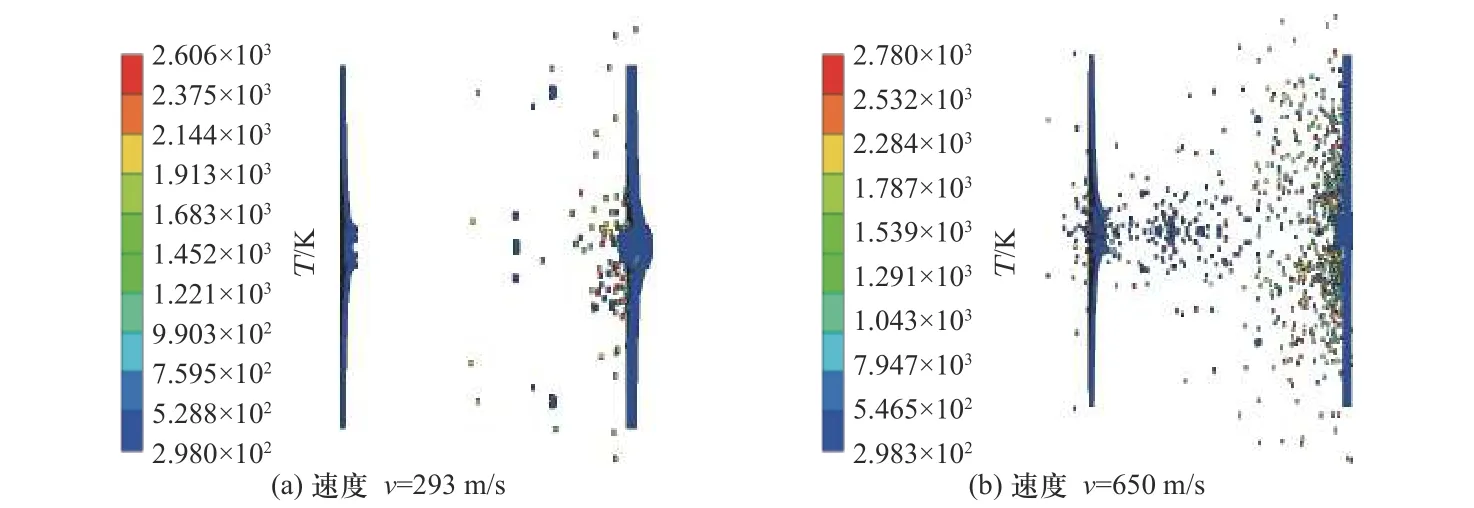
图9 撞击后板处的温度分布Fig. 9 The temperature distribution at the impact on the rear plate

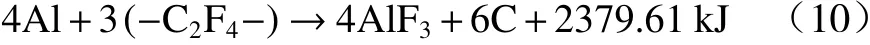
假设释放的化学能完全转化为爆燃产物的内能，则可以根据爆燃产物的比热容来估计温度. 取AlF3和C 的比热容为100.831，21.609 J/(mol·K)，可得爆燃产物的温度约为4 464 K. 数值模拟结果比理论计算结果偏低，这是因为活性材料释放的化学能有一部分转换为爆轰产物的压力势能，在侵彻靶板过程中高压粒子膨胀做功最终转换为靶板的破坏能. 从图中还可以看出，并不是所有粒子都达到了最高温度，这是由于粒子在撞击过程中或撞击后持续膨胀，使得粒子对外界做功进而导致其自身内能下降的缘故.

5 结 论

①基于AUTODYN 软件的二次开发功能，编写了适用于活性材料的状态方程、点火模型及整体反应度计算子程序，实现了对活性材料弹丸高速侵彻双层间隔铝板冲击释能过程的数值模拟.

②当活性材料弹丸速度较高时，撞击压缩波在弹丸尾部自由面反射形成的拉伸波可以使尾部活性材料经历足够的塑性变形而发生点火释能.

③通过数值模拟获得的活性弹丸整体反应度与试验中产生的火光强度变化趋势一致，得到的温度与理论分析及相关文献中报道的结果也基本一致，说明本文采用的数值模拟方法具有较高的可信度，可为活性材料弹丸在高速撞击过程中冲击/爆燃释能的定量分析提供一种重要的研究手段.