声信号特征融合的变压器故障判断方法

杨光辉，杨光粲，黎宏锐

（北京科技大学 机械工程学院，北京 100083）

变压器故障主要为机械故障、电气故障、变压器过热等，机械故障是导致后者故障的主要原因[1].机械故障诊断中，特征提取是核心[2]. 故对变压器故障提前检测、防止事故发生有重大意义.

变压器的诊断方法有特征气体法、神经网络法、支持向量机法、振动分析法等，如SHERIF 等[3]利用气体特征检测的变压器早期故障. WANG 等[4]将振动传感器贴在变压器外壳，通过获得振动信号，提取特征信息，进而对变压器的机械故障施行检测分析；赵莉华等[5]提取变压器振动信号特征量，利用SVM验证处理得到特征量的故障识别效果. 一方面，变压器的故障噪声种类繁多，难以获得大量的故障样本，使得神经网络、向量机等无法成功运用在变压器可听声故障诊断中；另一方面，振动信号获取属于接触式测量，测量传感器需贴合在变压器上，存在难以带电更换的安全问题，具有一定的局限性. 由于振动与声音的信号来源同为故障点的位置，且声波具有衍射和散射特性，采用声音检测无需接触测量，可解决振动传感器的布置问题[6].

可听声检测具有无电连接、精度高、无需接触、无损检测的特点，使它成为变压器故障检测的热点.变压器的不同故障也会产生不同声信号，侯温良[7]利用频谱相关系数法对机器正常与异常声信号进行比较，从而诊断故障. 赵书涛等[8]基于声波分析法设计了基于声波识别的电气设备故障诊断专家系统的总体方案.但时频分析具有一定的局限性，例如小波基难以选择等问题，影响故障检测的准确性，仍待深入研究.

人类听觉对声音信号的识别非常敏感，抗干扰能力强，倒谱域来源对语音的处理，从倒谱域中提取的特征符合人的实际感受，其中对语音信号的特征提取常见的有梅尔频率倒谱系数(MFCC)特征提取及线性预测倒谱系数(LPCC)特征提取. 王丰华等[9]对变压器噪声信号进行分帧加窗处理，综合运用加权处理法和主成分分析法对现有的MFCC 特征提取算法进行改进，进而基于VQ 算法对变压器噪声信号进行识别. 基于倒谱域的特性，考虑变压器声音信号与人耳听觉信号的相似性，故引入倒谱域进行声音信号特征提取. 变压器产生的声信号由多物理场形成，单一的时频域、倒谱域等特征难以准确表达，故提取声信号不同角度的特征信息. 故障诊断技术很大程度上依赖于庞大的故障集，变压器声学故障集的真实样本较为稀缺，故障样本的不足导致目前基于声学的变压器故障诊断技术无法得到较大的提升；同时目前变压器声学检测依赖云平台，时效性较差.

针对以上问题，本文提出了一种声信号特征融合的变压器故障判断新方法，首先对声音信号进行分帧，提取信号在时域等空间域中不同角度的特征值，使用最大相关−最小冗余算法筛选出与正常变压器声信号最相关的特征集，最后对特征集进行加权熵主成分融合，降维后获取一维融合指标，减小了故障判断的计算量，提高检测的时效性. 以某变电站220 kV 与110 kV 变压器正常声音信号与故障仿真信号做计算实验，验证了算法的有效性.

1 可听声信号特征提取

1.1 变压器可听声信号预处理

正常变压器噪声持续、稳定，将变压器正常声信号作为平稳随机过程进行分析. 由于平稳随机过程的统计性不随时间的推移而变化，为了减轻数据计算量，故对声信号进行分帧，每帧信号互不影响，每帧时长设定为1 s.

1.2 变压器声信号特征提取

对采集到的变压器声信号分帧处理，在频域、时域、倒谱域、小波包域中依次提取特征.

1.2.1 频域特征提取

正常变压器产生的声信号频率范围一般在0～700 Hz 范围内，能量基本集中在100 Hz 的倍频处，50 Hz 奇数倍频处的能量较小[10]. 通过关注这些特殊频率处的能量分布可检测变压器信号变化.

通过高频能量比重、奇偶次谐波比等特征值可以对变压器声信号进行故障判断. 变压器声信号故障往往伴随着高频能量的变化，如电火花引起的声信号频率能量集中在1 000 Hz 频率以上. 考虑0～2 000 Hz范围内的频率能量，获得高频能量比重.

1.2.2 时域特征提取

时域信号最为直观，信号的波动与变化趋势在时域中进行体现. 从峭度指标、歪度、裕度指标、峰值指标等特征中找到有效表征变压器的时域特征.

1.2.3 倒谱域特征提取

MFCC 系数是基于人耳听觉理论而提出，Mel 频率域的转换公式为[11]

人类对1 000 Hz 以上的声音频率感知并不是线性分布的，需要将实际频率尺度转化为梅尔的线性频率尺度，便于对信号进行梅尔滤波. 归一化的梅尔滤波器组如图1 所示.

图1 Mel 滤波器组频率响应曲线Fig. 1 Frequency response curves of Mel filter banks

单帧声信号提取MFCC 特征只能体现自身静态的信息，丢失了帧与帧信号间的动态信息. 在原有的MFCC 静态特征中再加入动态差分系数提高识别效率.

线性预测倒谱系数是根据声道模型建立的. 通过获取线性预测系数(LPC)，再进行相应的倒谱系数提取可得到LPCC：

1.2.4 小波包域特征提取

利用小波包分解将变压器声信号的近似特征与细节特征进行提取，获取到对应频段的能量信息. 对信号利用db20 小波进行分解，获取能量谱.

2 特征融合与总体方案

2.1 最优特征集的选择

在变压器声信号特征提取后，对这些特征进行筛选，得到与正常变压器最相关的特征，同时特征间冗余较小. 利用基于互信息的最大相关−最小冗余法可以实现这一要求.

2.1.1 互信息

2.1.2 基于互信息的特征选择

基于文献[14]的mRMR 算法，对不同空间域中的特征进行筛选，从中过滤出有效表征变压器状态的特征. 训练集以正常声信号为正样本，以含有异常声响（含背景噪声和部分模拟的故障声响）的变压器声信号为负样本. 具体操作过程如下：

①将每帧得到的特征值与样本标签放入同一矩阵中，得到的变压器特征状态矩阵.

②矩阵标准化处理与网格划分. 由于各特征量纲不同，需要对变压器特征状态矩阵进行标准化处理，计算互信息需要获取到各特征随机变量的概率分布，因此，需要对各标准化后的特征进行网格划分. 通过大量的试验，选择网格数50 作为划分标准.

③利用式(5)分别计算两个随机变量的熵值及它们的联合熵. 计算特征间的互信息，同时计算特征与标签列的互信息，最终，得到互信息上三角阵矩阵.

2.2 特征融合

利用基于加权熵主成分的特征融合算法对变压器的特征集进行特征融合. 具体操作过程如下：

②计算Ⅲ级指标的加权信息熵. 每一个域至多有一个Ⅲ级指标矩阵，对Ⅲ级指标矩阵进行归一化

2.3 故障判断区间

2.3.1 融合指标置信区间估计

2.3.2 泊松过程的故障判断

变压器周围总会出现影响融合指标判断的因素，但这些并不是故障因素，容易引起系统误判. 将出现这一事件的随机过程视为泊松过程，为了检测方便，考虑出现这些事件的时间间隔. 由图2 所示，T1为故障时间区间，T2时间段为泊松总区间. 计算T1、T2时间段的步骤如下：

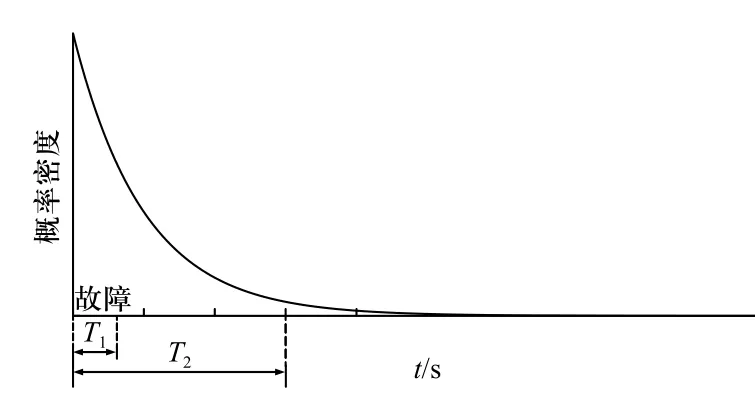
图2 概率密度故障判断Fig. 2 Probability density fault determination

在T1时间间隔内的点视为故障点，同时本文只考虑落在T2泊松总区间内的点，超出范围的时间间隔视为正常情况处理，不作为可疑点.

2.4 总体方案

利用变压器声音信号进行故障判断，首先对变压器声信号进行特征集获取，筛选出有效表征正常声信号的特征，对特征集进行融合得到一维融合指标，对融合指标构建置信区间. 系统需要实时监测变压器融合指标，通过对变压器声信号的实时采集，将信号转化为融合指标，进行区间判断；对落在泊松故障区间内的点视为故障点；并采取周期间隔式的巡检模式，即当一个周期结束时，对这段时间内采集到的所有点进行结算，故障率达到80%，视为故障发生，此时报警，否则重新循环检测. 总体方案分为训练与故障判断两部分，如图3、4 所示.

图3 声信号特征融合训练流程图Fig. 3 Flow chart of training of acoustic signal fusion

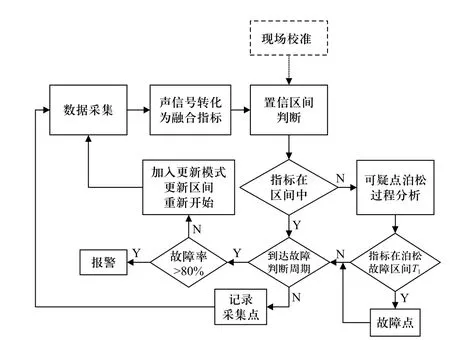
图4 故障判断阶段流程图Fig. 4 Flow chart of fault judgment

3 融合指标实验分析

变压器声音信号在正面中心附近保留较完整，将GRAS 40PP 声音传感器安置在变压器无风扇两侧各一个，均距变压器表面20 cm，离地高度160 cm. 采集时间为2019 年8 月22 日下午3:20−8 月23 日上午9:50，采样频率为51 200 Hz. 以某变电站220 kV 变压器A、B，110 kV 变压器C 作为采集对象，将采集到的部分正常变压器声信号与含有异响声信号作为训练集，其中异响声信号包含：背景噪声信号和仿真故障声信号. 同时将剩余数据作为样本集. 表1 为筛选出的20 个特征.

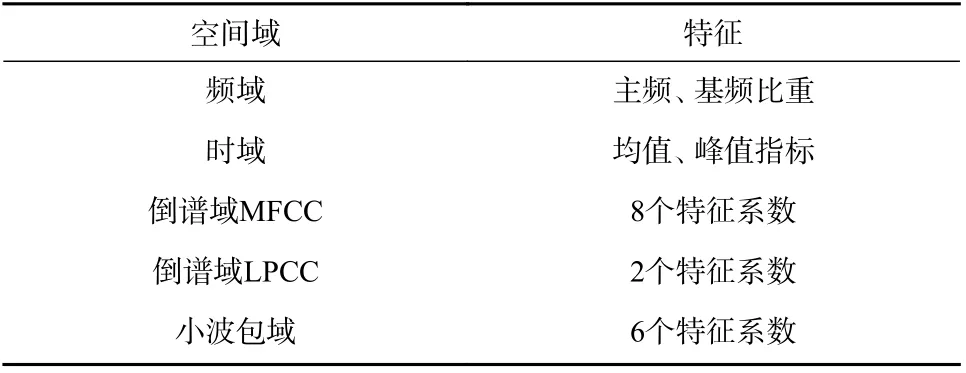
表1 筛选的特征集Tab. 1 Filtered feature set

利用加权熵主成分法对特征进行融合，获取到各域的权值如表2. 进行主成分分析，最后得到融合指标.考虑到一些域特征太多，以区间的形式表示权值范围.

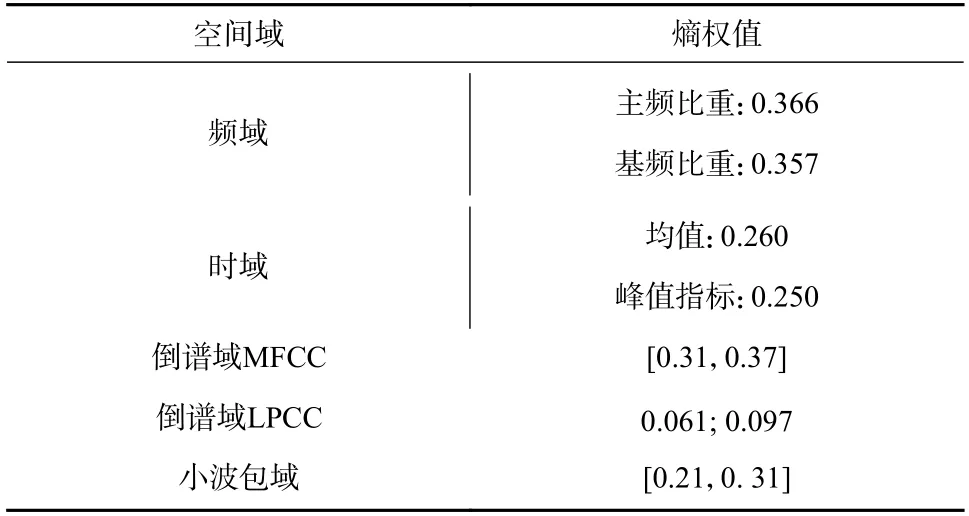
表2 各特征的熵权值Tab. 2 Entropy weight of each feature

3.1 正常声信号变压器融合指标

以变压器A 的负载情况为例，从0−10 点左右，变压器负载较低，而12−22 点处于用电高峰期，此时负载较大. 因此，可以将负载的变化基本分为高低两种情况进行考虑，在上午与下午分别采集到变压器高低负载下的声信号，获取融合指标.

获取变压器A、B、C 的高、低负载测试样本声信号，提取出它们的融合指标，每个站提取高、低负载融合指标各3 000 点，绘制融合指标图5，由图可知，高低负载对融合指标影响较小，A、B 变压器的融合数据基本维持在−0.1 附近，但变压器C 融合数据与其他站差异较大，维持在−0.35，主要原因在于变压器C 属于110 kV 等级，产生的噪声相对与220 kV 的变压器“嗡嗡”噪声较低.

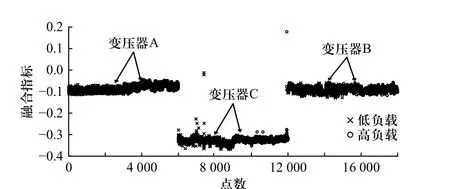
图5 高低负载下变压器融合指标图Fig. 5 Fusion index of power transformers under high and low loads

由融合指标实验分析表明，单一变压器的负载变化对融合指标的影响较小，达到了预期目标效果，验证了融合指标方法的准确性，但电压等级对融合指标影响较大.

3.2 背景噪声变压器融合指标

融合指标需要具有一定的鲁棒性，在变压器正常工作时，无法避免背景噪声的干扰. 对背景噪声进行采样，将它们混入正常变压器噪声中，获得背景噪声下变压器噪声融合指标. 图6～8 分别为采集到的雨天背景噪声、晴天背景噪声、风机背景噪声. 将背景噪声进行分帧，加入到正常变压器声信号中.

图6 雨天背景噪声Fig. 6 Rainy background noise

图7 晴天背景噪声Fig. 7 Sunny background noise

图8 风机背景噪声Fig. 8 Fan background noise

变压器声音信号加入背景噪声后，得到融合指标图9. 包括1 500 个正常220 kV 指标，300 个雨天干扰（打雷、车鸣、鸟叫、刮风等）指标，600 个晴天干扰（锤子敲击、车鸣、鸟叫、刮风等）指标，300 个风机干扰指标. 由图可知，背景干扰下的变压器声信号与原始声信号的融合指标存在一定的差异，但两者的区分度不明显，为了减小误判率，需要对含有背景干扰的融合指标进行归类，利用聚类分析对不同的背景噪声融合指标进行分类，构造置信区间.

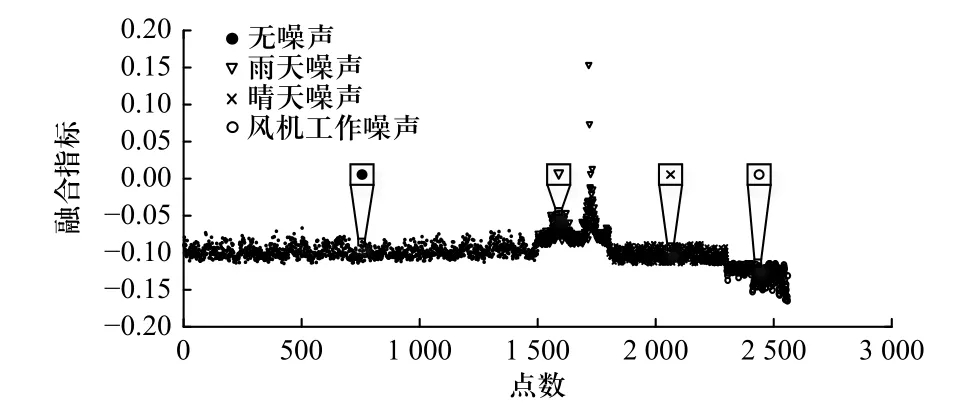
图9 背景噪声下融合指标图Fig. 9 Fusion index under background noise

3.3 故障噪声变压器融合指标

3.3.1 变压器绕组故障仿真声信号

运用comsol 多物理场仿真软件对220 kV 变压器下的绕组故障声信号进行仿真，得到绕组故障声信号. 图10(a)～10(c)分别表示绕组变形、绕组松动、绕组绝缘破损声信号.

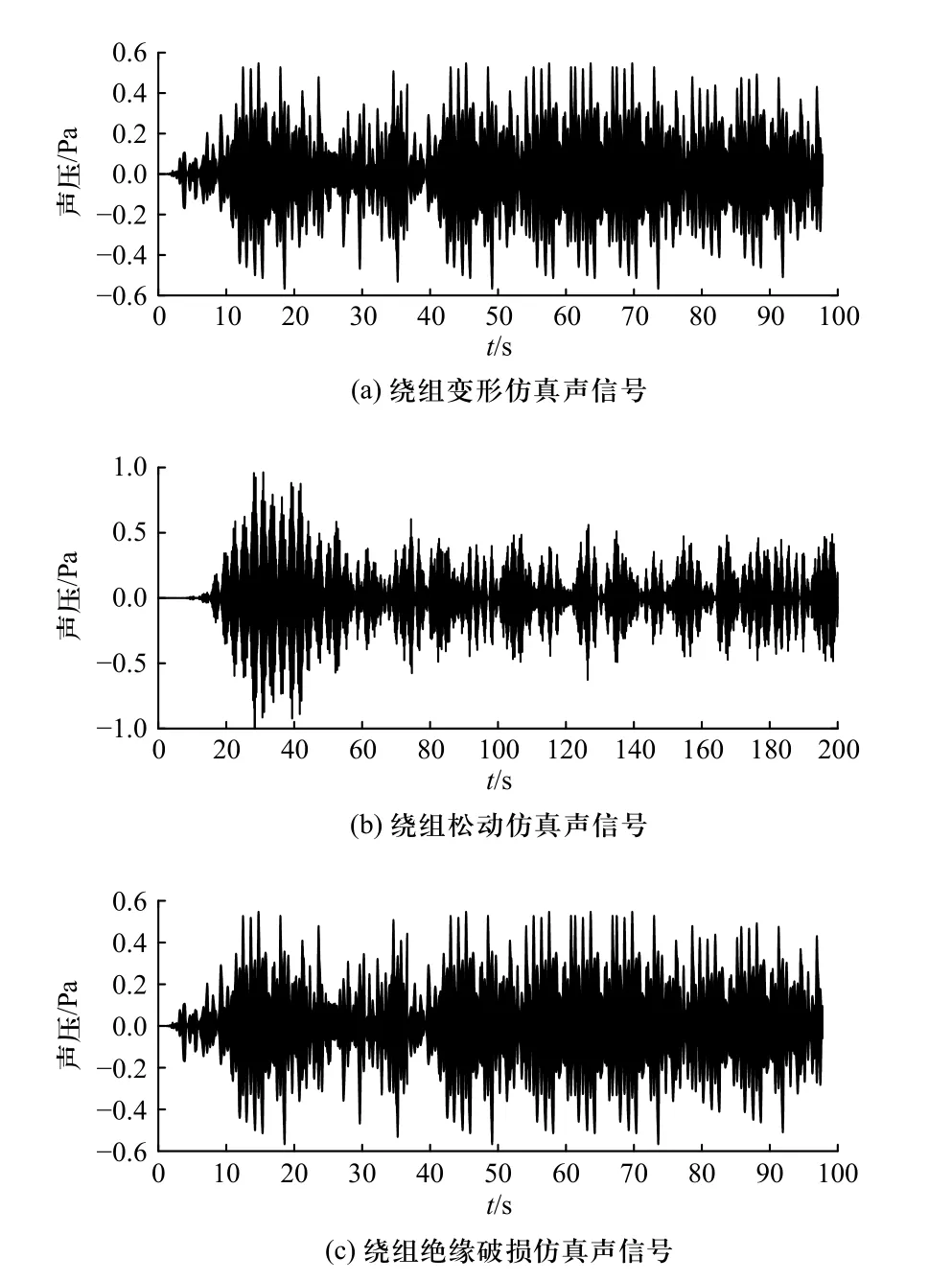
图10 仿真220 kV 变压器绕组故障声信号Fig. 10 Acoustic signal of winding fault of simulate 220 kV transformer

3.3.2 变压器仿真故障的融合指标

本文仿真了220 kV 变压器下的绕组故障，为了验证算法的可行性，获取这些信号的融合指标进行分析. 图11 可知基于仿真与模拟故障声信号的融合指标与正常情况下的变压器融合指标区分明显，表明基于声信号融合指标的故障判断方法具有一定的可行性.

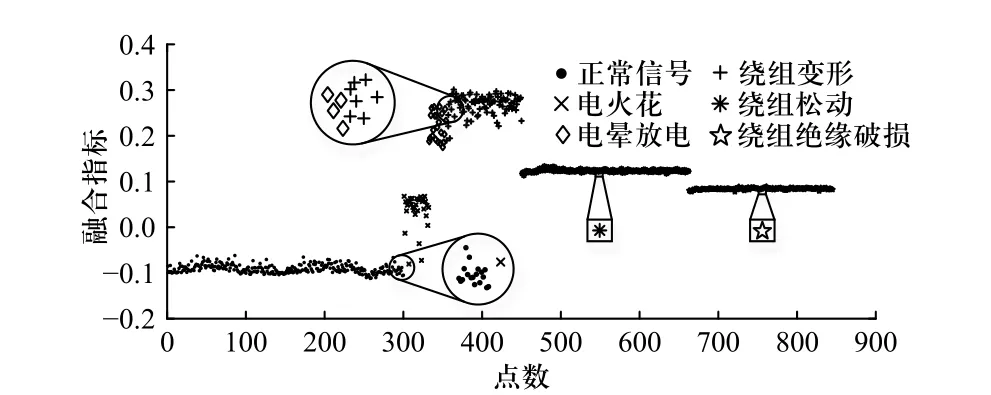
图11 220 kV 变压器仿真故障融合指标图Fig. 11 Fault fusion index of 220 kV transformer simulation

3.3.3 变压器检测算法对比实验

为了进一步说明所提出的算法对变压器故障检测的有效性，并考虑不同故障状态下的检测状况，分别与频谱相关系数法和声波分析法做出对比实验.频谱相关系数正常信号对相同故障信号分析结果如表3 所示.

表3 故障频谱相关系数Tab. 3 Fault spectral correlation coefficient

由于数据的差异性不大，故只列出经过大量实验稳定的数值，可以看出绕组故障类型稳定在0.24～0.27，电火花与电晕稳定在0.65～0.75. 由频谱相关系数法结论所知，故障与正常之间的频谱相关系数稳定在约0.1，故障与故障之间的系数稳定在约0.6，正常信号与正常信号的系数稳定在约0.9，范围因数据的差异所不同. 故频谱相关系数法能够检测出绕组产生的故障，而对于电火花和电弧故障检测则不准确，得出的结果容易误判为不同机器故障之间的谱相关系数. 这是因为电火花与电晕声信号自身较微弱，谱相关系数法比较考虑全局状况，不宜检测出一些瞬间故障，故此方法不适用于检测电火花与电晕故障.

声波信号分析法是基于小波包提取声信号的特征. 识别故障信号将其与正常信号分离，分解与重构信号. 此方法存在小波基难以精确选择的问题，不同小波基得到的结果也有不同，这就导致了故障提取模型的多变性，不能广泛适应变压器出现的多种故障问题.本文对5 种故障类型分别做了大量实验，因差异性不大，每组分别取均值得到5 种故障的特征向量，如图12 所示.

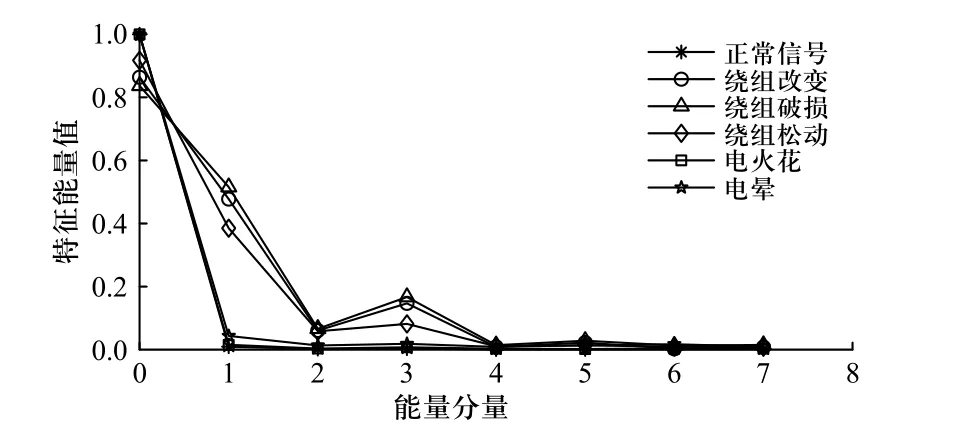
图12 小波包提取特征向量Fig. 12 Wavelet packet extracted feature vector

图12 所示为3 层小波分解重构的特征向量T=[E0E1···E7]，其元素为各频带的能量，横坐标为低频到高频的8 个频率成分信号特征能量分量k，k=0,1,···,7，纵坐标为归一化后的特征能量值Ek/E.由图12 所知，绕组故障与正常特征向量在低频段区分度较大，但在高频能量范围与正常信号较相似.而电火花与电晕则难以与正常信号区分，导致检测效果略差，且故障与故障之间差别较小，难以区分故障类型.

对比上述两种算法，本文提出的特征融合检测算法能够区分开故障类型，精确检测出变压器出现的故障，显著提升了变压器声音故障的检测效果.

3.4 声学特征融合故障判断

为验证变压器在正常工作中出现故障时及时检测，制作由正常数据与异响数据组成的连续声信号模拟现场环境输入系统. 该信号表示变压器由正常运行中到出现异响的30 min，具体组成为前10 min是现场采集到的变压器正常声信号；中间10 min 是在采集到的正常声信号中加入了风机等噪声声音，因现场常会存在这样的噪声信号干扰；最后10 min为正常声信号加入故障仿真声信号. 将该信号输入到声学特征融合故障判断系统，得到融合指标-时间曲线图，如图13 所示.

图13 融合指标-时间曲线图Fig. 13 Fusion index-time graph

由图13 可发现，600～1 200 s 噪声干扰段的变化与前600 s 无人干扰段的变化差异不明显，这是因为噪声信号距离采集器较远，与变压器正常信号相比较微弱，故对判断系统产生影响较小；后600 s 有故障信号出现时，融合指标发生剧烈变化，可检测出故障产生.

为了量化故障判断结果，绘制图14，得到的正常状态（包括噪声干扰信号）情况记为1；故障状态情况记为−1；前1 200 s 为正常状态，后600 s 为故障状态，由图14 可知，只有少数点判断错误，统计判断错误点，计算准确度为99.39%. 结果表明，该系统具有很好的故障判断能力.

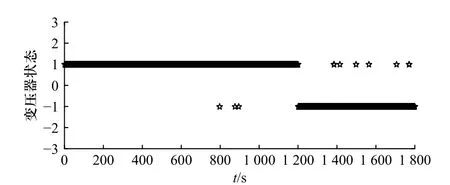
图14 变压器状态-时间散点图Fig. 14 Transformer status-time scatter plot

4 结 论

针对变压器可听声故障种类繁多、故障样本不足的问题，提出了一种基于声学特征融合的变压器故障判断方法，对变压器声信号进行一维特征融合并利用该特征进行故障识别，为变压器的故障早期发现提供一种思路，主要结论如下：

①采集大量的变压器正常声信号，利用mRMR算法从不同空间域中筛选出了有效特征，对这些特征进行加权熵主成分融合得到变压器融合指标，结果显示，融合指标区分明显，可作为声信号故障判断的唯一标准.

②对现场采集到的不同负载下的声信号进行融合指标转换，结果初步表明融合指标对负载变化不敏感，但220 kV 与110 kV 下的变压器融合指标区别较大.

③利用comsol 仿真软件仿真出220 kV 电力变压器下的绕组故障声信号，并转换为融合指标.结果表明：该故障融合指标与220 kV 正常融合指标区分明显，初步验证了利用融合指标进行故障判断的有效性，并与谱相关系数法、声波分析法对比，故障类别检测明显，验证了方法的优越性.在变压器故障判断系统测试，能够正确的判断故障，证明方法的可靠性.

基于本文的研究结果，下一步加入变压器的更多影响因素获取融合指标，进行深入研究.