液体火箭发动机的分层贝叶斯变分推理故障诊断方法

刘久富，丁晓彬，汪恒宇，王彪，刘海阳，杨忠，王志胜

（1. 南京航空航天大学 自动化学院, 江苏，南京 211106；2. 东南大学 电子信息工程学院, 江苏，南京 211189）

贝叶斯网络(Bayesian networks)[1−2]将概率论与图论相结合，通常以一种有向无环图的形式表现出来. 目前，贝叶斯网络已成为不确定性分析的工具，已被广泛用于处理各种问题，包括基因分析[3]、机器人控制[4]、故障诊断[5]、目标跟踪[6]、信号处理[7]和生态系统建模[8]等. 根据数据构建贝叶斯网络，需要大小适当的样本，具体取决于网络的拓扑和复杂性. 在某些情况下，如罕见疾病的诊断[9]、地震预测[10]和风险评估[11]等，收集大量数据很困难，此时通常将该领域的专家知识作为先验信息.

贝叶斯网络学习通常包含两个主要步骤：结构学习和参数学习. 结构学习通过建立有向无环图定义一个贝叶斯网络的结构. 参数学习则是对该有向无环图的每个节点的条件概率分布表进行估计.

为了提高参数学习算法的精度，近年来国内外学者对此作出了颇多贡献，主要有：DE CAMPOS 等[12−13]提出了一种适用于任何凸参数约束的约束最大熵方法. 通过创建了一种不精确Dirichlet 模型，将先验信息和数据集结合在一起，作为补充参数约束. CHANG等[14]提出用定性最大值后验方法来解决任何凸参数约束问题，将先验Dirichlet 分布的超参数确定为等效样本容量和采样参数平均值的乘积，采取拒绝接受采样策略从参数约束中抽取一定数量的参数.ZHOU 等[15]提出一种带约束的多项式参数学习方法.该方法对某些子节点和父节点的配置状态的频率进行统计，然后通过集成样本数据和参数约束来构建辅助贝叶斯网络模型. 肖蒙等[16]提出一种适用于多态节点和样本信息不充分情况下的改进贝叶斯网络参数学习方法，通过因果机制独立假设，对条件概率分布进行因式分解，同时将多态模型对算法的影响进行量化，最后从数据集中获取贝叶斯网络参数. 杨宇等[17]提出一种凸约束条件下的基于数据再利用的贝叶斯网络估计，充分利用数据的信息分类，将样本数据和先验知识灵活结合，深入挖掘两者之间的约束信息，从而提高参数学习的精度. 郭文强等[18]提出一种约束数据最大熵的贝叶斯网络参数学习算法，通过数据集估算贝叶斯网参数，将专家经验变为不等式约束，通过Bootstrap 算法得到参数候选集，最后利用最大熵进行加权计算.

上述方法中，由于多项式分布和狄利克雷分布的共轭性，参数估计非常有效. 但是，在一个节点上需要估计的条件分布的数量呈指数级大小，这些参数学习方法的精度在稀疏数据场景中受到很大影响，即使在具有中等规模变量的贝叶斯网络中，参数估计精度也不高.

本文基于传统的多项式-狄利克雷模型，通过引入超先验，构建分层多项式-狄利克雷模型，用于贝叶斯网络的参数估计，并引入变分推理算法用于优化模型. 以液体火箭发动机故障诊断为实例，将分层模型与传统模型对比，验证分层模型的有效性.

1 多项式-狄利克雷模型

1.1 传统的多项式-狄利克雷模型

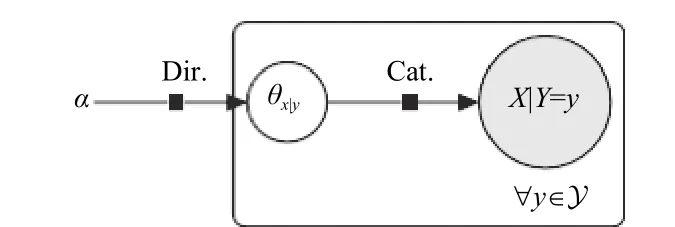
图1 传统的多项式-狄利克雷模型Fig. 1 The traditional polynomial-Dirichlet model

1.2 分层多项式-狄利克雷模型

图2 分层多项式-狄利克雷模型Fig. 2 Hierarchical polynomial-Dirichlet model

与采用简单的狄利克雷分布作为先验相比，这类先验可以改进分类分布的估计. 其中，式（4）中的先验值不能对y进行因式分解，因此不同的条件分布的参数不再是先验独立的.

1.3 参数的后验分布

2 优化求解

2.1 变分推理

θX|Y的后验分布不易处理，可以采用数值逼近的解决方案. 传统方法是通过马尔可夫链蒙特卡罗(Markov-chain Monte Carlo, MCMC)方法进行计算. 但是，在处理大型数据时，MCMC 方法需要大量的计算时间. 本文采用变分推理算法[20]（variational inference,VI），能够高效地估计参数的联合后验分布.

2.2 牛顿法求解τ

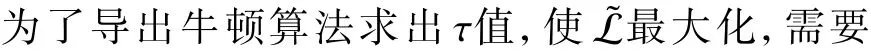
2.3 牛顿法求解τ

3 实例分析与验证

3.1 数据收集与属性选择

液体火箭发动机的工作过程主要分为启动过程、关机过程和稳态过程. 启动和关机过程主要是非线性时变的随机过程，需采用其他故障诊断与分类方法. 本文主要对氢氧液体火箭发动机的稳态工作过程的故障进行分类.

本文从试车数据中选择7 类易发生的故障类型，共包含22 个属性变量. 故障类型和属性变量如表1和表2 所示. 使用最小描述长度离散化方法对连续型数值进行离散化，将非数值型数据转换为数值型，且数据样本不含缺失值.

表1 液体火箭发动机易发生故障类型Tab. 1 Types of liquid rocket engines prone to failure

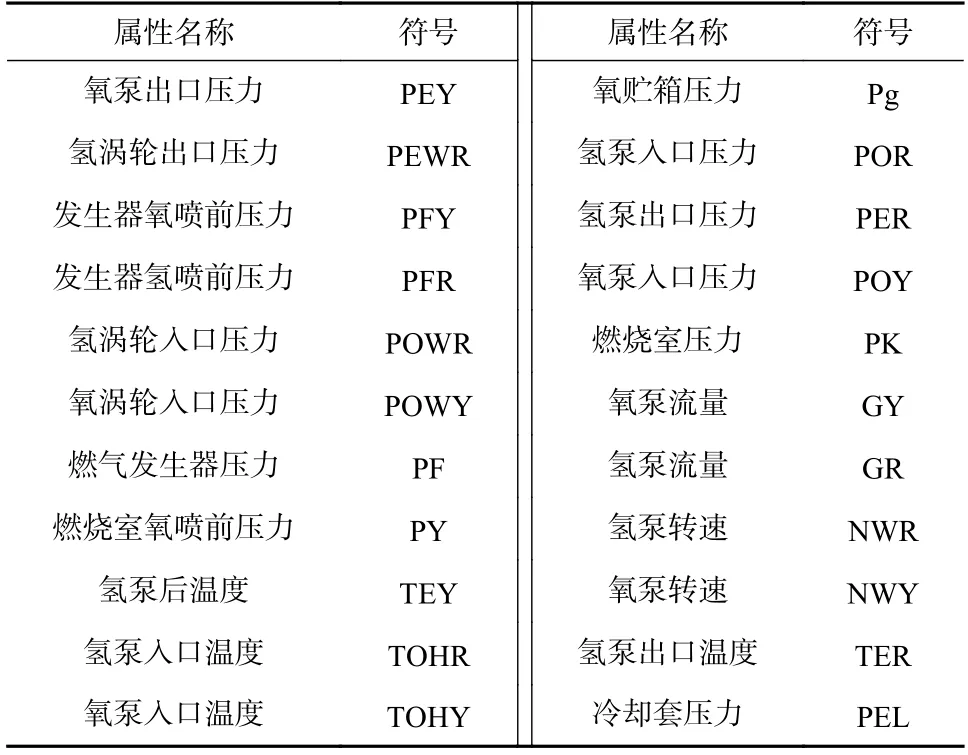
表2 特征属性选择Tab. 2 Feature attribute selection

3.2 故障分类模型建立

本文构建TAN 结构，首先按照式（14）计算条件互信息(conditional mutual information, CMI)

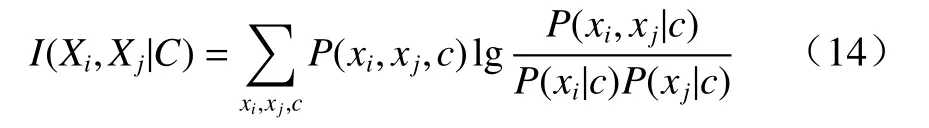
将表2 中的属性作为树的节点，将属性间的条件互信息作为节点间的边的权重，构建出最大生成树. 设置每条边的方向，并将类节点插入图中，使其指向每个属性节点. 由此构成的TAN 结构如图3 所示.

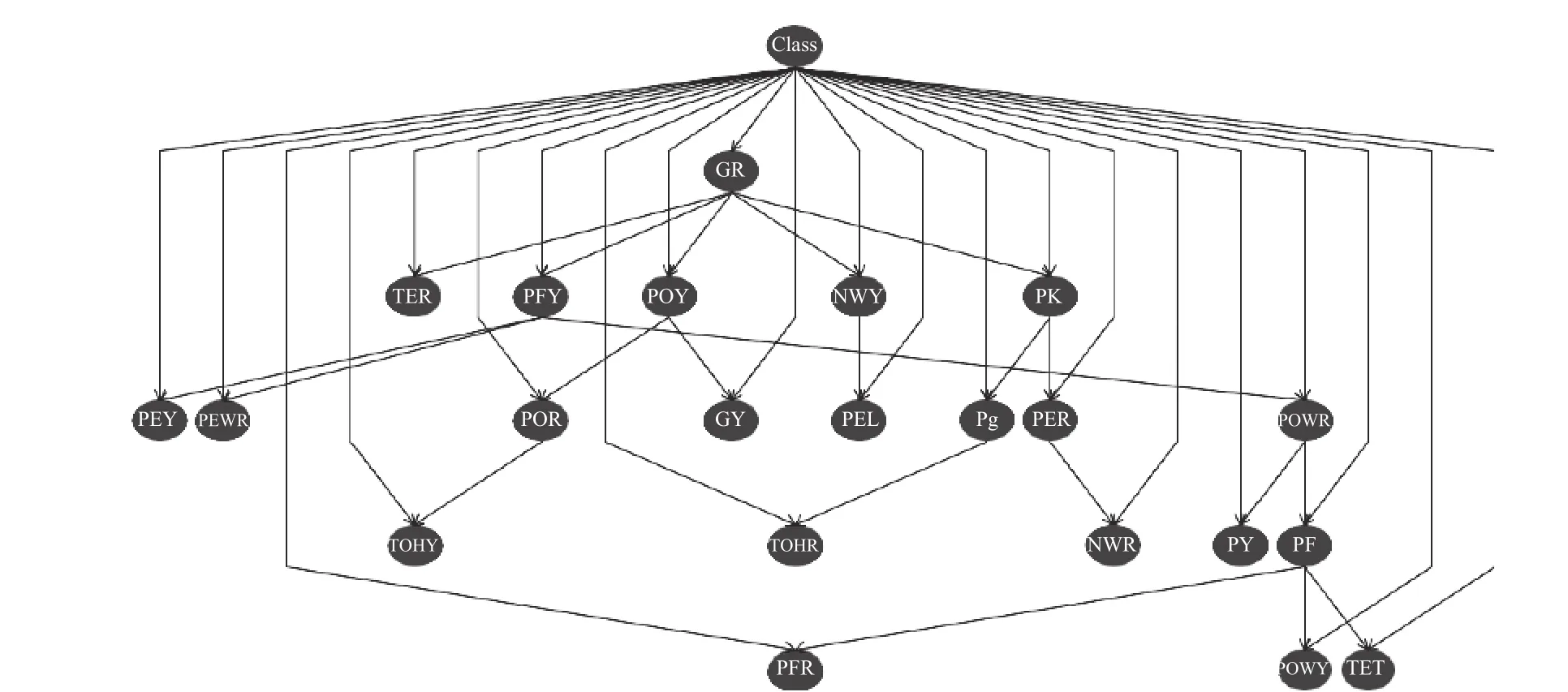
图3 液体火箭发动机故障分类的TAN 结构Fig. 3 TAN structure of liquid rocket engine fault classification

从图3 中可以看出，除了类节点外，每个节点至多只有一个属性节点作为其父节点. 各节点之间的依赖关系也大致反应出在实际情况下，属性之间的相互关系.

3.3 故障分类结果

为了验证不同样本量对传统模型和分层模型的影响，从液体火箭发动机故障样本中随机抽取n行数据构成训练集进行实验，其中n∈{20,40,80,160,320}.对于每个不同的n值，重复10 次以下过程：

①从液体火箭发动机故障样本中抽取n个实例构成训练集.

②从训练集中估计TAN 网络的参数.

③从液体火箭发动机故障样本中随机抽取不包含训练集的1 000 个实例，构成测试集.对测试集进行分类.

④对于传统的BDeU 先验，设置αx=(|У||X|)−∞进行参数估计. 对于分层模型，设置s=|X|和α0=11×|X|. 设置变分推理算法迭代的终止条件为迭代次数大于1 000 次或相邻两次迭代的差值小于10-6. 另外，除了均方误差，将KL 散度也作为衡量参数估计精度的指标，同时使用ROC 曲线下的面积衡量分类器的分类性能. KL 散度的计算公式为

表3 液体火箭发动机的故障数据的关联矩阵Tab. 3 Correlation matrix of failure data of liquid rocket engine

表4 故障分类评价指标Tab. 4 Fault classification evaluation index

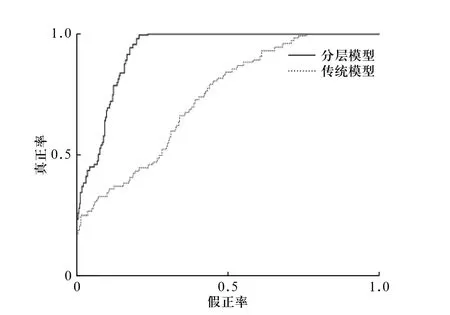
图4 分层模型与传统模型的ROC 曲线比较Fig. 4 Comparison of ROC curve between hierarchical model and traditional model

尽管训练样本集的实例数仅有20 个，但是建立的分层模型对实例数为1 000 的测试集进行分类，ROC 曲线下面积仍然达到0.939，而传统模型仅有0.732. 对比发现，当样本实例较少，相比于传统模型，分层模型对于贝叶斯网络参数估计的提升是巨大的.这也表明，分层模型用于贝叶斯网络的参数估计十分有效.

为了进一步比较两种模型各方面性能的差异，针对不同的样本实例数量，绘制了MSE、KL 散度和ROC 曲线面积图，如图5～图7 所示.

在图5 和图6 中，从MSE 和KL 散度的计算结果来看，分层模型在参数估计精度上优于传统模型，且当样本中包含实例数量越少，这种优势越明显. 尽管随着样本实例n不断增大，两者之前的参数估计精度的差异越来越小，但是分层模型的表现仍然优于传统模型. 从图7 中ROC 曲线的面积来看，分层模型具有较高的分类精度，且样本实例数量越少，差距越明显. 随着训练集样本实例数不断增加，分层模型的ROC 曲线下的面积接近于1，且分类结果较为稳定.

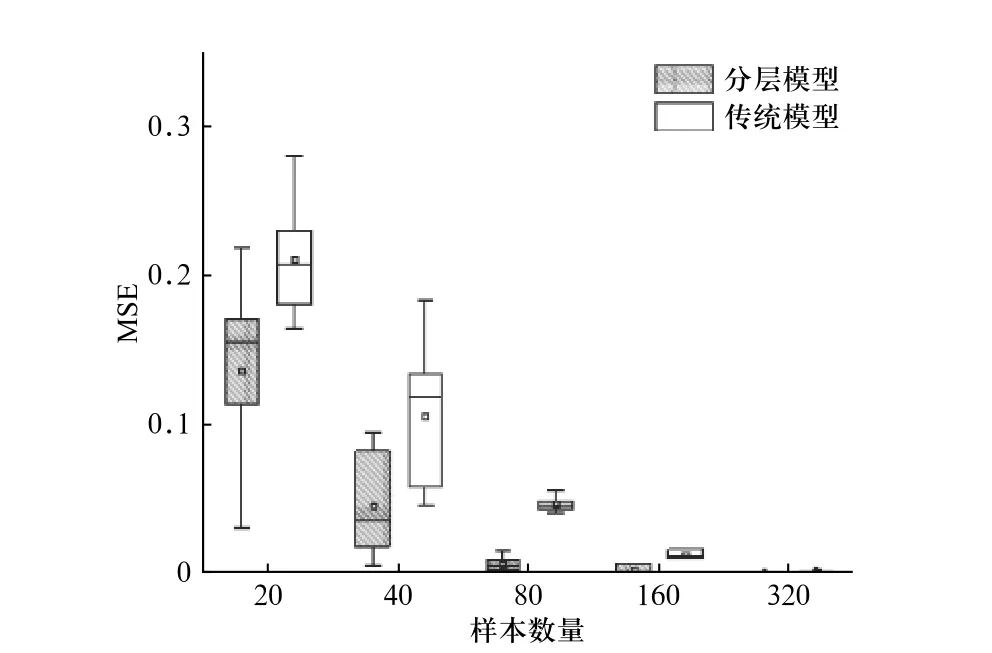
图5 分层模型与传统模型的MSE 箱型图比较Fig. 5 Comparison of MSE box plots between hierarchical model and traditional model

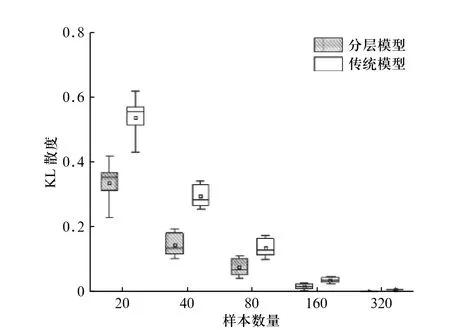
图6 分层模型与传统模型的KL 散度箱型图比较Fig. 6 Comparison of KL divergence box plot between hierarchical model and traditional model

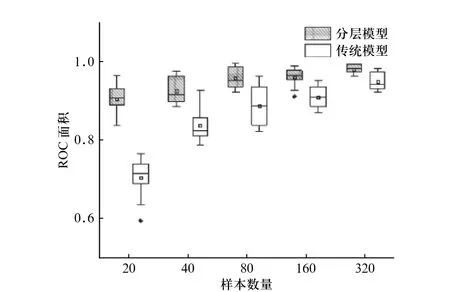
图7 分层模型与传统模型的ROC 面积箱型图比较Fig. 7 Comparison of ROC area box plot between hierarchical model and traditional model

4 结 论

①本文在多项式-狄利克雷模型中引入超先验，构建出分层模型用于贝叶斯网络分类器的参数估计.与传统的模型相比，本文提出的分层模型能够显著提高参数估计的精度，且训练样本越少，分层模型的优势越明显.

②本文将变分推理算法用于优化分层多项式-狄利克雷模型. 样本数量越少，变分推理算法在参数估计上的优势越明显. 当样本的特征属性的维数越多，变分推理算法在训练时间上的优势越明显.

③分层模型也可用于贝叶斯网络的结构学习中. 未来的研究工作是将结构学习中的分层模型与本文提出的参数学习中的分层模型结合起来，进一步提高贝叶斯网络分类器的性能.