卡尔曼滤波在农电网系统中的研究分析

王立达 韩成浩 陈冠文

(吉林建筑大学，吉林 长春 130119)

引言

近年来我国对农村电网全面建设发展，一些农村电网的安全性问题也暴露出来。严重影响农村电网运行的可靠性，给农村电网带来非常大的隐患[1]。在这些问题下对电网的预测与维护刻不容缓。农网最大的问题是电力系统频率的随机性与不确定性日益严重，导致谐波的频率也越发严重，如果不够重视将会导致重大事故[2]。通常应用傅氏检测方法(离散型傅里叶[3]变换或快速傅里叶变换(FFT))以及其改进方法。对频率控制是一种典型的滤波技术，目前应用最为广泛。但是在有含噪声的滤波方法以及跟踪技术中不适用。本文介绍应用卡尔曼滤波对给出的电力正弦[4]方程进行仿真，通过加装卡尔曼滤波器来分析图形，能更好地预测图形趋势。

1 卡尔曼滤波

经典最优滤波分为2类:Wiener滤波(采用频域方法)，卡尔曼滤波(时域状态空间方法)。维纳滤波与卡尔曼滤波的使用方法大不相同。Wiener(采用频域方法)这种滤波方法的条件相对要求比较高。其缺点和局限性是要求信号是平稳和随机的，所有应用数据都必须存储，并且滤波器也不是递归的。Wiener滤波计算量和存储量也比较大，很难在工程上适用单通道的随机信号。卡尔曼滤波是一种利用状态空间描述系统的时域滤波方法，算法采用推进法，数据存储量很小。不仅可以处理平稳随机过程，还可以处理多维非平稳信号。

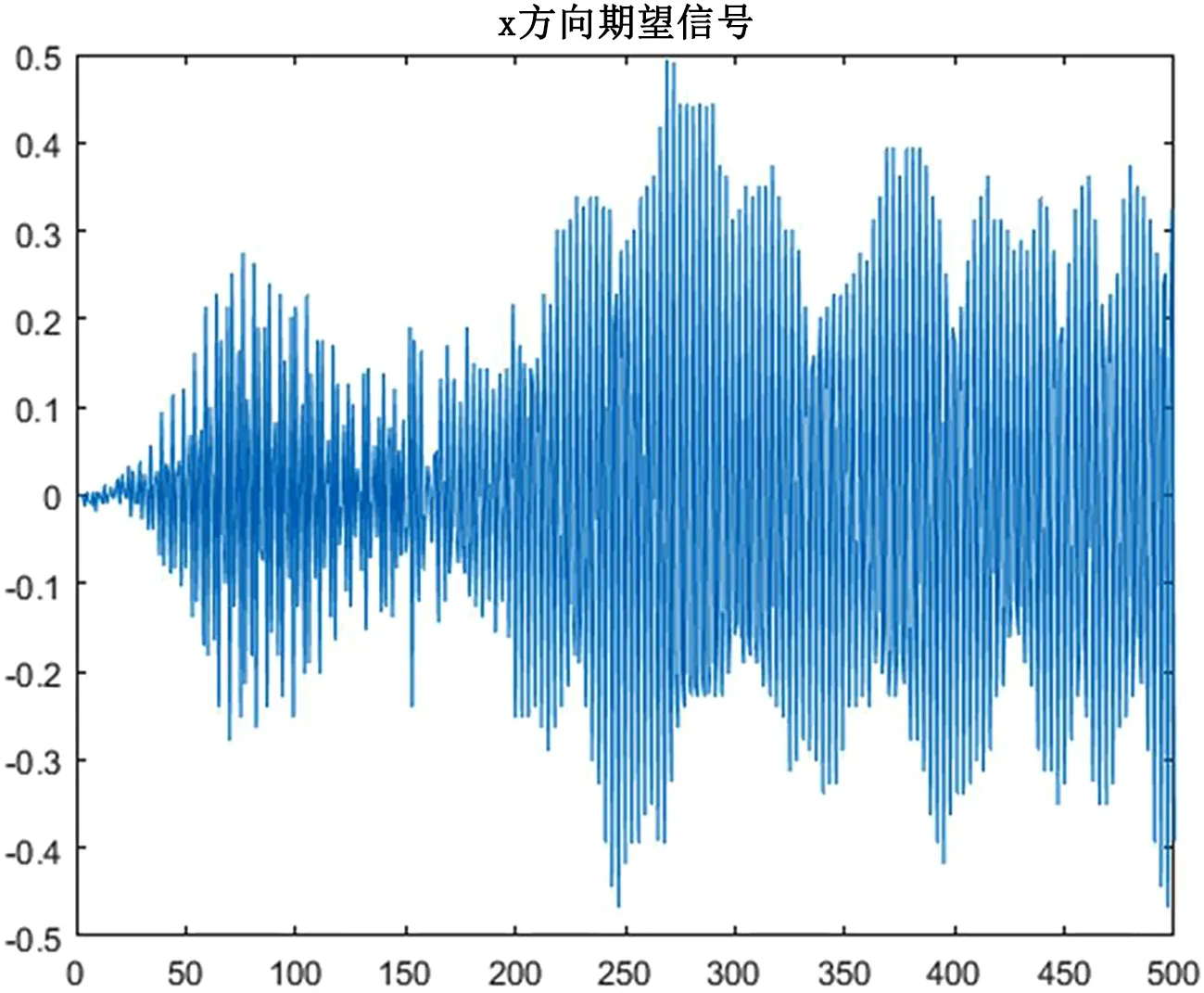
图1 原始波形序列

表1说明在原始波形序列中加入为维纳滤波后，信号的频率变得不稳定、波动很大。

表1 原始信号图形观测表

表2说明在原始波形序列中加入卡尔曼滤波后，信号的频率变得相对稳定、波动小。

表2 原始与卡尔曼滤波对比

在图2、图4中维纳滤波的信号没有卡尔曼滤波波形平稳，波动很大，显然加入噪声后卡尔曼滤波器对噪声跟踪频率的效果会好一些。上述实验是在频域与时域进行的，相对波形也较短。在电力系统中系统会产生噪声，而且电力系统的信号也不一定是单通道平稳的，所以采用卡尔曼滤波来进行。

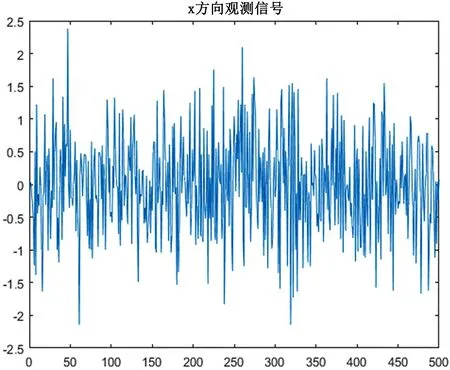
图2 原始波形加入维纳滤波

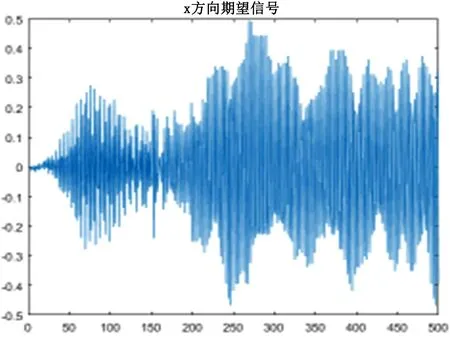
图3 原始波形

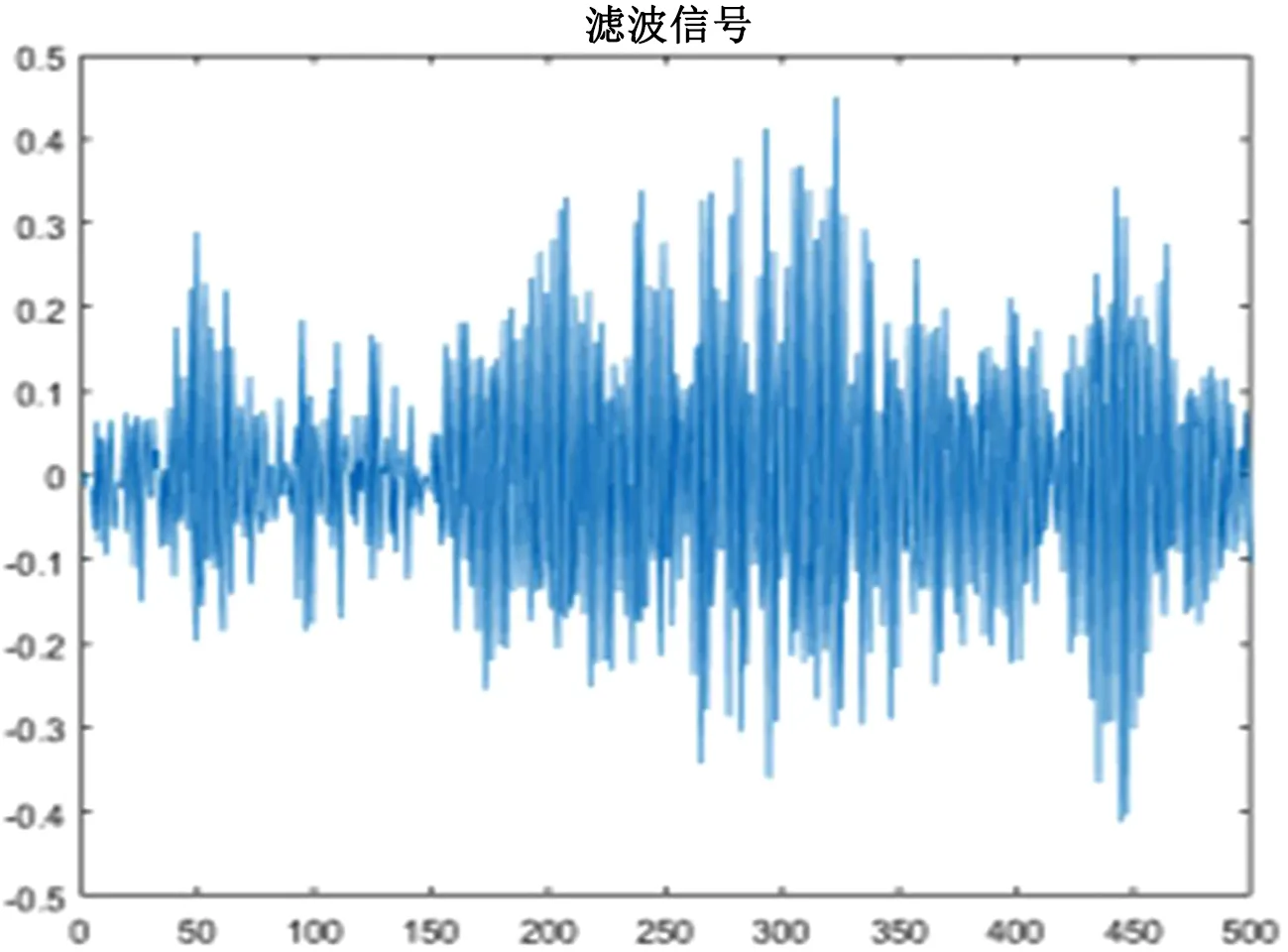
图4 原始波形加入卡尔曼滤波

经典卡尔曼滤波主要应用在线性系统中，扩展卡尔曼、无迹卡尔曼和交互多模型等滤波主要是应用在非线性系统中。计算机的不断创新使卡尔曼滤波器的计算要求和复杂性已不再是应用的障碍。非平稳信号和多维系统的滤波使用卡尔曼滤波器。由于卡尔曼滤波器还考虑了协方差P和卡尔曼增益K，因此研究动态谐波更为实用。

工程试验中应用卡尔曼滤波的前提是系统必须是可以观测的，也能够处理带噪声(高斯白噪声)的系统，但是系统要实时性的，这一点卡尔曼滤波就没有粒子滤波好(可以处理非线性系统)，不过粒子滤波过程比较复杂，但粒子滤波不用一直迭代公式，在分析工频抑制[5]时，通常会考虑结合其它软件程序。

如图5所示，在建立卡尔曼滤波处理过程的同时，也要获取数据，通过流程图可知，包括输入量、过程噪声2个输入量，输入量产生系统噪声，过程噪声设立状态参数并结合系统噪声最终传输到测量参数。这个过程会产生延时反馈给状态参数，最后得到预估值。

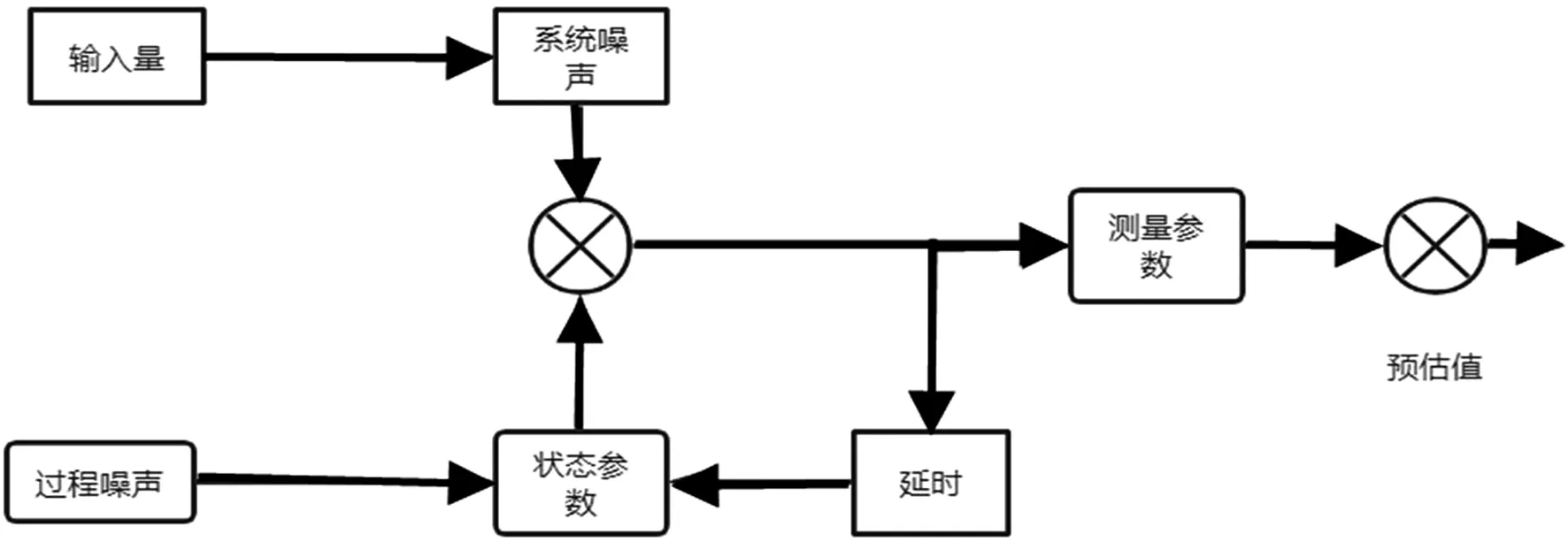
图5 卡尔曼滤波实验流程图

2 建立电力系统的卡尔曼滤波方程

2.1 线性卡尔曼滤波方程

线性卡尔曼滤波方程表示如下：

X(k+1)=AX(k)+W(k)

(1)

观测量Z(k)：

Z(k)=H(k)X(k)+V(k)

(2)

在上述公式中，可知系统的离散时间为k；系统n维状态向量为X(k)；对应状态的观测信号为Z(k)；系统输入的白噪声为W(k)；观测噪音为V(k)；状态转移矩阵A，观测矩阵为H(k)。

进一步预测:

X(k+1|k+1)=A(k|k)

(3)

状态更新:

X(k+1|k+1)=AX(k+1|k)+K(k+1)ε(k+1)

(4)

滤波增益矩阵:

K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1

(5)

一步预测协方差矩阵：

P(k+1|k)=φP(k+1|k)φTΓQΓT

(6)

必须考虑估计时的误差方差，否则加装滤波器看不出前后图形的比对。

估计的误差方差矩阵：

P(k)=(I-K(k)H(k))P(k)

(7)

2.2 基于谐波电力系统的卡尔曼滤波方程

第k次谐波的三相电压系统应考虑如下，其离散傅里叶级数的表达式：

(8)

式中，谐波分量的次数用k表示；第k次谐波分量的角频率为kω；k次谐波的有效值为Uak、Ubk、Uck；各相k次谐波分量相角分别用φak、φbk、φck表示;采样时间间隔为Δt，即采样频率为fs=1/Δt。

由式(8)可以写出三相系统电压的正序瞬时值对称分量为：

(9)

同理可得出其它2式。

正序谐波对称分量可表示为：

(10)

负序谐波对称分量可表示为：

(11)

上述式中，Up1为正序基本对称分量;Un1为负序基本对称分量。

对公式进行变换：

(12)

可得：

(13)

由多次谐波对称分量构成正序瞬时值对称分量，在测量信号中存在着干扰，通常对采样进行滤波处理以便减少估计误差，为滤波后谐波分量的最大频率[6]。

对式(9)进行变换：

jUp(m)ejnkωΔt=Up1ε(m)

(14)

(15)

式中，Up1为要估计的基本正序对称分量。

当ω未知时,可以把ω当成一个待估计的状态变量,这时需要对式(11)进行变换：

X(k+1)=X(k)+Z(k)

(16)

Z(k)=f(k,X(k))+W(k)

(17)

f(k,X(k))=UP1ejnkωΔt

(18)

Z(K)=Re|jUP(k)|+jIm|jUP(k)|=Z1(K)+jZ2(k)

(19)

(20)

(21)

式中，W(k)的均值为0，V(K)的均值也为0，方差为任意值的量侧系统和系统干扰，量侧系统和系统干扰为互不相干的高斯白噪声序列，其特点:E[W(k)]=E[Vk]=0；COV[W(k),Vk]=E[W(k)VkT]=0；E[W(k)WT(j)]=Rkδkj；E[V(k)VT(j)]=Qkδkj，Qk为非负定矩阵，Rk为正定矩阵。

3 电力系统的卡尔曼滤波仿真

为了验证卡尔曼滤波对频率噪声跟踪的正确性,对以下信号进行仿真。

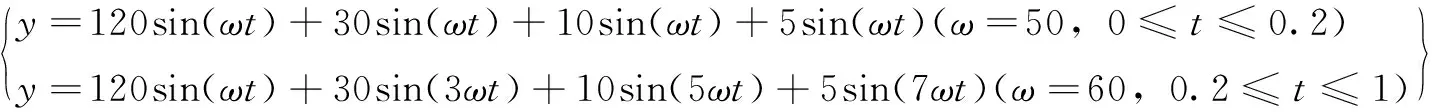
由上述给出的方程应用仿真程序如图6所示，图中的频率在0.2s之前为50Hz，0.2s之后变为60Hz。

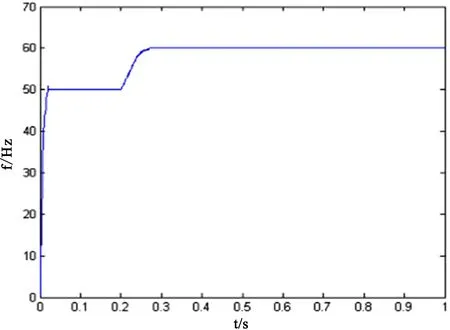
图6 电力系统仿真信号波形图

如图7所示，在将卡尔曼滤波应用到仿真中，在0.2s之前50Hz跟踪的波形也相应变化大，而在0.2s之后变为60Hz后滤波也随之变得平稳。跟踪误差也很小。其解决了电网信号异常时无法实现的问题，为电力系统的运行、控制系统及计算机仿真和调节奠定了基础。

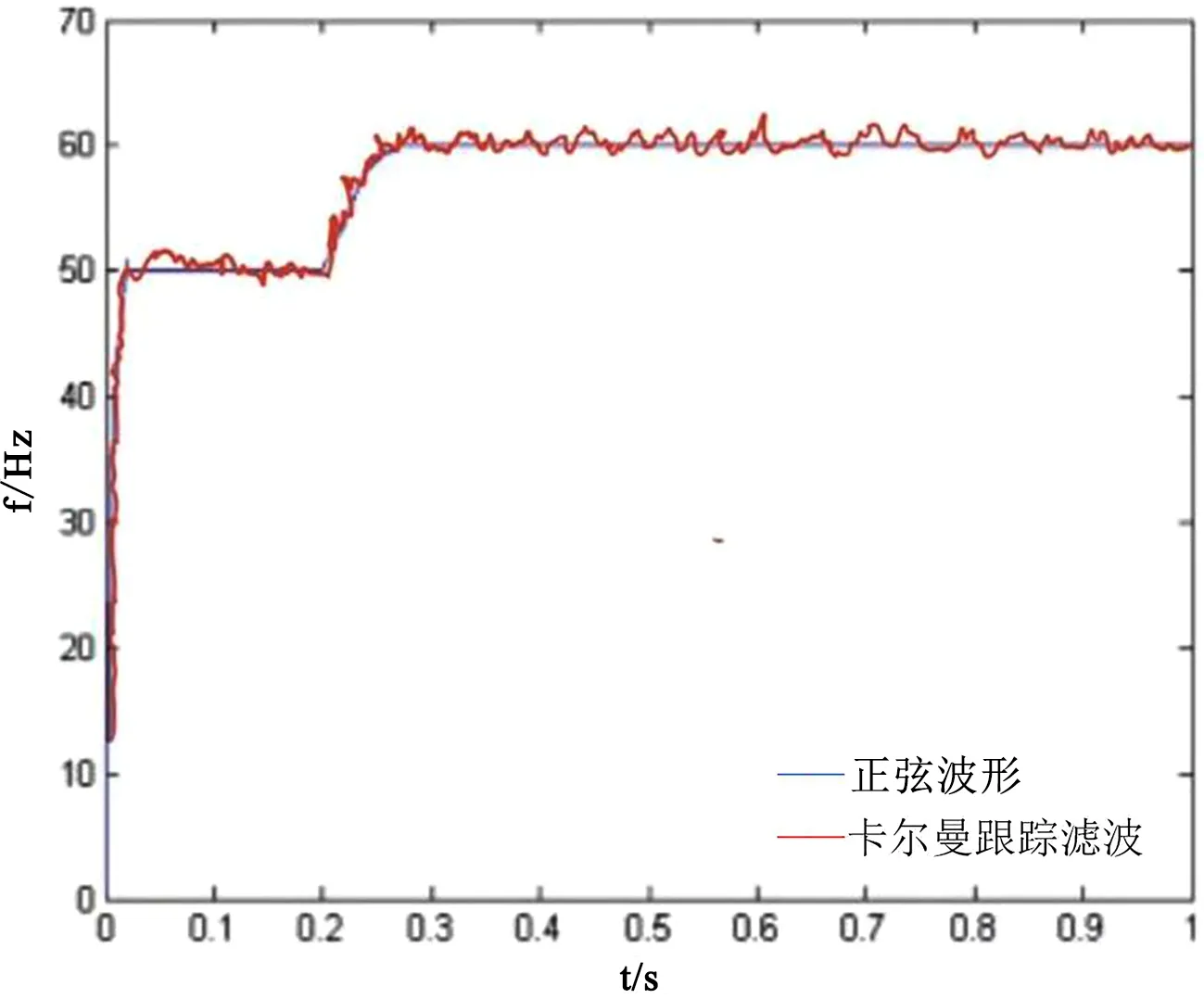
图7 加入卡尔曼滤波对噪声的追踪

4 结论

农村电网是电力事业发展的重要组成部分，也是“十四五”规划的重点，随着我国经济发展的日益提高农电网的规划与日俱增，做好农电网的管理，对于我国农业和农村发展、提高农村生活水平有着非常大的意义。本文对农电网系统分析是卡尔曼滤波以贝叶斯滤波原理为基础，利用方程组充分预测线性动态过程。应用卡尔曼滤波的原因是其具有强大的动态追踪能力、估计精度优良和抗干扰性好等特点，非常适用于谐波分量噪音小的动态估计。在应用卡尔曼滤波的基础上，应用对称三相电压的分析和转换,采用瞬时值对称分量分析法得到正序向量,用卡尔曼滤波实现基本估计。Matlab仿真结果表明,此方法利用卡尔曼滤波递推过程中系统噪声和观测噪声的大小,实现自适应方程的变化,缩小了初值的影响。确保系统安全运行，为农村现代化发展提供安全、可靠、稳定的电力。