解构中点问题提升数学理解

范建兵

[摘  要] 作为中考的高频考点，中点问题具有基础性、灵活性、模型化的表征. 教学时应关注学生读图、识图、解图、构图的能力，解读问题的本质，解构基本图形，挖掘问题模型，提炼解题策略，以提升学生的数学理解能力，提高学生的学习能力.

[关键词] 中点;中位线;问题意识;数学理解能力

线段中点是几何图形中的一个特殊点，在研究中考数学试题时发现，关于中点问题的考查比较突出，虽题多面广但指向明确，其一般有三类考查视角：①考查中点的定义，利用定义来表示两条线段相等或倍半关系;考查三角形中线的性质，利用等腰三角形或直角三角形的中线性质来解决实际问题;②考查三角形的中位线，利于三角形中位线的性质来呈现线段的位置或数量关系;③考查中點问题与其他知识点的融合，如垂直平分线、垂径定理等. 中点问题是初中数学教学的一个重点内容，常常会有不同层次的考题出现，其中大部分题目都被教师贴上了“基础题”的标签，学生练得多但想得少. 教学时，一些教师基本上就题论题，偶尔有少许研究但相对零乱、不成体系. 这就导致此类问题成了学生的学习弊端，对知识背景、来龙去脉关注不够，重结果而轻过程，缺乏问题意识，不利于创新精神和实践能力的培养.

案例分析

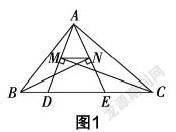
案例  （2018年四川省达州市中考数学第8题）如图1所示，△ABC的周长为19，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长为______.

1. 问题解构

一道几何综合题，往往考查的是较多知识的融合，以及较难的图形识别和较高的能力要求. 这道中考题的内容丰富，如果没有教师的帮助，大部分学生很难理解题意并突破难点. 在此，我们可以将图形进行分解，从寻找基本图形、剖析知识要点等方面对问题进行深度解构，帮助学生寻找解题方向，引导学生合理建构知识体系，以促进知识结构的完善和能力的提升.

（1）图形分解.

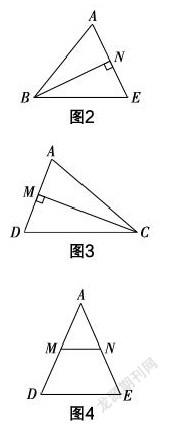
图形语言是一种重要的数学语言，蕴含着丰富的信息. 结合文字语言、符号语言实现三者之间灵活转换是解决几何综合题的关键. 从一个复杂的图形中剖析出一些简单的、基本的图形，有利于发现其中蕴含的知识点. 因此，可以从本题的原图（图1）中分解出图2、图3、图4三个简单的图形.

（2）图形解析.

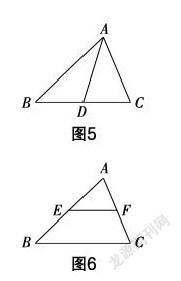
章建跃老师在“三个理解”中指出：理解数学是提高数学教学质量的前提，理解数学其中一个方面就是从表面到本质——把握问题的深层结构. 追根溯源，图2、图3、图4在平时的教学中是否出现过？分别应用了什么知识点？结合上面的图形与文字，我们容易关联思考到下面两个基本图形（图5和图6）.

图5是单中点基本图形，点D为BC的中点，线段AD为△ABC的中线;图6是双中点基本图形，点E，F分别为AB，AC的中点，线段EF为△ABC的中位线. 这两个知识点是初中几何的重要内容，融合性强，考查率高.

2. 问题解决

课程改革以来，我们一直在呼吁“要加强问题意识的培养，不仅要教会学生解决问题，更要教会学生提出问题、分析问题”. 对于教师而言，本案例的解决可能并不难实现;但对于学生而言，肯定是非常困难的挑战. 学生难在何处？本案例的本源在哪里？如何讲解本案例更有利于学生理解和掌握知识点？

细细读题并分析，我们可以发现本案例的内涵非常丰富. 表象上涉及了角平分线、垂线等显性知识，实质上却考查了全等三角形、等腰三角形及三角形中位线等知识. 通过图形解构，我们将图1转化为了几个基本图形，指向了两个重要的知识点. 因此，解决本案例需要我们引导学生将图形与知识关联思考：求线段长的常用方法有哪些？图中的角平分线和垂线该如何应用？所求线段MN与谁有关？与题中的已知线段BC和△ABC的周长有什么关系？通过“问题串”让学生寻找图1所隐含的基本图形，思考问题解决的常用策略.

通过对图2的思考，可以证明△ABN≌△EBN，从而得到点N是线段AE的中点;通过对图3的思考，可以证明△ACM≌△DCM，从而得到点M是线段AD的中点;通过对图4的思考，可以发现MN是△ADE的中位线. 因此，求线段MN的长就转化为求线段DE的长，而DE=BE+CD-BC=AB+AC-BC=AB+AC+BC-2BC=19-14=5，所以MN=2.5.

3. 知识重构

皮亚杰认为：认知不是直观的描摹，不是主体被动地接受，而是主体主动地用已有的认知结构去同化外部事物，在头脑中对外部事物进行加工、改组、转换、比较、分析、综合，以此来形成认识[1].

（1）图形比较.

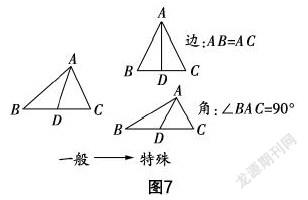
图5是单中点问题的一般图形，图2（或图3）是特殊三角形，这两个图形之间是否有联系？通过思考、改组、加工发现：对于一般状态下的△ABC（图5），如果△ABC的边AB=AC，那么△ABC就是等腰三角形，可以得到等腰三角形“三线合一”的性质;如果△ABC中的∠BAC=90°，那么△ABC就是直角三角形，可以得到直角三角形“斜边上的中线等于斜边的一半”的性质. 这样的融合与比较，蕴含了“从一般到特殊”的数学思想方法，也展现了几何图形之间的内在关联（如图7所示）.

图6是双中点问题的一般图形，EF是△ABC的中位线. 如果将三角形转换成四边形（如图8所示），可以得到中点四边形EFGH是平行四边形;如果将四边形改为矩形、菱形、正方形，那么中点四边形也会相应改变. 这个中点四边形的判定结果依据的就是基本图形（图6），运用了三角形中位线的性质，体现了问题解决的转化与综合. 此处需要说明的是，在解决四边形问题时，我们常常将四边形问题转化为三角形问题进行解决，此处对中点四边形的判定就是一个典型的应用案例.

（2）模型提炼.

学生的数学学习应该在已有认知结构上不断关联和引申，从中提炼问题模型，可以使学生丰富认知结构，完善知识体系[2]. 图2（或图3）就蕴含了一个重要的数学模型：“平分”加“垂直”构造了“等腰三角形”. 这个命题可以详细地表述为：如图9所示，BD平分∠ABC，点E是射线BD上一点，过点E作MN⊥BD，则△BMN是等腰三角形.

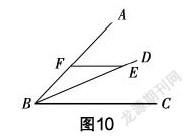
在数学课本上还有一个类似的模型：“平分”加“平行”构造了“等腰三角形”. 这个命题也可以详细地表述为：如图10所示，BD平分∠ABC，点E是射线BD上一点，过点E作EF∥BC，则△BEF是等腰三角形.

可以说，这两个模型在练习中考查的频率还是很高的. 平时教学中，教师应该有意识地指导学生从问题中提炼一些解题模型，归纳一些常用方法. 这既能丰富学生的知识结构，又能提升学生分析问题与解决问题的能力，有助于学生综合能力的提升与数学素养的发展.

（3）图形重构.

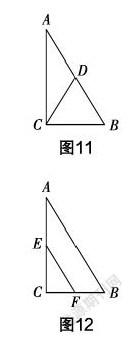
除了图形的识别与模型的提炼，我们还需要有图形重构的意识，让学生能多角度进行理解，以更好地掌握问题的本质. 比如，图11表示的是直角三角形斜边上的中线等于斜边的一半，图12表示的是三角形的中位线，如果将这两个图形组合、重构，形成一个新的图形，就是一个具有基础性、代表性的题目：如图13所示，△ABC中，∠ACB=90°，点D，E，F分别为三边的中点，证明CD=EF.

（4）经验再生.

为了让学生在问题探究和问题解决中加深对模型的认识，实现知识及时巩固、经验再生的教学功能，笔者选择了以下几个练习题（均为常见题），指向了不同中点问题以巩固和提升知识结构. 通过自我思考、练习、反思，学生可以从问题的解决、类型的识别、模型的应用等不同层次上抽象出属于自己的解题经验，这符合学生的认识规律，能促进学生全面、可持续发展.

练习题1：如图14所示，已知△ABC中，BD平分外角∠ABF，AD⊥BD于D，CE平分外角∠ACG，AE⊥CE于E，连接DE. 若AB=7，AC=6，BC=5，则DE的长为_____.

练习题2：如图15所示，已知△ABC中，D是BC边上的中点，AE平分∠BAC，CE⊥AE于E. 若AB=7，AC=4，则DE的长为______.

练习题3：如图16所示，在四边形ABCD中，AB=CD，AC，BD是对角线，E，F，G，H分别是AD，BD，BC，AC的中点，连接EF，FG，GH，HE，则四边形EFGH的形状是（      ）

A. 平行四边形       B. 矩形

C. 菱形                   D. 正方形

练习题4：如图17所示，已知△ABC中，BE，CF分别是边AC，AB上的中线，BE与CF相交于点O，则BO与OE的长度有什么关系？

教學思考

作为一个中考的高频考点，中点问题的知识点本身并不困难，难在知识综合和图形分解. 这就需要教师在讲解典型例题时讲明问题的本质，讲清基本图形，引导学生理解其中蕴含的数学思想方法，掌握一般的解题策略，再次遇到类似问题时才能引发关联思考并解决问题.

1. 高频考查的缘由

为什么中点问题能够成为高频考点呢？挖掘中点问题背后的特征，探寻命题中的能力与素养的立意，可以让教学的站位更高一些，目光更远一些.

（1）基础性：知识点相对单一，结论不多且通俗易懂，大部分学生都能够理解并掌握.

（2）灵活性：知识点的关联性、融合性强，可与初中学段的大部分知识点联合起来命题.

（3）模型化：中点问题的本源是两个基本概念和两个基本图形，分别对应的是中线和中位线，学生易于辨认，模型解决的策略也相对明确.

2. 渗透常用思想方法

上述案例的解决，涉及了多种数学思想方法，如转化思想、分类思想、建模思想等. 比较突出的是转化思想，在解题中将四边形问题转化为三角形问题，将未知问题转化为已知模型，将复杂问题转化为简单问题，等等. 数学思想渗透在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括. 在解题教学中，只讲逻辑而不讲思想，会使题目之间缺乏联系的纽带，导致学生的数学认知结构不完整或缺乏整体性.

3. 掌握一般解题策略

教学中我们习惯于给予学生方向性的指导，比如单中点问题常用倍长中线法，多中点问题常构造中位线，等等. 其实学生解题的最大困难并非不知道方向，而是没有读懂题意，不知道从哪里下手，或者缺少模型化意识，没有找到基本的、普遍适合的解题方法.

对于上述案例这样的几何问题，可以借助于图18的思考路径，指导学生从读题和识图两个方面入手. 读题不仅是读懂已知和未知，还要读出已知与未知的关联，需要仔细思考：题目的已知条件有什么用处？与学过的什么知识点有关？有没有做过类似的题目？引导学生用较短的时间去回忆和想象，寻找自己已有的解题体验. 同样，识图不仅仅是识别图形，还包括分解图形（寻找熟悉的基本图形）、图形重构（在原图形之外重新画出一个新的图形进行局部分析）. 这样的分析、寻找、思考的过程对典型题目的讲解很有必要，教师要舍得花时间，让学生去试一试、想一想，这是一个丰富的、有意义的过程. 此外，在解题教学中，应该全面关注学生的认知能力和理性精神，不能一味地讲技能、技巧. 只有教师教学时注重对基本图形的提炼，学生才会从复杂的图形中抽象出基本图形;只有教师教学时注重对基本方法、普适性方法的概括和总结，学生才能从更好的、更合理的解题视角去分析问题. 学生解题不是机械模仿，而是自主思考和独立思考，这样数学思维层次才能更高，学习效果才能更好.

参考文献：

[1]韩立福. 当代国际教育理论基础导读[M]. 北京：首都师范大学出版社，2006.

[2]张跃飞. 深度解构析错因，合理建构育素养[J]. 中学数学教学参考，2019（14）：34-36.

3283501908274