矩形天线阵OAM波产生与优化

杨冬华，王 洋，刘 杰，揭文军，廖 希，金 纯

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 移动通信教育部工程研究中心，重庆 400065；3.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

0 引 言

根据电磁轨道角动量(orbital angular momentum, OAM)物理属性可知，携带不同拓扑荷的OAM波彼此正交。应用于无线通信领域时，OAM可以实现多个数据流的同时传输，在提升频谱利用率和系统容量上存在巨大的潜力，受到研究者广泛关注[1-3]。

目前，在无线通信领域，OAM波的产生方式主要有螺旋相位板[4-5]、均匀圆形阵列[6](uniform circular array, UCA)和螺旋相位反射面[7]等。其中，UCA是利用移相器[8]来控制天线阵元间的相位延迟产生OAM波。然而，基于矩形阵列的多输入多输出技术 (multiple-input multiple-output，MIMO)不便于与基于UCA的OAM波复用结合。

此外，涡旋电磁波的发散性随着模值的增加而增大，降低了系统容量。为了解决发散性问题，文献[9]用UCA产生不同模态的OAM波束，并通过透镜达到汇聚波束的效果，增加了系统容量，代价是系统的构造成本上升了。文献[10]设计抛物面天线来汇聚由UCA生成的涡旋电磁波，并获得联合OAM和大规模MIMO通信的倍增频谱效率增益。该方案使用抛物面天线来实现涡旋电磁波汇聚，进而实现更好的频谱效率，但是收发电路设计的复杂度提高了。文献[11]设计了一种由圆形天线阵列、超表面构成的OAM波束汇聚系统，其中天线阵列作为OAM波束发生器，超表面被放置在距离阵列2λ处，以补偿涡旋波束的相位。实验结果表明，在频带为9.3～10.3 GHz时，该汇聚系统可以减小模式为1的涡旋波的发散角，波束发散性明显改善，同时增益从9 dBi提高到15 dBi，传输效率保持在75%以上，模态纯度降低约1%。但是由于超表面采用的是谐振材料，能够实现的带宽相对较窄。

对于OAM波束的汇聚，事实上还可以从天线阵列本身出发，在不改变原始波前相位的情况下，通过优化设计天线阵列同样可以达到波束汇聚的目的。稀疏优化技术在MIMO领域中已得到广泛应用，用于稀疏优化的算法包括蚁群优化(ant colony optimization, ACO)[12]、遗传算法(genetic algorithms, GA)[13-14]和粒子群优化(particle swarm optimization, PSO)[13]等。采用稀疏优化方法，不仅可以减少天线数量从而降低信号处理复杂度，而且能达到降低旁瓣电平(side lobe level，SLL)的效果。因此，开展对天线结构进行优化以达到将功率向主瓣方向收敛的研究是有必要的。

本文给出一种基于大型平面矩形阵列生成OAM波的方法，针对波束的发散性问题，将稀疏优化的思想用于优化阵列，使整个阵列的性能得到较大的提升，且系统结构不会因此而变得过于复杂。

1 系统模型

1.1 均匀圆形阵列

图1展示了均匀圆形阵列的几何结构。N个相同阵元均匀分布在圆周上;递增相位延迟按顺时针或逆时针方向添加到阵元。为了产生模态为l的OAM波束，要求所有阵元等幅馈电，相邻阵元激励存在δφ=2πl/N的相位差。根据电场的叠加原理，上述阵列产生的归一化电场可以表示为[6]

(1)

(1)式中:θ表示俯仰角；φ表示方位角；r是原点到观测点之间的距离;Rn表示第n个阵元到观测点间的距离;k=2π/λ为波数; 第n个阵元对应的相位为φn=2πnl/N。一般而言

Rn=(r2+a2-2arcosψ)1/2

(2)

当r≫a时，(2)式可以表示为

(3)

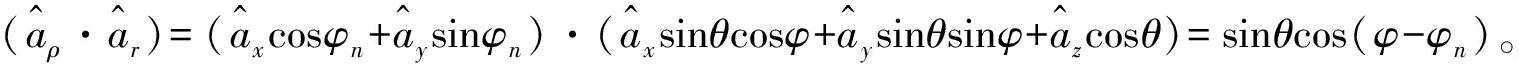
(4)

图1 均匀圆形阵列几何结构Fig.1 Geometry structure of uniform circular plane

1.2 矩形阵列

MIMO技术已在通信领域中广泛应用。然而，基于矩形阵列的MIMO系统不易与使用UCA生成的OAM相结合。在本节中，将采用相控阵技术实现矩形阵列生成OAM波。

根据图1的天线阵列，可以得到[15]

(5)

(5)式中:An为第n个阵元的幅值;(θ0,φ0)为波束指向角。

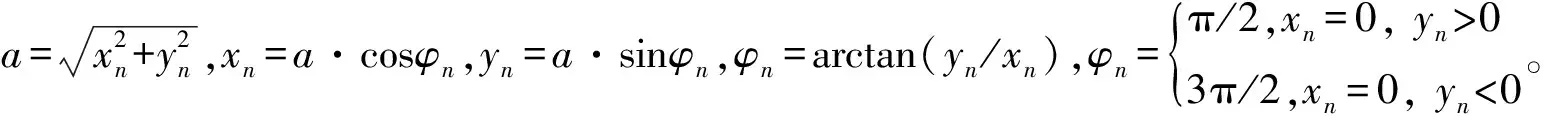
(6)

(6)式中:Iik表示第(xi,yk)个阵元的幅值;(x1,x2,…,xN)=((1-N)dt/2,(3-N)dt/2,…,(N-1)dt/2)为阵列元素在X轴上的位置;(y1,y2,…,yM)=((1-M)dt/2,(3-M)dt/2,…,(M-1)dt/2)为阵列元素在Y轴上的位置;dt是相邻两个阵元间的间距;φik=arctan(yk/xi)表示第(xi,yk)个阵元的方位角。

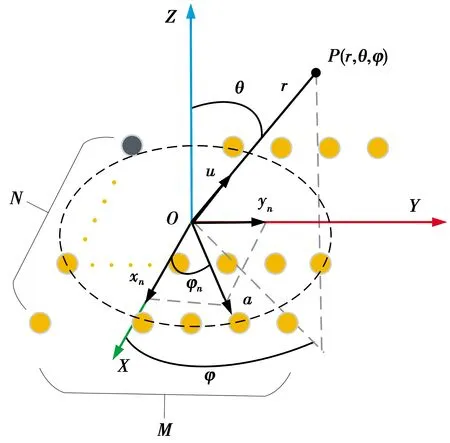
图2 矩形阵列几何结构Fig.2 Geometry structure of rectangular array

在仿真中，所有的阵列元素都是全向的，相邻两阵元间距是相等的。关键参数如下:f=3 GHz,dt=λ/4,M=N=8。

图3展示了不同OAM模态的相位图和强度图。由图3可知，利用方形阵列可以产生OAM波。与常规平面波相比，OAM波呈环形强度分布。

携带不同拓扑荷的涡旋电磁波是相互正交的，可以同时同频复用多个通信信道。天线阵可以实现灵活的OAM波束可调，但是一般需要额外射频相移模组，随着阵元数目的增加，整体成本与实现难度急剧增高。

2 稀疏平面阵列

OAM波的SLL会使天线辐射信号能量损失，这将严重降低OAM波在无线电通信和雷达等方面的应用性能。本文采用稀疏矩形阵列遗传算法(sparse rectangular array genetic algorithm, SRGA)抑制副瓣，特别是第一副瓣和第二副瓣。

2.1 优化模型

针对传统矩形阵列中存在的SLL问题，提出矩形阵列稀疏优化的方法。假设天线阵元在开和关之间进行切换

(7)

(7)式中，Tik表示第(xi,yk)个阵元的工作状态。本文假定稀疏平面阵列的孔径不变。稀疏率可以定义为

ζ=Q/M/N

(8)

(8)式中，Q是激活的天线数量。故有

(9)

S1表示θ=θ0时方位向方向图的旁瓣区间，如果方位向方向图的主瓣的零功率点为2φ0，则有

S1={φ|φmin≤φ≤φ0-φ0∪φ0+φ0≤

φ≤φmax}

(10)

S2表示φ=φ0时俯仰向方向图的旁瓣区间，如果俯仰向方向图的主瓣的零功率点为2ψ0，则有

S2={θ|θmin≤θ≤θ0-ψ0∪θ0+ψ0≤

θ≤θmax}

(11)

本文在优化过程中仅考虑对方位向的波束进行优化，根据最大旁瓣电平(maximum side lobe level，MSLL)的定义，将适应度函数定义为方位向最大旁瓣电平

(12)

目标函数CF可以表示为

(13)

图3 不同OAM模态的相位图和强度图Fig.3 Phase diagram and power map ofdifferent OAM modes

2.2 稀疏算法

基于GA的稀疏优化阵列算法如下。

输入：种群数NP，交叉概率Pc、变异概率Pm，迭代次数G，进化迭代数g，期望适应度值CFq

输出：最佳个体Tbest

1:随机产生种群T=[T1…Ti…TNP]H，将公式(13)设置为适应度函数fitness

2:while g<=Gdo

3: whilei<=NPdo

4: 计算CFi=fitness(Ti)

5: ifCFi<=CFq

6: 结束程序，输出Ti

7: end if

8: 轮盘赌法选择部分适应度较高的个体

9: 交叉

10: 变异

11:g=g+1

12:end while

实现SRGA的具体步骤如下。

1)输入种群规模NP、交叉概率Pc、变异概率Pm以及迭代次数G等参数；

2)随机产生T=[T1…Ti…TNP]H总种群集合，根据(13)式设计适应度函数，每个个体对应一个待求解问题的潜在解，进化迭代数g=1；

3)计算每个个体的适应度，判断最优适应度值是否达到目标，若达到，将最优适应度的个体作为最优解输出，算法结束，否则进行下一步；

4)根据个体的适应度，采用轮盘赌法选择部分适应度较高的个体进行后面的遗传操作；

5)对选中的成对个体，以概率Pc进行数值交换，产生新的个体；

6)对选中的个体，以概率Pm重新设置为新的潜在解，产生新的个体；

7)经过遗传操作后的群体作为新一代种群，g=g+1，并转到步骤(3)。

3 稀疏阵列的OAM-MIMO系统信道模型

3.1 OAM-MIMO系统模型

对于由Nt=M×N个发射天线和Nr个接收天线组成的视距(line of sight, LOS)无线通信系统而言，LOS OAM-MIMO通信系统模型见图4，其输入输出的关系可表示为[16]

y=HMtX+w

(14)

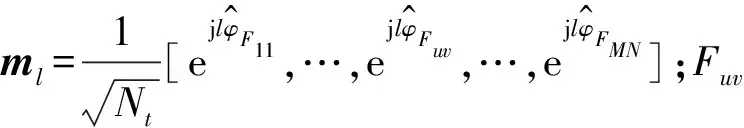
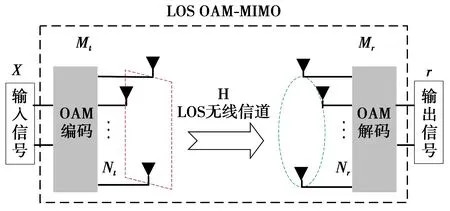
图4 LOS OAM-MIMO通信的信号模型Fig.4 Signal model for LOS OAM-MIMO communication

在接收端，采用发送方法的逆过程接收OAM信号，因此，接收端的输出矢量为

r=Wry=WrHMtx+ω

(15)

HOAM=MrHMt

(16)

3.2 稀疏阵列下的OAM-MIMO系统模型

本文将稀疏阵列技术应用到OAM-MIMO系统中，将有限的射频链路转换成天线子集上发射信号，按照一定的准则从Nt个发射天线中选择NF个最优天线，构成新的信道矩阵HOF。在新的信道矩阵中用0元素表示被删除的列，对应被删除的发送天线[17],故有

(17)

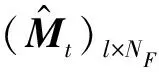
(18)

假定每个发射天线是等功率传输的，那么稀疏阵列下的OAM-MIMO系统的容量可以表示为

(19)

4 实验与分析

仿真参数设置如下：所有阵元都是等幅全向性的，发射端相邻两个天线间的间距dt=λ/2，阵列的工作频率f=3 GHz，发射天线M=N=8，最大遗传迭代次数G=100，种群数NP=50，交叉率Pc=0.7，变异率Pm=0.01，OAM模态数l=1，带宽1 MHz，系统总的发射功率是相同的且平均分配到每个发射天线上，接收阵列为UCA，接收天线数目Nr=34，接收阵列的半径Rr=λ。稀疏前后阵列的空间位置分布情况见图5。

4.1 对称稀疏优化下不同稀疏率的SLL对比

使用SRGA对所有阵元进行稀疏布阵，使稀疏后的CF值最小，可得表1数据。从表1可以看出，与原始阵列相比，稀疏后的阵列旁瓣降低1～2 dB。当稀疏率为0.75时，效果最佳。

表1 不同稀疏率的SLL对比Tab.1 Comparison of SLL of different sparsity rates

图5 稀疏前后阵列的空间位置分布Fig.5 Spatial arrangement of planar array and sparsely optimized array

4.2 对称稀疏优化下不同阵列SLL对比

图6为优化前后涡旋波波前归一化功率对比图。从图6可以看出，与原始阵列相比，采用激活阵元阵列产生的OAM波中心空洞大小基本不变。由于注销阵元阵列近似形成了一个UCA，故出现了类似于圆的强度分布图。

图6 优化前后涡旋波波前归一化功率对比图Fig.6 Power distribution contrast diagram of OAM wavefront before and after optimizing

平面阵列及对称稀疏优化后，阵列的辐射方向图如图7所示，阵列的SLL如表2所示。

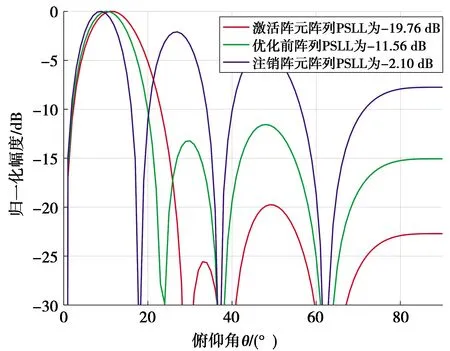
图7 平面阵列及对称稀疏优化后阵列的辐射方向图Fig.7 Radiation pattern of planar array and array optimized by symmeyric sparsity

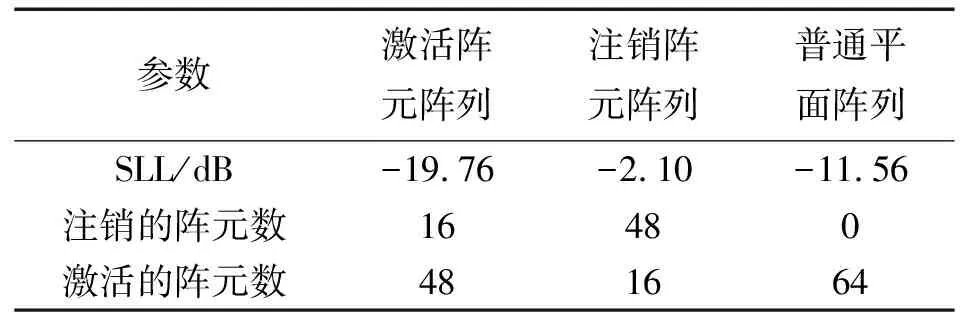
表2 不同阵列的SLL对比

从图7和表2可以看出，与原始阵列相比，激活阵元阵列的峰值旁瓣电平(peak side lode level, PSLL)降低70%。受到相邻两个阵元间间距较大的影响，注销阵元阵列的SLL数值较高。

4.3 非对称稀疏优化下不同阵列SLL对比

为了进一步分析阵列对称性和削减的阵元数对稀疏优化结果的影响，对阵元数Nt=100的方形阵列进行稀疏化处理。

图8为平面阵列及非对称稀疏优化后阵列的辐射方向图。从图8可知，在阵元总数减少45%的情况下，相比于原始阵列，激活阵元阵列PSLL减少了8.7%。与图7的对称稀疏优化相比，受到阵元分布位置的影响，非对称稀疏优化产生的OAM波波束电平分布不规则。

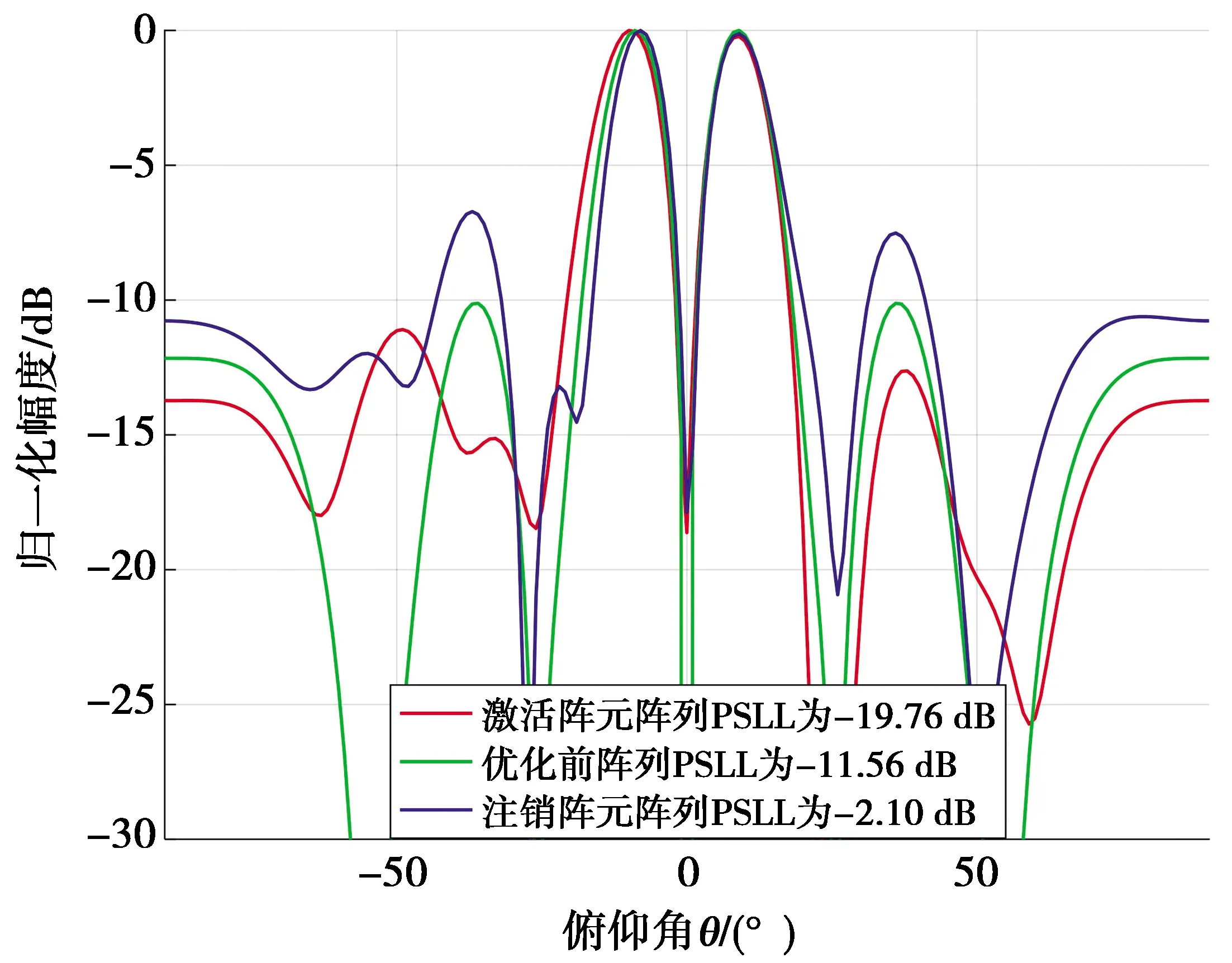
图8 平面阵列及非对称稀疏优化后阵列的辐射方向图Fig.8 Radiation pattern of planar array and array optimized by asymmeyric sparsity

4.4 对称稀疏优化容量对比

图9是稀疏优化前后，OAM信道l=1的系统容量随着传输距离的变化曲线图。其中发送端为矩形阵列，稀疏天线数量NF=48，信噪比SNR=25 dB。由图9可知，OAM波的系统容量随着传输距离的增加而减少。采用图5b的稀疏阵列作为发射阵列，当传输距离10≤D/λ≤12时，激活阵元阵列的信道容量与稀疏前非常逼近。当传输距离D/λ>15，接收阵列落在如图6c所示的波束主瓣与旁瓣间的凹处，致使注销阵元阵列的信道容量几乎等于0。

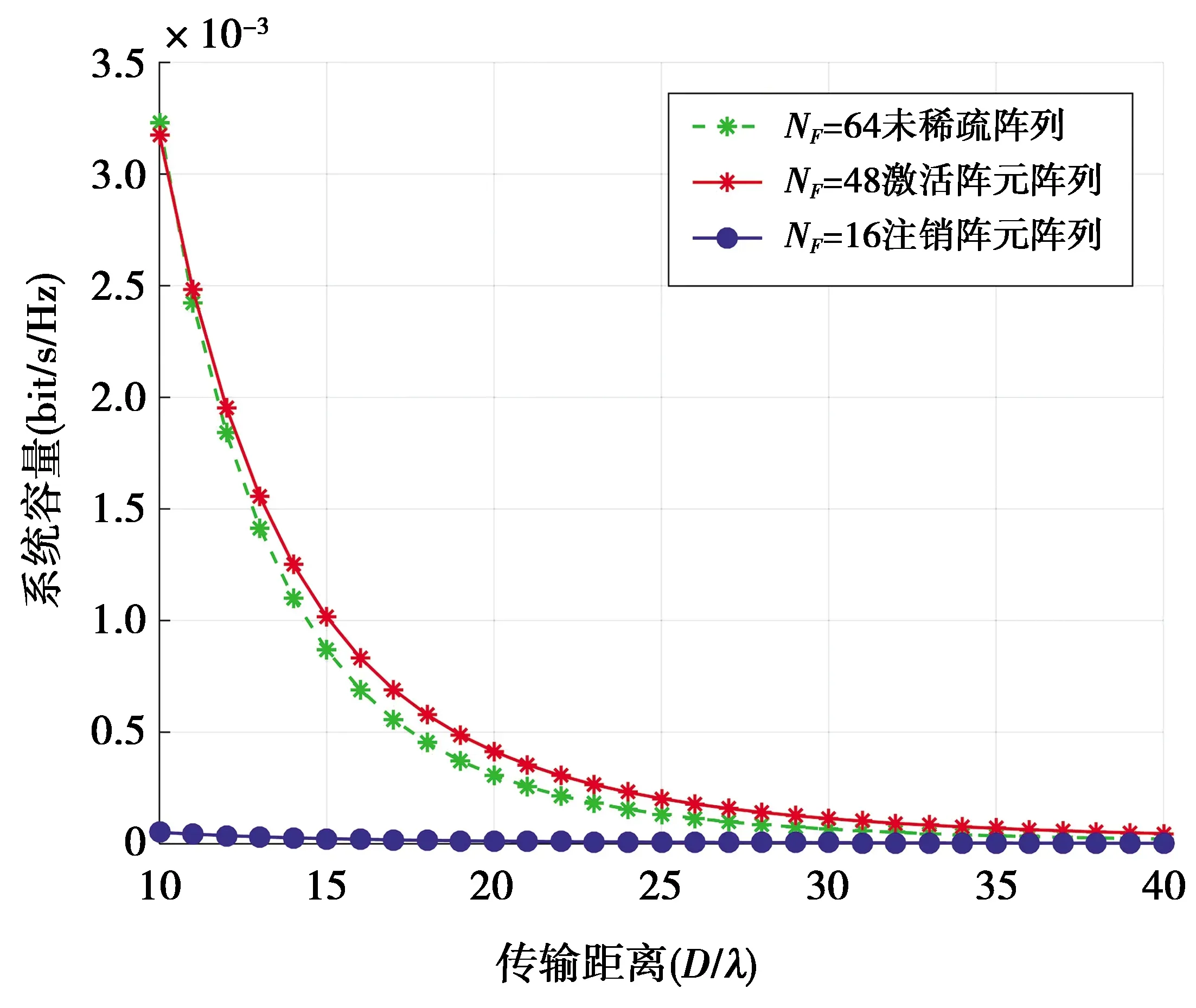
图9 不同发射阵列下相对于传输距离的容量Fig.9 Capacity with respect to the transmission distance considering different SNR

图10展示了不同接收半径下稀疏前后容量差值变化情况。在图10中，稀疏天线数量NF=48，信噪比SNR=30 dB，传输距离D/λ=30，采用图5b的稀疏阵列作为发射阵列。可以看出，随着接收阵列半径的增大，容量差值逐渐减小。主要是因为，稀疏后阵列能使功率向主瓣方向收敛，起到波束赋形的作用。当接收半径增大时，波束赋形效果无法明显地表现出来。

图10 不同接收半径下稀疏后与稀疏前的容量差值Fig.10 Difference of capacity before and after sparsing at different receiving radius

图7—图9表明，与普通平面阵列相比，稀疏矩形阵列能降低SLL，使功率向主瓣方向收敛，且稀疏后的信道容量与稀疏前相比非常逼近。本文方法只对阵列天线进行开关处理，并没有做额外的相位和幅度的“乘法”，所以复杂度和开销都很低。

5 结束语

针对基于矩形阵列MIMO技术不便与UCA-OAM技术相结合，及高模态OAM波大发散性与高衰减的问题，本文给出一种基于矩形阵列OAM波产生方法，并对OAM波进行稀疏优化。结果表明：采用矩形阵列能产生OAM波；在阵列总元素减少约25%的情况下，SRGA方法可以将PSLL降低70%，使功率向主瓣方向收敛，且稀疏前后的信道容量非常逼近。本文方法易于在现代MIMO系统中实现，且在无线通信中具有较大的应用前景。