电力无线专网宏微协同组网中小区协作式故障检测
唐元春
(国网福建省电力有限公司 经济技术研究院,福州 350012)
0 引 言
电力无线专网是专用于承载电力业务的网络,一般由电力公司负责建设和运维管理。电力无线专网是采用广域无线接入技术的数据通信网络系统,为电力系统业务终端与业务主站之间的信息交互提供通信通道服务[1]。为了满足指数增长的电力业务需求,电力无线专网系统将由密集部署的宏微小区组成[2]。然而,对于电力公司来说,电力无线专网宏微协同组网构建的网络(以下简称电力无线宏微网),其维护是当前面临的非常棘手的问题[3-4]。当网络出现故障时,开展抢修工作需要耗费较多的人力和物力,耗时也较长,这极不利于电网的安全运行。为了提高电力无线宏微网的维护效率、降低运维成本、保证电力用户的用电体验,实现网络自愈合势在必行。引入网络自愈合技术旨在让系统在出现故障后,无需人工参与即在短时间内从网络故障中自动恢复。故障检测作为网络性能监督的主体,是实现网络自愈合的首要前提[5-6]。
采用机器学习方法是实现自主高效故障检测的重要途径。为了实现家庭蜂窝网络的自组织管理,文献[7]设计了一种基于协同滤波和序贯假设检验的家庭基站异常检测算法。基于5G网络的高维数据特征,文献[8]提出了一种基于数据降维和模糊分类的小区异常检测机制。文献[9]针对控制面和数据面分离的异构网络场景,提出了基于kNN和灰度预测的两种异常检测方式。然而,现有文献缺乏对电力无线宏微网进行自主联合管理的研究。
在电力无线宏微网中,一个基站的故障可能会影响整个小区的服务性能。因此,对基站进行精确及时的工作状态预测是保证电力用户体验的首要前提。对于电力公司来说,虽然可以获取电力用户测量报告,但基站实际工作状态却难以直接得到。隐马尔可夫模型(hidden Markov models, HMM)是一种根据系统可观测参数推测系统未知信息的有效方法[10]。可以利用HMM方法,根据电力用户测量报告推断基站的工作状态。然而,HMM方法的收敛过程需要消耗较多的时间。通过引入迁移学习(transfer learning, TL)这一概念[11],利用网络已经学习到的知识和宏微网络中相同类型基站间的相似性可以加快HMM的收敛过程。所谓迁移学习,就是将之前任务已经学习到的知识运用到一个全新的相似任务中,使得新任务可以进行更高效的学习[12]。
为了实现电力无线宏微网的自主故障检测,本文提出了一种基于TL算法和HMM算法的小区间协作式工作状态检测算法(以下简称TL-HMM算法),可高效实现小区间协作式工作状态检测,提高小区故障检测精度。
1 系统模型
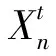
{RSRPn(t),RSRQn(t),RSRPs(t),RSRQs(t)}
(1)
引起基站出现故障的原因有很多,如:硬件故障,软件错误,操作员失误,由电源供应故障造成的外部问题等。为了针对基站的异常程度判定出现故障的原因,本文将基站的工作状态划分为4类,如图1。
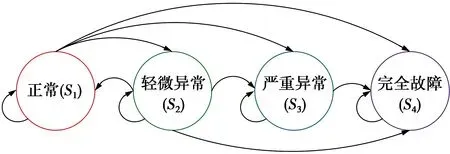
图1 基站工作状态转移图Fig.1 State transition diagram for base stations
S1:正常工作状态。
S2:轻微异常状态,和正常基站差别不大,所以很难检测,一个小区出现轻微异常状态可能由周围的环境因素造成,如气温或气压的变化等。处于轻微异常状态的基站可能在短时间内恢复到正常工作状态,也可能出现服务性能继续恶化的情况。
S3:严重异常状态,处于严重异常状态的小区的业务容量会严重下降。该状态可能由基站的部分软件或者硬件问题造成。当基站处于严重异常状态时,必须采取相应措施进行及时补救,若置之不理则可能转变为完全故障状态。
S4:完全故障状态,处于该状态的基站已经无法自主恢复到正常状态,且已经不具备承载业务的能力,处于该状态的小区需要将与其关联的用户全部卸载到邻小区接受服务。
2 基于TL-HMM的协作式故障检测
对于电力公司来说,当前基站处于哪一种工作状态是难以观测的,但可根据电力用户报告的相关测量数据进行推断和预测。HMM作为一种根据可观测参数推测未知信息的有效方法,可用来解决该问题。
2.1 HMM模型的建立
在HMM模型中,不同的状态之间通过转移概率关联起来,基站的初始状态概率定义了初始时刻各状态的分布情况,如图2所示。对每一个隐藏状态,会遵循观测状态转移概率产生观测数据,这些参数形成了HMM的基本概率矩阵,用λ表示隐马尔科夫模型,则HMM的一般形式为
λ=(D,E,π)
(2)
(2)式中,D为隐藏状态转移概率矩阵;E为观测状态转移概率;π为初始状态概率矩阵。
本文设置基站的状态空间为S={S1,S2,S3,S4},状态总数I的值恒为常数4。观测空间为W={w1,w2,w3,…,wF},其中F表示观测值总数。因此,可将对基站进行故障检测的HMM模型定义为
隐藏状态序列:Q={q1,q2,…,qT},qi∈S;
观测状态序列:O={O1,O2,O3,…,OT},Oi∈W,将每个时刻t的测量数据Xt标记为观测空间中最接近的观测值Ot;
隐藏状态转移概率矩阵:D={dij},dij=P{qt=Sj|qt-1=Si},即某一基站在t-1时刻的工作状态为Si,在t时刻的工作状态为Sj的概率;
观测状态转移概率矩阵:E={ej(wf)},ej(wf)=P(Ot=wf|qt=Sj),表示在t时刻,基站的工作状态为Sj,观测值为wf的概率。
初始状态矩阵:π={πi},πi=P{q1=Si},基站在初始时刻工作状态分别处于Si(i=1,2,3,4)的概率。
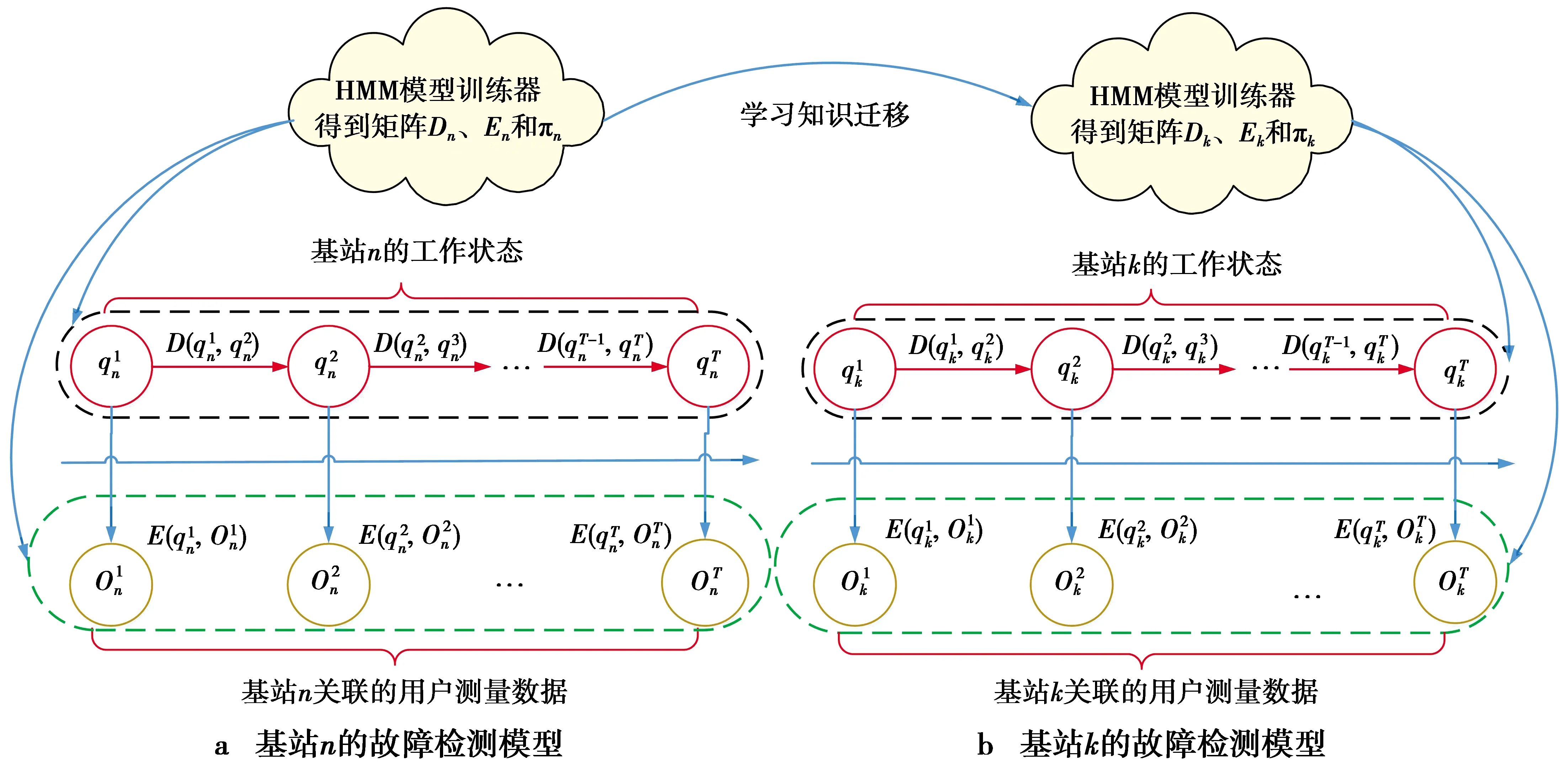
图2 基于TL-HMM的小区间协作式故障检测模型Fig.2 TL-HMM-based cell cooperative anomaly detection
2.2 基站n的工作状态预测过程
t=1,2,3,…,T-1
(3)
(4)
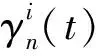
(5)
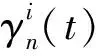
(6)
2.3 HMM参数学习过程
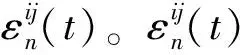
(7)
每一次迭代后都对λn=(Dn,En,πn)各参量进行重新估计,根据Baum-Welch算法[14],重新估计的公式如下
(8)
(9)
(10)
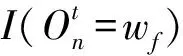
一个基站的观测数据主要由与其关联用户报告的测量数据组成,测量数据包括基站n的RSRP和RSRQ以及最佳邻基站s的RSRP和RSRQ。而产生一个观测序列的概率可作为模型收敛的依据。相关概率估计如下
(11)
可通过(12)式判断模型是否收敛,其中ε为收敛门限值[14]
(12)
上述过程为使用HMM算法进行单个基站工作状态预测的处理方法,为了充分利用网络已学习到的知识,本文将迁移学习的思想用于HMM模型中[11]。因宏微网络中包含大量相同类型的基站,若基站k类型和基站n相似,则可将基站n训练后的参数迁移到基站k中,作为基站k参数更新的部分参考依据,实现相同类型基站间协作式的工作状态预测。
2.4 基于TL-HMM的基站工作状态预测
如图2,当基站n的HMM工作状态预测模型收敛后,可将其相关参数作为历史经验知识,迁移到相同类型的基站k上,加快其训练收敛速度。
基站k的HMM模型的参数更新如下
(13)
(14)
(15)
(15)式中,ζ(t)∈(0,1)为迁移比率。当t→1,ζ(t)→1,也即是说,基站k在开始时根据基站n的HMM模型确定初始参数值;当t逐渐增大时,ζ(t)的值会逐渐减小;而当t→∞时,ζ(t)→0。因此,基站k不仅可以将迁移的知识作为工作状态判定的参考依据,加快收敛速度,还可以在训练过程中逐渐消除外来数据的负面影响[11],本文定义ζ(t)=1/t。基于TL-HMM的基站工作状态预测算法如下。
基于TL-HMM的基站工作状态预测算法

输出:基站k的工作状态
1:在t=0时用基站n的收敛模型对基站k的参数进行初始化
2:do
3:t=t+1
8:得到收敛模型λk=(Dk,Ek,πk)

时间和空间复杂度分析:假设基于HMM和基于TL-HMM的算法收敛所需的迭代次数分别为M1和M2,则它们的时间复杂度分别为O(M1I2T)和O(M2I2T)[15]。基于TL-HMM的故障检测算法可以加快学习进度,故M1>M2,因此,TL-HMM算法的时间复杂度比HMM算法要低。在执行HMM算法和TL-HMM算法时,网络都需要存储长度为T的观测序列,因此,它们的空间复杂度均为O(T)。
3 数值仿真
为了验证协作模式的有效性,本文模拟实用电力无线宏微网运行环境进行仿真。具体仿真参数设置如表1。在仿真过程中,会将基站的传输功率减少δ以模拟基站出现不同程度异常的情况。
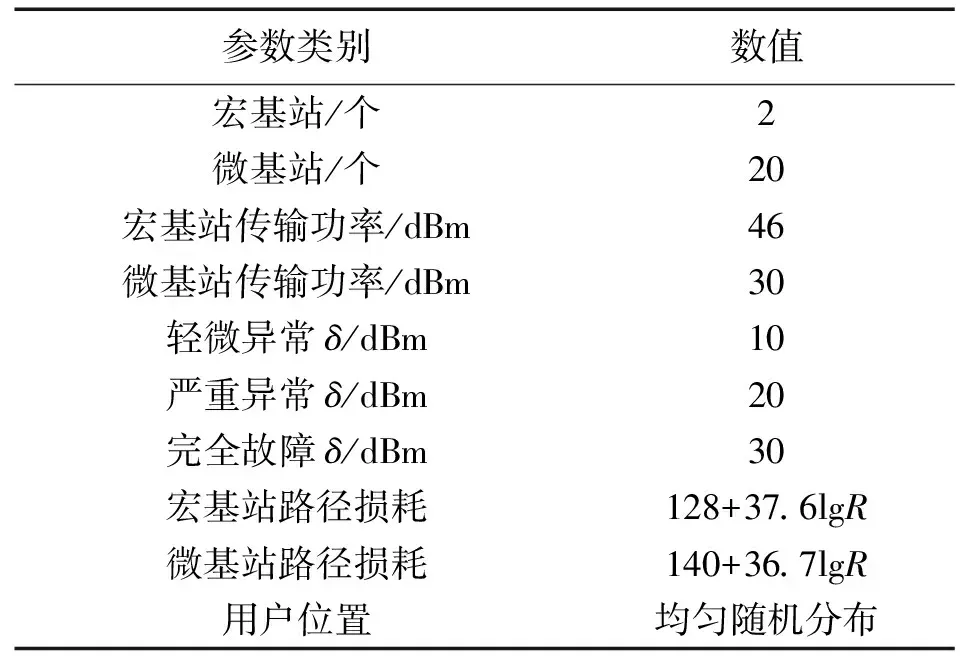
表1 仿真参数Tab.1 Simulation Parameters
图3给出了文献[13]提出的基于HMM的故障检测算法和本文提出算法的性能收敛对比。图3中UD代表100 m×100 m的电力用户密度(User Density),两种算法的收敛门限值ε均设置为10-3[15]。观察图3,对比UD=1和UD=5时算法的检测精确度可知:用户密度较高时,两种算法的检测精确度都相对较高;当用户密度相同时,TL-HMM算法比HMM算法收敛速度更快且可以收敛到更高的精确度。这是因为,TL-HMM算法可以通过迁移学习的方式从一个较优值开始训练参数,从而能够更快收敛到最优性能。

图3 HMM和TL-HMM算法的收敛对比图Fig.3 Convergence comparison between HMM-based and TL-HMM-based algorithms
为了进一步验证TL-HMM算法的检测性能,除了对比HMM算法之外,本文还将其和文献[7]提出的基于协同过滤和序贯假设检测的协作式家庭基站故障检测 (cooperative femtocell outage detection,COD)算法进行了对比,如图4所示。对比中引入了两个统计值:①false positive rate (FPR):FPR用于测量正常状态被错误判断为异常状态的比例;②false negative rate (FNR):FNR用于测量异常状态没有被正确检测出来的比例。由图4可见,FPR和FNR的数值均会随着用户密度的增加逐渐降低,但TL-HMM算法的FPR和FNR的数值均低于HMM算法和COD算法。
通过在宏微网络中调整δ的数值以模拟宏基站和微基站的4种工作状态,图5显示了不同的传输功率和不同的检测方法对4种状态检测精确度的影响。图5中,TL-HMM算法和HMM算法对正常工作状态和完全中断状态的检测精确度均可达到90%以上,而对轻微异常状态的检测精确度最低,这是因为处于轻微异常状态的基站依然可以承载部分业务,故较难准确检测到异常。由于宏基站的传输功率相对于微基站较高,故当基站发生异常情况时,宏基站关联用户产生的测量报告变化也相对较明显,因此,两种算法对宏基站各工作状态的检测精确度都要略高于微基站。此外,如图5,TL-HMM算法的检测性能优于经典HMM算法。

图4 3种故障检测算法在FPR和FNR上的对比图Fig.4 FPR and FNR comparison among three different outage detection algorithms
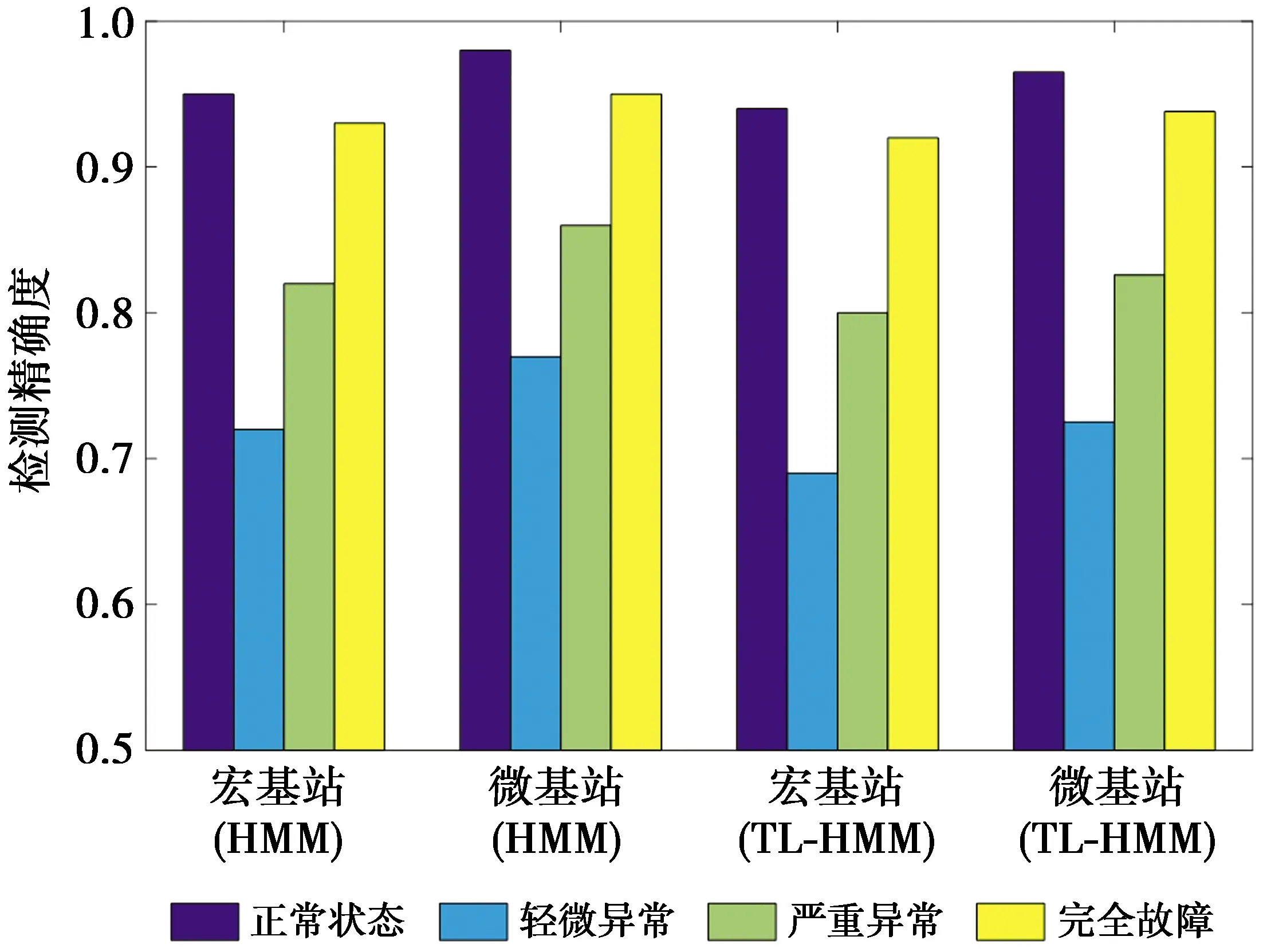
图5 4种基站状态的检测精确度Fig.5 Detection accuracy of four working states of base stations
图6给出了TL-HMM算法中观测序列长度和检测精确度的关系图。本文分别将观测序列长度T设置为观测空间长度F的4、6、8和10倍,从而观察不同观测序列长度对检测精确度产生的影响。如图6,随着观测序列长度的增加,检测精确度也会相应提高,但当观测序列长度增加到观测空间长度的10倍时,其检测精确度几乎和T=8F时相同,因此可知观测序列长度并不是越大越好。
4 结束语
实现对基站工作状态的自主检测是保证电力无线宏微网服务性能的重要前提。仿真结果表明,和传统的HMM算法相比,TL-HMM算法不仅收敛速度快,且检测精度也较高。目前,网络自动化和智能化管理已经成为大势所趋,本文提出的算法可以在网络自动化管理的实现中发挥助推作用。

