基于鲁棒鉴别特征学习的图像特征提取算法
易鹏飞,钟 慧,张召涛,殷家敏,简 鑫
(1.国网重庆市电力公司长寿供电分公司,重庆 401220;2.重庆大学 微电子与通信工程学院,重庆 400044)
0 引 言
图像处理与识别是模式识别和机器学习中最热门的领域之一[1]。然而,通过机器采集的数据往往包含大量的噪声和冗余信息,因此,有必要对图像进行特征提取,以获取图像的紧致特征。特征提取在图像处理的降噪和去冗余中发挥着重要作用[2]。主成分分析(principal component analysis, PCA)[3]和线性判别分析(linear discriminant analysis, LDA)[4]是特征提取的2种经典代表算法,但是这2种方法存在以下2个缺点:①目标函数由二阶统计量(L2范数)构建。众所周知,二阶统计量对异常值和噪声较为敏感[5];②所提取的特征是所有原始特征的线性组合,难以有效区分有用信息与无用信息。
针对以上2个问题,学者们提出了很多针对性的改进算法[6]。其中联合二阶统计量和一阶统计量(L2,1范数)的方法不仅因其融合了一阶统计量能够稀疏样本的优点,而且还能够有效地区分有用信息与无用信息,从而受到了学者们的关注[7]。例如:Nie等[8]在提出鲁棒特征选择的同时引入了L2,1范数作为正则化项,增强了算法的鲁棒性和联合稀疏性。Yi等[9]提出了联合稀疏主成分分析以共同选择有用特征并增强对异常值的鲁棒性。Huang等[10]提出了一种基于L2,1范数的稀疏子空间学习方法——判别稀疏张量邻域保留嵌入算法,能够很好地对图像特征稀疏的同时实现特征信息的鉴别区分,进而实现高的分类精度。Han等[11]提出了一种新的基于小波变换的多频带联合局部稀疏跟踪算法,实现了图像特征稀疏以及信息鉴别。
综上所述,利用L2,1范数定义的特征学习模型不仅可以减轻异常值和噪声对模型影响,还可以提高模型对特征信息的鉴别能力,因而被广泛用于特征提取。但是,这些方法对于损坏较为严重的图像识别效果依然不够理想。因此,为了进一步减轻损坏图片(强噪声和异常值)的影响,提取出更加具有鉴别力的特征,增强模型的鲁棒性和提高图像的识别率。本文提出模型在利用L2,1范数最大化准则定义特征学习模型的同时,还对模型做了以下的改进。首先,对类内的样本进行聚拢处理,使得同类样本尽量靠近类中心;然后,为减少类内损坏严重的样本对识别效果的影响,对类内聚拢后的样本再次进行筛选;最后,利用L2,1范数重新定义了数据的类内和类间相关矩阵,同时引入加权参数避免样本类中心距离过远或过近的情况。
1 系统模型
1.1 类内聚拢
为了减轻不同类别但却较为相似的图像对算法性能造成影响,对图像进行聚拢操作就显得尤为重要。聚拢即是希望尺度变换后的同类样本尽量靠近样本类中心。具体步骤如下。
首先,求解每类样本的样本中心
(1)
然后,按余弦相似性计算每一样本与其对应的样本类中心的相似性
(2)
最后,对每一样本赋予相似度权值,得到处理后的新样本
(3)
1.2 提出算法——鲁棒鉴别特征学习
如前文所述,L2,1范数定义的特征学习模型不仅可以减轻异常值和噪声对模型的影响,还可以提高模型对特征信息的鉴别能力。因此,提出了一种基于L2,1范数的改进型LDA算法,提升了模型的信息鉴别能力和鲁棒性。
1.2.1 定义相关数据矩阵
算法需要对一些相关数据矩阵进行重新定义,其定义方法和步骤如下。
1)类内相关数据矩阵的定义。利用L2,1范数的思想,构建类内对角矩阵Dwithin,并且引入筛选数据的因子α,剔除样本中的一部分异常样本。类内相关矩阵Xwithin和类内对角矩阵Dwithin构建为
(4)
(5)

2)类间相关数据矩阵的定义。利用样本类中心构建数据矩阵,并且引入加权参数pi,j,避免样本中心之间距离过大或过小。类间相关矩阵Xbetween和类间对角矩阵Dbetween构建为
(6)
(Dbetween)ii=
(7)

为了得到联合稀疏投影,利用L2,1范数思想构建投影对角矩阵DB为
(8)
根据LDA最大化类间散度矩阵,最小化类内散度矩阵,同时加入L2,1范数联合稀疏的思想,提出算法的目标函数为
(9)
(9)式中:ε为惩罚因子;cons为一个常数。
1.2.2 模型求解方法
tr(BTSwithinB)
(10)
然后,对目标函数的第二项ε·‖B‖2,1按序展开并采用(8)式化简可得
ε·‖B‖2,1=ε·tr(BTDBB)
(11)
最后,根据(6)式和(7)式对约束项进行化简转化可得
tr(BTSbetweenB)
(12)
综上所述,提出算法的目标函数可以重写为
s.t. tr(BTSbetweenB)=cons
(13)
类似于LDA的求解方法,将(13)式转化为求迹问题
(14)
根据拉格朗日乘子法可得其广义特征值函数
(Sbetween)-1(Swithin+ε·DB)B=BΛ
(15)
对角矩阵Λ由其对应的特征向量的特征值组成,其对应的特征向量位于投影矩阵B的每一列中。因此,通过矩阵(Sbetween)-1(Swithin+ε·DB)的特征分解来解决最小化问题,并且最优矩阵B由其最小特征值所对应的特征向量组成。由于Dwithin,DB和Dbetween的更新与上一次迭代获得的投影矩阵B有关,因此,可采用交替方向乘子法求解最佳投影矩阵B。
基于如上描述,提出算法的求解步骤如算法1。
算法1鲁棒鉴别特征学习算法
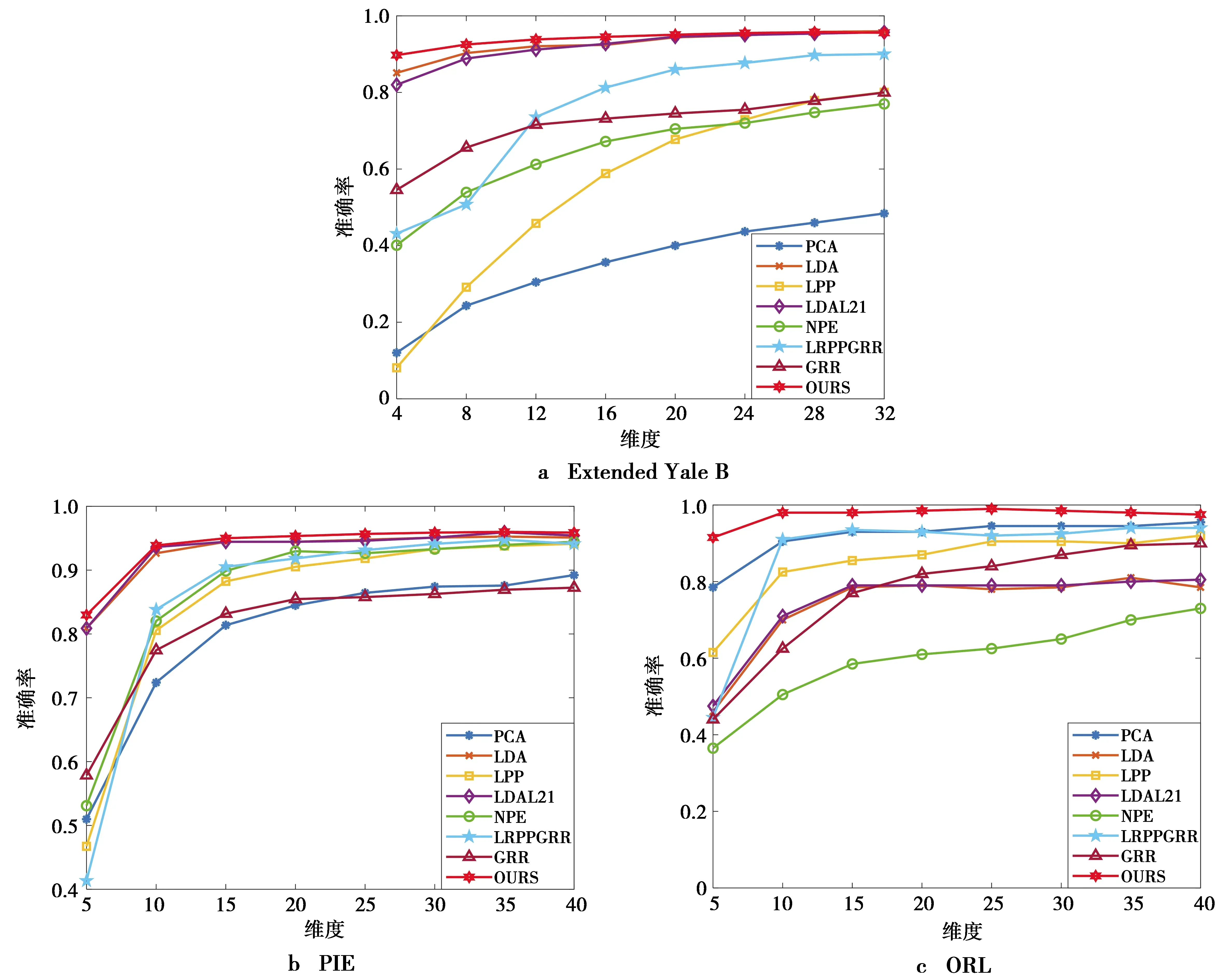
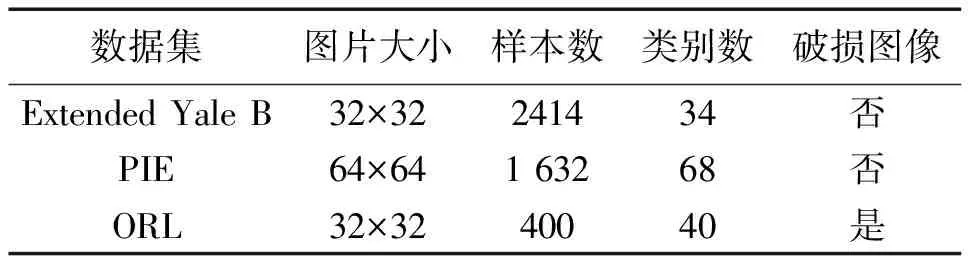
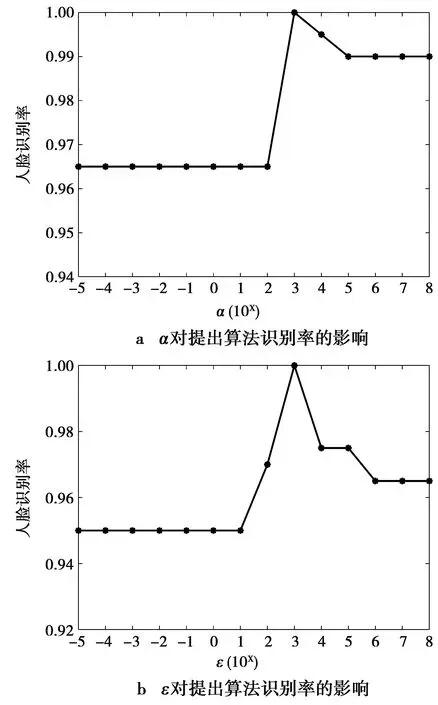
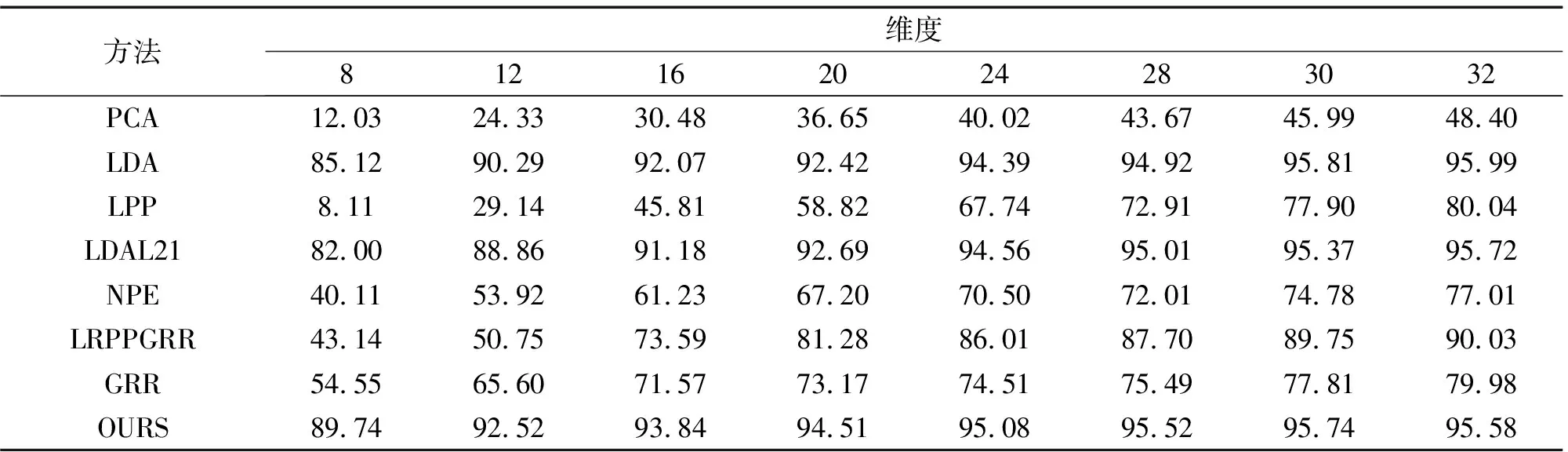
输入 数据矩阵Xn×d,最大迭代次数ite,维数k( 输出 投影到低维空间yi=xiB(i=1,2,3,…,n)。 1.分别用(4)式、(6)式构建矩阵Xwithin、Xbetween 2.初始化矩阵B∈Rn×k 3.当t=1:ite 4.求解特征值分解问题得到B 5.用(5)式更新Dwithin 6.用(7)式更新Dbetween 7.用(8)式更新DB 8.t=t+1 9.函数收敛或达到最大迭代次数,退出循环 10.输出最优投影矩阵B 11.训练样本投影到低维空间yi=xiB(i=1,2,3,…,n) 引理1对于任何非零向量u,ut∈Rn有 (16) 证明:设bi表示B的第i行数据,则第t+1次迭代可以得到 (17) (18) 由(18)式可得 (19) 根据(16)式可得 (20) 由(19)式和(20)式可得 (21) ‖Bt+1‖2,1≤‖Bt‖2,1 (22) 由(21)式和(22)式可得 (23) 最终提出算法的目标函数可表示为 (24) 为了验证提出算法的有效性,采用3个图像识别数据集评估提出算法的性能。同时,采用多个与提出算法同类型的图像识别算法进行对比,以验证提出算法的先进性。 本文采用了3个广泛使用的图像数据集,这3个数据集分别是Extended Yale B数据集、PIE数据集和ORL数据集。数据集按照文献[12]进行了裁剪操作,Extended Yale B数据集和ORL数据集中的图片被裁剪为32×32大小,PIE数据集中的图片被裁剪为64×64大小。需要特别说明的是,为了验证提出算法在破损图像数据集上的性能,在ORL数据集上叠加了高斯强噪声以模拟破损图像。表1记录了本文所用数据集的基本信息。 表1 数据集基本信息Tab.1 Basic information of the datasets 实验在每类数据中随机选择q幅图像组成训练样本,剩余全部图像作为测试样本。在Extended Yale B数据集中,设置q=32;PIE数据集,设置q=15;ORL数据集,设置q=5。每个实验重复10次并取10次结果的平均值作为算法的性能指标以消除偶然性对实验结果的影响。在实验中,为了消除散度矩阵求逆运算引起的奇异值问题,在进行实验之前,使用PCA对数据进行了预处理。分类器采用的是K-最近邻(K-nearest neighbors,KNN)(K=1)。实验在Windows10下的MATLAB R2020a软件平台上进行。 提出算法包含2个参数:ε和α。为确定最优参数,对ε和α在[10-5,10-4,…,108]进行了寻优操作。图1显示了ORL数据集下识别率随ε和α的变化情况。从图1可以看出,当ε和α设置为ε=103,α=103时,提出算法性能最佳。同理可得,Extended Yale B的参数设置为ε=102,α=103;PIE的参数设置ε=103,α=103。 图1 参数对提出算法识别率的影响Fig.1 Influence of parameters on the recognition rate of the proposed algorithm 确定提出算法的参数后,接下来将我们提出的算法(our proposed method, OURS)与一些经典或者最新的图像识别算法进行对比。这些算法包括:LDA[4],局部保持投影(locality preserving projections, LPP)[13],近邻保持嵌入(neighborhood preserving embedding, NPE)[14],带L2,1范数的LDA(LDA with L2,1norm, LDAL21)[12],图正则化重建低秩保留投影(low-rank preserving projection via graph regularized reconstruction, LRPPGRR)[15],广义鲁棒回归(generalized robust regression, GRR)[16]。表2—表4分别记录了Extended Yale B,PIE和ORL 3个图像数据集的不同算法在不同特征维度下(经过PCA预处理之后的维度)的识别率。需要特别说明的是,对比算法均进行了参数寻优操作。 表2 算法在不同维度下的识别率(Extended Yale B, %)Tab.2 Recognition rate of algorithms in different dimensions on Extended Yale B (%) 表3 算法在不同维度下的识别率(PIE, %)Tab.3 Recognition rate of algorithms in different dimensions on PIE (%) 表4 算法在不同维度下的识别率(ORL, %)Tab.4 Recognition rate of different algorithms in different dimensions on ORL (%) 从表2可以看出,在Extended Yale B数据集中,提出方法在大多数情况下(6/8)总是优于其他算法,最高识别率可达到95.74%。从表3可以看出,在PIE数据集上,提出算法在不同维度下总是(8/8)优于其他对比算法,最高识别率可高达96%。从表4可以看出,在破损图像集ORL数据集上,提出算法在不同维度下总能取得最高分类识别率,且分类识别率较现有算法优势较为明显。综上所述,提出算法相比于现有的同类型图像识别算法,无论是在一般图像数据集上,还是在破损数据集上都具有更高的识别率。 前文已经对论文的参数ε和α进行了设置和分析,但维度依然是模型的一个重要参数。因此,这部分内容将讨论OURS随维度的变化情况。公平起见,所有算法都采用经过PCA预处理后,维度为40的情况下的数据。图2记录了不同算法的识别率随特征维度的变化情况。从图2中可以看出,所有算法的识别率先随着维度的增加而增加,然后趋于稳定。当维度为10时,提出算法已经收敛,这明显优于其余对比算法。 本文为了获取图像的紧致特征表示,同时减小噪声以及异常值对算法性能的影响,提出了一种用于图像特征提取的鲁棒鉴别特征学习算法。首先,采用类内聚拢有效地减少了样本的误判率;其次,提出了一种新型的L2,1范数准则对模型进行联合稀疏重建,使模型具有更强的鲁棒性和鉴别有用与无用特征的能力;最后,在3个公开图像数据集上进行了实验,并与多个与提出算法同类型的图像识别算法进行对比。实验结果证明了提出算法的有效性和鲁棒性。 图2 不同算法的识别率随维度的变化曲线Fig.2 Variation curve of the recognition rate of different algorithms with the dimension2 收敛性分析
3 实验验证
3.1 数据集
3.2 实验设置
3.3 参数设置
3.4 实验结果与分析


3.5 参数分析
4 结 论