PLDPC码的相关信源联合译码系统设计与分析
肖 旻,高 天
(厦门理工学院 光电与通信工程学院,厦门 361005)
0 引 言
无线传感器网络包含许多分布在环境中用于收集信息的传感器,这些传感器收集环境信息,编码后再发送数据,由一个中央处理器接收信息并进行集中处理。大多数情况下,传感器之间的距离越近,接收到的信息越相似。相关信源的信源/信道联合编译码已在多种传输场合被广泛研究[1-5]。相关信源联合译码系统,通过利用相关信源之间的相似信息,不仅能维持低误码率,还能降低传感器功耗、延长传感器使用寿命。文献[6]提出了基于LDPC码的相关信源联合译码(joint decoding of correlated sources based on LDPC codes,JDCS-LDPC)系统,文献[7]通过改进外信息转移(extrinsic information transfer,EXIT)图,对JDCS-LDPC系统性能进行分析,设计出度分布适合JDCS-LDPC系统的LDPC码。
原模图LDPC(protograph low density parity check, PLDPC)码,由美国喷气推进实验室提出,具有结构化的特点,近几年得到了广泛重视,现已被应用在深空通信、磁记录系统等领域[8-9]。PLDPC码既继承了LDPC码优异的纠错能力,又可以轻松实现各种码率扩展且编译码复杂度低,因此非常适用于一些自动反馈重传的通信系统,可以根据信道的质量改变传输码率,适合作为无线传感网络中信道编码的参考。
本文将PLDPC码应用在相关信源的联合译码框架下,组成基于PLDPC码的相关信源联合译码(joint decoding of correlated sources based on PLDPC codes,JDCS-PLDPC)系统,并分析其性能。由于EXIT图和基于原模图的外信息转移(protograph-based EXIT,PEXIT)算法均不能直接分析PLDPC码在JDCS系统下的门限值,因此,本文在PEXIT算法的基础上提出了适合JDCS系统的原模图外信息转移(JDCS-PEXIT)算法,通过该算法对JDCS-PLDPC系统的门限值进行分析,并通过性能仿真验证了该分析算法的有效性。
1 JDCS-PLDPC系统
1.1 原模图的基本概念
原模图(protograph)通常可以表示为G=(V,C,E),其中,V为变量点集合、C为校验点集合、E为连接变量点和校验点的边集合。在原模图中允许度为1的变量点和重边存在;同时允许引入删余(punctured)变量点,这种变量点对应的消息符号不发送到信道中,即在译码时这些变量点没有信道初始信息。原模图对应的校验矩阵称为基础矩阵B,B中第i行、第j列的元素bi,j表示第i个变量点vi与第j个校验点cj之间所连接的边数。PLDPC码的因子图则是由原模图经过“复制-置换”(copy-and-permute)得到。PLDPC码的性能由其基础矩阵和扩展规则决定,本文使用的扩展规则为改进型PEG(modified progressive edge-growth,MPEG)算法[10]。
1.2 JDCS-PLDPC系统框架


图1 JDCS系统框图Fig.1 Block diagram ofthe JDCS system
JDCS-PLDPC系统的联合译码结构见图2,完成一次译码需要经过全局迭代和子译码器的本地迭代,一次全局迭代中包含多次的本地迭代,JDCS-PLDPC系统译码算法步骤如下。


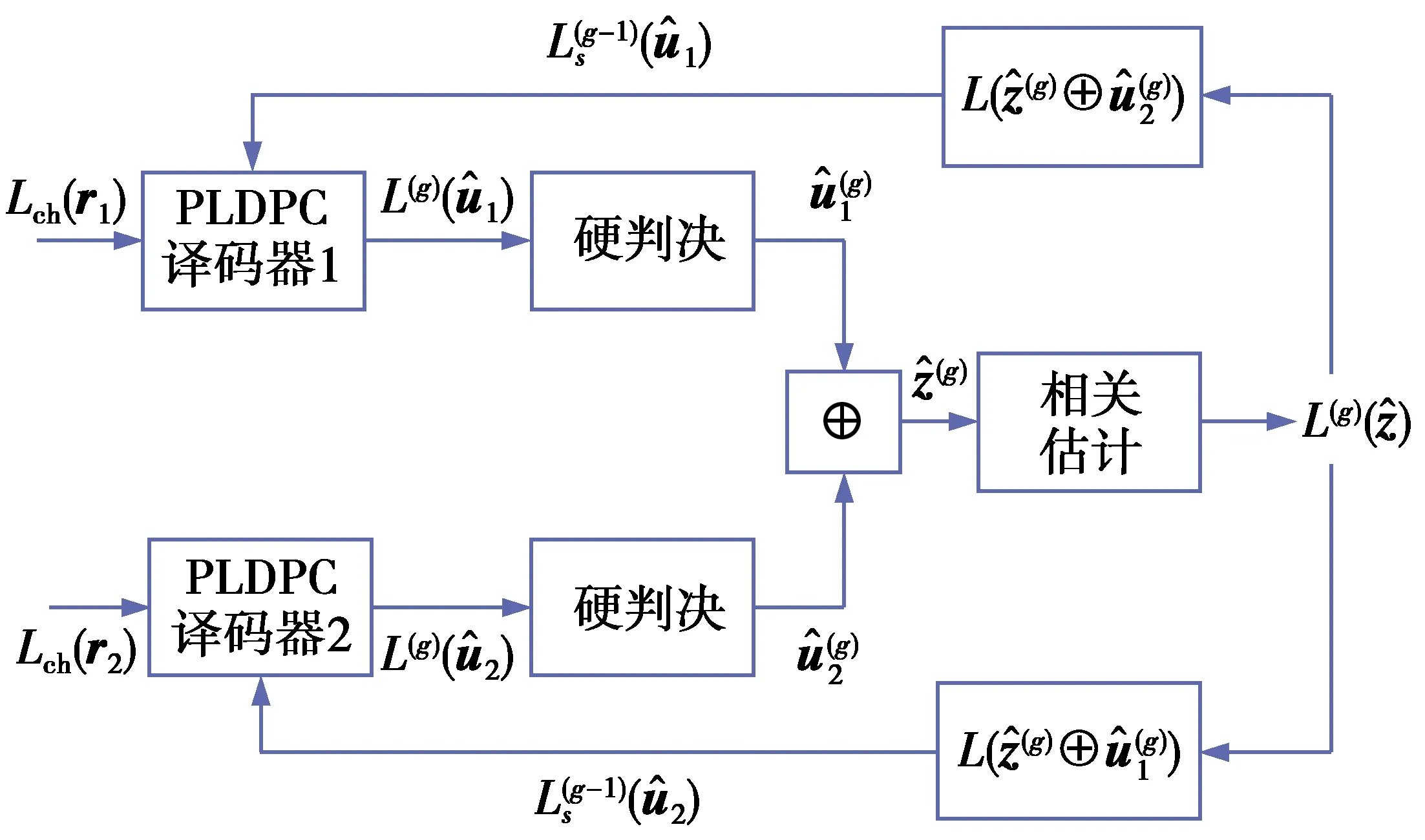
图2 JDCS-PLDPC系统中的联合译码结构Fig.2 Block diagram ofjoint decoding in the JDCS-PLDPC system

(1)


步骤5当到达设定的最大全局迭代次数gmax次时,输出译码结果,否则返回步骤2。
2 JDCS-PLDPC系统的PEXIT分析
与传统LDPC码类似,PLDPC码也可以通过分析门限值Th来预测其纠错性能。只要传输信噪比SNR≥Th,随着分组长度和迭代译码次数的增加,该码可以达到任意小的误比特率。文献[11]采用EXIT算法来分析传统LDPC码的门限值,但EXIT算法无法处理PLDPC码特有的删余变量点和度为1的变量点,也无法分析原模图中边连接关系带来的性能差异。因此,文献[12-13]针对PLDPC码提出PEXIT算法分析其门限值。本文研究的JDCS系统针对两个相似信源进行联合译码,而传统PEXIT算法仅能分析单个信源BP译码性能,无法计算相关信源联合译码中两个子译码器之间所传递的外信息,不适用于JDCS系统。基于此,本文在PEXIT算法的基础上提出了JDCS-PEXIT算法,以此分析JDCS系统中PLDPC码的门限值。
2.1 JDCS-PLDPC系统中的信息转移
为了分析JDCS-PLDPC系统下PLDPC码的门限值,需要跟踪联合译码里全局迭代和本地迭代中信息的转移。图3显示了JDCS-PLDPC系统中的信息转移过程。

图3 JDCS-PLDPC系统中的信息转移图Fig.3 Information transfer graph of the JDCS-PLDPC system
根据前述的联合译码结构,全局迭代输出的外部信息仅作用于信息序列的信源比特,因此,变量点可以分为2种:①信息位对应的变量点,简称信息变量点,既有信道初始信息,又接收全局迭代提供的外部互信息,这些变量点所在的集合用Vs表示;②冗余位对应的变量点,简称冗余变量点,仅接收信道初始信息,这些变量点所在的集合用Vr表示,该集合中包含删余位,删余位变量点的信道初始信息为0。
校验点向信息变量点和冗余变量点发送的外部互信息计算方式不同,因此,需要将外部互信息分为2类:向信息变量点发送的外部互信息和向冗余变量点发送的外部互信息。
状态点通过分析相关信源的相似程度,在全局迭代中将一个子译码器信息变量点的后验互信息转化为外部互信息,输出到另一子译码器的信息变量点。
根据以上分析,可以定义6类互信息(mutual information, MI)。
第1类,变量点从校验点接收的先验MI。
•IAvs(i,j),表示从校验点ci输入到信息变量点vj(vj∈Vs)的LLR与第j个编码比特之间的先验MI;
•IAvr(i,j),表示从校验点ci输入到冗余变量点vj(vj∈Vr)的LLR与第j个编码比特之间的先验MI;
第2类,校验点从变量点接收的先验MI。
•IAcs(i,j),表示从信息变量点vj(vj∈Vs)输入到校验点ci的LLR与第j个编码比特之间的先验MI;
•IAcr(i,j),表示从冗余变量点vj(vj∈Vr)输入到校验点ci的LLR与第j个编码比特之间的先验MI。
第3类,变量点发送给校验点的外部MI。
•IEvs(i,j),表示信息变量点vj(vj∈Vs)输出给校验点ci的LLR与第j个编码比特之间的外部MI;
•IEvr(i,j),表示冗余变量点vj(vj∈Vr)输出给校验点ci的LLR与第j个编码比特之间的外部MI。
第4类,校验点发送给变量点的外部MI。
•IEcs(i,j),表示校验点ci输出给信息变量点vj(vj∈Vs)的LLR与第j个编码比特之间的外部MI;
•IEcr(i,j),表示校验点ci输出给冗余变量点vj(vj∈Vr)的LLR与第j个编码比特之间的外部MI。
第5类,变量点的后验MI。
•Iapps(j),表示信息变量点vj(vj∈Vs)的后验LLR与第j个编码比特之间的后验MI;
•Iappr(j),表示冗余变量点vj(vj∈Vr)的后验LLR与第j个编码比特之间的后验概率MI。
第6类,全局迭代输入到信息变量点的外部MI。
•Ih(j),表示状态点输出给子译码器的第j个信息变量点vj(vj∈Vs)的外部MI。
由以上互信息的定义可以得到如下等式。
IAvs(i,j)=IEcs(i,j)
IAvr(i,j)=IEcr(i,j)
IEvs(i,j)=IAcs(i,j)
IEvr(i,j)=IAcr(i,j)
2.2 JDCS-PEXIT算法
为了分析JDCS-PLDPC系统下PLDPC码的门限值,需要对JDCS-PLDPC系统中联合译码的信息转移进行分析,具体的外部互信息转移可以参考图3所示的信息转移图。
JDCS-PEXIT算法步骤如下。
步骤1初始化。设置初始信噪比为Th0,针对m×n的原模图基础矩阵设置如下。
令j∈{1,2,…,n-m},全局迭代输出给信息变量点vj(vj∈Vs)的外部互信息Ih(j)=0。
令i∈{1,2,…,m},j∈{1,2,…,n-m},校验点ci输出给信息变量点vj(vj∈Vs)的外部互信息IEcs(i,j)=0。
令i∈{1,2,…,m},j∈{1,2,…,m},校验点ci输出给冗余变量点vj(vj∈Vr)的外部互信息IEcr(i,j)=0。
步骤2对所有j∈{1,2,…,n},计算变量点vj的AWGN信道初始信息的方差[9]。
(4)
步骤3计算变量点输出给校验点的外部MI。
1)对所有i∈{1,2,…,m},j∈{1,2,…,n-m}计算第t次本地迭代中,信息变量点vj(vj∈Vs)输出到校验点ci的外部互信息IEvs(i,j)。
(5)
(5)式中:Φ(bi,j)的定义为

(6)

(7)
2)对所有i∈{1,2,…,m},j∈{1,2,…,m},计算第t次本地迭代中,冗余变量点vj(vj∈Vr)输出到校验点ci的外部互信息IEvr(i,j)。
(8)
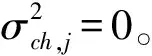
步骤4计算校验点输出给变量点的外部MI。
对所有i∈{1,2,…,m},计算第t次本地迭代校验点ci发送给信息变量点vj(vj∈Vs)和冗余变量点vj(vj∈Vr)的两种外部互信息IEcs(i,j)和IEcr(i,j)。
(9)
(10)
步骤5计算所有变量点的后验MI。

(11)

(12)
步骤6若满足
(13)
则跳转至步骤8,否则,令t=t+1,返回步骤3,继续本地迭代;若达到最大本地迭代次数T仍不能满足上述条件,则进入步骤7。
步骤7令全局迭代次数g=g+1,返回步骤3。若当g=gmax时,仍不满足(13)式,则在本次全局迭代的信噪比基础上增加ΔdB,跳转至步骤2开始下次全局迭代。
步骤8输出此时的信噪比Eb/N0,作为JDCS-PLDPC系统中的PLDPC码在AWGN信道下的译码门限值Th。
3 JDCS-PLDPC系统性能分析与仿真
3.1 JDCS-PLDPC系统性能分析
本文采用JDCS-PEXIT算法,分析了AR3A和AR4JA这两类常用PLDPC码在相关信源联合译码系统中的性能。根据文献[6],在给定码率的情况下,相关信源实现无差错传输的条件为
(14)
(14)式中:Rc为JDCS-PLDPC系统码率;H(u1,u2)为两个相关信源序列的联合熵;N0表示单边功率谱密度;Eso表示每个信源比特产生的能量, 2Eso=H(u1,u2)Eb[15-16]。
信源相关度p=0.95时,可得出表1数据。从表1可见,在不同码率下,AR3A码和AR4JA码的译码门限距离理论极限仍有2~3 dB的差距,表明PLDPC码在JDCS系统中具有一定的优化空间。在优化时,JDCS-PEXIT算法可以作为有力的工具帮助设计和分析各种PLDPC码在JDCS系统下的性能。
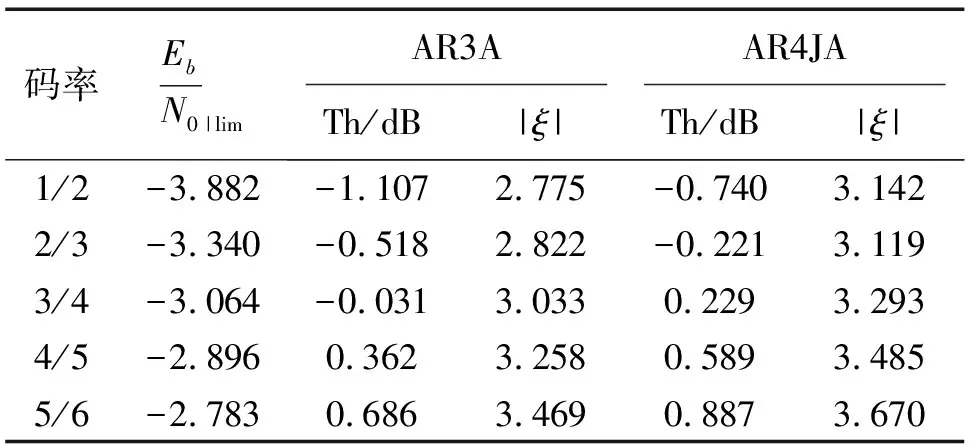
表1 JDCS-PLDPC系统下AR3A码和AR4JA码门限值Tab.1 Thresholds of AR3A and AR4JA codes in the JDCS-PLDPC system
信源相关度变化时,可得表2数据。从表2可以看出,随着相关度的提高,JDCS-PLDPC系统比传统BP译码的增益更大。

表2 1/2码率下AR3A码和AR4JA码在JDCS-PLDPC 系统和传统BP译码中的门限值对比Tab.2 Threshold comparison between the JDCS-PLDPC system and the traditional BP system with rate-1/2 AR3A and AR4JA codes
3.2 JDCS-PLDPC系统性能仿真
为验证本文所提JDCS-PEXIT算法的有效性,对JDCS-PLDPC系统在各种不同条件下进行仿真分析,设定帧长为2 048,最大全局迭代次数为5,最大本地迭代次数为30。
1)设信源相关度为p=0.95,仿真对比码率为1/2和3/4时,JDCS-PLDPC译码和传统BP译码下,AR3A码和AR4JA码的误码率性能。为了方便表示,将引入这两类PLDPC码的JDCS系统分别称为JDCS-AR3A和JDCS-AR4JA。
在1/2码率情况下,仿真结果见图4。JDCS-AR3A系统和JDCS-AR4JA系统分别优于传统BP译码约1.6 dB和1.2 dB。传统BP译码中的AR3A码和AR4JA码在1/2码率下的门限值分别为0.482 dB和0.625 dB[17],与JDCS-AR3A和JDCS-AR4JA系统门限值的差距分别为1.589 dB和1.365 dB,这一差距与仿真结果基本一致。

图4 1/2码率下JDCS-PLDPC译码和传统 BP译码性能对比Fig.4 Performance comparison between the JDCS-PLDPC system and the traditional BP system with rate-1/2 AR3A and AR4JA codes
在3/4码率情况下,仿真结果见图5。 JDCS-AR3A系统和JDCS-AR4JA系统分别优于传统BP译码约1.8 dB和1.7 dB。传统BP译码中的AR3A码和AR4JA码在3/4码率下的门限值分别为1.850 dB和2.004 dB[17],与JDCS-AR3A和JDCS-AR4JA系统门限值的差距分别1.881 dB和1.775 dB,同样与仿真结果基本一致,表明本文所研究的JDCS-PEXIT算法具有预测JDCS-PLDPC系统性能的作用。
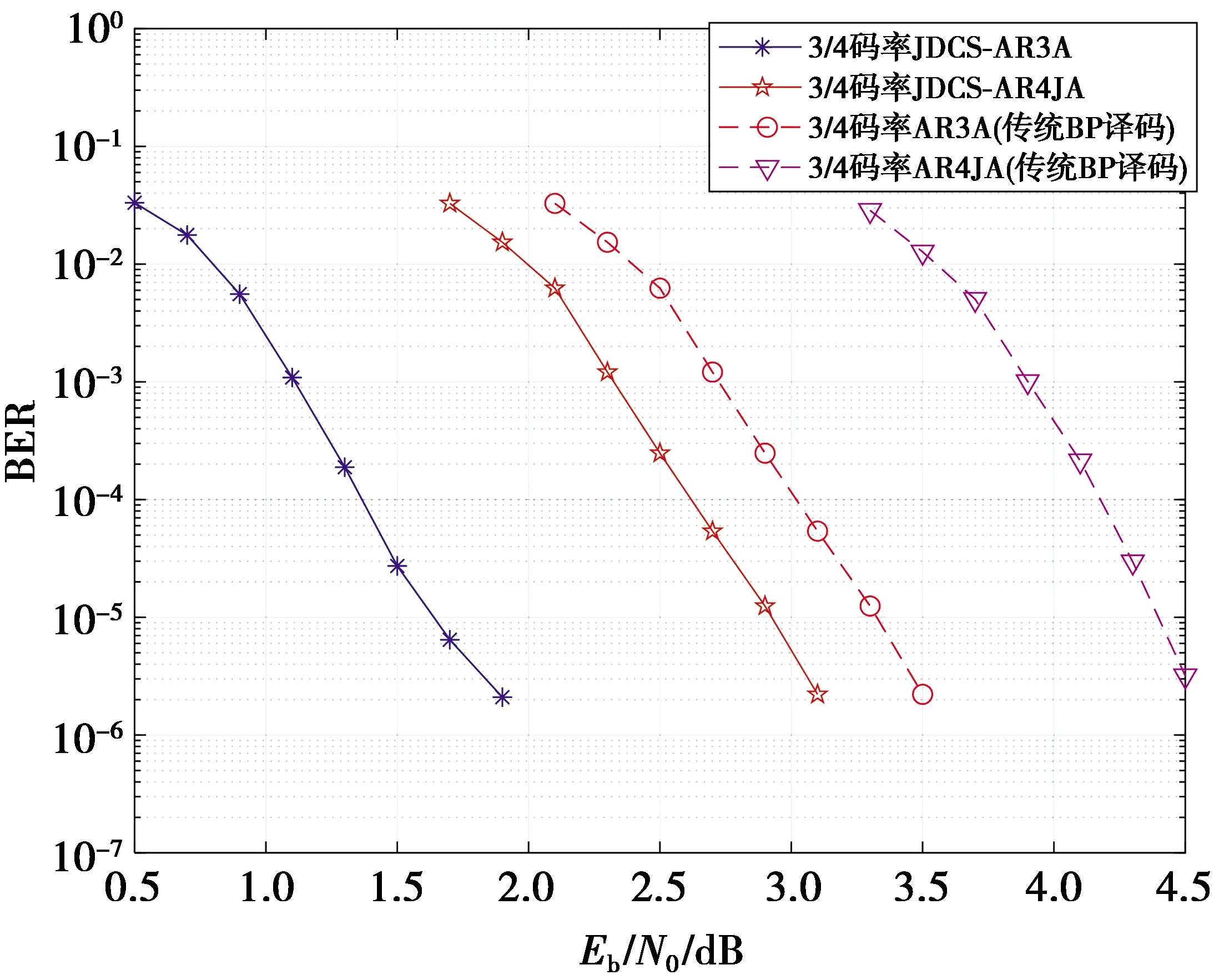
图5 3/4码率下JDCS-PLDPC译码和传统 BP译码性能对比Fig.5 Performance comparison between the JDCS-PLDPC system and the traditional BP system with rate-3/4 AR3A and AR4JA codes
2)采用AR4JA码对比不同相关度下JDCS-PLDPC系统的性能。图6展示了信源相关度为0.95、0.9和0.85情况下,JDCS-PLDPC系统性能仿真结果。从图6可以看出,随着信源相关度的提高,JDCS-AR4JA系统较传统BP译码的优势进一步扩大。这与3.1节中利用JDCS-PEXIT算法分析的结果一致。

图6 JDCS-PLDPC系统在不同信源相关度下的仿真性能Fig.6 Performances of the JDCS-PLDPC system with different source correlation coefficients
3.3 复杂度分析
对于JDCS-PLDPC系统,一次全局迭代的复杂度主要分为两个部分:本地迭代的复杂度和全局迭代中子译码器间传递外信息的计算复杂度。由于本地迭代采用传统BP译码,因此,JDCS-PLDPC系统较传统BP译码所增加的复杂度来自全局迭代中外信息的计算,即(1)式和(2)式。 (2)式通常被称为“田”字运算,一般通过查表的方式获得结果。
信息序列长度为k时,一次全局迭代中JDCS-PLDPC系统较传统BP译码所增加的复杂度如表3所示。从表3可知,在一次全局迭代中,相比BP译码,JDCS-PLDPC系统增加的操作主要是简单的加法和查表运算,且增加的运算次数与信息序列长度k呈线性关系,相对复杂的除法与对数运算仅增加一次。同时通过仿真发现JDCS-PLDPC系统迭代译码收敛时需要的全局迭代次数一般为3—5次。因此,在实际应用时,JDCS-PLDPC系统相比传统BP译码所增加的复杂度并不大。
4 结束语
针对两个相关信源的信息传输问题,本文在构建JDCS-PLDPC系统的基础上,提出了分析系统译码门限值的JDCS-PEXIT算法,并利用该算法对JDCS-PLDPC系统进行性能分析。仿真结果与JDCS-PEXIT算法分析结果基本一致,验证了该算法的有效性。JDCS-PLDPC系统复杂度分析表明,相比于传统BP译码,JDCS-PLDPC系统在全局迭代中增加的操作主要是简单的加法和查表运算,且运算量与信息序列长度呈线性关系。

表3 一次全局迭代中JDCS-PLDPC系统 相比传统BP译码增加的复杂度Tab.3 Added complexity of JDCS-PLDPC system compared with traditional BP system in one global iteration

