多归一化因子的LDPC译码算法
陈发堂,王永航,张翰卿
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
1962年,文献[1]首次验证了低密度奇偶校验(low density parity check, LDPC)码优越的性能,但由于当时技术不够完善,在接下来的几十年里并没有引起大量关注。文献[2]重新研究了LDPC码,证明其译码性能很接近香农限。2016年,QC-LDPC(quasi-cyclic LDPC)[3]因其良好的性能成为5G 新空口一种主要的信道编码方案[4]。
LDPC码的译码方法都以置信(belief propagation, BP)算法为基础[5-6]。其中最小和(min-sum, MS)算法是BP算法简化后的译码方式,只需要加法和比较就可以完成译码,但牺牲了一部分译码性能[7]。为弥补MS算法损失的性能,文献[8]提出归一化最小和(normalized min-sum, NMS)算法,可以提供更加接近BP算法的译码性能。文献[9]利用权值将前5次迭代的归一化因子α整合为一个值,使LDPC误码率再次降低。对于不满足校验方程的校验节点,自适应归一化最小和(adaptive-normalized min-sum, AN-MS)算法通过另外一个小于1的因子压缩了错误信息,提高NMS算法译码性能[10]。标度修正最小和(modified scaled min-sum, MS-MS)算法将NMS和偏移化最小和(offset min-sum, OMS)算法结合在一起,在校验节点更新处添加双重约束[11]。Genie-aided 自适应归一化最小和(adaptive normalized min-sum, ANMS)算法根据α和失败校验节点所占比例之间的关系建立查找表,进而根据查找表选择近优值,提升了非规则LDPC码的译码性能[12]。
NMS和密度演化最小和 (density evolution min-sum,DE-MS)算法使用单一的衰减因子,ANMS算法仅在特定条件下利用到两个衰减因子,一定程度上降低了译码性能且与MS-MS算法一样没有考虑校验节点度数分布问题,Genie-aided ANMS算法在搜索查找表时需要失败的校验节点个数,降低了译码速度。因此本文对现有算法进行分析和简化,提出一种新的方式来得到归一化因子,所提方法将校验节点分开考虑,每个节点利用各自的最小信息绝对值、平均信息绝对值和权值来近似获得各自的α。从仿真结果可以得出,本文提出的多归一化因子最小和(multiple normalized dactors min-sum, MNF-MS)算法在译码性能上优于所对比的算法。
1 LDPC译码算法简述
符号定义:
N(m) :集合N(m)={n:Hmn=1}剔除元素n后的子集合,Hmn为校验矩阵第m行、第n列所在位置的值;
M(n)m:集合M(n)={m:Hmn=1}剔除元素m后的子集合;
Cmn:校验节点m传至变量节点n的信息值;
Vnm:变量节点n传至校验节点m的信息值。
1.1 译码迭代步骤
LDPC主流译码过程是在校验节点和变量节点之间迭代传递信息值,利用BP传播理论修正错误比特,降低误码率,译码分为4个步骤:
1)设置初始迭代信息;
2)利用Vnm更新Cmn;
3)利用Cmn更新Vnm;
4)译出码字并判断是否达到停止迭代条件。
1.2 MS、NMS和AN-MS算法
MS、NMS和AN-MS算法主要在校验节点更新处对BP算法进行改进,信息值计算公式分别为
(1)
(2)
(3)
2 MNF-MS算法
2.1 已有算法α值计算
在对数似然比置信传播(log-likelihood ratio belief propagation, LLR BP)译码算法中,设Cmn的值为C1;MS算法中,设Cmn的值为C2;α能够通过E(|C1|)/E(|C2|)近似得到。E(|C1|)和E(|C2|)计算表达式为
(4)
(5)
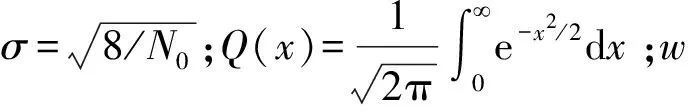
文献[9]提出使用概率质量函数来求不同迭代次数下的归一化因子αk,k代表迭代次数,表示为(6)—(7)式,但这种方式过于复杂,难以在迭代中实现。
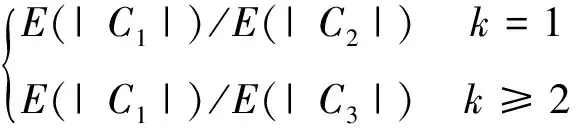
(6)
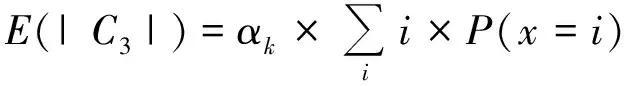
(7)
除上述使用概率论方法外,还可以通过蒙特卡罗仿真来求E(|C1|)和E(|C2|)[13],如(8)—(9)式,E(x)表示对x求期望。通过仿真不同迭代次数下的归一化因子可知,MS算法复杂度比DE-MS算法更高。
(8)
E(|C2|)=E(min(|X1|,|X2|…,|Xw|))
(9)
(8)—(9)式中,{Xl:l=1,2…,w}={Vmn′,n′∈N(m) }。
2.2 所提算法α值计算
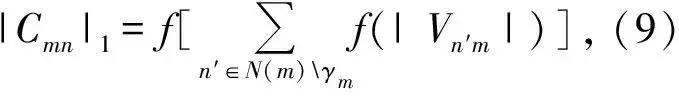
(10)
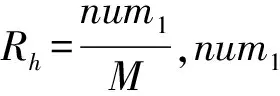
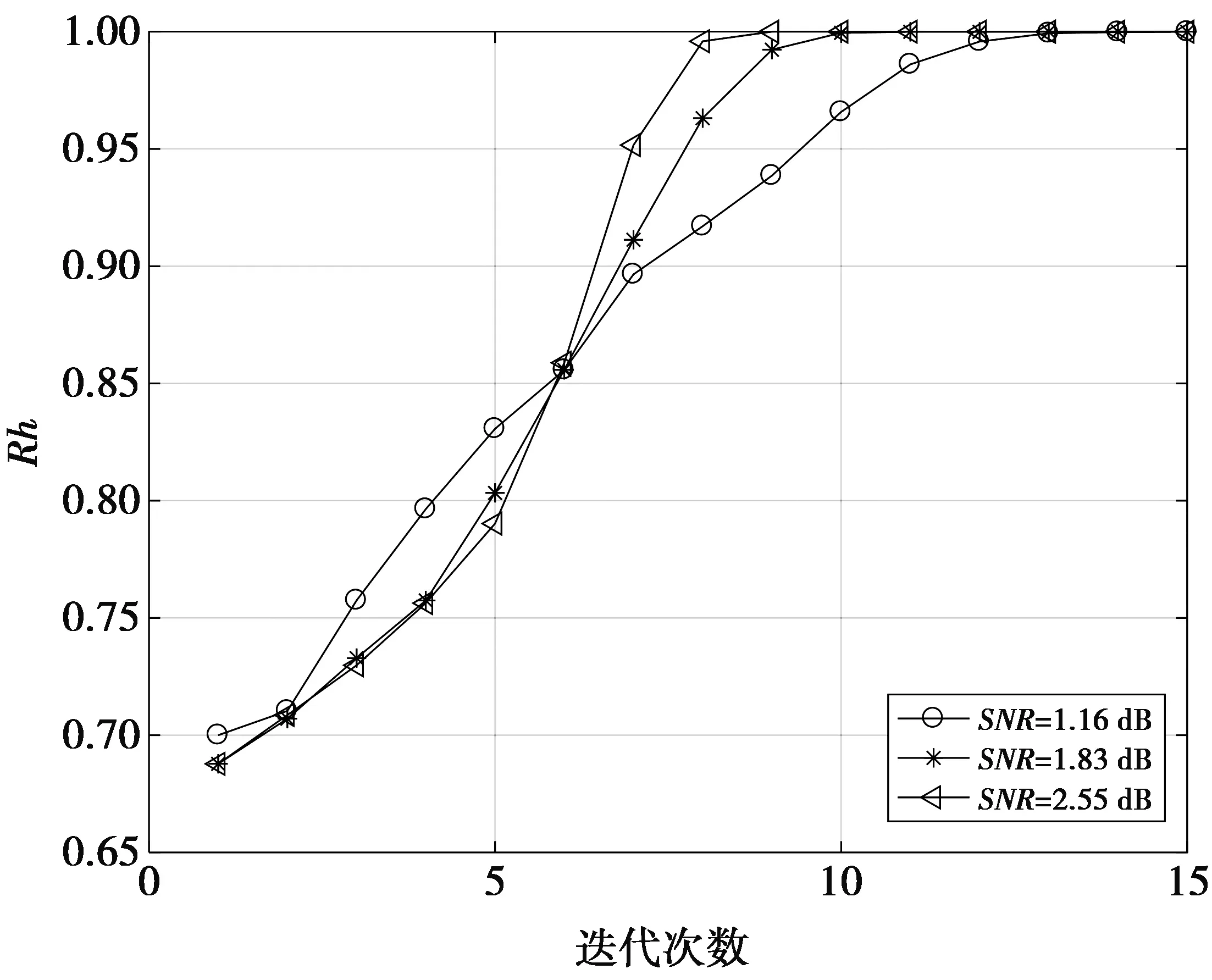
图1 正数权值所占比例Fig.1 Proportion of positive weight
文献[14]在不同迭代次数下使用不同的权值优化了smMS(single-minimum min-sum)算法,可以进一步改进(10)式为(11)式,校验节点信息更新公式变为(12)式。
(11)
(12)

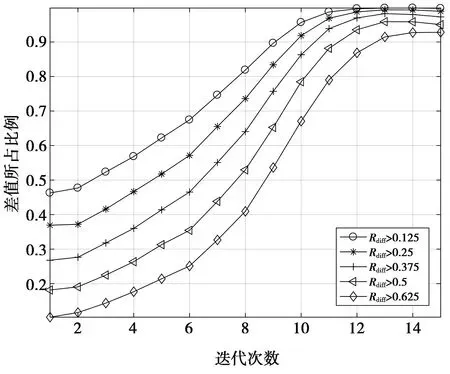
图2 不同差值所占比例Fig.2 Proportion of different differences
3 仿真结果与分析
本文仿真所使用的LDPC码字根据5G协议[15]的基准构造,码字类型有3种:(19968,3840)、(2496,480)、(16128,3840),前两种码字的码率(编码前有效信息比特数量与编码后信息比特数量的比值)为1/5,第3种码率为1/4;调制方式是BPSK,即1→1,0→-1;加扰噪声为加性高斯白噪声,信息序列由Matlab随机生成。对于信息比特长度K是3 840的码字,仿真帧数是3 000;对于信息比特长度是480的码字,仿真帧数为24 000,以保证在不同提升值情况下总信息序列长度是一致的。算法最大译码迭代次数为15。

表1 不同迭代次数下的权值Tab.1 Weights for different iterations
图3和图4展示了两种码率下各个算法的译码性能,可以看出本文所提MNF-MS算法比其余算法拥有更好的译码性能。图3中LDPC码字的码率为1/5,在误码率为10-6量级、信息序列长度为3 840时,MNF-MS算法的译码性能比DE-MS大约提高了0.15 dB,比AN-MS算法大约提升0.29 dB;当信息序列长度为480时,MNF-MS算法译码性能比DE-MS大约提高0.08 dB。图4中LDPC码率为1/4,在误码率为10-6量级时,MNF-MS算法译码性能比DE-MS算法提高了0.09 dB左右,比AN-MS大约提高了0.16 dB。

图3 码率为1/5,误码率比较Fig.3 Error rate comparison for 1/5 rate

图4 码率为1/4,误码率比较Fig.4 Error rate comparison for 1/4 rate
4 复杂度分析
表2列出了4种算法一次迭代所需的总运算复杂度,其中NMS和DE-MS算法复杂度不包含α值计算部分,ρi表示第i行的度数,δj表示第j列的度数,η的大小取决于上次迭代过程中不满足校验方程的节点个数,N为校验矩阵的总列数。从表2可以看出,所提MNF-MS算法在4种算法中复杂度是最高的,这是由于将归一化因子的计算加到了译码迭代过程中。NMS和DE-MS算法在求归一化因子的过程中,涉及对Q(x)的n次方求积分,对tanh函数的值求期望,这些计算在硬件中很难实现,通常做法是利用仿真找出最优值并保存在硬件中,但固定的因子会带来性能上的损失。AN-MS算法每次迭代后都需要解出码字并完成校验方程的检测,而在实际实现的时候为了提高译码速度,通常会选择在间隔几次迭代后再验证或者在达到最大迭代次数后直接输出结果,这时AN-MS算法将无法实现。本文算法所增加复杂度包括除法运算,但除法运算所需的比特位数较小,对于串行或者分层式[16]这些一次更新一个或者部分校验节点的译码结构,所提算法通过增加适量复杂度提高性能。分层式译码结构因其更快的收敛速度,在可编程逻辑门阵列LDPC译码器中得到广泛应用[17]。
5 结 论
本文提出一种使用多个归一化因子来完成迭代译码的算法。该算法将校验节点化整为零,对每个校验单独分析,利用其信息平均绝对值和最小绝对值的比值以及一个大于零的权值求得各自α,成功将α更新融入迭代过程中。仿真结果表明,所提MNF-MS算法与其他3种算法相比,译码性能更为优异。由于迭代过程增加了α的计算,复杂度有所提升,所提算法更适合分层式或者串行译码结构。
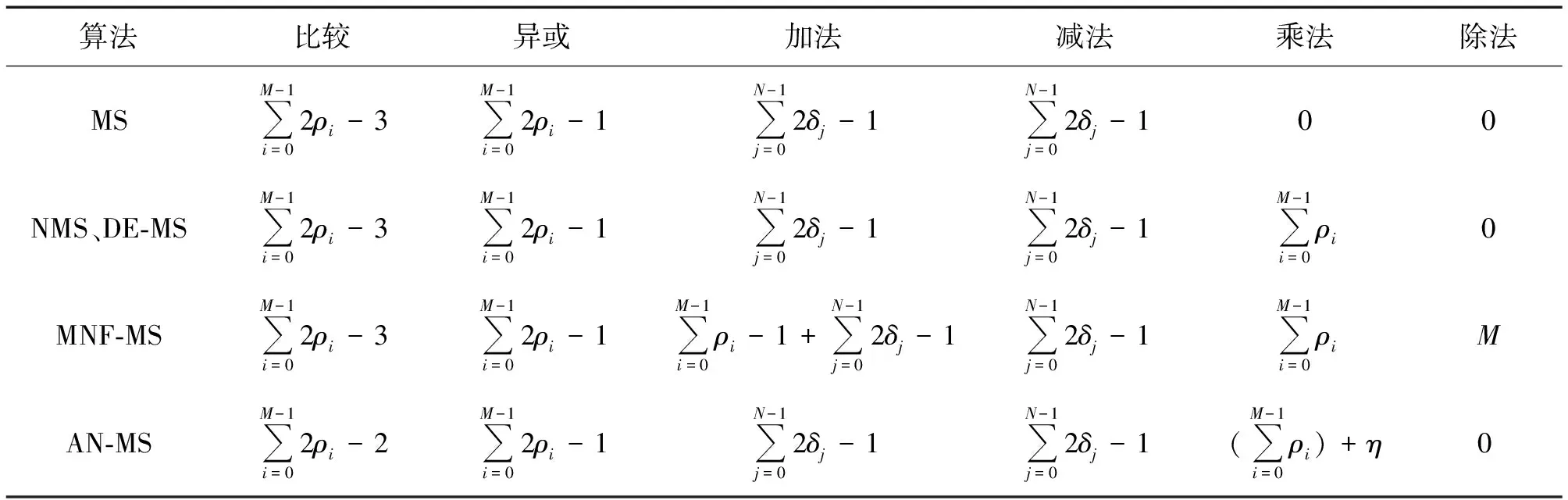
表2 不同算法复杂度Tab.2 Complexity of different algorithms

