文本分类中基于CHI和PCA混合特征的降维方法
唐加山,段丹丹
(南京邮电大学 理学院,南京 210023)
0 引 言
随着互联网技术的快速发展以及信息传播手段的不断进步,网络新闻与评论、电子邮件等电子文本数据逐渐增加,为了更有效地管理这些海量的文本数据,文本自动分类技术发挥着重要的作用。文本自动分类技术是指利用给定的分类体系,对未知类别的文本数据根据其特征自动判定其类别归属的过程[1]。
在文本分类过程中,由于文本数据的半结构化甚至非结构化的特点,通常需要使用向量空间模型(vector space model, VSM)[2]将文本表示成由一定数量特征词构成的空间向量,向量的维数即是文本集合中所有特征词的数量,这个维度通常可达几万维,甚至更高,所以文本特征空间的高维性是导致本问题的研究难点之一[3]。需要注意的是,并不是高维数据的每个维度都对文本的分类有实质性贡献,实际上,不同的特征之间可能存在不相关或者是冗余的现象,这不仅增加了许多噪声数据,造成了时间和空间开销的浪费,而且容易出现过拟合问题[4],显然,文本的特征降维是解决此类问题的有效方法之一。
1 相关工作
文本特征降维包括特征选择和特征抽取2个方法。特征选择方法是在不改变原始特征空间的条件下,从原始特征空间中按照某种评估函数选择一部分重要特征,组成一个新的低维空间用于后期的文本分类。常用的特征选择方法有[4]:文档频率(document frequency,DF)、互信息(mutual information,MI)、信息增益(information gain,IG)以及卡方统计(Chi-square statistics,CHI)等。在众多特征选择方法中,Yang等[5]指出IG方法和CHI方法的效果最好,且CHI方法具备更低的时间复杂度,因此,在实际应用中CHI是最好的特征选择方法之一,但CHI方法有其自身的缺陷,它在计算过程中,只统计了特征词是否在文本中出现,并未考虑其词频以及特征词的分布等信息。文献[6]使用样本方差来计算特征词的分布信息,并用最大词频信息来改进经典的CHI方法,在3个语料库上均取得了较好的结果。文献[7]通过在CHI方法中引入频度、集中度、分散度、位置信息这4个特征因子,并基于改进的词频-逆文本频率指数(term frequency-inverse document frequency,TF-IDF)权重计算公式,提出了降维后更能精确反映特征项权重分布的PCHI-PTFIDF(promoted CHI-promoted TF-IDF)算法。
特征抽取是通过将原始的特征空间进行某种数学变换,重新生成一个低维且各维度之间更独立的特征空间[4]。常用的特征抽取方法包括主成分分析(principal component analysis,PCA)、潜在语义索引(latent semantic indexing,LSI)、线性判别分析(linear discriminative analysis,LDA)等。其中,PCA适用于各种各样的数据,被视为用于特征抽取的有效技术[8]。文献[8]先使用信息增益筛选出初始特征词,再使用PCA进行二次降维,提出了一种基于PCA的特征混合选择方法,实验结果表明,该方法在英文数据集上可有效提高分类性能。文献[9]使用PCA方法对原始文本特征空间进行降维,再通过多重特征提取算法,在降维后的特征空间中过滤掉代表性较弱的特征项,随后使用支持向量机(support vector machines,SVM)分类器对文本进行分类,实验结果表明,该方法可有效提高文本分类的正确率。
针对特征选择CHI方法固有的缺陷,学者们提出了一些改进的方法,但据笔者所知,那些方法没有考虑特征选择后特征词之间是否仍存在某种相关性的问题,比如近义词等。PCA方法可以充分考虑特征项之间相关性,在特征降维的同时仍保留了原始特征空间最多的特征信息。基于此,本文利用PCA方法对CHI方法特征选择后的特征空间进行二次降维,提出一种基于CHI和PCA的混合特征降维方法(CHI-PCA),该方法可以进一步精简CHI方法特征选择后的特征空间,在降低特征维度的同时,还有利于提高分类性能,实验结果表明了所提方法的有效性。
2 基于CHI-PCA混合特征降维方法
本文提出的基于CHI-PCA的混合特征降维方法,主要由数据预处理、CHI方法特征选择以及PCA方法特征抽取3部分构成。数据预处理的目的是将输入的中文文本整理成CHI方法所需的输入形式,并降低其他文本符号对特征选择效果的影响,随后,将预处理后的文本经过CHI方法初筛出特征词,形成特征初选子集,再采用VSM模型进行文本表示,并使用TF-IDF方法[10]作为特征加权方式,形成初始特征向量,最后再将该向量输入PCA方法中进行二次特征抽取,得到最终特征向量。该特征向量即可输入分类器中进行训练,达到文本分类的目的。
2.1 数据预处理
本文的数据预处理主要包括文本清洗、类别匹配和文本分词3部分:①文本清洗包括去除特殊符号、去除多余空白以及去除停用词等,这样可以在一定程度上降低其他符号对后续分析的影响[11];②类别匹配是指将原始文本与其对应的类别一一匹配,因为本文使用的文本分类算法是有监督的,所以需要知道每一个样本所属的类别;③文本分词是指将一段文本切分成字、词或者短语的过程。
中文文本大都是以连续的字符串形式出现,切分粒度可以为字、词或者短语,根据文献调研,研究者们普遍认为选择词作为特征词要优于字或者短语[12],因此,本文选择词作为文本分词的粒度。假设经过文本清洗和类别匹配后的样本集为D={(d1,y1),…,(di,yi),…,(dn,yn)},其中,n为样本集数量,di表示第i个样本,yi为di对应的类别,且有yi∈Y={y1,…,yc},c为类别数量。对每个di进行文本分词后有di={wi1,…,wimi},其中,mi为第i个样本分词后特征词个数。现将特征词集{wi1,…,wimi},i=1,2,…,n去重后合并形成初始特征词集W={w1,…,wm},其中,m为去重合并后特征词的个数,该特征词集作为下一步CHI方法的输入。
2.2 特征初选子集
CHI方法的基本思想是通过计算实际值与理论值的偏差来确定理论的正确与否[13]。当CHI方法应用在文本特征选择时,主要衡量特征词与类别之间的相关性。假设有特征词wi,类别yj,其中,wi∈W,yj∈Y为训练样本所属的类别集。现假设特征词wi与类别yj相互独立,若原假设成立,则说明特征词对该类别完全没有表征作用;若原假设不成立,则认为特征词与类别之间具有相关性,即wi可以作为候选特征词。特征词与类别的关系表见表1,其中,n为样本集数量,已知wi与yj具有如表1的关系。
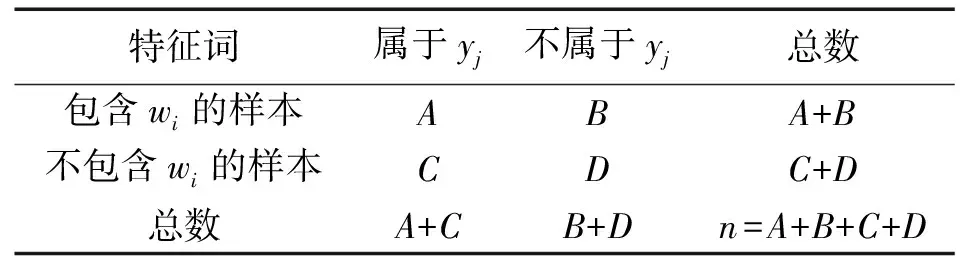
表1 特征词与类别的关系表Tab.1 Relationship between feature words and categories
特征词wi与类别yj的CHI值为[14]
(1)
当CHI值越大时,说明计算出的偏差越大,则原假设越不成立,即特征词wi与类别yj越相关。当c>2时,即处理多类别问题时,特征词wi对于整个样本集的CHI值通常取它与各个类别的CHI值的最大值,表示为[15]
(2)
按照上述方法,依次计算初始特征词集W中每个特征词对应的CHI值,依次由大到小排列,取前k个特征词作为特征初选子集WCHI={w1,…,wk},关于k的设定,由文献[16]所述,对于高维的特征词空间一般选择2%~5%的原始特征词集作为后续分析,即k的大小一般为0.02m~0.05m,其中,m为W的词个数。
根据VSM模型将训练样本D表示成由WCHI构成的特征向量矩阵,VSM的基本思想是将样本di映射为特征空间中的一个特征向量V(di)={(w1,qi1),…,(wk,qik)},其中,wk∈WCHI,di∈D,qik是第k个特征词wk在第i个样本中的权重[17]。本文使用的权重计算方法是TF-IDF方法,计算公式为[18]
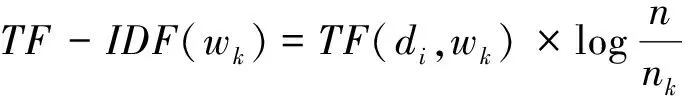
(3)
(3)式中:TF(di,wk)表示特征词wk在样本di中的词频;n表示样本数量;nk表示样本中包含特征词wk的样本数量;wk∈WCHI;di∈D。
本文采用(3)式将qik计算出后,可得到经过CHI方法特征选择后的文本表示矩阵为
ACHI=[q1,q2,…,qk]
(4)
(4)式中,任意qi=(q1i,q2i,…,qni)T,i=1,2,…,k。
2.3 特征再选子集
PCA方法的基本思想是将原来具有一定相关性的指标进行重新线性组合,形成一组新的彼此之间互不相关的指标进行后续的分析[19]。假设特征词wk是样本di的一个指标,则第2.2节中介绍的矩阵ACHI可看作是由n个样本和k个指标构成的一个n×k的观测样本数据矩阵。可知,这k个指标的协方差矩阵为
Sk×k=E((ACHI-E(ACHI))(ACHI-E(ACHI))T)
(5)
PCA方法旨在将原来的k个指标进行综合,形成k个互不相关的新指标,考虑以下线性组合
Zi=ACHIai=a1iq1+…+akiqk,i=1,2,…,k
(6)
(6)式中,ai=(a1i,a2i,…,aki)T,i=1,2,…,k。
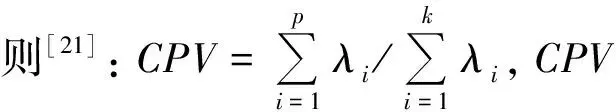
本文使用PCA方法的目的旨在将经过CHI方法特征初选后的k维特征进行二次降维,得到一组新的彼此之间互不相关的特征来进行后续的分类任务分析。根据线性组合(6)式得,经PCA方法特征再选后的数据矩阵为
Apca=ACHI×[a1,…,ap]=
(7)
降维后,矩阵Apca为n×p阶矩阵。
2.4 CHI-PCA方法流程
综上,本文提出的基于CHI-PCA的混合特征降维方法,具体流程可描述如下。
输出:经过CHI-PCA混合特征降维后的文本特征矩阵。
步骤1使用第2.1节中方法对样本集D′进行文本清洗,得到文本清洗后的样本集D={(d1,y1),…,(di,yi),…(dn,yn)},其中,di为预处理后的中文文本,yi∈Y为预处理后每个样本所属的类别,n为清洗后样本集的数量。对每个样本进行分词后得到第2.1节中的初始特征词集W,特征词个数为m;
步骤2使用第2.2节中CHI方法依次计算W中每个特征词对应的CHI值,由大到小排列,取前k(0.02m≤k≤0.05m)个特征词作为特征初选子集WCHI={w1,w2,…,wk},之后根据VSM并采用TF-IDF权重将训练样本表示成由WCHI构成的特征向量矩阵ACHI;
步骤3使用第2.3节中PCA方法针对步骤2中得到的矩阵ACHI进行特征再选,取CPV≥85%时的整数p作为主成分个数,得到混合特征降维后的矩阵Apca为n×p阶矩阵,p 本文实验数据使用的是搜狗实验室提供的搜狐新闻数据[22],本文选取了具有代表性的6个类别:IT、体育、娱乐、教育、汽车和财经,每一类别随机选取1 000条文本,共6 000条,再将总文本按照3∶1的比例进行训练集和测试集的划分,即训练集4 500条、测试集1 500条。 本文研究的问题属于文本分类问题,分类问题常用的评价指标有精确率P、召回率R和F1值,计算过程中需要用到混淆矩阵,见表2。 表2 混淆矩阵Tab.2 Confusion matrix 但是以上定义都是针对某一个类别yi,为了全局评价多类别的分类效果,本文使用宏平均(macro-averaging)来综合所有类别的F1值[15]。宏平均指的是每一个类别的F1值的算术平均值[18],假设|c|为样本所属的类别总数,计算公式为 (8) 为了和本文提出的基于CHI-PCA混合特征降维方法作对比,本文选择了传统特征降维方法DF,IG,CHI以及PCA方法进行实验,为了证明结果可靠性,实验先后选择了3种分类器,分别是Softmax回归(softmax regression)[24]、SVM分类[25]和K近邻(K-nearest neighbor, KNN)分类。根据第2.3节中介绍的方法流程,实验过程如下。 步骤1针对4 500条训练样本进行数据清洗,并进行中文文本分词,分词工具使用的是jieba分词,实验共提取了96 221个初始特征词; 步骤2利用CHI方法依次计算每个特征词对应的CHI值,关于特征词个数k的选择, 根据第2.2节中介绍以及步骤1知,最佳选择为1 924≤k≤4 811,根据此范围,本文共设计了不同特征维度的实验,分别取k=2 000,2 400,3 000,3 600,4 200,4 800,根据不同维度的特征词分别将训练样本表示成TF-IDF特征矩阵; 步骤3利用PCA方法分别针对步骤2中的特征矩阵进行二次降维,选择CPV≥85%时的整数p值作为主成分的个数,分别是p=1 177,1 355,1 586,1 794,1 976,2 133,根据第2.3节中介绍的特征变换公式,得到不同特征维度下降维后的新数据矩阵。 针对CHI-PCA方法,需依次完成上述3个步骤,再分别使用Softmax回归、SVM分类和KNN分类进行训练,这3种分类器的实现均是基于python 3中sklearn模块实现的。SVM分类器采用的是线性核函数[26],惩罚因子C使用的是网格搜索方法[27]来确定的,本文展示的实验结果均是实验中最优参数C下的分类结果。KNN分类算法中k值采用的是交叉验证方法选择的。对比实验中,分类器的参数选择和上文保持一致。为了从全局评价多类别的分类效果,图1—图3的评价指标使用的是F1的宏平均值,展示了在不同特征维度下DF,IG,CHI以及CHI-PCA方法结合3种分类器的实验结果。 图1 使用Softmax回归的实验结果对比Fig.1 Comparison of experimental results using Softmax regression 图2 使用SVM分类的实验结果对比Fig.2 Comparison of experimental results using SVM classification 可知,在不同特征维度下,CHI-PCA方法的实验效果整体上优于其他3种方法。图1中,当使用Softmax回归分类器时,CHI-PCA方法的F1宏平均值相比DF,IG和CHI方法分别平均高出1.3%,0.4%和0.1%;图2中,当使用SVM分类器时,CHI-PCA方法的F1宏平均值相比DF,IG和CHI方法分别平均高出1.5%,0.5%和0.3%;图3中,当使用KNN分类器时,CHI-PCA方法的F1宏平均值相比DF,IG和CHI方法分别平均高出2.7%,1.3%和0.7%。因此,CHI-PCA方法提取的特征对于本文实验中所使用的3种分类器的分类性能均有所提升。 图3 使用KNN分类的实验结果对比Fig.3 Comparison of experimental results using KNN classification 在特征维度为2 000时,CHI-PCA方法的F1宏平均值相比DF方法提升最多,特别是在图3中使用KNN分类器时,前者为0.898,后者为0.865,提升了3.3%,图2中提升了2%,图1中提升了1.4%,说明在特征维度较低时,CHI-PCA方法选择出的特征比DF方法选择出的特征质量更高。 在特征维度为4 200时,CHI-PCA方法的整体分类效果达到最优,比如图1—图3中的F1宏平均值分别为0.931,0.933和0.911,但当维度继续增加达到4 800时,分类效果略微下降或者持平,F1宏平均值分别为0.93,0.933和0.907,说明此时特征之间存在冗余,维度的增加不能对分类效果有很好的提升。 为了更进一步验证本文所提方法在每个类别上的分类效果,下面选择在最佳特征维度4 200时,分别展示CHI-PCA方法以及DF,IG和CHI方法在各个类别上的F1值。此外,还加入了PCA方法进行对比,按照CPV≥85%准则,降维后特征维度是3 646,随后将矩阵分别输入3种分类器,参数选择方法和上文保持一致。结果见表3—表5。 表3 使用Softmax回归的各个类别的效果对比Tab.3 Comparison of the effects of various categories using Softmax regression 表4 使用SVM分类的各个类别的效果对比Tab.4 Comparison of the effects of various categories classified by SVM 表5 使用KNN分类的各个类别的效果对比Tab.5 Comparison of the effects of various categories using KNN classification 从表3—表5可知,5种方法均在体育类别上F1值达到最高,而在IT和财经类别上的分类性能欠佳,原因是语料库中体育类别含有的特征词更具有类别区分度,使得分类效果更好。 由表3知,在使用Softmax回归分类器时,CHI-PCA方法在IT、教育和财经类别上的F1值均高于其他4种方法,最高提升了3.1%;表4中,CHI-PCA方法在所有类别上的F1值都高于DF方法,最高提升了3.2%;表5中,CHI-PCA方法在IT、体育、娱乐、汽车和财经5个类别上的F1值均高于其他4种方法在相应类别上的F1值,最高高出4.9%。这说明了CHI-PCA方法在各个类别上的分类性能也是可观的。 此外,由表3—表5可得,PCA方法在3种分类器下的F1宏平均值,即所有类别F1值的平均值分别为0.919,0.931和0.905,而CHI-PCA方法的F1宏平均值分别为0.931,0.933和0.911,可以看出,相比于PCA方法,CHI-PCA方法在整体上也表现出了更好的分类性能。 本文在解决中文文本分类特征降维的问题中,考虑CHI方法特征选择后的特征仍有可能存在相关性,因此,使用PCA方法对CHI方法特征选择后的特征空间进行二次降维,提出了一种基于CHI-PCA的混合特征降维方法。实验结果表明,在不同特征维度下,CHI-PCA方法实验效果整体上优于DF,IG,CHI和PCA方法,在各个类别上的分类性能也是可观的。本文所提方法说明了两阶段的CHI-PCA特征降维方法是可行的,不仅满足了特征降维的需求,还提高了分类性能。本文所提方法不足在于未考虑类别特征词的平衡性,当某些类别特征词个数较少时会导致该类别分类性能下降,这将是下一步的研究方向。另外,分类方法与语言的不同是否有关联性,以及与文献[8]的比较,也将作为下一步的研究方向和内容。3 实验分析
3.1 实验数据
3.2 评价指标

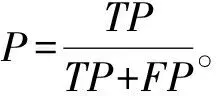

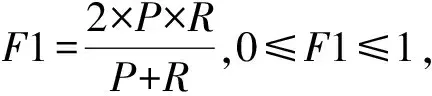
3.3 实验过程与结果分析
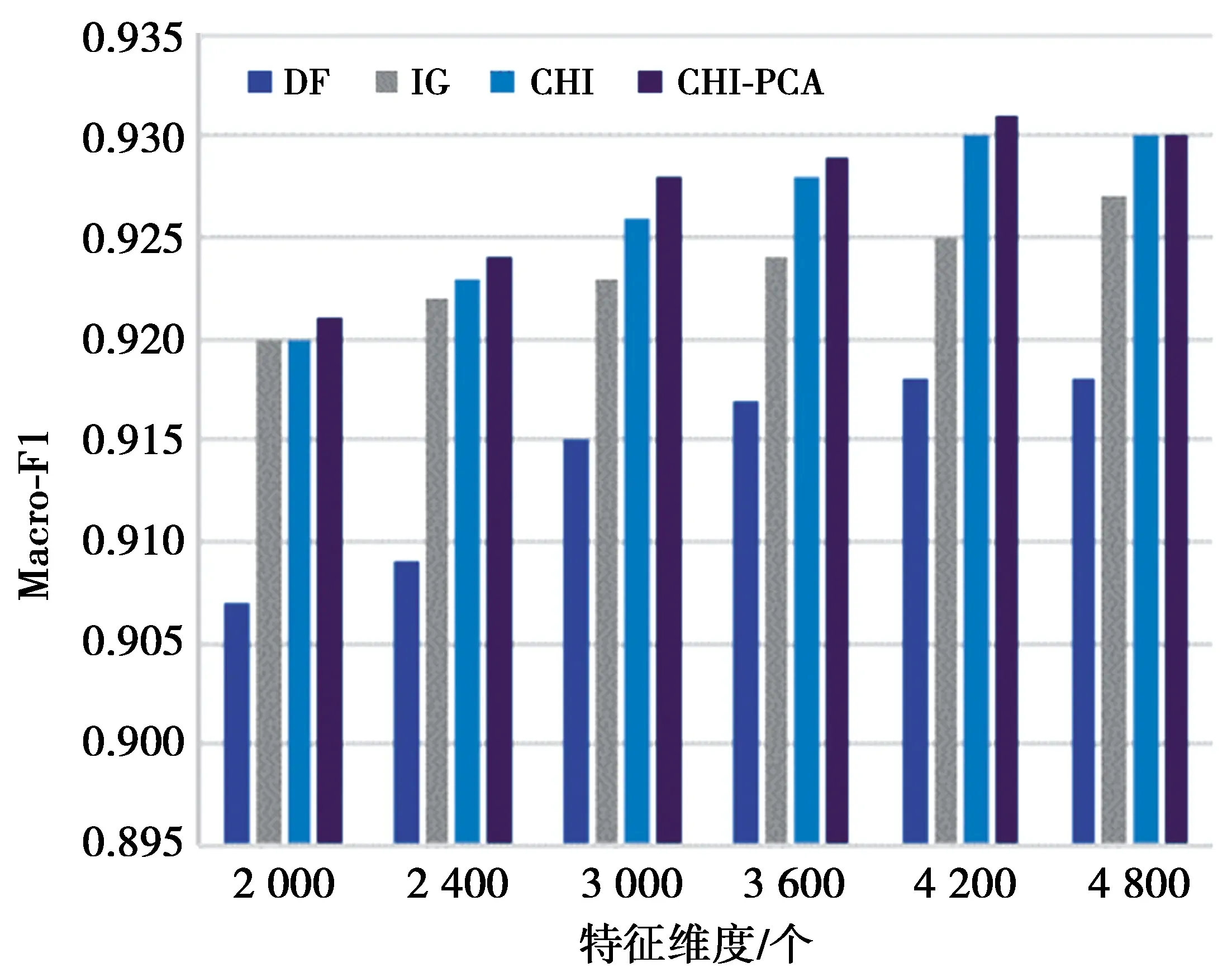
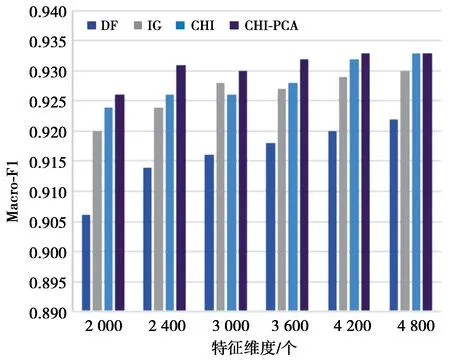
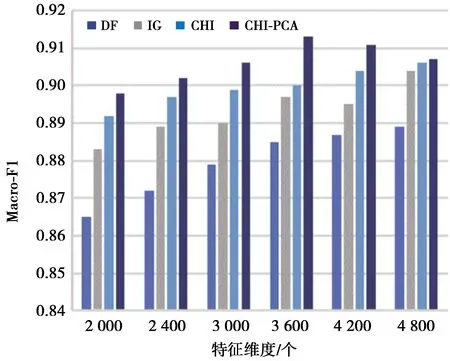

4 结束语

