约束优化的空间变迹算法的旁瓣抑制应用

徐 正, 巩光众,2, 罗运华,*, 李广德

(1. 中国科学院空天信息创新研究院, 北京 100094; 2. 中国科学院大学电子电气与通信工程学院,北京 100049; 3. 中国人民解放军96901部队, 北京 100094)

0 引 言

合成孔径雷达作为一种主动探测雷达,具有全天时全天候的特点,已广泛应用于国土测量、环境监测、灾害预警和军事侦察等领域[1]。合成孔径雷达回波信号具有很大的动态范围,最高可达50 dB以上[2],而线性调频信号经脉冲压缩后为sinc函数的形式[3],峰值旁瓣比仅为-13.26 dB,导致强目标的旁瓣会覆盖临近弱目标的主瓣,造成图像细节的损失和漏检[4-5]。传统抑制合成孔径雷达旁瓣的方法是频域加窗[6],然而该方法在抑制旁瓣的同时也造成了主瓣的展宽,从而导致图像分辨率降低[6]。压缩感知[7-8]和图像域去卷积[9-15]等方法可以在保持图像分辨率的同时有效抑制目标的旁瓣,但其仅适用于目标区域稀疏的场景,如海洋遥感等,而对于复杂的目标场景和低信噪比的回波信号处理效果并不理想;空间变迹(spatially variant apodization, SVA)算法则可以有效抑制复杂场景目标的旁瓣。

SVA是一种非线性的频域加窗方法,1995年,Stankwitz等[16]首先将其应用到合成孔径雷达旁瓣抑制中。空间变迹滤波的思想是对于不同的采样点,根据其相邻的数据自适应地选择合适的滤波参数对回波信号执行非线性的滤波操作,映射到空间域则为3点卷积[17]。通过该方法,可在不损失图像分辨率的前提下抑制目标的旁瓣。然而,该方法仅适用于接收系统的采样率为Nyquist采样率的整数倍的场景,对非Nyquist采样率采样的数据则不适用[18]。通用SVA(general SVA, GSVA)[19-20]修改了频域加窗函数,可以实现对非整数倍Nyquist采样率数据的旁瓣抑制,但是其仍保留了部分旁瓣[21];鲁棒SVA(robust SVA, RSVA)算法[22-23]通过扩展FIR滤波器的维数,将传统SVA的三点卷积扩展为五点卷积,增加了滤波器的灵活度,可以有效地抑制旁瓣,但仍然受到相位偏差的影响导致主瓣能量的降低[24];改进的SVA(modified SVA, MSVA)对RSVA进一步改进,通过选取有效点的方式进一步抑制了旁瓣,同时一定程度地提高了主瓣能量[25-26],然而其约束条件仍不够严谨,不能保证频域滤波窗的单调性,导致其对于复杂的目标场景回波,旁瓣抑制效果不佳,主瓣能量的提高幅度并不明显。文献[27]中提出了将RSVA与卷积神经网络(convolution neural networks, CNN)相结合的方法,即采用RSVA算法处理信号的旁瓣,CNN算法处理信号的主瓣,该方法有效保持了主瓣的能量,但由于其以固定的阈值作为区分主瓣与旁瓣的标准,算法鲁棒性较低,不能应用于复杂的目标场景。本文在已有算法的基础上进一步优化了约束条件,保证了滤波窗的单调性,在有效抑制旁瓣的同时,相较于其他算法在不同分辨率条件下都实现了对图像主瓣能量的提升。

1 传统SVA算法

SVA是一种非线性的自适应频域加窗旁瓣抑制算法,可用于对整数倍Nyquist采样数据的旁瓣抑制。其频域窗型为

(1)

式中:f为频率；w为滤波器权重；f0为带宽；fs为采样率。频域的乘积在时域的表现形式为卷积,故滤波器在时域的形式为三点卷积[28],其表达式为

g′(n)=g(n)+ω(n)g(n-1)+ω(n)g(n+1)

(2)

g′(n)为滤波器处理后的结果,参数优化的目标为在0≤ω(n)≤1/2的前提下,使得|g′(n)|2最小[29],由于SVA处理的数据为复数据,当实部与虚部同时优化时,其最优解必然存在于由实部和虚部共同确定的固定模值的圆上。此时,求得的最优解并不能保证信号的实部与虚部都达到了最小值,故将复数据的实部与虚部分开处理,可使实部与虚部同时达到最小值,而信号的能量为其模值的平方即信号实部与虚部的平方和,故此时求得的解即为最优的旁瓣抑制结果[3],求得最优权值的计算方法为

(3)

令y为第n个点临近两个点的平均值,即y=[g(n-1)+g(n+1)]/2,当ω(n)<0时,g(n)与y符号相同,该点位于主瓣上,故保持其幅度不变;当0≤ω(n)≤1/2时,g(n)与y符号相反,且该点幅值的绝对值小于y。此时,该点位于旁瓣上,故将其抑制为0;当ω(n)>1/2时,g(n)与y符号相反,且该点幅值的绝对值大于y。此时,该点位于叠加有旁瓣的主瓣区域中,可将其赋值为该点的值与临近点平均幅值的和[16];故SVA处理的最终结果为

(4)

2 约束优化的旁瓣抑制算法

对于非整数倍Nyquist采样率采样的数据,由于存在相位偏差,传统SVA算法已经不适用于此场景,处理后会存在大量的剩余旁瓣。因此,可考虑增加滤波器的阶数来补偿相位偏差对于数据的影响。本文采用5点卷积的二阶FIR滤波器,滤波器的时域形式如下:

(5)

(6)

频域滤波窗对应的单位脉冲响应为

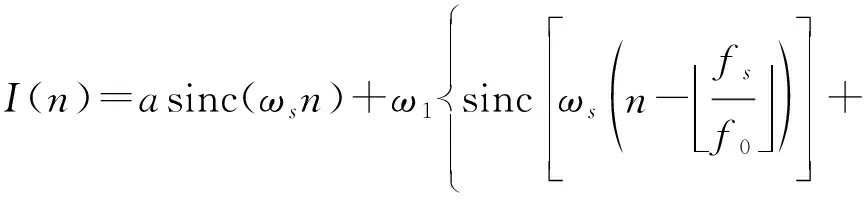
(7)

其中,ωs=f0/fs。优化的目标同样是最小化|g′(n)|2,然而若不加约束,其最优解必然为0,因此为避免无效的滤波窗,设置以下约束:

I(0)=1

(8)

(9)

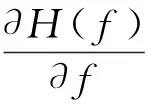
(10)

(11)

其中,式(8)为保证权系数在原点处经过一个单位增益的支流分量,式(9)和式(10)保证了频域滤波窗的单调性和非负性,将式(8)代入式(7),将式(9)和式(10)代入式(6)分别可得

(12)

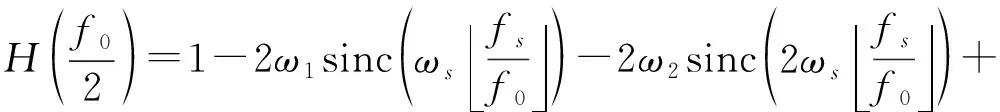
(13)

(14)

将式(12)代入式(5)可以得到滤波器的最终表达:

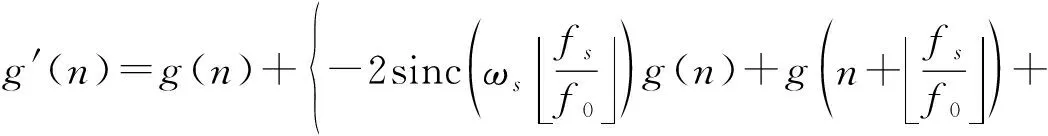
(15)

式(11)、式(13)和式(14)所表示的直线围出了一个封闭区域,图1展示了其中的两种情况。

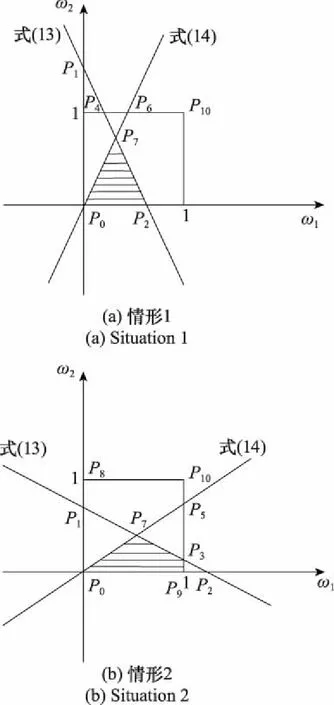
图1 约束不等式围成的区域Fig.1 A region bounded by constrained inequalities

根据约束优化的理论,最优的权值点必然存在于不等式围成的封闭区域的顶点,即为本文选取的有效点。如图1(a)中的P0、P2、P7和图1(b)中的P0、P3、P7、P9即为在不同情形下选取的有效点,将选取的有效点分别代入式(15),从而优化滤波器的结构。

本文提出的改进的旁瓣抑制算法的流程如下:

步骤 1根据输入回波信号的带宽和采样率等参数构建约束不等式(11)、式(13)和式(14);

步骤 2根据构建的约束不等式选取合适的有效点;

步骤 3将选取的有效点代入滤波器式(15),分别求出不同有效点权值数据下滤波器的旁瓣抑制结果;

步骤 4比较处理结果,若结果中的最大值与最小值异号,则最终的输出为0;若同号则选取结果中模值最小的点作为最终的输出结果。

步骤4中,处理结果异号,表示在这两个有效点的滤波权重之间必然存在另外一种权重的选择,使得滤波器的输出结果恰好为0,因此可判断该点必然为旁瓣,故此时将输出结果置零以抑制旁瓣[30]。

3 仿真验证

3.1 测试指标

合成孔径雷达旁瓣抑制效果的评价指标主要有以下3种:

(1) 峰值旁瓣比[31](peak side lobe ratio, PSLR):信号的最大旁瓣峰值与主瓣峰值的比值(dB),计算方法为

(16)

(2) 积分旁瓣比(integral side lobe ratio, ISLR)指的是所有旁瓣能量之和与主瓣能量的比值(dB),计算方法为

(17)

(3) 主瓣宽度指的是信号顶点两侧幅度相较于顶点下降3 dB内的所有点的宽度。

未经处理后的脉冲压缩后的线性调频信号,其PSLR为-13.26 dB,ISLR约为-10 dB,相较于合成孔径雷达目标回波信号的大动态范围,容易出现强目标掩盖弱目标的情形,造成漏检。

由于各SVA改进算法都可以有效的抑制目标的旁瓣,但是会造成主瓣能量的降低,因此本文将重点关注利用各算法处理后,剩余主瓣的能量大小。同时,本文将采用4点目标仿真的形式测试算法的性能,因此需要对以上指标的计算方法做一定的修改,其中主瓣宽度的计算方法修改为4个目标所有主瓣3 dB宽度的和;峰值旁瓣比的计算方法修改为处理后的信号最大旁瓣与最小主瓣幅值的比值;主瓣能量计算方法为归一化的表示,及计算各算法处理后各目标3 dB主瓣能量的和与原始回波3 dB主瓣总能量的比值。

3.2 一维点目标测试

对于单一一维点目标的回波,改进的SVA算法可以有效抑制其旁瓣,并且同时保持主瓣的能量。为验证本文提出算法的有效性,模仿复杂目标场景的回波信号,本文采用4点一维目标回波信号进行测试,通过调整目标间的斜距差,测试在不同场景下各旁瓣抑制算法的性能。在这种测试条件下,各改进SVA算法依然可以有效抑制旁瓣,然而主瓣的能量大小也将随着目标间距的减小而减小,当目标间距过小时,经SVA处理后的图像将会整体偏暗,丧失图像的细节信息。因此,对于各改进的SVA算法来说,相对于降低PSLR和ISLR,保留图像的主瓣能量更加重要。本文采用的测试线性调频信号的带宽为840 MHz,采样率为1 GHz,信号时宽为80 μs,场景中心斜距为100 km,在此雷达参数下根据式(18)计算的理论距离向分辨率为0.158 2 m。设置目标间距为0.35 m,原始回波经脉冲压缩后的波形、MSVA和本文提出的改进算法旁瓣抑制的处理后经升采样的结果对比如图2所示。

图2 不同算法旁瓣抑制效果对比Fig.2 Comparison of sidelobe suppression effect of different algorithms

(18)

式中：ρr为距离向分辨率;fr0为距离向采样率；c为光速。

其中,黑色实线表示的是未经旁瓣抑制处理的原始信号,使用本文所述计算方法计算,其PSLR为-14.732 6,蓝色实线表示的是经MSVA抑制旁瓣后的信号，红色实线表示的是经本文算法抑制旁瓣后的信号。从图2中可以看出,在高分辨率且目标区域复杂的场景,本文算法相较于MSVA具有更优的峰值旁瓣比,并且保留了更高的主瓣能量。

表1展示了在相同雷达参数条件下对于不同目标间距下利用MSVA与本文算法分别进行旁瓣抑制处理后信号归一化的主瓣能量。从表1中可以看出,目标间的距离越近,两种算法旁瓣抑制处理后保留的主瓣能量也越低。同时,本文改进的算法相较于其他改进的SVA算法旁瓣抑制效果也更好,主瓣能量提升幅度也更大,因此本文算法可应用于更加复杂的目标场景。

表1 不同算法抑制旁瓣后主瓣能量比较Table 1 Comparison of main lobe energy after sidelobe suppression by different algorithms

表2对比了目标间距为0.35 m时,原始回波信号以及不同算法抑制旁瓣后信号的PSLR和ISLR。可见,在目标间距较小时,采用本文提出的改进的旁瓣抑制算法相较于MSVA旁瓣抑制处理后的信号同时具有更优的PSLR和更优的ISLR,此时MSVA的旁瓣抑制效果已不够理想。

表2 不同算法抑制旁瓣后的性能比较Table 2 Performance comparison of different algorithms for sidelobe suppression

3.3 图像测试

将本文所提算法应用于实际遥感图像,线性调频信号的带宽为420 MHz,采样率为500 MHz,方位向带宽为203 Hz,脉冲重复频率为1 250 Hz,方位向过采样率为6.16,距离向过采样率为1.19,未处理前的原始图像如图3所示。图像中存在大量的强目标,如图中黄色方框内所示,且都存在强度较大的旁瓣,造成图像噪点较多,且相对模糊,强目标的旁瓣最大可跨越250个像素以上,在这个范围内的若目标极易被该强目标的旁瓣所覆盖,因此对图像进行旁瓣抑制尤为重要。

图3 原始遥感图像Fig.3 Original remote sensing image

分别经MSVA和本文旁瓣抑制处理后的图像如图4所示,计算图像的归一化总能量(处理后图像总能量与处理前图像总能量的比值)如表3所示,处理后图像的直方图如图5所示。可见经MSVA和本文算法处理后,目标的旁瓣都得到了有效的抑制。从表3可知,本文算法处理后的图像能量更高。由图5可知本文改进算法处理后的图像对比度更高,保留了更多的图像细节,旁瓣抑制效果要明显优于MSVA及其他改进SVA算法。

图4 MSVA和本文算法抑制旁瓣后的图像对比Fig.4 Image contrast between MSVA and the proposed algorithm after sidelobe suppression

表3 不同算法抑制旁瓣后图像归一化能量的比较Table 3 Comparison of normalized energy of image after sidelobe suppression by different algorithms

图5 两种算法处理后图像的直方图对比Fig.5 Histogram comparison of two algorithms after processing

3.4 信噪比对算法性能的影响

为进一步验证算法在复杂场景下的性能表现,对一维点目标回波信号加入了不同信噪比(signal to noise ratio, SNR)的高斯白噪声,测试在不同信噪比下,经本文改进算法处理后的PSLR。临近目标间的斜距为0.35 m,带宽为840 MHz,采样率为1 000 MHz,未添加噪声时,PSLR为-47.707 4 dB,结果如图6所示。

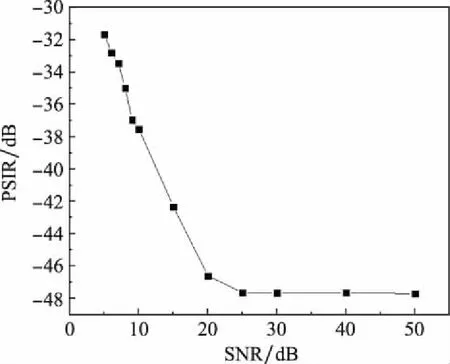
图6 信噪比对算法性能的影响Fig.6 Influence of SNR on algorithm performance

从图6中可见,在信噪比小于20 dB时,本文算法抑制旁瓣后信号的PSLR随信噪比的增大呈线性变化趋势,信噪比大于25 dB时,PSLR达到最优,此时其基本不随信噪比变化。即使在信噪比5 dB左右的复杂场景,本文算法处理后的信号,其PSLR仍小于-30 dB。可见,算法具有很高的鲁棒性。

4 结 论

本文在已有旁瓣抑制算法的基础上通过约束优化的方式做出了改进,改进的主要目标为在有效抑制旁瓣的同时尽可能的保留主瓣的能量。经测试,在复杂目标场景,本文提出的改进算法相较于已有的其他算法主瓣能量提升明显,且同时可以达到更低的PSLR和ISLR。同时，为验证本文算法在不同场景的有效性,采用添加噪声的方法测试对同信噪比回波数据旁瓣抑制操作的有效性,验证了本文算法的有效性。

SVA算法可以实现对目标旁瓣的有效抑制,但同时也改变了图像的统计特性,不利于对数据的后续处理[18]。当前旁瓣抑制处理多存在于成像阶段,可考虑将SVA扩展到成像后的图像后处理阶段,使其避免影响后续处理且方便扩展于光学成像等其他应用场景。