多载波OFDM信号识别方法

朱立为, 黄知涛

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

近些年来,由于无人机的大量使用,无人机非法入侵事件时有发生,催生了以无人机为目标的对抗技术研究。而在通信无源对抗领域中,针对无人机测控数传信号的盲处理技术研究也成为一个十分重要的课题,而无人机测控数传信号采用的便是正交频分复用(orthogonal frequency division multiplexing, OFDM)信号。OFDM信号的盲处理技术研究,包括信号的检测识别、参数估计、解调及测角定位等技术问题。由于OFDM信号采用频分多路复用(frequency division multiplexing,FDM)技术,适用于高数据速率的无线传输,其非合作处理技术也与单载波调制信号略有不同。因此,首先要解决OFDM信号的识别问题。

因为OFDM信号在时域上有类高斯特性,所以许多文献中提出用高阶矩或者高阶累积量来识别多载波与单载波信号。早期,文献[1]中用二阶矩与高阶矩及高阶矩之间的比值联合来识别,当信噪比(signal to noise ratio, SNR)大于5 dB时,识别率大于90%,识别依赖一确定阈值,只能用于其特定环境条件下。文献[2]中通过计算分析不同子载波调制的OFDM信号四阶累积量的值分布与一般单载波信号的分布情况,设定合适的经验门限来区分单载波调制信号与OFDM信号,该方法受频率影响大。文献[3]基于参数极大似然函数的识别方法,需要提前估计SNR。文献[4-5]中基于多尺度小波分解后的特征向量的支持向量机(support vector machine, SVM)分类方法,此方法无法避免小波分解层数的选择及运量大的问题。近来随着大数据深度学习研究的兴起,采用深度学习的方法来实现OFDM信号识别也屡见不鲜,如文献[6-7],但深度学习方法比较依赖训练数据的质量,且对信号环境的范化能力也有待提高。

实际上在无人机测控信号非合作处理环境中,不但要考虑区分OFDM信号与单载波信号,还要考虑OFDM信号与其他多载波信号之间的区分,如频分多址(frequency division multiple access, FDMA)信号、跳频(frequency hopping, FH)通信信号、多载波时分多址(multi frequency time division multiple access, MF-TDMA)信号等,存在信号处理环境极为复杂、信道选择性衰落、多普勒以及多径等问题。

本文提出了基于包络相关谱的OFDM识别算法,该方法既利用了OFDM信号的循环前缀的特征,又利用其类高斯性。通过计算OFDM信号包络相关谱，在变换域中实现OFDM信号的识别。该方法并不需要任何信号先验信息,同时还能估计出OFDM信号的子载波符号速率。

1 信号模型

1.1 单载波信号模型

在加性信道噪声条件下,单载波传输系统中,接收的数字基带信号的一般数学表达式为

()=()+()

(1)

(2)

式中:()为加性噪声;()为脉冲成型形状;为第个码元所对应的电平值,为码元持续时间。

1.2 OFDM多载波信号模型

(3)

得到基带时间连续的OFDM信号表达式如下:

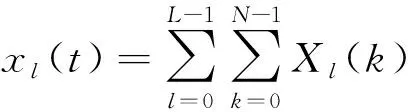
(4)

对式(4) OFDM基带信号进行采样,令=+,=,=,可以得到OFDM符号的离散时间表达式如下:

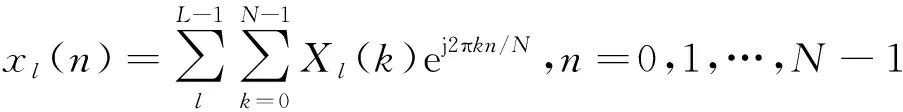
(5)

易得基带OFDM接收符号表达式为

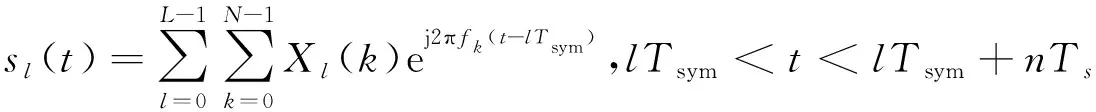
(6)

考虑信道的带限情况,则有()=,(-)，其中,(-)为信号脉冲形状。

因此,在加性高斯白噪声条件下的多载波OFDM信号接收模型表达式如下:

()=()+()

(7)

2 包络相关谱

2.1 单载波信号包络相关谱

由文献[9]可知,数字调制信号的包络傅里叶变换(本文中定义为包络谱)在符号速率处存在离散谱线,可以用来估计信号的码速率。

利用式(1)，假设信号为复信号,则信号的包络为|()|,有如下推导过程:

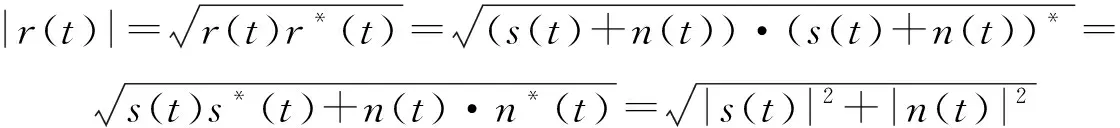
(8)

所以其包络平方|()|=|()|+|()|,由于复包络绝对值的傅里叶变换进行推导比较复杂,对复包络平方的傅里叶变换进行了理论推导,易知：

(9)

设()的傅里叶变换为(),根据傅里叶变换的基本性质中的频域卷积性质,可得()的傅里叶变换为(12π)()*()(*表示卷积),因此得到其完整包络谱为

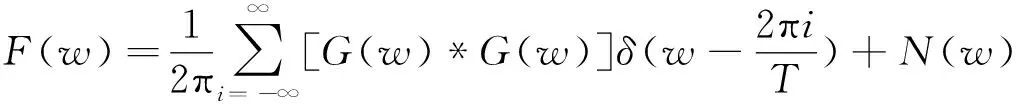
(10)

而在通信过程中,信号都是带宽受限的,即当||>2π时,有()=0,于是在频率=±2π处出现了离散谱线。

同理,可以推导包络相关谱过程:

()=E{|()‖(-)|}=E{|()+()‖(-)+(-)|}

(11)

式中：E(·)表示求均值。

其中，设接收信号的采样长度为,使得和取值满足以下条件:

(12)

由于()与()不相关,且加性高斯白噪声非相关性可知E{|()(-)|}≈0,可得单载波信号的包络谱相关波形:

()=E{|()(-)|+|()(-)|}=E{|()(-)|}

(13)

根据傅里叶变换的基本性质中的相关性质，可以得单载波信号完整的包络相关谱:

()=F[E{}]=F[E{|()(-)|}]=

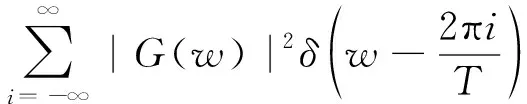
(14)

同理可得,在频率=±2π处会有离散的包络相关谱线。

综上可以看出,包络相关谱与包络谱相比,具有一定的噪声抑制能力。

2.2 多载波OFDM信号的包络相关谱

前面已经推导介绍了单载波信号的包络相关谱,很显然,包络相关谱具有抑制加性高斯白噪声的作用，可以作信号的符号速率。下面推导多载波OFDM信号的包络相关谱。

OFDM信号表达式如下:

(15)

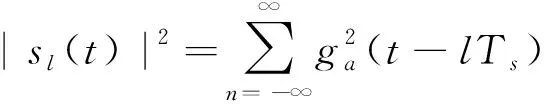
(16)

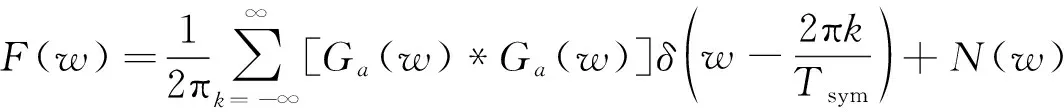
(17)

而在通信过程中,信号都是带宽受限的,对于OFDM信号，其带宽为,为子载波总数据,即当||>2π时,有()=0,于是在频率=±2π,≤处出现了离散谱线，且具有频域周期性。

同理,可以推导包络相关谱过程：

()=E{|()‖(-)|}=E{|()+()‖(-)+(-)|}

(18)

其中，设接收信号的采样长度为,使得和取值满足以下条件:

(19)

由()与()不相关,且加性高斯白噪声非相关性可知E{|()(-)|}≈0,可得单载波信号的包络谱相关波形:

()=E{|()(-)|+|()(-)|}=E{|()(-)|}

(20)

根据傅里叶变换的基本性质中的相关性质可以得多载波OFDM信号完整的包络相关谱：

()=F[E{}]=F[E{|()(-)|}]=

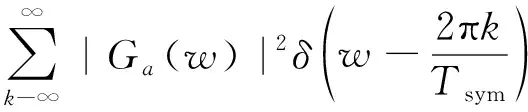
(21)

综上可以看出,在频率=±2π,≤处会有离散的包络相关谱线,且谱线具有等间隔周期性,后续可作为区分多载波OFDM信号与单载波信号的有效依据。同时,对多载波OFDM信号,包络相关谱的一些性能仍然存在,即与包络谱相比,具有一定的噪声抑制能力。

通过第2节对单载波信号和多载波OFDM的包络相关谱的推导可知:

(1) 通信信号带限条件下,单载波信号的复包络相关谱只在正负符号速率的频率位置出现离散的谱线;

(2) 多载波OFDM信号在带限条件下,由于其具有多子载波特性,其复包络相关谱的离散谱线会出现在正负子载波符号速率1至倍的频率位置,且具有周期性,其中为子载波数;

(3) 包络相关谱相比包络谱具有更好的高斯白噪声抑制能力。

因此,本文识别OFDM信号的策略是通过计算信号的包络相关谱,然后检测其离散谱线,判断其周期性来区分是OFDM信号还是单载波信号。

3 仿真分析

3.1 识别率

为了验证包络相关谱对OFDM信号的识别性能,本文仿真时采用正确识别率作为指标,来衡量OFDM信号的识别性能,定义识别正确率RMP=MC×100%。其中,表示正确识别的次数,MC为蒙特卡罗重复试验次数,RMP为正确识别概率的试验估计值。

3.2 仿真实验

单载波常规信号包络谱与包络相关谱仿真分析

在本仿真分析中,设接收机采样率=56 MHz,信号中频频率=70 MHz,符号速率Rs=2 500 kHz,信号采样点数Len=1 048 576,加入SNR为3 dB的高斯白噪声,脉冲成形()采用平方根升余弦,滚降系数=05,调制样式分别为二阶相移键控(binary phase shift keying, BPSK)、四阶相移键控(quadrature phase shift keying，QPSK)、16阶正交幅度调制(sixteen quadrature amplitude modulation, 16QAM)，产生信号并计算其包络谱和包络相关谱,仿真结果如图1所示。

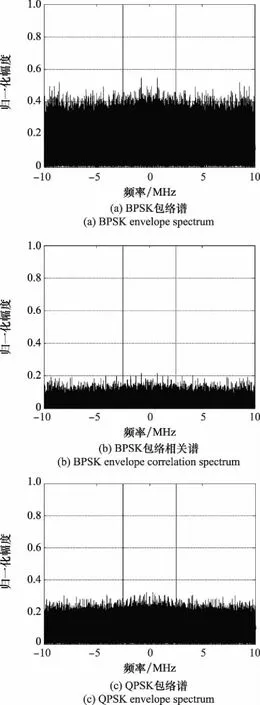
图1 单载波常规信号包络谱与包络相关谱Fig.1 Envelope spectrum and envelope correlation spectrum of single-carrier normal signal

从图1可以发现,对于单载波常规信号,其包络相关谱相比包络谱具有抑制高斯白噪声的作用,而且包络相关谱与包络谱一样,在符号速率频率位置也具有离散的谱线,能够用来估计信号的符号速率。

单载波扩频信号包络谱与包络相关谱仿真分析

在本仿真分析中,设接收机采样率=56 MHz,信号中频频率=70 MHz,符号速率Rs=2 500 kHz,信号采样点数Len=1 048 576,加入SNR=3 dB的高斯白噪声,脉冲成形()采用平方根升余弦,滚降系数=0.5,调制样式分别为BPSK;扩频码类型为序列,扩频码阶数为9,码长为511,产生直接序列扩频(direct sequence spread spectrum, DSSS)信号并计算其包络谱和包络相关谱,仿真结果如图2所示。

3)然后根据判断矩阵的一致性程度与Step2中的聚类分析权重相结合(乘积关系)，求解综合的专家权重，然后对专家权重进行归一化处理。

图2 DSSS信号包络谱与包络相关谱Fig.2 Envelope spectrum and envelope correlation spectrum of DSSS signal

从图2可以发现,对于扩频信号,包络相关谱仍然具有高斯白噪声抑制能力。

多载波FDMA信号包络谱与包络相关谱仿真分析

在本仿真分析中,设接收机采样率=56 MHz,接收机中频频率=70 MHz,子带符号速率Rs=200 kHz,信号采样点数Len=1 048 576,加入SNR=3 dB的高斯白噪声,脉冲成形()采用平方根升余弦,滚降系数=0.5,调制样式分别为BPSK;用户数为20,用户之间频率间隔为450 kHz,产生信号并计算其包络谱和包络相关谱,仿真结果如图3和图4所示。

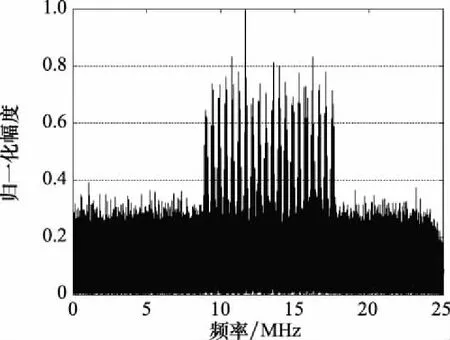
图3 多载波FDMA信号频谱Fig.3 Spectrum of multi-carrier FDMA signal

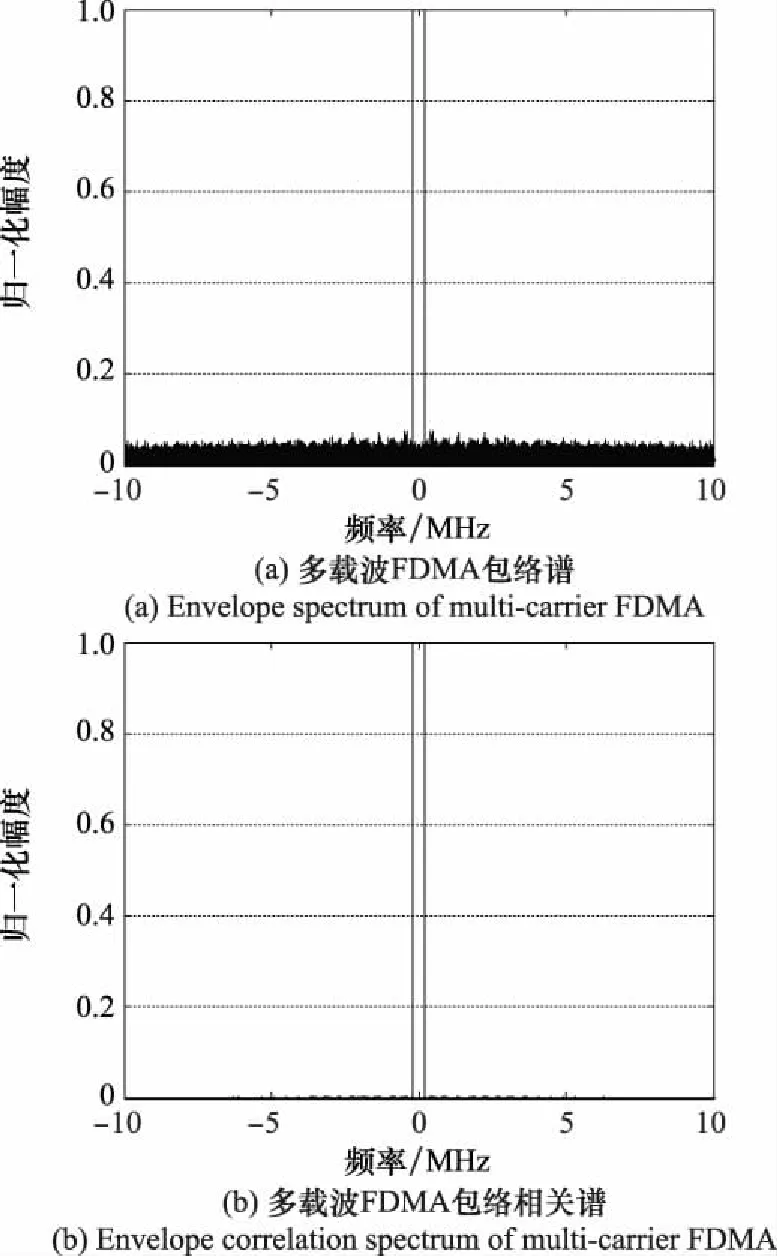
图4 多载波FDMA信号包络谱与包络相关谱Fig.4 Envelope spectrum and envelope correlation spectrum of multi-carrier FDMA signal

从图3可以看出,对于多载波FDMA信号的频谱具有多子带特征,与多载波OFDM信号频谱有些相似。

从图4可以看出,对于多载波FDMA信号,其包络相关谱与单载波信号接近,与多载波OFDM信号区别明显,同时也具有高斯白噪声抑制能力。

多载波OFDM信号包络谱与包络相关谱仿真分析

在本仿真分析中,设接收机采样率=56 MHz,接收机中频频率=70 MHz,符号速率Rs=1 000 kHz,信号采样点数Len=1 048 576,加入SNR=3 dB的高斯白噪声;子载波个数为64,数据子载波数为48,码片时长为0.05 μs,子载波脉冲成形()采用平方根升余弦,滚降系数=0.5,子载波调制样式分别为QPSK,产生信号并计算其包络谱和包络相关谱,仿真结果如图5和图6所示。

图5 多载波OFDM频谱Fig.5 Spectrum of multi-carrier OFDM

图6 多载波OFDM包络谱与包络相关谱Fig.6 Envelope spectrum and envelope correlation spectrum of multi-carrier OFDM

从图5可以看出,对于多载波OFDM信号的频谱具有多子带特征,与多载波FDMA信号频谱有些相似。

从图6可以发现,对于多载波OFDM信号,其包络相关谱与多载波FDMA区别明显,同时相比包络谱具有抑制高斯白噪声的作用,而且包络相关谱与包络谱一样,在子载波的符号速率频率位置也具有离散的谱线,能够用来估计子载波的符号速率。

识别率对比仿真分析

在本仿真分析中,设接收机采样率=56 MHz,接收机中频频率=70 MHz,符号速率Rs=1 000 kHz,信号采样点数Len=1 048 576,加入的高斯白噪声SNR变化范围为-10～10 dB;子载波个数为64,数据子载波数为48,码片时长为0.05 μs,子载波脉冲成形()采用平方根升余弦,滚降系数=0.5,子载波调制样式分别为QPSK,产生多载波OFDM中频采样信号。

用本文基于包络相关谱的方法与基于包络谱、高阶累积量的识别方法分别对OFDM信号进行识别,计算其识别正确率RMP,进行500次蒙特卡罗试验,结果如图7所示。

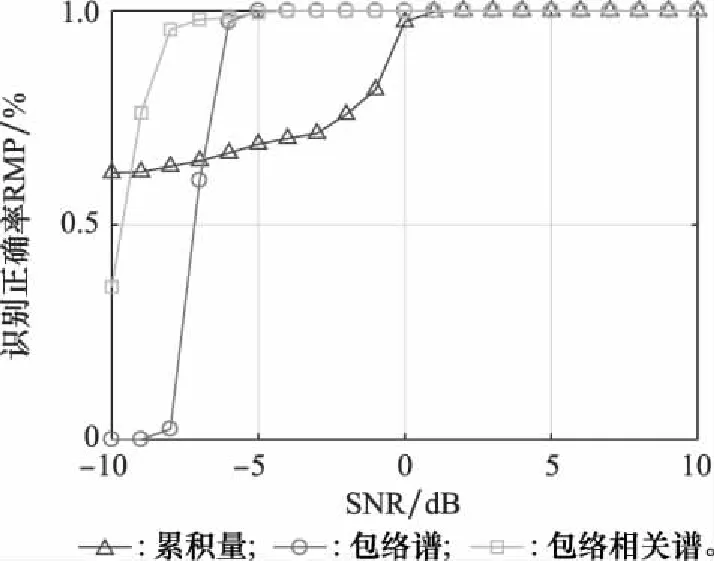
图7 识别率随SNR的变化情况Fig.7 Variation of recognition rate with SNR

从图7可以看出,本文算法在SNR为-9 dB时,识别正确率可以达到90%,比基于包络谱的方法提升了3 dB;本文算法在SNR为-5 dB时,识别正确率可以达到100%,而高阶累积量的方法在0 dB时,才能达到100%;同时,对低SNR环境的适应能力要优于基于高阶累积量的方法6 dB左右。

另外,在多次识别实验时,统计了3种识别算法的平均识别时间,结果如图8所示。

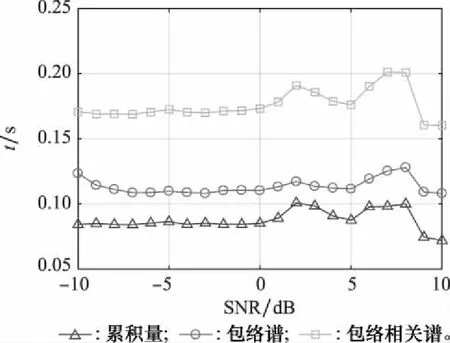
图8 平均识别时间随SNR的变化情况Fig.8 Variation of average time-consuming with SNR

从图8可看出,本文算法在时间复杂度上会有一定的上升,这是因为增加了相关运算,但时效性还是与基于包络特征的识别方法处于一个数量级上。

4 结 论

针对多载波OFDM信号的识别问题,本文提出了一种基于包络相关谱的识别算法。该方法通过检测信号包络相关谱的周期性离散谱线,实现多载波OFDM信号与单载波常规信号及多载FDMA信号的区分,从而完成对OFDM信号的识别。

本文提出的识别算法,由于使用了信号包络相关谱,相比包络谱具有噪声抑制能力,提高了算法在低SNR条件下的识别估计能力。其次,包络相关谱的周期特征不受信号频率影响,相比高阶累积量的识别方法,具体更好的低SNR环境适应能力。仿真结果表明,本文算法的多载波OFDM信号识别性能优于高阶累积量的算法。同时,还能估计OFDM信号的子载波符号速率。