浅谈数学解题的顺推与逆推结合的思考方式

何星泽

【摘要】学生的数学能力如何，数学成绩如何，很大程度上体现在解题能力上，而解题能力的提高最重要的是学会思考，要善于在已知和未知之间搭建起“鹊桥”。本文通过几个例题对解题过程进行分析总结，着重展示如何通过顺推与逆推结合的思考方式搭建“鹊桥”，找到解题的突破口。

【关键词】解题能力;顺推分析;逆推分析

一、发现问题

笔者回顾多年的教育教学工作，发现在学生的学和教师的教等两个方面都存在一些现象：

一是有部分学生上课认真听讲，认真做笔记，课后也认真复习，能按时完成作业，但却考不好，教师讲的一些题目能听懂，但稍作变式就不会了，遇到稍有点难度的题，则显得无从下手。

很多教师把这一类学生总结为“不会学”，但笔者认为这部分学生并不是不会学，而是不会思考，并非智商不高，而是没掌握正确的思考方法，一旦他们学会了正确的思考方法，学会了分析问题，他们的解题水平、数学能力必定能有很大提高.

二是有些教师在解题教学上存在一些现象，不可否认，他们的基本功很扎实，善于题型的归类、方法的总结。然而，有时只是方法的简单堆积或解题技巧的神秘出现，很少从学生思维的起点分析问题，也很少分析“为什么这样解”“是什么促使我这样思考”，没有讲清楚思路的来源与发展的过程。尤其是要作辅助线的问题，当学生问到怎么样才能想到这样作辅助线时，他们的回答常常是“这是一种直觉，题做多了就会了”。可见，有些学生不会思考，和此类教学方式有一定关系。

那么，如何解决上述两种现象呢？

这要求教师和学生都要掌握正确、高效的思考方法（模式）。在解题时，一般的思考模式是：读题→弄清题干给了哪些条件→分析这些条件与问题之间的联系→拟定解题计划，这种思考模式一般称为顺推分析，相当于从起点瞭望终点;另外，也有逆向思考模式，即從终点回望起点，先从问题入手，通过假定问题已经被解决来分析到底需要哪些条件，这种思考模式一般称为逆推分析。

笔者认为，顺推与逆推结合的思考方式会更为常见，简言之就是：由已知看可知，从未知看需知。它能缩短已知和未知之间的距离，而且往往能做到一题多解。

二、顺推与逆推结合的思考方式的步骤

大体上有三个步骤：

（1）顺推分析：从已知条件往后推，看每一个已知能得到什么小结论，把不同的已知（有时需要与小结论）组合起来思考，看又能得到什么小结论。

（2）逆推分析：从所求（未知结论或问题）往前推，看要解决这个问题需要什么条件，有时是把所求进行等价转化。

（3）在（1）中的小结论和（2）中所需条件（或等价转化后的问题）之间找到契合点，建立联系，实现解题的突破。

有时需要重复（1）（2）（3）才能有所进展。在某些代数题中，（1）和（2）有时可以交换顺序。这个过程可以有一个浪漫的比喻，有点像牛郎织女的鹊桥相会，已知条件好比是牛郎，所求（未知结论或问题）则是织女，寻找解题思路的过程就相当于为牛郎织女搭建鹊桥的过程，鹊桥建好了，题就能解出来。而利用顺推和逆推结合的思考方式在搭建已知和未知的“鹊桥”时具有独特的优势与魅力。

三、顺推和逆推结合的思考方式的例题研究

我们先看一道最近网课学习中遇到的习题：

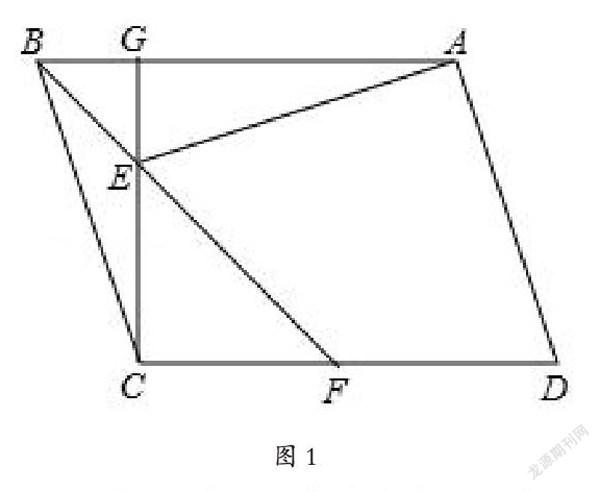
例1：如图1，平行四边形ABCD中，CG⊥AB于点G，∠ABF=45°，F在CD上，BF交CD于点E，连接AE，AE⊥AD。求证：CE+BE=AB.

按照顺推和逆推结合的思考方式有如下分析：

（1）顺推分析：由ABCD是平行四边形，CG⊥AB，∠ABF=45°可以得到△BEG和△FCE都是等腰直角三角形，所以BG=EG，CE=CF;由AE⊥AD得AE⊥BC.这些小结论如何进一步使用就要结合下一步的分析;

（2）逆推分析：CE+BE=AB，有点类似于两条线段的和（差）等于第三条线段的形式，常用的方法是截长补短，如何对BE进行转化则是本题的难点，对它的不同的转化方式就会产生不同的解题方法。

BE可以有两种转化方式：

①根据等腰直角三角形的三边关系，BE=BG+EG，于是所证结论可以等价转化为CE+BG+EG=AB，即CG+BG =AB，即只需证CG=AG.

②构造BE为直角边的等腰直角三角形，BE就是斜边的长。

（3）找到（1）中的小结论与（2）中转化后的问题之间的关系，完成解题，具体方法如下：

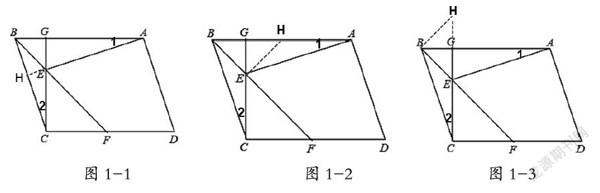
对于（2）①的分析，可延长AE交BC于H（如图1-1），可得∠1=∠2，易证△BGC≌△EGA，于是CG=AG，已知与未知完美结合，进一步即得CE+BE=AB.

对于（2）②的分析，过E作EH⊥BE交AB于H（如图1-2），知△BEH是等腰直角三角形，则BE=BH，于是只需证CE=AH，即证△BEC≌△EHA即可.

这是采用截长法证明，还可以用补短法证明。

过B作BH⊥BE交CG的延长线于H（如图1-3），则BE=EH，于是只需证CH=AB，即证△BCH≌△EAB即可。

以上三种方法都是顺推与逆推结合的思考方式的很好例子，有顺推才能发挥已知条件的作用，有逆推才能知道目标在哪，问题的本质是什么，已知条件怎么样才能更好地使用。尤其在逆推时，不同的转化方法起到了一题多解的效果，对开拓学生的思维大有裨益。

现在，我们用这种方法再分析一道中考题：

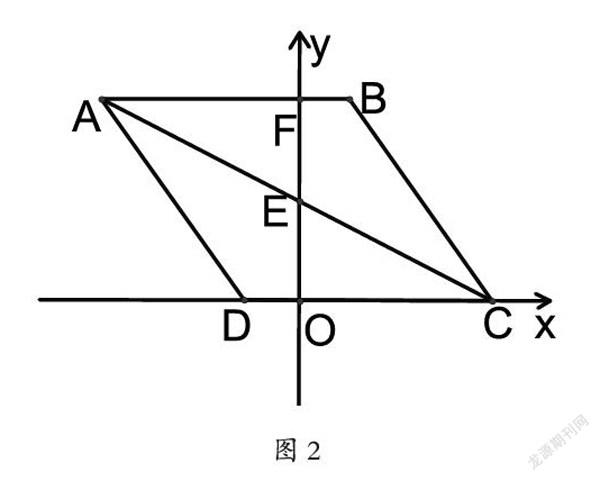
例2：如图2，O为坐标原点，四边形ABCD是菱形，A（-8，8），B点在第一象限，AB=10，AB与y轴交于点F，对角线AC交y轴于点E.

（1）直接写出B、C点的坐标。

（2）动点P从C点出发以每秒2个单位的速度沿折线段C—D—A运动，设运动时间为t秒，请用含t的代数式表示△EDP的面积。

（3）在（2）的条件下，是否存在一点P，使△APE沿其一边翻折构成的四边形是菱形，若存在，请直接写出当t为多少秒时存在符合条件的点P;若不存在，请说明理由。

第（3）问按照顺推和逆推结合的思考方式有如下分析：

（1）顺推分析可以得到OD=BF=2，AF=CO=8，可证△AEF≌△CEO得EF=EO=4，AE=EC=4.

（2）逆推分析：这是个菱形存在性问题，而菱形的一条对角线可把菱形分成两个全等的等腰三角形，所以这个问题可以等价转化为等腰三角形的存在性问题。

（3）找到前两步的契合点，搭建“鹊桥”，完成解题。根据两个定点一个动点构成等腰三角形的方法——两圆一线，确定点P的位置，再结合数据计算t的值，具体过程如下：

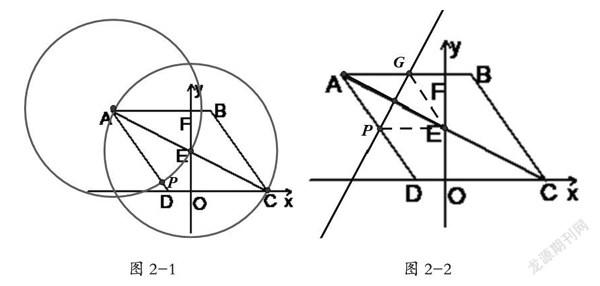
①AE=AP时（如图2-1，以A为圆心AE为半径作圆交AD于P），可知AP=4，则t=10-2。

②当EA=EP时（如图2-1，以E为圆心AE为半径作圆），此时A、P、E不能构成三角形，舍去。

③当PA=PE时，作AE的垂直平分线交AB于G，交AD于P（如图2-2），易证四边形APEG是菱形，设AP=AG=GE=x，GF=8-x，在Rt△GFE中，由勾股定理得x2=42+（8-x）2，解得x=5，进而求得t=7.5;

综上，存在t=10-2或7.5秒时，△APE沿其一边翻折构成的四边形是菱形。

这个问题的解答也体现了顺推和逆推结合的思考方式的价值，尤其是逆推分析把菱形问题转化为等腰三角形问题，化新知识为旧知识，简化了思考过程，能迅速找到解题的突破口，体现了数学的转化与化归思想。

顺推与逆推结合的思考方式不仅适用于几何问题，在一些代数问题中也十分实用，请看下题：

例3：a，b，c，x都是实数，并且a

x-c的最小值。

此题可以采用零点分段法对x的取值分类讨论，分别去掉绝对值符号，最后比较各段的值，再取最小值;也可以分段之后画出函数图像，取最低点的函数值，但这些方法都必须经历复杂的去绝对值符号的过程，有没有更简单的方法呢？

由于此题已知条件比较简单，顺推分析有点漫无目的，我们可先作逆推分析，则会发现 x-a 可以表示数轴上点x到点a之间的距离，x-a+x-b+x-c就表示点x到点a，b，c的距离之和，逆推与顺推结合，可以画出图3：

显然，这三条线段没有重叠部分时，和最小，此时x=b，这最小和为点a，c的距离，为 a-c =c-a.

这种方法还能推广到有n个点的情况。可见，对所求问题作适当的转化是多么的重要，恰到好处的逆推分析大大地简化的解题过程，而且获得了非常巧妙的解法。学生在这个过程中也会体验到解题的乐趣，继而加大学习数学的信心。

我们再看一道代数求值题：

例4：已知a=+，b=-，求的值。

这个题直接代数当然可以求解，但是显然不是好方法。已知条件比较简单，顺推需结合逆推才能进行，于是，先逆推分析对所求变形，，此时如果带入数据也可以，但仍然不是最好的方法，结合已知，需进一步变形：，此时可以顺推计算a+b=2，ab=1，再代入上式求值则非常简单。

诚然，不是所有题都需要（或都适合）用顺推与逆推结合的思考方式，有的题直接用顺推或逆推就能解答，但掌握顺推与逆推结合的思考方式无疑是有益的。

从上面四道题的演示，我们可以体会到，如果學生能够养成顺推与逆推结合来思考问题的习惯，那么在解决数学问题的时候不仅知道已知条件有什么用，还能知道最终目标在哪，缩短了从已知到达未知的过程，而且往往会有一题多解的收获，既能开拓思维，还能培养兴趣，非常有利于数学能力的提高。

四、顺推与逆推结合的思考方式的培养

学生的思维习惯受多方面因素的影响，如，学生自身的特质、从小的成长环境和父母的思维的方式、教师的教育等。具体可以从教与学两个方面来培养：首先，教师要有顺推与逆推结合的思考方式，平时解题时就要体会这种思维方式的魅力，感受由此带来的解题成功的喜悦与乐趣。在解题教学时，教师更要善于引导学生这样去思考，让学生自己体会到这种喜悦与乐趣，他们才会乐于这样去思考;其次，学生也要有养成这种思考方式的意识。对于平时的作业题如果发现单纯的顺推和逆推分析不行时，就应想到顺推和逆推结合来思考问题，模仿教师平时讲题的思维方式来解题;再次，教师要引导学生养成回顾的习惯。波利亚在《怎样解题》中总结的解题四步骤中的第四步就是回顾。回顾既是检查是否有错误，又是对解题过程的优化。体会一下思路是如何产生的，是哪个已知条件起到了突破性的作用，以后遇到这种条件时是不是还可以这样用;这种解题方法在以前哪道题曾经见过，能不能推广到这一类题。这样，新的知识技能纳入到旧知识体系中，从而拓展旧知。假以时日，学生的良好思维品质必然能养成，数学能力一定可以提高。

参考文献：

[1]杨彬.中学数学解题时的逆向思考方式[J].数学参谋，2020（2）.

[2]（美）G·波利亚.怎样解题[M].涂泓，冯承天，译.上海科技教育出版社，2011.

责任编辑  陈  洋

2348501705386