基于累积损伤的渗碳齿轮钢疲劳寿命预测模型构建*

邓海龙 刘 兵 郭 扬 康贺铭 李明凯 李永平

(①内蒙古工业大学机械工程学院，内蒙古 呼和浩特010051;②内蒙古自治区先进制造技术重点实验室，内蒙古 呼和浩特010051)

齿轮钢有强度高，耐磨性好，抗腐蚀性强等优点，被广泛应用于工程机械、农业机械和汽车工业等领域。随着现代科技的飞速发展，机械设备在满足功能需求的同时，人们对其服役期间的安全可靠性有了更高的期待。在工程实际中，由各类齿轮钢制成的机械零部件发生疲劳失效的行为比比皆是[1-2]。因此，研究齿轮钢的疲劳特性对确保机械产品在服役期间的安全可靠性具有重要意义。

齿轮钢的疲劳寿命受材料本质[3](如微观组织、力学性能和缺陷尺寸等)、工作条件[4-5](如加载频率、施加应力及应力比等)和外部环境[6](如温度等)等因素的影响，常呈现出双S-N曲线的现象。对于超高周体系的内部失效，疲劳裂纹通常由内部缺陷(如气孔、非金属夹杂和不均匀组织等)引起的[7-8]。其中夹杂是诱发齿轮钢超高周疲劳失效的主要原因[9]。作为内部失效的典型特征，鱼眼常呈现在疲劳断口表面。此外，在夹杂周围发现一片颗粒形成白亮粗糙区域，这就是所谓的FGA[10]。研究表明，FGA形成所消耗的寿命占据了齿轮钢疲劳全寿命的90%以上[11]。因此，FGA的尺寸对疲劳寿命预测模型的构建十分重要。

基于疲劳失效的断裂特征，一些齿轮钢的疲劳寿命预测模型被提出或修正。Murakami Y基于维氏硬度和缺陷尺寸提出了疲劳极限评估模型[12]。Wang Q Y等人通过引入疲劳寿命改进了Murakami Y提出的模型中的常数，提出了修正的疲劳寿命预测模型[13]。Sun C Q等人基于累积损伤法提出了考虑夹杂尺寸和FGA尺寸的模型用于预测夹杂-FGA-鱼眼型失效的疲劳寿命[14]。基于Kachanov损伤定律，Hou S Q等人建立了考虑平均应力和应力比的疲劳寿命预测模型[15]。齿轮钢的失效过程分为疲劳裂纹的萌生和扩展，上述研究大多局限于考虑疲劳裂纹萌生过程或扩展过程建立疲劳寿命预测模型且未考虑最大应力和残余应力。因此，建立疲劳裂纹萌生及扩展行为且考虑残余应力和最大应力的疲劳寿命预测模型能更好地诠释齿轮钢的疲劳特性。

本文旨在探究变应力比下渗碳齿轮钢在长寿命体系中的疲劳性能。通过对S-N曲线特征、破坏机制、裂纹特征尺寸和残余应力分布的分析，建立了基于累积损伤法的裂纹萌生和扩展寿命预测模型。最终基于平均夹杂尺寸建立了渗碳齿轮钢的疲劳全寿命预测模型。

1 材料及实验

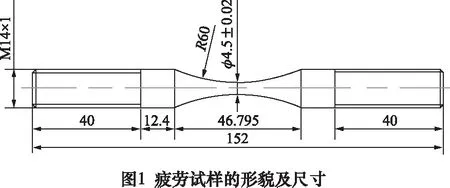
本文中试验材料为齿轮钢，其化学成分(质量百分比)列于表1中。将初始棒料加工成标准疲劳拉伸试样，随后将试样置于真空渗碳炉中进行渗碳处理：在930 ℃下碳势为1.1%的渗碳炉中渗碳5 h，随后空冷至室温。紧接着对试样进行热处理工艺:830 ℃油淬×45 min+160 ℃空气回火×2 h。最终疲劳试样的外观形貌及特征尺寸如图1所示。

表1 齿轮钢的化学成分 %

轴向加载疲劳试验在QBG-100KN疲劳试验机上进行，试验环境为室温，加载频率为100 Hz。施加的应力比R分别为0和0.3，其中R= 0时施加的应力幅间隔为25 MPa，R=0.3时应力幅间隔为17.5 MPa。基于扫描电镜(SEM)对断口形貌及裂纹尺寸进行观测。利用连续刚度测量方法，使用纳米压头G200测量渗碳齿轮钢的微观硬度，沿半径方向每隔100 μm测试一次。基于TEC4000 x射线衍射系统，测量渗碳齿轮钢从表面到内部的残余应力值。

2 结果及讨论

2.1 力学性能及S-N曲线

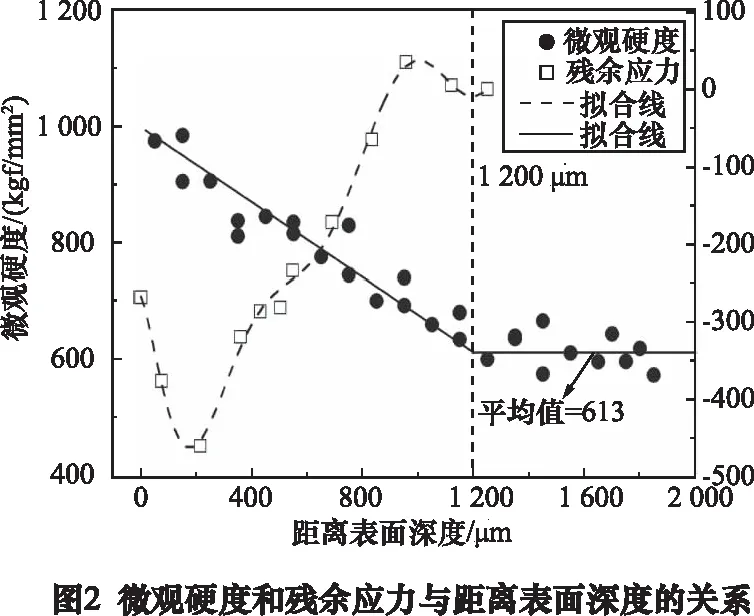
渗碳齿轮钢的抗拉强度为1 780 MPa，微观硬度和残余应力如图2所示。由图可知，渗碳齿轮钢的硬度值随着距离表面深度的增大而降低，而残余应力值随着距离表面深度的增加呈现先减小后增加的现象。由微观硬度和残余应力的变化规律可知，渗碳层的深度约为1 200 μm。经多项式拟合，可得渗碳层内残余应力随距离表面深度的关系为

σr=-267.23-0.89x-0.018x2+1.73×10-4x3-5.73×10-7x4+9.57×10-10x5-8.58×10-13x6+3.59×10-16x7-7.31×10-20x8

(1)

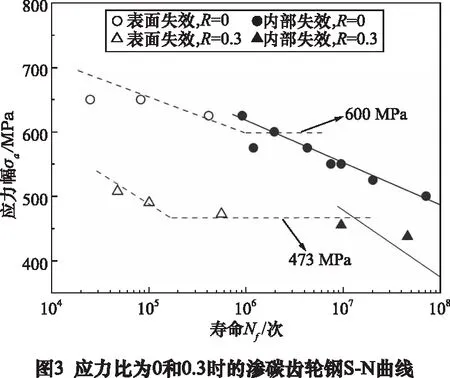
本次疲劳试验获得的渗碳齿轮钢的S-N曲线如图3所示。两种应力比的寿命分布在104～108之间，均没有出现传统的疲劳极限。根据疲劳裂纹萌生位置的差异，可以将两种应力比下的疲劳失效模式分为表面失效和内部失效，并分别用空心图标和实心图标表示，虚线和实线表示绘制的S-N曲线。虚线的水平部分表示表面疲劳极限，应力比为0和0.3对应的表面疲劳极限分别为600 MPa和473 MPa。本文中将108个循环次数对应的疲劳强度定义为渗碳齿轮钢的疲劳极限。基于线性拟合，应力比为0和0.3的疲劳极限值为490 MPa和374 MPa。从整体上看，渗碳齿轮钢的S-N曲线呈现不断下降的趋势，且在相同寿命下R=0的疲劳强度大于R=0.3的。

2.2 断口形貌及裂纹尺寸

利用SEM对所有疲劳失效断口形貌进行了观测，一些具有代表性的形貌如图4所示。根据疲劳裂纹萌生位置，将疲劳失效形式分为内部失效和表面失效，内部失效伴有FGA的存在，表面失效伴有表面光滑区(surface smooth area, SSA)的存在。由内部失效的断口裂纹特征(图4b,4f)可知，夹杂周围裂纹萌生区呈现出细小光亮的颗粒状裂纹，这就是所谓的FGA。之后在循环载荷和残余应力的共同作用下疲劳裂纹进入稳定扩展阶段，裂纹呈现出放射型特征，构成了内部失效的典型断口特征-鱼眼。由表面失效断口裂纹特征(图4c,4d)可知，由循环载荷和残余应力造成的应力集中使夹杂周围的裂纹向内部稳定扩展，形成了SSA。之后疲劳裂纹扩展迅速，形成了表面粗糙区(surface rough area, SRA)，这片区域发现许多平坦的小刻面，小刻面上的裂纹较短且周围有撕裂棱特征。

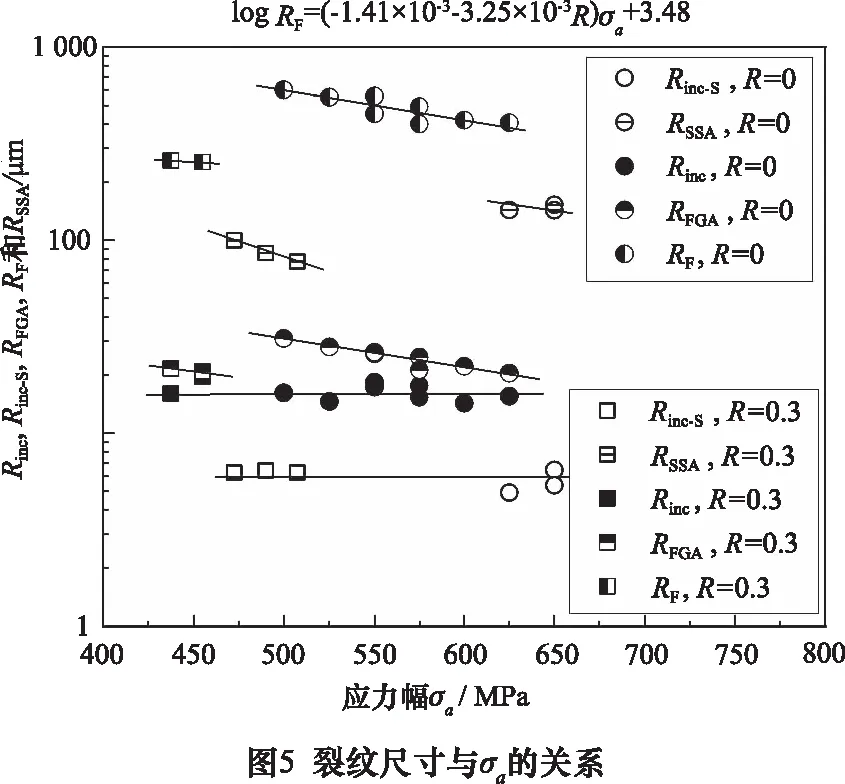
由于内部夹杂、FGA、鱼眼、表面夹杂、SSA的形状近似于圆形，分别采用Rinc、RFGA、RF、Rinc-S、RSSA表示它们的半径，其尺寸如图5所示。由图可知，内部引发疲劳裂纹的夹杂尺寸相差不大，均值为16.50 μm。同样地，表面夹杂尺寸也相差不大，均值为5.94 μm。据此可知夹杂尺寸与施加的应力幅、应力比及疲劳寿命无关，只与齿轮钢的熔炼工艺相关。随着施加应力幅值的增加，FGA、鱼眼及SSA的尺寸均有减小的趋势。基于最小二乘法，可分别得到内部失效时FGA尺寸和鱼眼尺寸与应力比和应力幅之间的关系

logRFGA=(-1.44×10-3-1.75×10-3R)σa+2.20

(2)

logRF=(-1.41×10-3-3.25×10-3R)σa+3.48

(3)

3 齿轮钢疲劳寿命预测模型构建

3.1 疲劳寿命评估方法构建

渗碳齿轮钢内部失效过程分为裂纹萌生和裂纹扩展。基于裂纹的萌生和扩展都是由施加的循环载荷引起的事实，假设每次对试样施加循环载荷，都会导致试样内部裂纹的萌生或扩展。因此，基于累积损伤理论，建立以下关系式

(4)

式中:RN为第n次循环加载后的裂纹萌生或扩展长度，Rs为裂纹萌生或扩展前的裂纹初始尺寸，Rf为裂纹萌生或扩展结束后的最终裂纹尺寸，pn为第n次循环加载后的裂纹萌生或扩展形成的损伤区域半径增量与第n-1次加载后的总损伤区域半径的比值。为简化式(4)，引入与裂纹萌生或扩展速率和寿命相关的变量p，建立以下关系

(5)

因此，将式(5)整理后代入式(4)，并对公式两端进行对数运算，整理可得N的近似解为

(6)

在超高中体系中，裂纹扩展速率非常慢，故p值趋近于0。因此，式(6)可以被改写为

(7)

对于未经表面强化处理的材料，疲劳裂纹萌生和扩展速率与抗拉强度有关[16]。而对于渗碳齿轮钢，裂纹萌生及扩展速率还与表面处理引起的残余应力和施加的最大应力息息相关。残余应力会抑制或促进内部疲劳裂纹的萌生和扩展[17]，因此，考虑残余应力分布和最大应力对构建渗碳齿轮钢疲劳裂纹寿命预测模型十分重要。据此，建立以下关系式

(8)

式中：σmax表示最大应力。将式(8)代入式(7)中，同时为使建立的疲劳裂纹萌生或扩展寿命预测模型更精确，引入拟合常数m和n。因此，可将式(7)改写为

(9)

结合最大应力，应力幅和应力比的关系，整理可得基于累积损伤法的寿命评估方法为

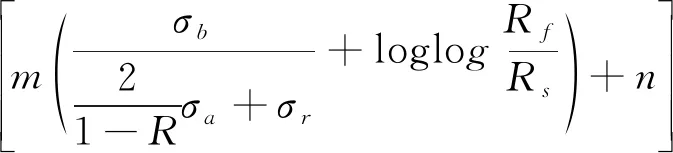
(10)

3.2 裂纹萌生及扩展寿命预测模型

由于FGA内的裂纹成形属于萌生阶段，故FGA的尺寸是预测渗碳齿轮钢疲劳裂纹萌生寿命的重要参数。因此，将夹杂尺寸定义为初始裂纹尺寸，将FGA尺寸定义为疲劳裂纹萌生结束尺寸，将其代入式(10)中可得渗碳齿轮钢的疲劳裂纹萌生寿命预测模型为

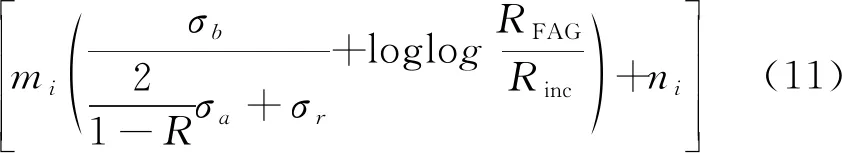
裂纹扩展阶段分为稳定扩展和不稳定扩展，且分别对应鱼眼之内和之外的裂纹。由于鱼眼之外裂纹扩展迅速，所消耗的寿命极少，所以本文只考虑了裂纹稳定扩展阶段所消耗的寿命。因此，将FGA尺寸定义为裂纹扩展前初始裂纹尺寸，将鱼眼尺寸定义为疲劳裂纹稳定扩展结束尺寸。将两种裂纹尺寸分别代入式(10)中可得渗碳齿轮钢的疲劳裂纹扩展寿命预测模型为

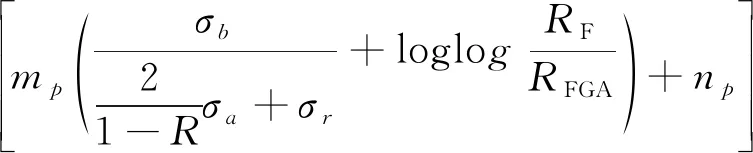
(12)

3.3 渗碳齿轮钢全寿命预测模型

基于式(11)及式(12)，最终渗碳齿轮钢内部失效全寿命预测模型为

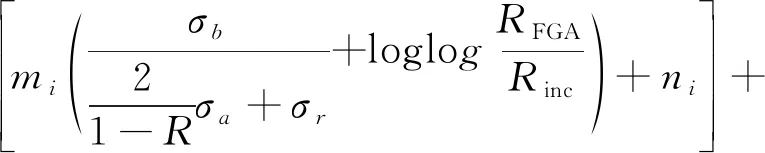
NT表示渗碳齿轮钢完全失效后所消耗的疲劳总寿命。基于试验数据及最大继承法，可得到mi、ni、mp和np的值，如表2所示，预测的疲劳寿命与试验所获得的寿命比值如表3所示。由表可知，预测结果较为精确。

表2 全寿命预测模型拟合参数评估

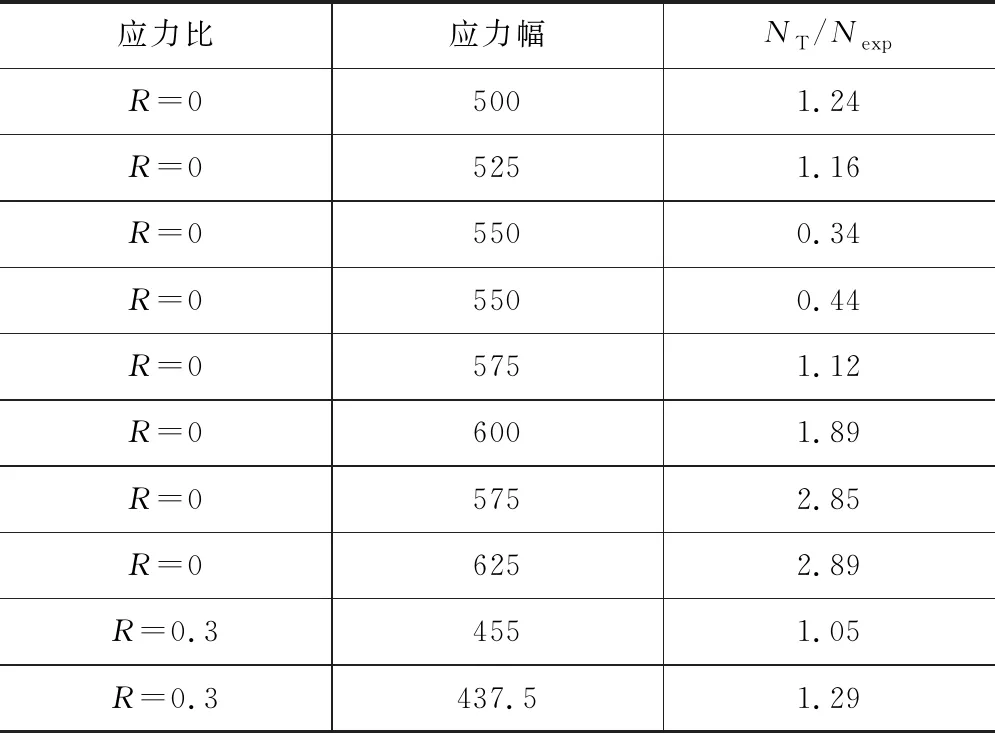
表3 疲劳寿命预测结果

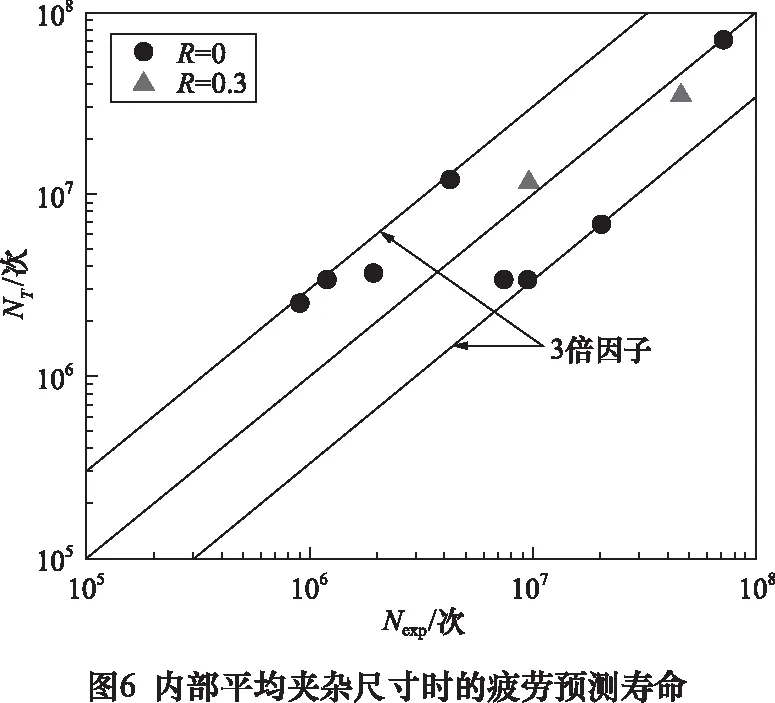
众所周知，齿轮钢的疲劳寿命与内部夹杂尺寸有关。由于夹杂尺寸与应力比和应力幅无关，因此将内部夹杂平均尺寸(Rinc=16.50 μm)代入式(13)中，可得渗碳齿轮钢的预测疲劳寿命NT与试验寿命Nexp关系，如图6所示。由图可知，预测的疲劳寿命较为精确且在3倍因子以内。因此，本文建立的渗碳齿轮钢全寿命疲劳寿命预测模型可以被接受。

4 结语

为探究渗碳齿轮钢的疲劳性能，在室温下进行了超高周疲劳试验，得到的结论如下：

(1) 通过对断口形貌的观测，将内部疲劳失效分为3个阶段：裂纹萌生阶段(夹杂-FGA)内、裂纹稳定扩展阶段(FGA-鱼眼)和瞬间断裂(鱼眼外)。

(2) 基于累积损伤法，建立了虑及残余应力的渗碳齿轮钢疲劳裂纹萌生和扩展寿命预测模型。

(3) 基于平均裂纹尺寸，建立了渗碳齿轮钢超高周疲劳全寿命预测模型，精确度较高。