谈谈近年来高考压轴题中导数综合应用问题的解决策略——以解析式中含有ex,lnx 为例

张雪丽

(安徽省萧城一中)

导数的综合应用问题是高考的必选题,基本上出现在第20或21题,难度较大,能拉开区分度.这类考题一般围绕y＝ex,y＝lnx与其他初等函数,综合考查函数的单调性、最值、零点、极值点、恒成立等,技巧性高、综合性强,更能充分考查学生的数学抽象、直观想象、逻辑推理、数学建模等核心素养,彰显学生思维的灵活性及多样性.近5年来高考全国卷的14份考卷中有10份涉及ex或lnx函数模型,下面结合几道典型的高考题说明这类导数综合应用问题的解决策略.

1 含有ex 的函数模型构造法

例1(2018年全国Ⅱ卷理21)已知函数f(x)＝ex－ax2.

(1)若a＝1,证明:当x≥0时f(x)≥1;

(2)若f(x)在(0,＋∞)只有一个零点,求a.

(1)略.

(2)方法1直接利用原函数模型

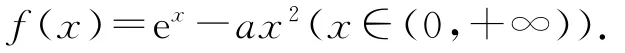
当a≤0时,f(x)＞0恒成立,所以f(x)在(0,＋∞)上无零点.

当a＞0时,f′(x)＝ex－2ax,再次求导可得

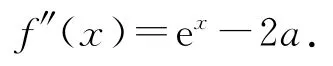
从而 当x∈(0,ln2a)时,f″(x)＜0,当x∈(ln2a,＋∞)时,f″(x)＞0,所以f′(x)在(0,ln2a)上单调递减,在(ln2a,＋∞)上单调递增.

当x＝ln2a时,有

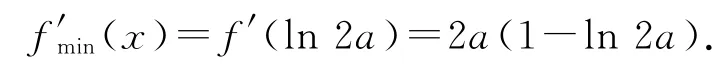
当1－ln2a＞0,即a＜时,f′(x)＞0,即f(x)在(0,＋∞)上单调递增,且f(0)＝1,从而f(x)无零点,所以1－ln2a＜0,f′(ln2a)＜0.

又因为f′(0)＝1＞0,所以存在x0∈(0,ln2a)使f′(x0)＝0,从而当x∈(0,x0)时,f′(x)＞0,当x∈(x0,ln2a)时,f′(x)＜0.又因为＞0,所以存在x1＞ln2a,使f′(x1)＝0,即ex1－2ax1＝0.从而当x∈(x0,x1)时,f′(x)＜0.

当x∈(0,x0)或(x1,＋∞)时,f′(x)＞0,所以函数f(x)在(x0,x1)上单调递减,在(0,x0),(x1,＋∞)上单调递增.

然而,端点值f(0)＝1,极小值f(x1)＝ex1－,所以f(x)有唯一的零点x1,即ex1－＝0,结合ex1－2ax1＝0,可以求得x1＝2,a＝.

方法2 构造成“常数＋因式·et”型.

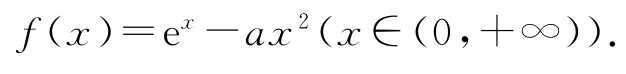
构造函数h(x)＝＝1－ax2e－x(x∈(0,＋∞)).f(x)在(0,＋∞)上只有一个零点⇔h(x)在(0,＋∞)上只有一个零点,接着研究h(x)＝1－ax2e－x.

当a≤0时,h(x)＞0,h(x)没有零点.

当a＞0时,h′(x)＝e－xax(x－2).当x∈(0,2)时,h′(x)＜0;当x∈(2,＋∞)时,h′(x)＞0,所以h(x)在(0,2)上单调递减,在(2,＋∞)上单调递增,故h(2)＝1－是h(x)在(0,＋∞)上的最小值.

若h(2)＞0,即a＜,则h(x)在(0,＋∞)上没有零点;若h(2)＝0,即a＝,则h(x)在(0,＋∞)上只有一个零点;若h(2)＜0,即a＞,因为h(0)＝1＞0,所以h(x)在(0,2)上有一个零点.

由(1)知,当x＞0时,ex＞x2,所以

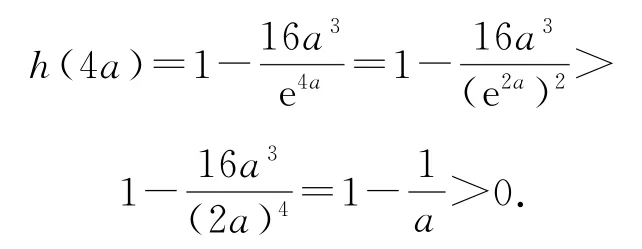
故h(x)在(2,4a)上有一个零点,因此h(x)在(0,＋∞)上有两个零点.

综上,f(x)在(0,＋∞)上只有一个零点时,a＝

方法3分离参数构造函数模型

因为f(x)＝ex－ax2在(0,＋∞)上只有一个零点,所以方程ex－ax2＝0在(0,＋∞)上只有一个解,等价于＝a在(0,＋∞)上只有一个根.

含有ex的函数模型常用的构造方法如下,1)直接利用原函数,有时也可分为两个初等函数模型;2)构造成“常数＋因式·et”型,求导后的运算不易受ex的干扰;3)分离参数法构造函数模型,没有参数,避免了分类讨论,但是有时函数较复杂需多次求导.本题考查了导数与原函数的关系、函数的单调性、零点等知识,涉及函数与方程思想、隐零点问题,考查学生的逻辑推理能力、运算能力、转化能力、数形结合能力等.

2 含有lnx 的函数模型“独立与不独立”法

例2(2017年全国Ⅱ卷21)已知函数f(x)＝ax2－ax－xlnx,且f(x)≥0.

(1)求a;

(2)证明:f(x)存在唯一的极大值点x0,且e－2＜f(x0)＜2－2.

(1)f(x)＝x(ax－a－lnx),因为x∈(0,＋∞),所以f(x)≥0,即ax－a－lnx≥0恒成立.直接构造函数g(x)＝ax－a－lnx,从而

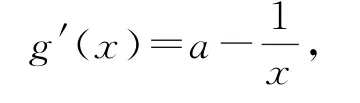
分a≥0,a＜0两种情况讨论,求得a＝1.

(2)利用条件f(x)存在唯一的极大值点x0,一次求导f′(x)＝2x－2－lnx,两次求导可得

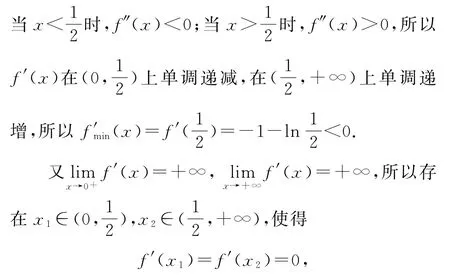
所以函数f′(x)在(0,x1),(x2,＋∞)上单调递增,在(x1,x2)上单调递减,所以f(x)的唯一的极大值点为x1.

故f′(x0)＝2x0－2－lnx0,从而

综上,e－2＜f(x0)＜2－2.

消掉x使lnx的系数为常数,即“独立”lnx,可一次求导解决单调性问题;当lnx的系数不能消掉时,即lnx“不独立”,需两次求导,才能依次推导出单调性、零点、极值点等问题.本题考查了转化的思想、分类讨论的思想,也考查了学生逻辑推理、数学运算、数学建模等核心素养.

变式(2018年全国Ⅲ卷理21)已知函数

(1)若a＝0,证明:当－1＜x＜0时,f(x)＜0;当x＞0时,f(x)＞0;

(2)若x＝0是f(x)的极大值点,求a.本题解析式复杂,难度较大,仍然可以用例2的两种方法,独立lnx一次求导,得到可解的不等式或方程.此方法对于含lnx的函数模型解决如鱼得水.

总之,以y＝ex,y＝lnx为载体,融合其他初等函数的导数综合应用问题,千姿百态、形式不同的表象背后,应归纳研究出解答它们的一般路径和方法,使后续类似的探究有序可循、思维有法可依,避免学习过程中的盲目性,进而培养学生的整体性思维,这可谓由一棵树木,看到整片森林.

(完)