对2020年全国高中数学联合竞赛第4题的多视角探究

李 勇

(贵州省贵阳市息烽县第一中学)

复数虽然在高中教材中讲得简单,在高考中考得也简单,但在竞赛中试题难度比较大,综合性比较强,它往往会与向量、函数、方程、不等式、几何意义等知识综合.解决此类问题常常需要将问题转化为函数、不等式、解析几何的一些几何意义来解答.本文以2020年全国高中数学联合竞赛第4题为例,从9种不同的视角探究这一类问题的解题策略.

1 试题呈现

题目设Z为复数,若为实数(i为虚数单位),则|Z＋3|的最小值为________.

2 命题背景

1)复数的加法、减法、乘法、除法,复数为实数的条件、复数的模长.

2)函数、方程、不等式、几何意义.

3 试题分析

本题是一道典型的复数与其他知识综合的问题,涉及的知识面广,有方程与函数、方程与不等式、方程的几何意义(点到直线的距离、两点间的距离)等,是一道关系错综复杂的动态问题.

4 解法探究

视角1由方程a＋2b－2＝0的特点联想到等差数列的等差中项,故先借助等差数列把a,b用公差d表示出来,然后将其代入得到一个以d为自变量的二次函数,最后求这个二次函数的最小值即可.

解法1消元(等差数列)→二次函数

由a＋2b－2＝0,得a＋2b＝2,则a,1,2b成等差数列.

设公差为d(d∈R),则a＝1－d,b＝所以

视角2根据方程a＋2b－2＝0,可用b把a表示出来,再将其代入中消去a,使得目标变成了一个以b为自变量的二次函数,最后求出这个二次函数的最小值即可.

解法2消元→二次函数

由a＋2b－2＝0,可得a＝2－2b,所以

视角3根据方程a＋2b－2＝0,可用b把a表示出来,再将其代入中消去a,然后构造一个基本不等式的模型,最后用基本不等式即可求出|Z＋3|的最小值.

解法3消元→基本不等式

由a＋2b＝2,可得a＝2－2b,所以

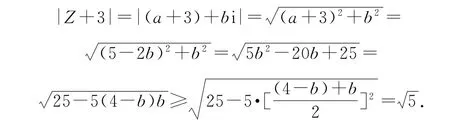
当且仅当4－b＝b,即b＝2时,|Z＋3|取得最小值

视角4根据方程a＋2b－2＝0,可用b把a表示出来,再将其代入中消去a,然后构造一个权方和不等式模型,从而求出|Z＋3|的最小值.

解法4消元→权方和不等式

由a＋2b＝2,可得a＝2－2b,所以

视角5直接由构造一个权方和不等式模型,从而求出|Z＋3|的最小值.

解法5权方和不等式

由a＋2b－2＝0,可得a＋2b＝2,所以

视角6直接由构造一个柯西不等式模型,从而求出|Z＋3|的最小值.

解法6柯西不等式

由a＋2b－2＝0,可得a＋2b＝2,所以

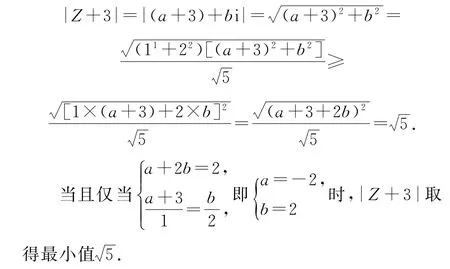
视角7由方程a＋2b－2＝0的特点联想到直线的参数方程,先将a,b用参数t表示出来,然后将其代入中消去a,b,得到一个以参数t为自变量的二次函数,最后求二次函数的最小值即可.

解法7直线参数方程→二次函数

解法8圆的参数方程→三角函数

视角9由的特点联想到两点之间的距离公式,表示平面直角坐标系aOb内的定点(－3,0)与直线a＋2b－2＝0上的动点(a,b)间的距离,求|Z＋3|的最小值,即求定点(－3,0)与直线a＋2b－2＝0上的动点(a,b)之间距离的最小值,易知当定点(－3,0)与直线a＋2b－2＝0上的动点(a,b)的连线垂直于直线a＋2b－2＝0时,距离最小,最后由点到直线的距离公式即可求出|Z＋3|的最小值.

解法9几何意义

由|Z＋3|＝|(a＋3)＋bi|＝,则|Z＋3|表示平面直角坐标系aOb内的定点(－3,0)与直线a＋2b－2＝0上的动点(a,b)间的距离,如图1所示.

图1

易知当定点(－3,0)与直线a＋2b－2＝0上的动点(a,b)的连线垂直于直线a＋2b－2＝0时,距离最小.由点到直线的距离公式得|Z＋3|的最小值为

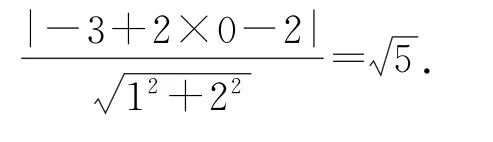
5 反思

从多角度探究一道试题,是培养学生能力的重要方式,是实现数学核心素养的一个重要的载体.多角度探究一道试题有利于学生由点到面的掌握有关知识,有利于学生抓住问题的本质、求解方法以及蕴含的结论,最终实现做一题得一类题,做一题掌握更多的知识.思考角度不同,方法就不相同,所涉及的知识也不同,解题的难易程度也不尽相同,对发散学生思维非常重要,它有利于培养学生的创新意识.

(完)