详谈导数处理函数性质难点问题

亢爱锋

(山东省青岛第九中学)

利用导数研究函数单调性是高考数学的重点、热点和难点.因为导数涉及的知识能力和思维层次要求较高,学生运用好导数这个“工具”,对提升学生的分析问题、解决问题、逻辑思维等综合能力都有很大的帮助.其中,利用导数讨论函数单调性的核心是在定义域内判断导函数的正负.而判断导函数的正负,综合考查学生观察分析和综合运用函数、不等式、零点等知识,配方、分离变量和因式分解等数学方法,考查学生对函数与方程、数形结合、等价转化等数学思想掌握情况.高考在这一部分的考查可谓是“芝麻开花节节高”.根据多年对高考题的研究和教学的反思总结,笔者将积累下来的如下解题方法分享给读者.

例1(2015 年全国Ⅱ卷理21,节选)设函数f(x)＝emx＋x2－mx.证明:f(x)在(－∞,0)单调递减,在(0,＋∞)单调递增.

易知f′(x)＝m(emx－1)＋2x.

当x＜0时,2x＜0.

若m＞0,则emx＜1,emx－1＜0,m(emx－1)＜0,故f′(x)＜0,因此f(x)在(－∞,0)上单调递减.

若m＜0,则emx＞1,emx－1＞0,m(emx－1)＜0,从而f′(x)＜0,因此f(x)在(－∞,0)上单调递减.

故当x＜0 时,函数f(x)在(－∞,0)上单调递减.

当x＞0时,2x＞0.

若m＞0,则emx＞1,emx－1＞0,m(emx－1)＞0,故f′(x)＞0,因此f(x)在(0,＋∞)上单调递增.

若m＜0,则emx＜1,emx－1＜0,m(emx－1)＞0,故f′(x)＞0,因此f(x)在(0,＋∞)上单调递增.

故当x＞0时,f(x)在(0,＋∞)上单调递增.

综上,f(x)在(－∞,0)上单调递增,在(0,＋∞)上单调递增.

例2求函数f(x)＝－x＋1的单调区间.

f′(x)＝(x＞0),因此判断函数单调性的关键是判断g(x)＝1－lnx－x2(x＞0)的正负,有以下几种解法.

方法1图像法

观察可知g(x)是由基本初等函数构成的,所以可以将g(x)的正负转化为函数g(x)的零点问题.

令g(x)＝0,移项得1－x2＝lnx,作出函数y＝1－x2,y＝lnx的图像,如图1所示.

图1

由图1可知,当0＜x＜1时,1－x2＞lnx,所以f′(x)＞0,故f(x)在(0,1)上单调递增;当x＞1时,1－x2＜lnx,所以f′(x)＜0,故f(x)在(1,＋∞)上单调递减.

方法2分组正负判断法

因为1－x2,lnx的正负均取决于x与1的大小关系,所以将定义域分为0＜x＜1,x＞1两种情况分类讨论1－x2,lnx的正负.

当0＜x＜1时,1－x2＞0,lnx＜0,所以1－x2－lnx＞0,g(x)＝1－lnx－x2＞0,f′(x)＞0,故f(x)在(0,1)上单调递增.

当x＞1 时,1－x2＜0,lnx＞0,所以1－x2－lnx＜0,g(x)＜0,f′(x)＜0,故f(x)在(1,＋∞)上单调递减.

方法3二次求导法

构造决定导函数f′(x)正负的核心函数g(x)＝1－lnx－x2(x＞0),则g′(x)＝－－2x,显然g′(x)＜0恒成立,故g(x)在(0,＋∞)上单调递减.又g(1)＝0,所以g(x)在(0,＋∞)内有唯一零点为x＝1.故当0＜x＜1时,g(x)＞0;当x＞1时,g(x)＜0.因此,当0＜x＜1时,f′(x)＞0;当x＞1时,f′(x)＜0,于是f(x)在区间(0,1)上单调递增,在(1,＋∞)上单调递减.

例3已知f(x)＝x－lnx,g(x)＝当x∈(0,e]时,比较f(x),g(x)的大小.

比较f(x),g(x)的大小,即判断f(x)－g(x)在x∈(0,e]的正负.令

例4证明:当x＞0时,x2＜ex.

即证f(x)＝x2－ex＜0在x＞0时恒成立.f′(x)＝2x－ex,g(x)＝2x－ex(x＞0),则g′(x)＝2－ex,易知当0＜x＜ln2 时,g′(x)＞0,g(x)单调递增;当x＞ln2时,g′(x)＜0,g(x)单调递减,所以gmax(x)＝g(ln2)＝2ln2－2＜0,所以f′(x)＜0恒成立,故f(x)在(0,＋∞)上单调递减,因此f(x)＜f(0)＝－1,显然f(x)＝x2－ex＜0,从而x2＜ex.

例5已知函数f(x)＝(x＞0).

(1)求函数f(x)在(0,＋∞)上的单调性;

(2)当x＞0时,f(x)＞恒成立,求整数k的最大值.

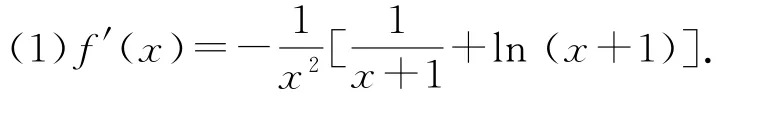
因为x＞0,所以x2＞0,＞0,ln(x＋1)＞0,则f′(x)＜0,所以f(x)在(0,＋∞)上单调递减.

(2)方法1由已知得,当x＝1 时,k＜2(1＋ln2)＜4,因为k∈Z,故kmax＝3,因此只需证当k＝3时,f(x)＞(x＞0)恒成立,即证(x＋1)ln(x＋1)＋1－2x＞0(x＞0)恒成立.

令g(x)＝(x＋1)ln(x＋1)＋1－2x(x＞0),则g′(x)＝ln(x＋1)－1.当x＞e－1 时,g′(x)＞0,g(x)单调递增;当0＜x＜e－1时,g′(x)＜0,g(x)单调递减,从而gmin(x)＝g(e－1)＝3－e＞0,证毕.

方法2即证h(x)＝k(x＞0)恒成立,即hmin(x)＞k.对h(x)求导得

令φ(x)＝x－1－ln(x＋1)(x＞0),则φ′(x)＝＞0,所以φ(x)在(0,＋∞)上单调递增.又φ(2)＝1－ln3＜0,φ(3)＝2－2ln2＞0,所以φ(x)＝0有唯一实根,设为a,则a∈(2,3),a＝1＋lna＋1.

根据单调性可知,当x＞a时,φ(x)＞0,h′(x)＞0,h(x)单调递增.当0＜x＜a时,φ(x)＜0,h′(x)＜0,h(x)单调递减,从而hmin(x)＝h(a)＝＝a＋1∈(3,4),因此正整数k的最大值为3.

例6已知函数f(x)＝(k为常数,e＝2.71828…是自然对数的底数),曲线y＝f(x)在点(1,f(1))处的切线与x轴平行.

(1)求k的值;

(2)求f(x)的单调区间.

(2)由(1)可知f′(x)＝.设g(x)＝－lnx－1,则g′(x)＝－＜0,即g(x)在(0,＋∞)上单调递减.由g(1)＝0 知,当0＜x＜1时,g(x)＞0,从而f′(x)＞0,当x＞1时,g(x)＜0,从而f′(x)＜0.

综上,f(x)的单调递增区间是(0,1),单调递减区间是(1,＋∞).

通过以上例题可以看出,导数法研究函数性质的难点在于如何确定导数的正负,所以解决了导数正负的问题,也就解决了导数的根本.无论是高考题还是平时的模拟训练,通过图像法、逐项或分组判正负法、二次求导(三种不同解决渠道)这三种方法的不断练习,均可以提高学生的逻辑思维能力.

(完)