强基计划校考之复数的备考策略
李桂春
(北京师范大学附属实验中学)
强基计划校考中关于复数内容的考查,除了要求掌握高考中与复数有关的内容:复数的概念(复数的定义、实部、虚部,复数的分类,共轭复数,复数的模,复数的几何意义),复数的代数四则运算之外,还应掌握一些拓展知识,如共轭复数与复数的模的性质、复数的三角形式及运算、实系数的一元n次方程的虚数根的问题,并运用这些知识解决有关问题.
1 必备拓展知识
1.1 共轭复数的性质
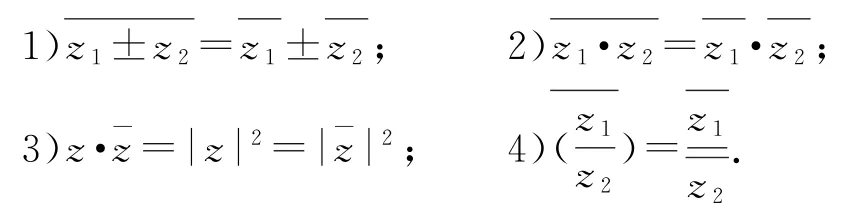
1.2 复数的模的性质

3)‖z1|-|z2‖≤|z1±z2|≤|z1|+|z2|.
1.3 复数的三角形式及其运算
1)复数的三角形式.
设z=a+bi(a,b∈R)对应复平面内的点Z(a,b),连接OZ,记=r,如图1所示,a=rcosθ,b=rsinθ,所以z=r(cosθ+isinθ),这种形式称为复数z=a+bi的三角形式,其中θ称为z的辐角.若0≤θ<2π,则θ称为z的辐角主值,记作θ=argz,r称为z的模,记作|z|,由勾股定理知|z|=
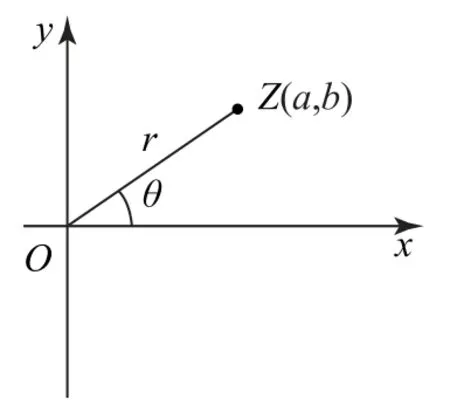
图1
2)复数三角形式的运算法则.
记z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),则

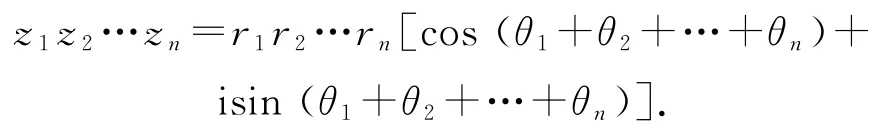
特别地,zn=[r(cosθ+isinθ)]n=rn(cosnθ+isinnθ)(棣莫弗定理).
1.4 常见的运算性质

1.5 有关实系数的方程的复数根
1)复数集内实系数一元二次方程ax2+bx+c=0(a≠0)的解.
当Δ>0时,方程有两个不相等的实数根;
当Δ=0时,方程有两个相等的实数根;
当Δ<0,方程有两个互为共轭的虚数根,即

2)实系数一元n次方程若有虚根,则一定成对出现,并且两两互为共轭复数.
2 复数考查真题分类例析
2.1 考查复数的概念、复数的模及共轭复数的性质
在强基计划校考中,经常考查复数的一些概念,如复数的实部、虚部、模,共轭复数,复数的几何意义等.在解决有关问题时,要充分利用复数的模及共轭复数的性质,有利于简化运算.
例1(2017年北京大学自主招生测试)复数z满足z+为实数,则|z+i|的最小值为_________.


例2(2015年北京大学博雅计划)设z为复数,表示z的共轭,已知且为纯虚数,则|z|的值为_________.

例3(2015年清华大学领军计划,多选)设复数z满足2|z|≤|z-1|,则( ).
A.|z|的最大值为1
B.|z|的最小值为
C.z的虚部的最大值为
D.z的实部的最大值为

设z=x+yi(x,y∈R),则
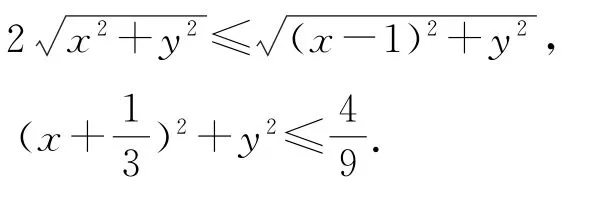
画出复数z所对应的点的图形,如图2所示(圆及其圆内部分),结合图像可知,当复数z对应的点Z为圆与x轴的左侧交点时,|z|取得最大值1,所以A 正确.

图2
当复数z对应的点Z为原点时,|z|取得最小值0,所以B错误.
当x=-时,y取得最大值,所以C正确.
当y=0时,x取得最大值,所以D 正确.
综上,选A,C,D.
例4(2016年清华大学自主招生测试,多选)若复数z满足|z+|=1,则|z|可以取到的值有( ).
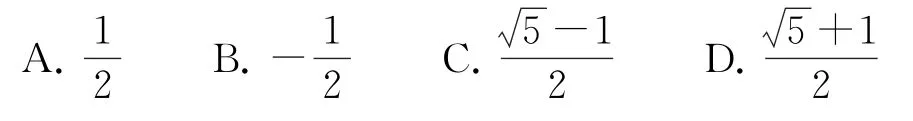

2.2 考查复数的三角形式的运算及性质
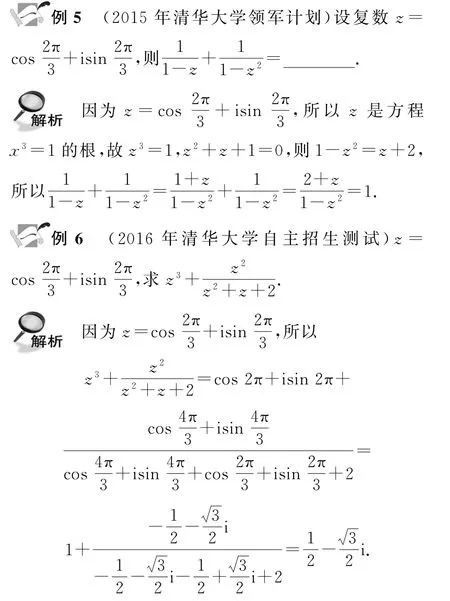
例7(2016年北京大学优秀中学_生暑期学堂测试)复数z1,z2满足|z1+z2|=|z1|,=a(1-i)(a∈R且a≠0),求

设z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),由|z1+z2|=|z1|,得


例8(2016年清华大学自主招生测试)|z2+1|=|z|,求|z|的范围和argz的范围.

设z=r(cosθ+isinθ),其中r>0,θ∈[0,2π),由|z2+1|=|z|,得

所以(r2cos2θ+1)2+(r2sin2θ)2=r2,整理得

2.3 有关实系数的一元n 次方程的虚数根的问题
例9(2016年北京大学博雅计划)设a,b,c为实数,a≠0,c≠0,方程ax2+bx+c=0的两个虚根为z1,z2,且满足是实数,则=( ).
A.1 B.0 C.2 D.以上答案均不正确

例10(2016年北京大学自主招生测试)实系数方程x4+ax3+bx2+cx+d=0有四个非实数根,其中两个之和为2+i,另外两个之积5+6i,求b的值.

实系数方程若存在虚根,则虚根共轭,故设四个虚根为x1,x2,,由题意得x4+ax3+bx2+cx+d=(x-x1)(x-)(x-x2)(x-),则
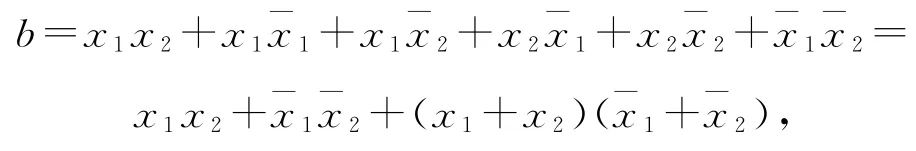
从而b=(5+6i)+(5-6i)+(2+i)(2-i)=15.
2.4 解决有关复数对应点的轨迹问题
例11(2019 年北京大学自主招生测试)复数z1,z2,|z1-3i|=2,|z2-8|=1,则由复数z1-z2围成的面积是( ).
A.4π B.8π
C.10π D.以上答案均不正确

设z1=x1+y1i,z2=x2+y2i,x1,x2,y1,y2∈R,z=z1-z2=x+yi,则

当cos(α-β)=1时,(x+8)2+(y-3)2=1,当cos(α-β)=-1时,(x+8)2+(y-3)2=9,所以复数z1-z2围成的面积为两个半径分别为1和3的圆之间的圆环面积,即S=9π-π=8π,故选B.
例12(2016年清华大学自主招生测试)已知z为非零复数,和的实部与虚部均为不小于1的正数,则在复平面中,z所对应的向量的端点P运动所形成的图形面积为________.

满足上述不等式的区域是如图3 所示的图形中的阴影部分(其中A(10,10),B(10,10),C(10,10),D(20,20)).

图3
该区域由一个四边形ABCD和两个弓形构成.由题意求得,由(a-20)2+b2≤400的半径为20,由余弦定理求得该圆中所对的圆心角为30°,所以以上区域中一个弓形的面积为

四边形ABCD的面积为

所以点P运动所形成的图形的面积为

2.5 利用复数的有关知识解决其他问题
例13(2016 年北京大学自主招生测试)若△ABC的三个顶点对应复数z1,z2,z3,且满足=1+2i,则△ABC的面积与其最长边的平方之比为( ).


如图4 所示,作出△ABC,由=1+2i,得,所以,又

图4

不妨设AC=1,则BC=2,AB=,则△ABC为直角三角形,且AB为斜边,所以S=1,AB2=5,所以,故选C.
例14(2017年北京大学博雅计划)单位圆内接五边形的所有边长与对角线的平方和的最大值是( ).
A.15 B.20
C.25 D.以上答案均不正确

考虑圆内接五边形P1P2P3P4P5,设Pi对应的复数为zi(1≤i≤5),所有线段的平方和为S,注意到有
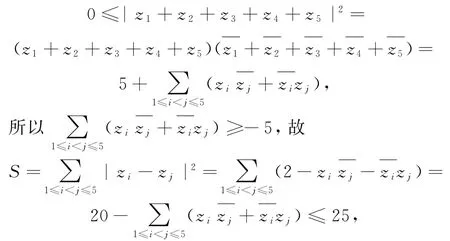
当且仅当|z1+z2+z3+z4+z5|=0,即P1P2P3P4P5是正五边形时,取到等号.故选C.
(完)

