线性模型参数向量的近似贝叶斯估计

蒋 杰,王立春

(北京交通大学 理学院,北京 100044)

§1 引言

考虑如下的正态线性模型

这里y=(y1,y2,...,yn)′表示响应变量,X是秩为p的设计矩阵,β=(β1,β2,...,βp)′为未知参数向量,e是随机误差向量,σ2是未知的误差方差.

在模型(1)中,众所周知β和σ2的最小二乘估计分别为

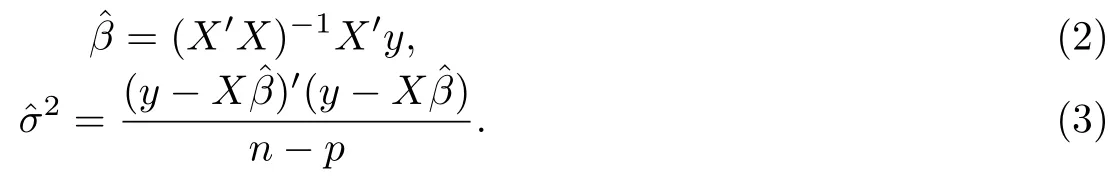
假设π(β,σ2)为β和σ2的联合先验分布,结合似然函数f(y|β,σ2)可得后验分布密度函数h(β,σ2|y).为了获得β和σ2的贝叶斯估计,不妨记作引入如下损失函数

然而,对于这样的多重积分的计算一般无法得到显式解.这促使统计学者们在贝叶斯估计的基础上做了一些研究,来解决多重积分求解困难的问题.比如,文献[1]提出一种近似贝叶斯估计的方法,但是当参数维数超过三时,将涉及高阶导数,这导致计算过程是十分复杂冗长的.另外,MCMC算法也经常是被用来模拟贝叶斯估计的数值解,比如Metropolis-Hastings算法,Gibbs 抽样法等.但通过模拟得到的贝叶斯估计往往只是一个数值解,没有显式表达式,以至于不便从理论上讨论它的统计性质.

近年来利用贝叶斯方法研究线性模型中参数的估计问题,在许多文献[2-4]中多次被提到.对于正态线性模型中参数的贝叶斯估计目前常用的有两种方法,其一,当先验是含有未知超参数的正态分布时,容易知道正态线性模型参数的后验分布依然是正态分布,在平方损失函数下,贝叶斯估计为后验期望,然后利用历史样本估计超参数,得到经验贝叶斯估计的表达式.比如,文献[5]推导了正态线性模型中回归系数的经验贝叶斯估计.文献[6]研究了正态线性回归模型中误差方差的经验贝叶斯估计,并在均方误差(MSE)准则下证明了该估计优于最小二乘估计.第二种为线性贝叶斯方法,其主要思想是通过样本统计量构造待估参数的线性估计,然后再通过最小化贝叶斯风险函数,得到最佳的线性估计即为线性贝叶斯估计,这一方法的优点是不需要知道先验分布具体形式,只需假设先验分布的一些矩是存在的,就能算出线性贝叶斯估计的显式解.在线性模型中线性贝叶斯方法最早由Rao[7]提出,在随后的几十年中受到了很多学者的关注和研究,参见文献[8-11].尤其对于线性模型中参数的估计,文献[12]在假设了先验信息后得到了回归系数的线性贝叶斯估计,并证明了其风险函数以速率O(n−1)在减小.文献[13]在一般的线性模型中推导了回归系数的线性贝叶斯估计,并在均方误差矩阵(MSEM)和Pitman closeness(PC)准则下证明了该估计的优越性.随后,文献[14]研究了分块线性模型中回归系数的可估函数的线性贝叶斯估计.特别地,文献[15]在平衡损失函数下构造了回归系数的线性贝叶斯估计,在MSEM和MSE准则下证明了其优越性,并给出了在PC准则下线性贝叶斯估计优于普通最小二乘估计的充分条件.

通过对这些文献研究内容的分析,鉴于线性贝叶斯估计具有方便使用,并且计算简单等优点.文中试图利用线性贝叶斯方法去近似贝叶斯估计,并得到β和σ2组成的参数向量的线性贝叶斯估计的表达式.本文的主要研究内容是选择合适的统计量去同时构造模型(1)中的回归系数β和误差方差σ2的线性估计.

假设σ2的先验为IG(α,γ),且σ2给定下β的先验分布为N(µ,σ2Σ),于是σ2和β的联合先验密度为

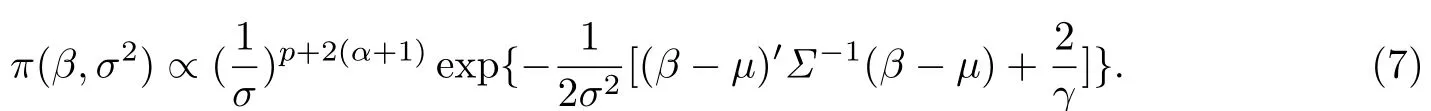
结合似然函数

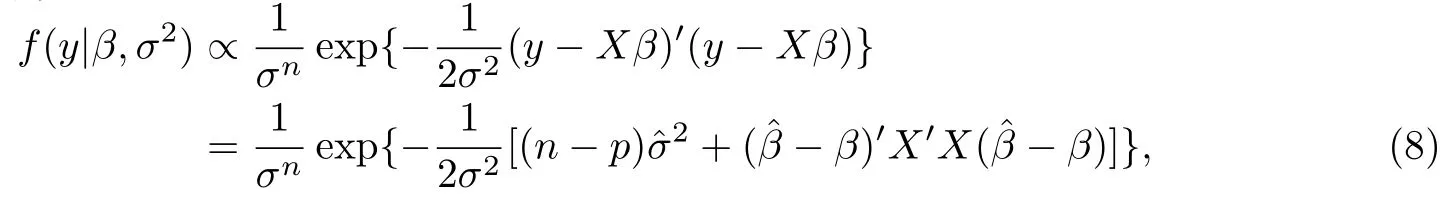
得到联合后验

容易发现联合后验和联合先验有相同的分布形式,于是可以知道

所以σ2的后验期望为

注意到β的边际后验分布为

又因为上式为多元t分布密度函数的核,所以有

§2 构造线性贝叶斯估计

假设参数向量θ=(β′,σ2)′的先验π(θ)属于分布族

这里的E(y,θ)表示y和θ的联合分布期望.

然后利用二次型期望的结果有

证首先计算贝叶斯风险函数

这里利用了如下的事实

和

和

于是有

显然地,从得到的线性贝叶斯估计的表达式以及计算过程可以知道,线性贝叶斯估计不但包含了先验信息,而且避免了求解贝叶斯估计时遇到的多重积分计算较困难的问题.

§3 线性贝叶斯估计的优越性

本节在均方误差阵准则下,证明了线性贝叶斯估计相对于最小二乘估计,其它结构的线性贝叶斯估计以及极大似然估计的优良性.首先计算的均方误差矩阵

这里利用了这样的事实,即FK=F和W=M −

3.1 与最小二乘估计的比较

3.2 与其它结构的线性贝叶斯估计的比较

将W1=FWF′带入(29) 可得

为了证明(31)成立,对矩阵F和M进行分块.令

和

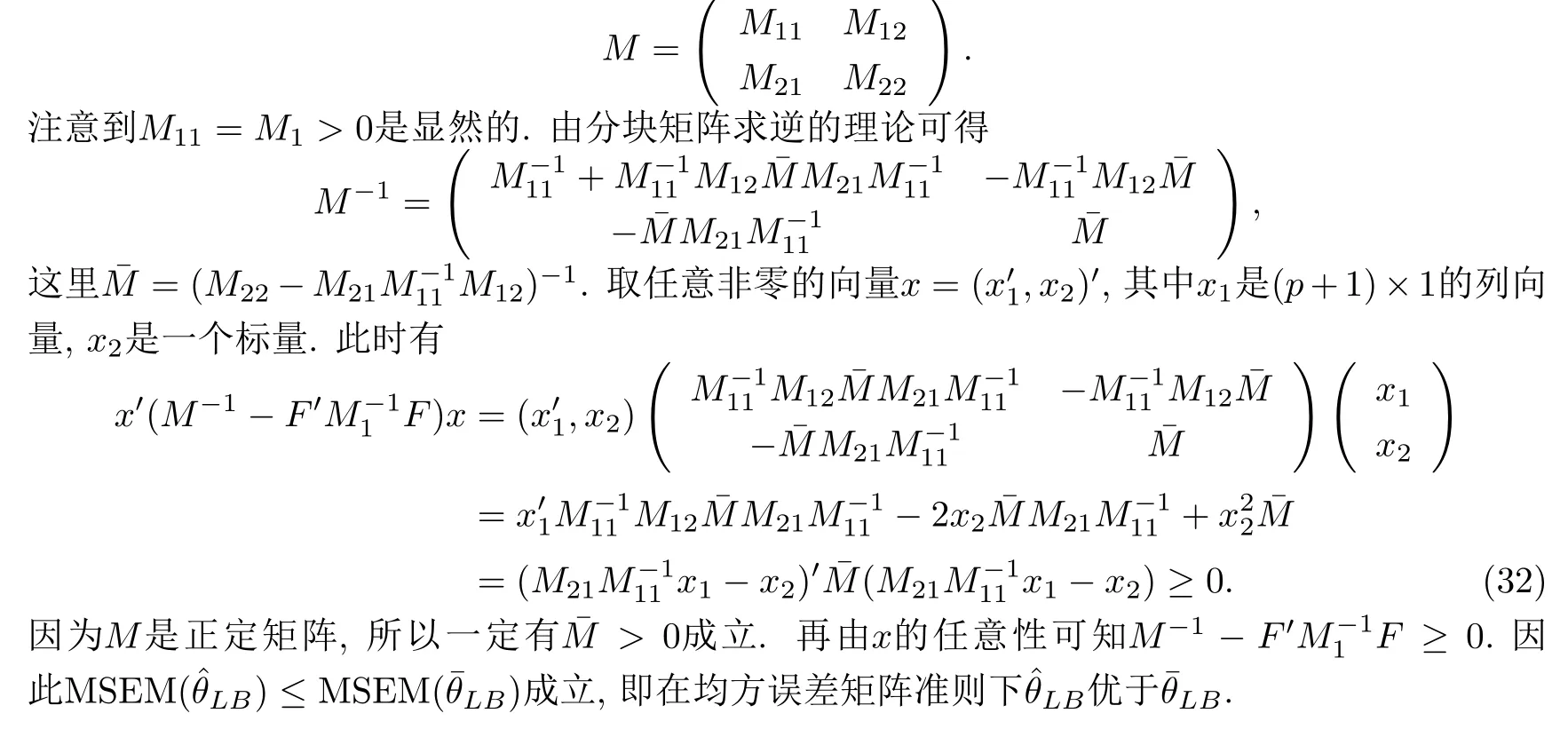
3.3 与极大似然估计的比较

首先计算如下的协方差矩阵以及方差.由二次型期望和方差的相关结论[16],容易知道

所以有

于是可得极大似然估计的均方误差矩阵为

将(36) 和(37) 带入(29),进一步计算得

这是一个2×2的分块矩阵,并且有

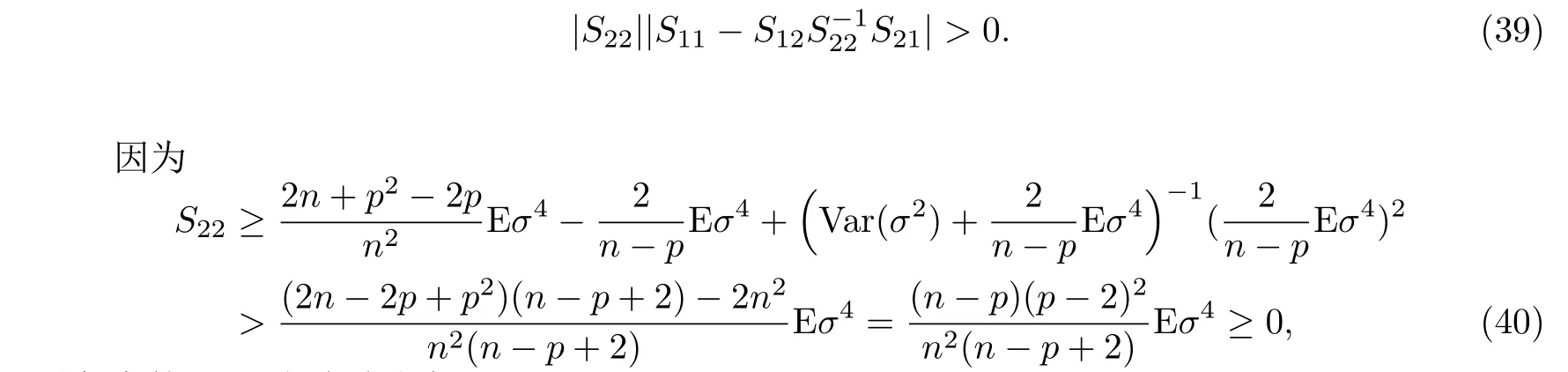
对任意的n>p上式总成立,即S22>0.

§4 数值模拟

在这一节对于几种不同的先验分布,利用MCMC 算法考察了线性贝叶斯估计的数值性质.为了观察对不同的样本大小n的实验效果,取n=20,40,60,80,100,并令p=2,即β=(β1,β2)′.解释变量X中的元素xij,i=1,2,...,n,j=1,2从标准正态分布中采样.系数向量β以及方差σ2的值从先验中取得.y从正态分布N(Xβ,σ2I)中模拟得到.为了获得θ的贝叶斯估计需要假设β和σ2的先验分布.对于先验分布的选择,选取了如下两种不同的先验形式.

情形一假设在σ2给定下β服从正态分布N(µ,σ2Σ),σ2服从均匀分布U(a,b).因此联合后验密度函数为

这里I(a,b)(σ2)表示示性函数.在式子(4) 给出的损失函数下,为y给定下的θ的后验期望的值,此时可以知道通过对式子(5)和(6) 积分求后验期望是无法实现的,所以选择利用Metroplis with Gibbs[17]算法模拟的数值解.首先根据(43) 计算β和σ2的满条件后验分布分别为

这里Σ1=注意,从上式可以知道β的满条件后验分布是均值为µ1,协方差阵为σ2Σ1的多元正态分布,所以可以直接从N(µ1,σ2Σ1)中采样,而σ2的满条件分布不是常见的分布形式,因此,利用Metroplis方法采样,并选取均匀分布作为其建议分布.然后利用Metroplis with Gibbs算法对β和σ2进行采样.具体步骤如下

(1) 给定β和σ2的初始值β(0),σ2(0);用β(j),σ2(j)表示β,σ2在第j步的值,j=0,1,2,···,N;

(2)从N(µ1,σ2(j)Σ1)中产生β(j+1);

(3)用Metroplis方法对σ2进行采样;

(a) 从建议分布中产生候选点σ2∗;

(b) 从均匀分布U(0,1)中产生U;

(c) 判断：若U则接受σ2∗,并令σ2(j+1)=σ2∗,否则令σ2(j+1)=σ2(j).

(4) 重复步骤(2)-(3);

(5) 计算后面N −N0次实验的平均值得到贝叶斯估计.

情形二假设在σ2给定下β服从自由度为v的多元t分布tp(µ,σ2Σ,v),σ2服从卡方分布χ2(t).此时联合后验密度函数为

为了考察θ的线性贝叶斯估计和贝叶斯估计分别与θ的真实值的差异程度,利用了如下欧氏距离公式

在表1给出的四种非共轭先验的情况下,从表2和表3中可以看出,文中选择的统计量T所构造的到真实值的距离,小于由统计量T1所构造的到真实值的距离.这说明更接近θ.这一结论与理论结果也是相一致的.

表1 先验分布的参数取值

表2 在先验Pr1 和Pr2下距离的值

表3 在先验Pr3 和Pr4 下距离的值

并且可以发现对于不同的先验分布,都小于说明当贝叶斯估计无法得到显示解时,利用线性贝叶斯估计去估计真实值,并不逊色于利用Metroplis with Gibbs算法得到的贝叶斯估计.所以从贝叶斯统计角度,除了经典的贝叶斯估计,线性贝叶斯估计同样有不错的性质.另外,还可以发现,当n越大,这些距离都呈现减小的趋势,这表明样本越多获取的信息越多,此时的估计量对待估参数的近似效果越好.

事实上,通过对数似然函数

可以计算出Lijk和信息矩阵的表达式.结果分别如下

表4 先验分布的参数取值

从表5的数值结果以及曲线图1都可以看出,说明更接近于真实值.且随着样本n的增大,两条曲线的差异越来越小.另一方面从的表达式可以知道,当θ的维数增加时,高阶微分的计算复杂度也随之增加,相比之下,线性贝叶斯估计的表达式的获得过程更简单直接.所以由模拟结果和理论研究分析可知线性贝叶斯估计是一种有效的估计.

表5 在先验Pr5和Pr6下,距离‖−θ ‖和‖−θ ‖的值

表5 在先验Pr5和Pr6下,距离‖−θ ‖和‖−θ ‖的值

图1 在Pr5和Pr6 下,距离‖ −θ ‖和‖ −θ ‖随样本的变化情况

另外,为了从数值模拟方面再一次验证用文中提到的统计量T构造线性贝叶斯估计的合理性.在引言中给出的正态逆伽马分布下,对的接近程度进行讨论.表6 给出了先验分布的参数取值.表7 展示了估计量以及距离的值.

表6 先验分布的参数取值

表7 在Pr7下参数估计和距离的值

§5 数值实例

在这一部分利用教育学家测试的21个儿童的智力测试数据[16]，来验证线性贝叶斯估计的有效性.变量y表示某种智力指标,X1为儿童的年龄(以月为单位),数据为y=((95,71,83,91,102,87,93,100,104,94,113,96,83,84,102,100,105,57,121,86,100)′,X1=(15,26,10,9,15,20,18,11,8,20,7,9,10,11,11,10,12,42,17,11,10)′.记X=(1,X1)以及β=(β0,β1)′,这里1是元素全为1的列向量.通过这些数据,建立智力随年龄变化的关系.考虑如下线性回归模型

这里β和σ2是未知参数.对这个模型,主要目的是利用文中提到的线性贝叶斯方法去估计未知参数β和σ2.在表8给出的两种先验下,分别计算了的距离.

表8 β和σ2的先验分布

从表9可以看出,与其它几种估计相比,线性贝叶斯估计与贝叶斯估计非常接近,而Lindley近似作为贝叶斯估计的另一种近似估计,在这里表现得相对比较糟糕,并且表达式也很繁琐复杂.因此,可以说线性贝叶斯估计是一种合理可行的估计.

表9 不同先验分布下的距离

§6 结论

本文在正态线性模型中,利用线性贝叶斯方法同时估计了其回归系数β和误差方差σ2,并在只假设先验的某些矩存在而不知道先验的具体形式的情况下,得到了参数向量θ=(β′,σ2)′的线性贝叶斯估计的表达式.然后在均方误差矩阵准则下,证明了线性贝叶斯估计优于经典的最小二乘估计和极大似然估计.从数值模拟方面,选取了四种不同的先验分布,利用Metroplis with Gibbs 算法模拟得到θ的贝叶斯估计并且从数值模拟的结果中可以看出更接近参数真值.作为对比,引入Lindley 近似通过分析发现有一个更好的近似表现.因此,从模拟的角度再次验证了线性贝叶斯估计的优越性.更重要的是,在参数向量高维情况下,Lindley 近似的表达式涉及高阶微分的计算,且计算过程随着待估参数维数的增大也越来越复杂,此时想要获得Lindley 近似的表达式是非常困难的,然而,维数的增大对于线性贝叶斯估计的表达式的获得并没有影响.所以待估参数维度增大时,相对而言,线性贝叶斯估计计算更容易,表达式也更简洁.最后,用一个数值实例验证了线性