含定性因子的二阶Scheffé模型多目标最优设计

凌 羚,李光辉,张崇岐

(1.广州大学 经济与统计学院,广东广州 510006;2.凯里学院 理学院,贵州凯里 556011)

§1 引言

混料试验在众多领域都有着广泛的应用.2011年Cornell[1]将混料模型应用于雏鸡饲养及水果饮料配方研发.2019年,Goos和Hamidouche[2]将混料应用于鸡尾酒实验,Zijlstra等[3]通过混料模型来描述流动性预算的偏好和偏好异质性.近年来,对于混料模型的最优设计研究,一般都集中于D-,A-,I-等单目标最优准则.例如,李光辉等[4]研究了具有复杂约束混料试验的渐近D-最优设计;刘妙玲等[5]研究了一阶半变系数混料模型的D-最优设计;朱小渊等[6]研究了缺失项二阶混料模型的I-最优设计.

现在随着试验成本的不断上升,研究人员使用传统的单目标试验优化方法去处理多个目标时,不仅会额外增加试验次数,还会浪费大量的人力,物力资源和时间成本.例如,考虑某一混料模型的D-与A-最优性.D-最优设计在使参数向量的置信椭球体积达到最小时,往往会存在某些参数估计值的方差较大;而A-最优设计在使得模型中未知参数最小二乘估计的方差之和达到最小时,又会令置信椭球体的体积变大.因此,本文的目标是找到一种高效的多目标优化设计,既能平衡各种目标的效率,又能为更重要的目标提供更高的效率.

众多学者提出了各种不同的方法研究多目标优化试验问题.1971年,Stigler[7]在研究多项式回归模型最优试验设计时,提出了C-约束D-最优设计.该设计在考虑单最优准则对参数估计的约束效果同时,仍然允许对模型进行检验.1983 年,Mikulecka[8]利用凸优化技术研究了C-约束D-最优性,基于惩罚方法导出了C-约束D-最优设计的数值算法.1988年,Lee[9]基于Fréchet导数给出了一个约束最优设计的充要条件.1990年,Dette[10]提出了适用于多项式回归模型的组合优化设计.1994年,Cook和Wong[11]证明了在一定条件下,约束最优设计和组合最优设计这两种寻求多目标优化设计的方法是等价的.1998年,Huang和Wong[12]提出了一种基于序贯方法构造非线性模型的多目标局部最优设计.2008年,Atkinson[13]给出了在模型识别和参数估计之间提供特定平衡的DT-优化设计.这些研究大部分都是基于两目标组合优化设计.2015年,Hyun和Wong[14]构建了一种基于logistic模型的三目标优化设计,并对每一个目标给定了用户感兴趣的效率.以上文献几乎都是研究的多项式回归模型多目标优化设计,并不适用于混料模型.2012年,Zhang[15]等提出了混料模型的多目标优化设计,该文基于两分量二阶混料规范多项式模型,通过图检验法,导出了两目标约束最优设计.

本文由四个部分组成.§1为引言;§2介绍了含定性因子的混料模型和两种常见的多目标优化设计方法;§3基于q分量s水平混料分类模型,通过对研究者感兴趣的目标设置相应的权重,导出了模型的多目标优化设计,并由方差函数证明了组合设计的最优性;§4给出结论并对多目标优化设计未来的研究进行了展望.

§2 模型与最优准则

2.1 含定性因子的Scheffé模型

混料试验设计通常假设响应变量y仅与试验中各分量比例x1,x2,···,xq有关,而与总量无关.由各分量比例所确定的q −1维试验域可表示为

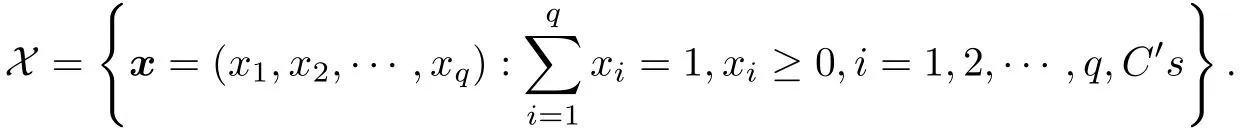
其中C′s为附加约束条件.当模型不含附加约束时,称之为q −1维正规单纯形,记作Sq−1.在混料设计中使用较多的是Scheffé中心多项式模型

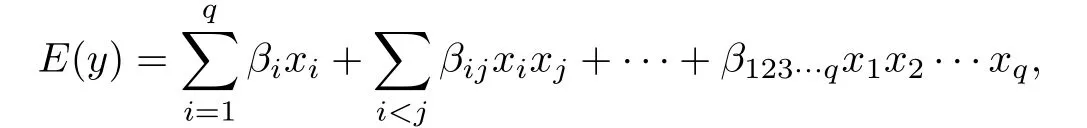
其特点是在不降低模型阶数,保持预测精度的条件下减少了试验次数.

但在许多实际问题中,响应不仅仅受到各混料分量的影响,还会受到其他变量的影响.这类模型可表示为

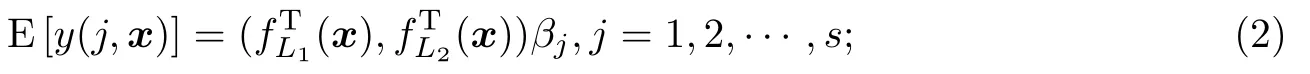
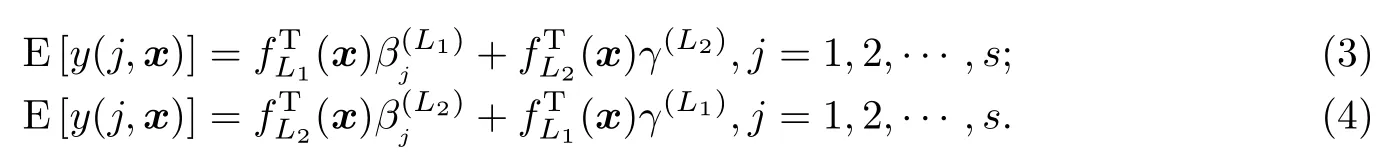
其中模型(2)一次项与交互项部分都受到定性因子影响;模型(3)的一次项与交互项部分分别为因子效应及固定效应;模型(4)的一次项与交互项部分分别为固定效应及因子效应.例如,某医师希望对治疗新冠肺炎的两种不同的药物-连花清瘟颗粒和清肺排毒汤的疗效进行比较,两种药物的药效对患者性别之间的差异可视为模型(3),(4)中的第一部分,药物的固定药效可视为两模型的第二部分.

2.2 最优设计

一个k点设计可表示为

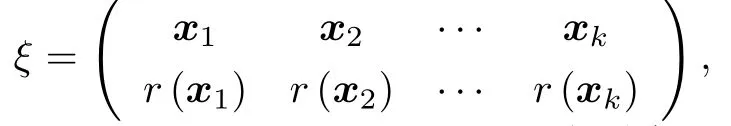
其中x={x1,x2,···,xk},r={r(x1),r(x2),···,r(xk)}分别表示设计ξ的试验点集与各点对应的测度,且=1.令所有设计的全集Ξ为一个设计空间,最优设计就是确定一个设计ξ ∈Ξ,使得该设计信息矩阵M(ξ)在某种意义下达到最优.D-最优与A-最优设计在应用领域非常普遍.D-最优设计是将信息矩阵的行列式最大化,从而使得参数向量的置信椭球体积最小.即

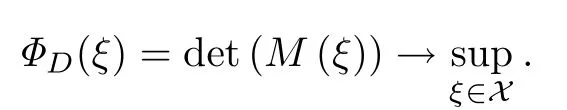
一个设计ξ是D-最优设计的充分必要条件是

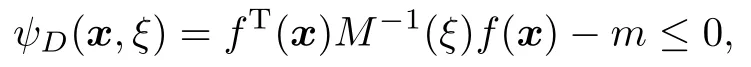
其中m是模型中未知参数向量β的维数,ψD(x,ξ)是设计ξ在D-准则下的方差函数,当ψD(x,ξ)在柱点处等于0时,则设计ξ是D-最优设计.

A-最优设计是将信息矩阵逆的迹极小化,从而使模型未知参数最小二乘估计的方差之和达到最小,即

若一个设计ξ是A-最优的,则有

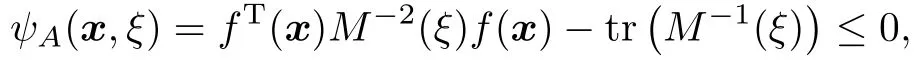
且ψA(x,ξ)在柱点处等于0.

约束最优设计与组合最优设计是研究者常用的两种求解多目标最优设计的方法.约束最优设计一般假设试验必须满足两个截然不同的目标φ1和φ2,它们分别表示在信息矩阵上定义的主要和次要目标.为了平衡这些相互竞争的目标,可以选择一个主要目标效率不低于某一常数时,次要目标效率尽可能高的设计[7].令∆c表示存在常数约束c的约束最优设计集,当设计ξ受限于φ1(ξ)≥c时,有

容易证明∆c是一个凸集.此时最优设计ξc应该满足ξc=arg max∆c φ1(ξ).

组合最优设计是基于两目标函数φ1和φ2的加权平均[10],可表示为

其中0≤λ ≤1.最开始研究者试图通过选择一个恰当的权重λ,来反映两个不同目标的相对重要性,但实际表明,λ值的选取与设计的效率之间没有明显的联系.例如,当λ=0.5时,并不能表明研究者对两目标的兴趣是一致的.

§3 主要结果

3.1 两目标最优混料分类试验设计

基于q分量s水平二阶混料分类模型,研究者感兴趣的目标分别为模型的D-最优与A-最优性.D-最优设计可以使信息矩阵的行列式达到最大,从而使模型中未知参数估计建立的置信椭球体体积达到最小.但在构造模型的D-最优设计时,会存在少数参数估计值的方差较大,因此第二个目标考虑它的A-最优设计,希望模型中未知参数估计的诸分量方差之和尽可能的小.

以Ds={1,2,···,s}表示定性因子的s个处理,记z=(j,x)∈Ω,Ω=Ds ×X为混料试验域与定性因子构成的直积试验域.则试验域Ω上的设计可以表示为两部分设计的直积形式,即ζ(j,x)=η(j)×ξ(x),这里η是试验域Ds上的设计,ξ(x)是试验域X上的设计.则ζ具有如下形式

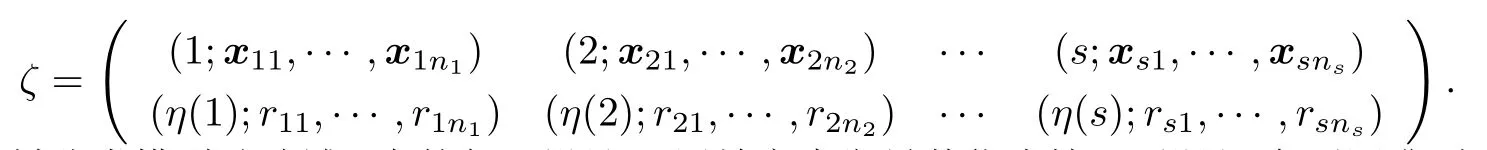
对于混料分类模型试验域Ω中的任一设计ζ,用效率来衡量其优劣情况,设计ζ在不同准则下的效率分别为

其中,detM(ζD)为D-最优设计信息矩阵的行列式,trM−1(ζA)为A-最优设计信息矩阵逆的迹,eD(ζ)和eA(ζ)分别为某一设计ζ的D-效率和A-效率.如同2.2节叙述的约束最优准则,研究者希望当主要目标效率较高时,次要目标效率尽可能的高.因此本文的主要目的是使两目标效率和达到最大

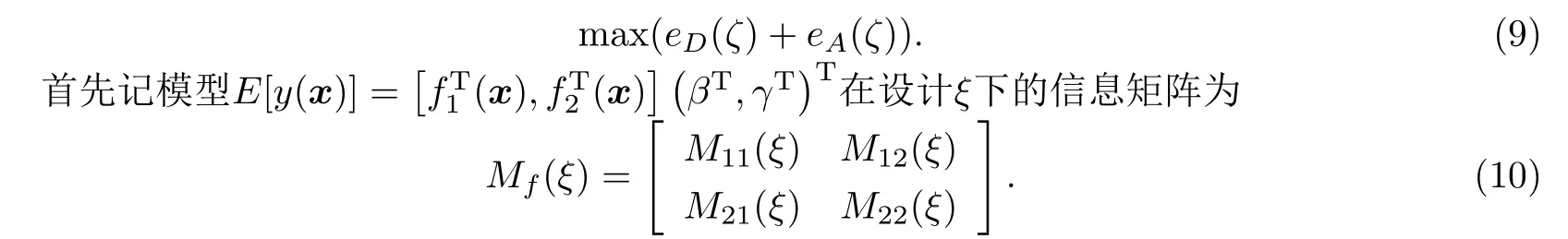
把模型(1)写成矩阵乘积形式

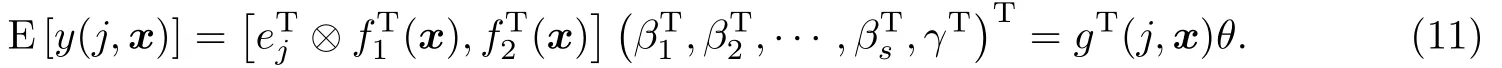
可得出模型(11)在设计ζ下的信息矩阵为

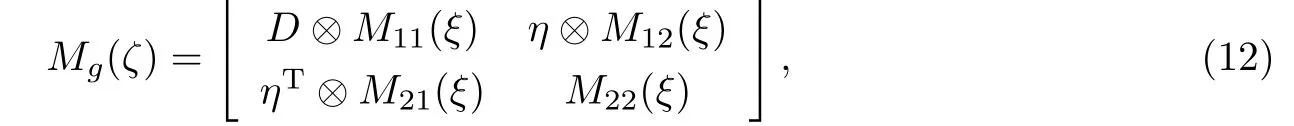
其中D=diag{η(1),η(2),···,η(s)},η=[η(1),η(2),···,η(s)]T.信息矩阵行列式为

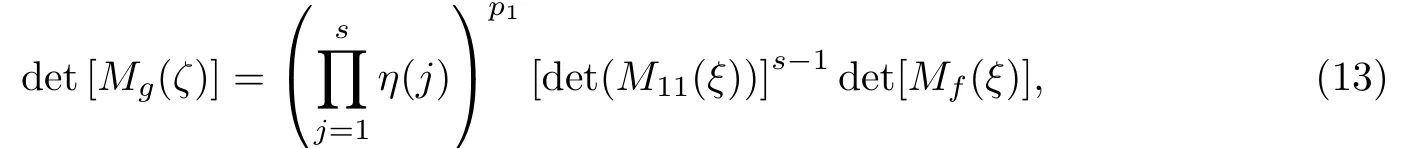
信息矩阵的逆的迹为

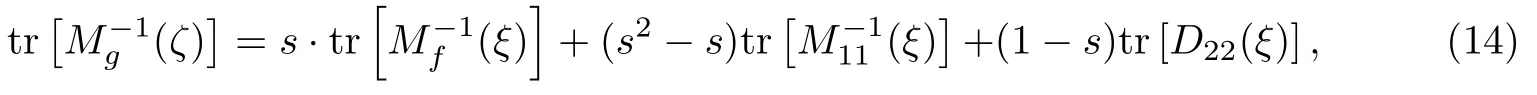
其中D22(ξ)=

对于模型(3),混料区域上的设计ξ使用二阶广义中心设计点集C{q,2}来安排试验,=(x1,x2,···,xq)T与=(x1x2,x1x3,···,xq−1xq)T分别为二阶中心多项式的一次项与交互项函数向量.定性因子部分取其试验域Ds上的均匀设计,记

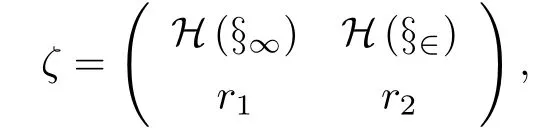
这里x1=(1,0,···,0)T,x2=(1/2,1/2,···,0)T分别是单纯形上的顶点和棱中点,H(xi)={xi1,xi2,···,xini}是xi,i=1,2的置换点集,所对应的各点测度满足n1r1+n2r2=1.以

分别表示方差函数在两类设计点处的值.若设计ζ是D-最优的,一方面应有

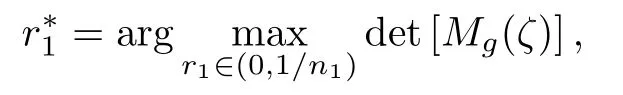
另一方面应有

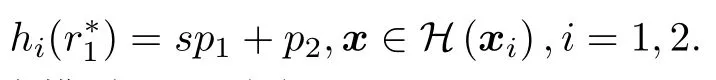
对于3分量4水平二阶混料分类模型,可以求得

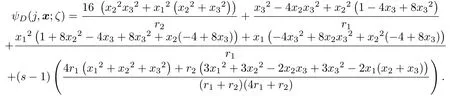
令函数

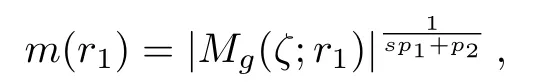
随着r1∈(0,1/n1)的变换,m(r1)的变化过程如图1(左)所示,可知模型的D-最优测度为r1=0.2354,行列式值为0.042.图1(右)显示了h1(r1)与h2(r1)的变化过程,可见当r1=时,h1(r1)与h2(r1)交于一点,该点坐标为=(0.2354,15).

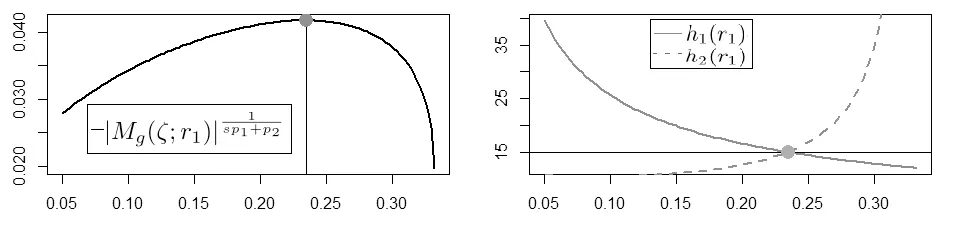
图1 3分量4水平二阶混料分类模型D-最优设计结果

由(7)式可得设计ζ的D-效率为

同理模型在A-最优准则下的方差函数为

易知当r1=0.1838时,该设计的D-,A-效率和最大,值为1.962.此时每个目标效率如下

由下面不等式可确定权重α,使得该设计满足对应的组合最优性条件

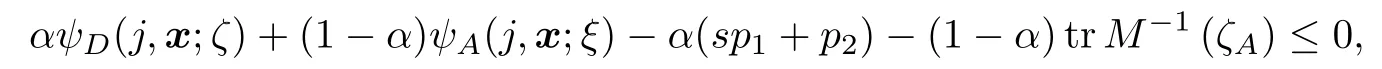
其中α ∈[0,1],且当x为柱点时等号成立.表1和图2给出了不同权重下D-,A-两准则组合最优设计相应效率及效率和.由图2可以看出,随着α值的增大,设计ζ∗在D-最优准则下的效率不断上升,在A-最优准则下的效率不断下降.由表1可知,当设计ζ为D-最优或A-最优设计时,它的效率和都无法达到最大.当α=0.99时,效率和最大.此时每个目标效率如下:

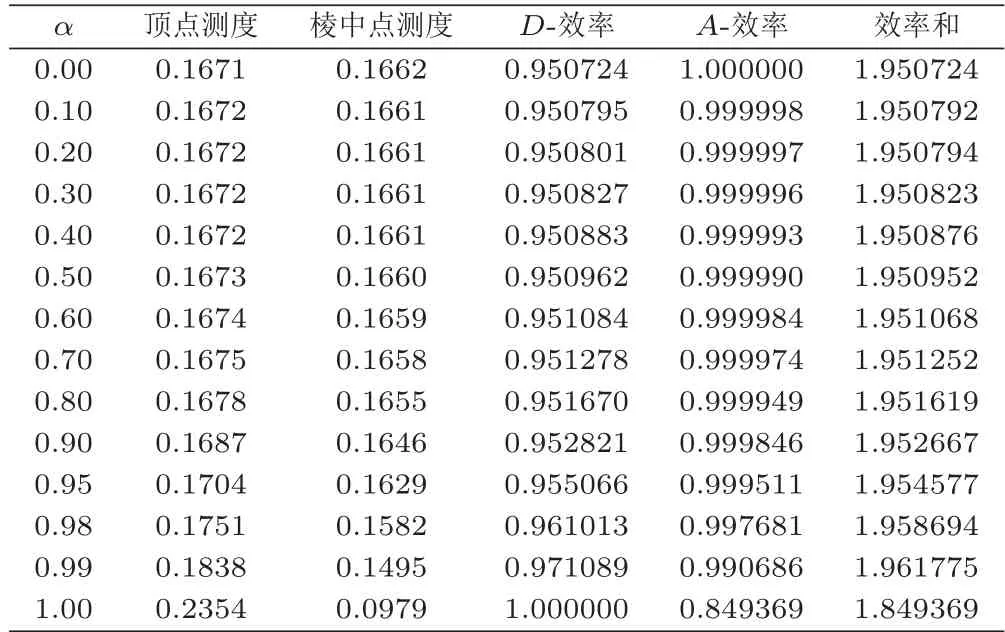
表1 D-, A-两准则组合最优设计及其效率和

图2 组合最优设计效率

直接通过求解效率和达到最大时的测度,然后再解出相应测度满足组合最优性时的权重值,得到新的组合最优设计ζ∗.与以往的方法相比,仅需一步求最值,少了大量迭代过程,计算更为简便,结果更加精确.

3.2 多目标最优混料试验设计

上节讨论了q分量s水平混料分类模型的两目标最优设计,而对于混料可加模型,Becker模型等其它混料模型的多目标最优设计,该方法同样适用.众所周知单纯形-中心设计具有在不降低模型阶数且保持预测精度的条件下减少了试验次数的优点,因此基于二分量二阶混料中心多项式模型,作者感兴趣的三个目标分别为模型的R-最优,D-最优与A-最优性.

设计ξ是R-最优设计[16]当且仅当方差函数ψR(x,ξ)满足条件

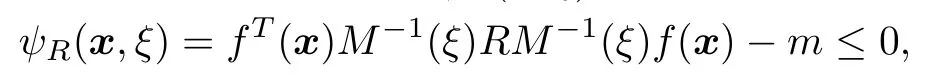
且ψR(x,ξ)在柱点处等于0.其中R=diag{1/M11,1/M22,...,1/Mmm},Mii,i=1,2,...,m是M−1(ξ)中主对角线上的元素.

众所周知对于二分量二阶混料中心多项式模型,它的R-最优设计的试验点在单纯形的顶点和棱中点上,且易算出测度为r1=0.375.设计ξ的信息矩阵为

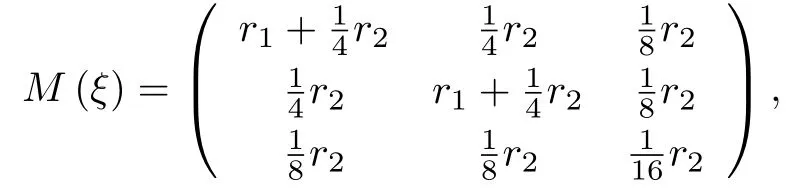
相关矩阵为

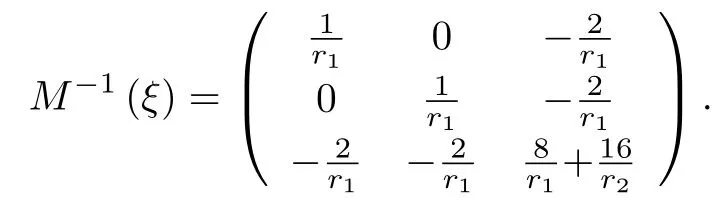
由式(7),(8)可知设计ξ的A-效率,D-效率和R-效率分别为

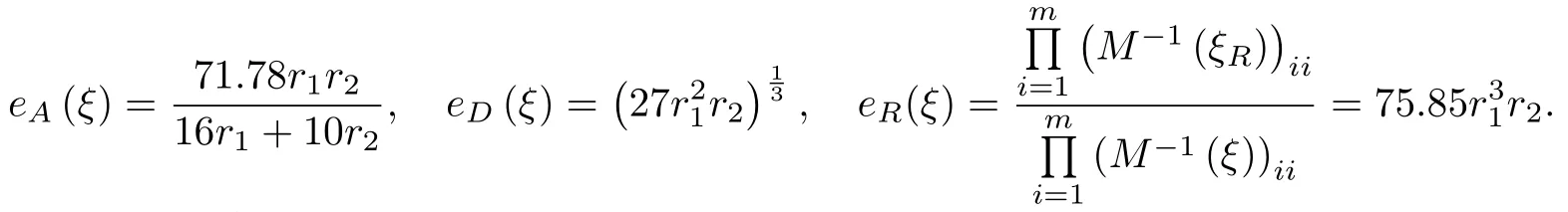
进而最大化这三个最优准则的效率和可写为

进一步求得r1=0.30,r2=0.40.此时三目标效率和达到最大,值为2.79.再通过下面不等式可确定每个感兴趣目标的相应权重,使得设计ξ∗满足组合最优性条件

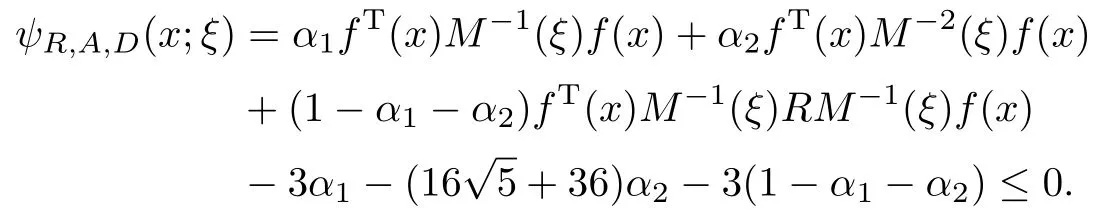
以往求解3个或更多目标优化设计问题时,一般先考虑任意两个目标确定双目标优化设计,然后依次配对其余的目标,最终确定多目标优化设计.然而该方法计算复杂,还会出现一定误差.本文提出的方法仅需求得多个目标效率和最大时的测度,计算简单,且可以得到精确的结果.

§4 进一步讨论与总结

多目标最优设计的提出,改进了传统单目标最优设计在实际应用中的不足.本文研究了q分量s水平混料分类模型的多目标最优设计问题,通过求解不同准则下效率和取极值时的测度,得到新的多目标最优设计ξ∗,并证明了该设计满足相应组合最优性.实例证明,该方法同样适用于求解3个或更多目标优化设计问题,且计算更为简便,结果更加精确.在之后的研究中,可以考虑如何寻找不同用户指定效率的稳健多目标优化设计,并证明该设计是否满足相应最优性.