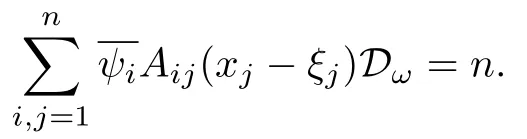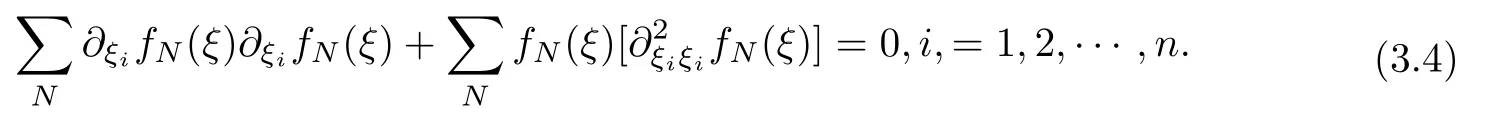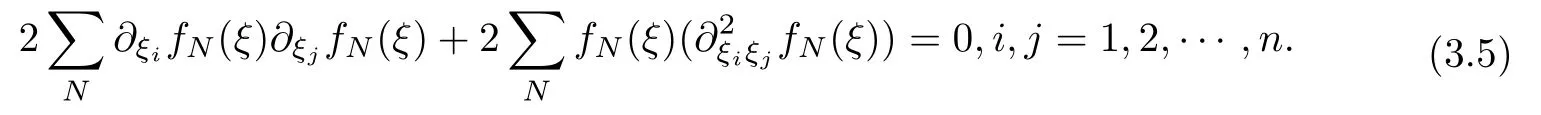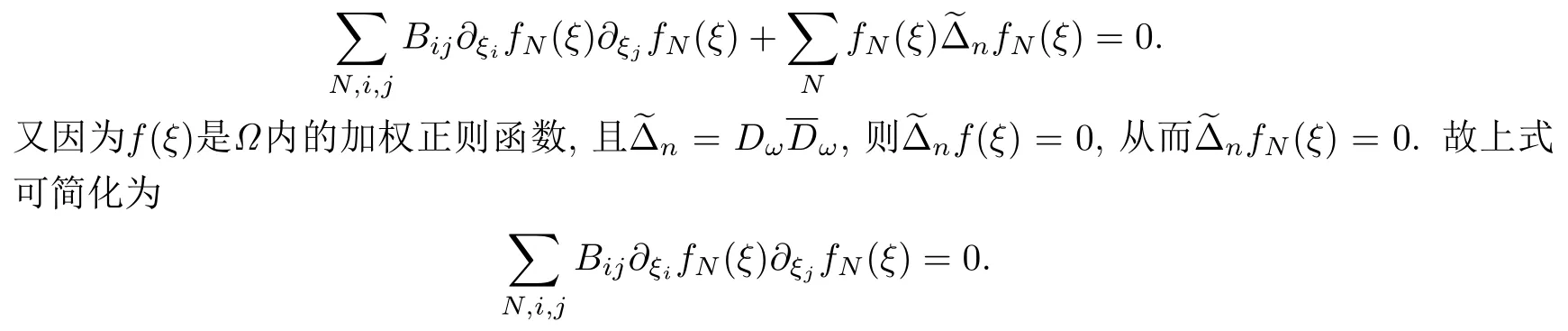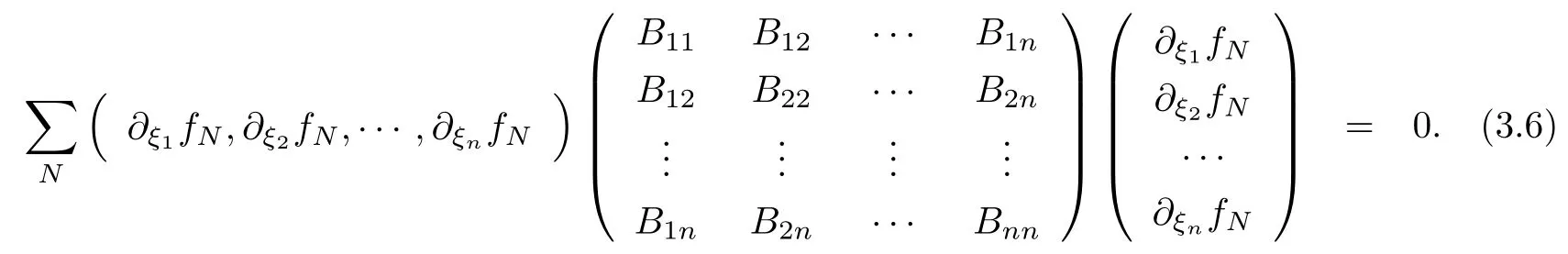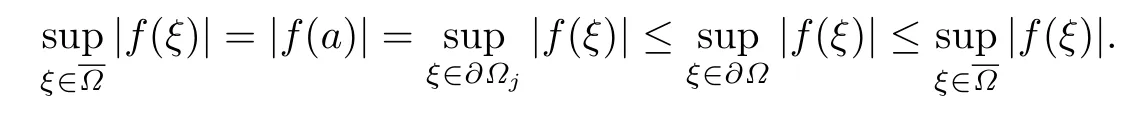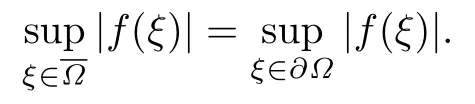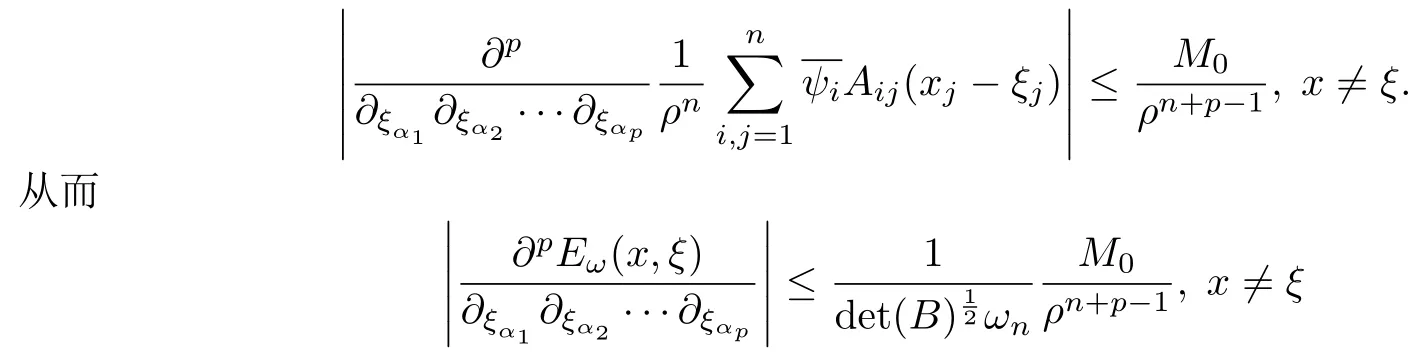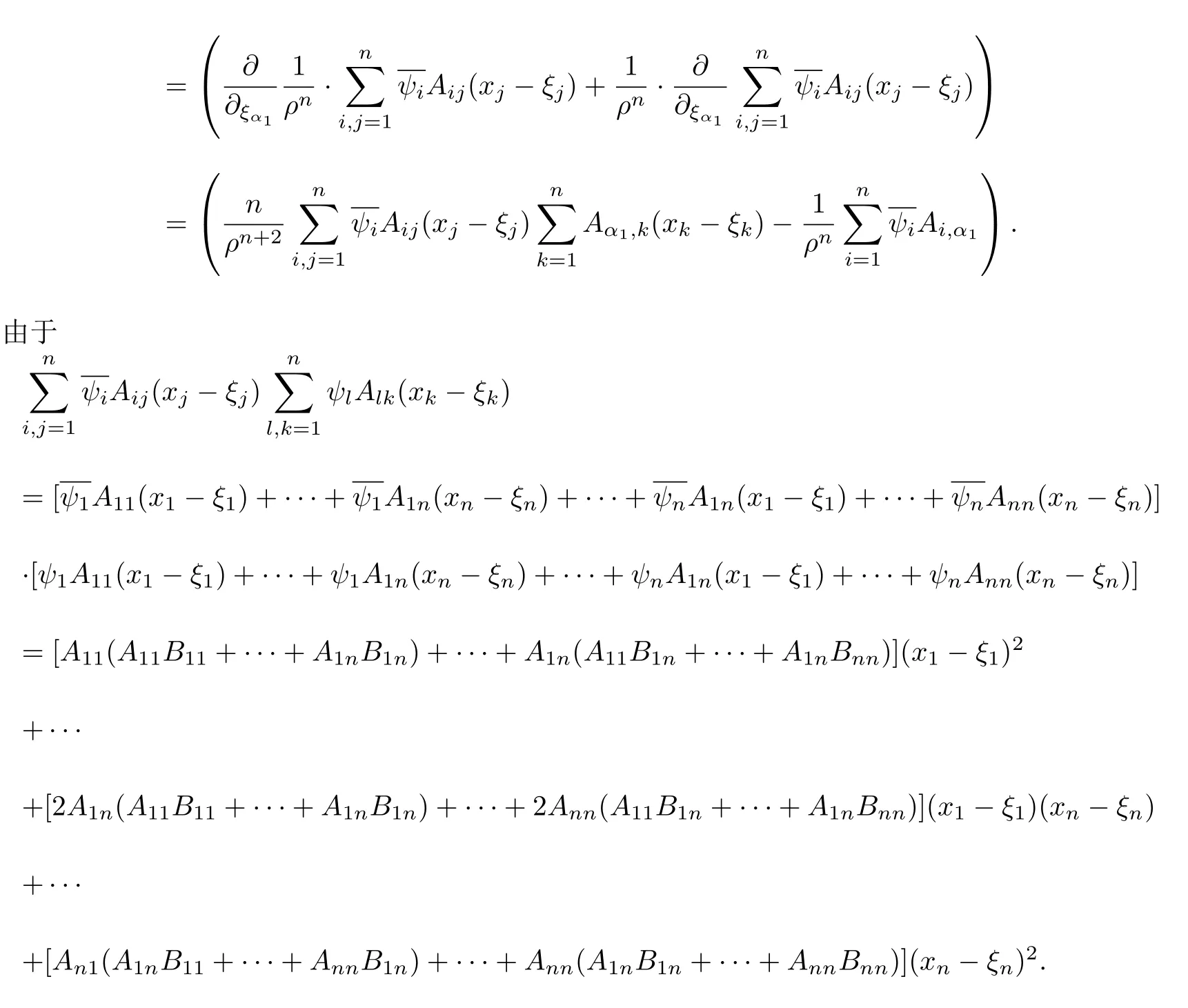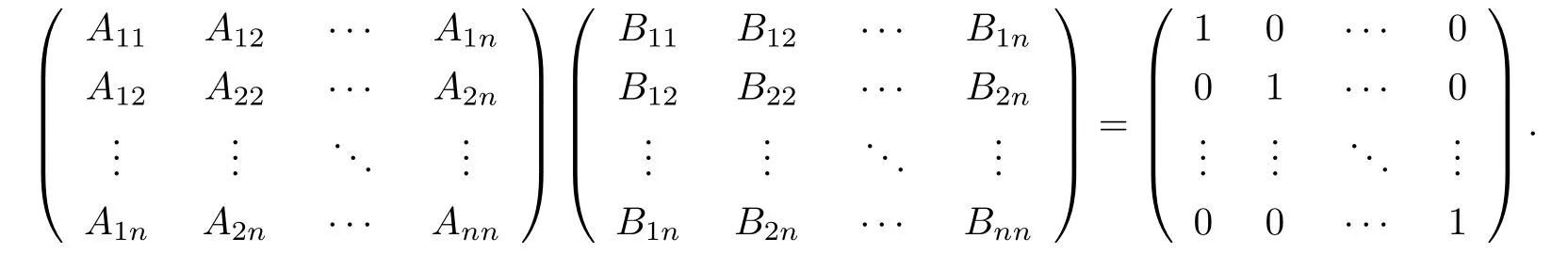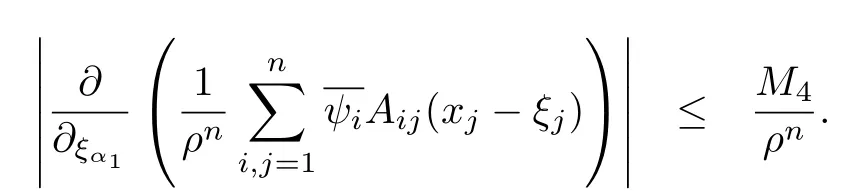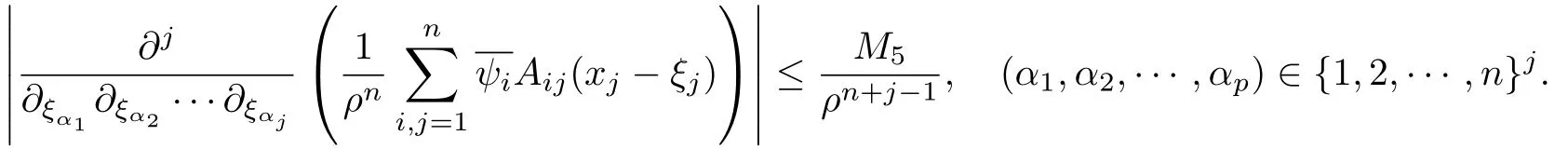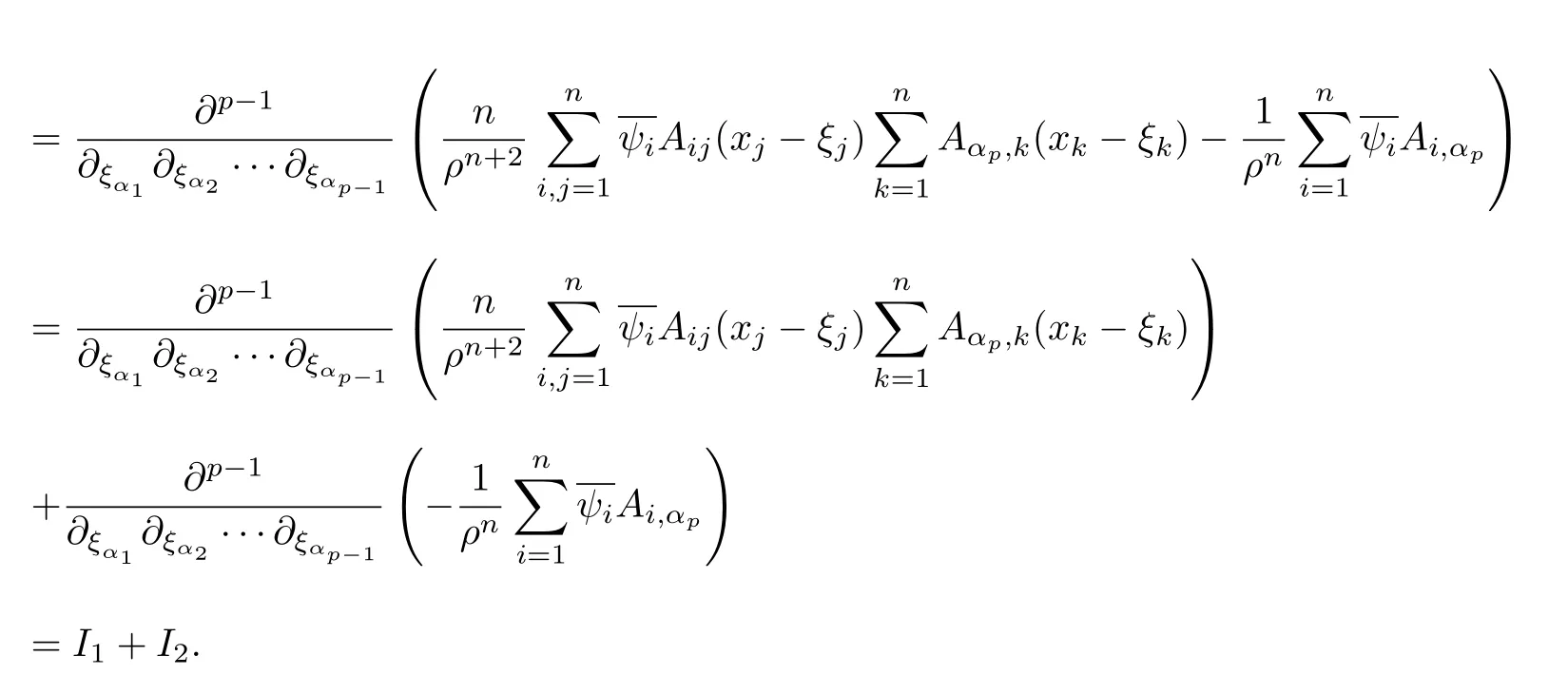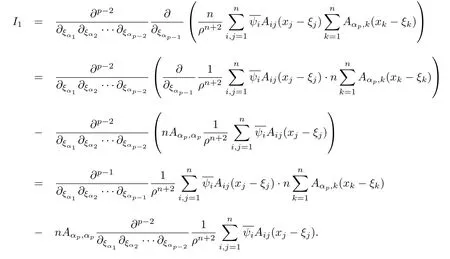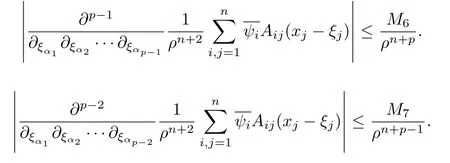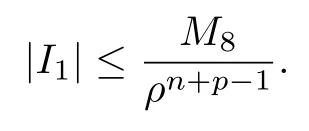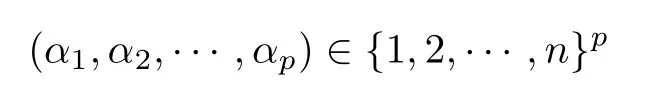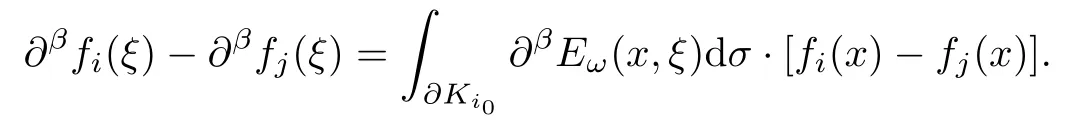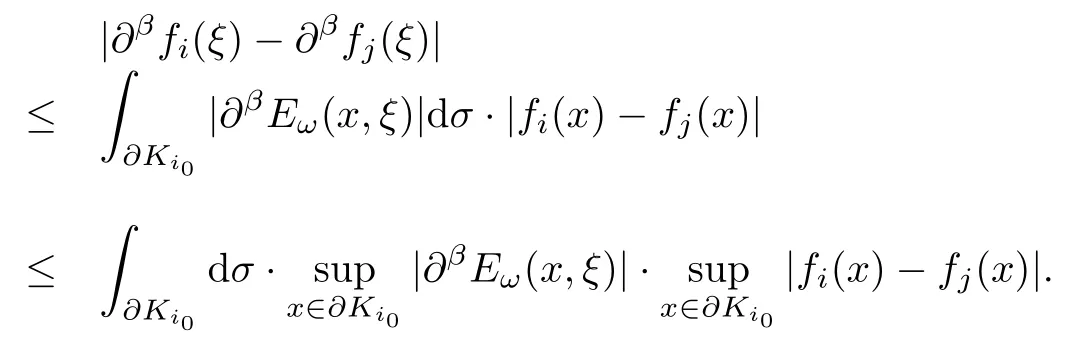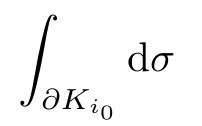加权正则函数的一些性质
罗利萍,王丽萍,邱 芬
(河北师范大学 数学科学学院,河北石家庄 050024)
§1 引言
Clifford代数是复数,四元数,外代数的推广.Clifford分析是关于Dirac算子零解的函数理论,Dirac算子是著名的Cauchy-Riemann算子在高维情形下的发展.Dirac算子特殊的结构使它成为联系偏微分方程,微分几何以及物理学的重要桥梁,这也使得对Dirac算子的研究具有很重要的意义.1968年,D.Hestenes引入了Dirac算子,并且研究了Dirac算子在Clifford分析中的重要作用,证明了实Clifford分析中的Morera定理及Liouville定理[1].直到1982年,F.Brackx,R.Delanghe,F.Sommen等给出了正则函数的Cauchy-Riemann方程,Cauchy-Pompeiu公式,Cauchy积分公式,Sokhotski-Plemelj公式,平均值定理,最大模原理,Weierstrass定理等许多结果[2],从而将单复分析中全纯函数在高维空间欧氏度量下进行了推广.随后,国内外许多学者开始致力于Clifford分析的研究.在国外,K.G¨urlebeck,W.Sprssig,U.K¨ahler,H.Begehr等都对Clifford分析做过大量的研究[3-6].在国内,杜金元[7],黄沙和乔玉英[8]等较早开始研究Clifford分析,并取得了一系列较好的研究成果.近几年,乔玉英和王丽萍等又研究了Clifford分析中一些高阶奇异积分算子的性质及有关偏微分方程边值问题,得到了很好的结果[9-12].然而,为了能更好地描述物体的特征,经典Dirac算子已经不能满足要求,譬如各向同性介质中的热传导问题,可以在经典Clifford代数结构上利用经典的Dirac算子进行描述.但对于涉及到非均匀材料的物理问题,譬如各向异性介质中的热传导问题,经典的Dirac算子就不能很好地对这类问题进行描述,就需要在依赖于参数的Clifford代数结构上利用加权Dirac算子进行描述.因此,2012年,A.N.Di.Teodoro,C.J.Vanegas在含参量Clifford代数下给出了一阶meta-monogenic算子的基本解及Cauchy-Pompeiu公式[13].2013 年,C.Balderrama,A.D.Teodoro,A.Infante在含参量Clifford代数下给出了n阶meta-monogenic算子的Cauchy-Pompeiu公式及应用[14].2016年,A.G.Eusebio,A.D.Teodoro研究了第一类multi-meta-weighted-monogenic函数的Cauchy-Pompeiu公式,并给出了非齐次meta-n-weighted-monogenic方程的分布解[15].2017年,A.G.Eusebio,A.D.Teodoro又研究了第二类multi-meta-ϕ-monogenic函数的积分公式[16].2018年,J.Vanegas,F.Vargas研究了带有Clifford常数权γi ∈An(R)(i=1,2,···,n) 的Dirac算子Dω=的基本解,其中Dω是二阶椭圆微分算子的因子,B=(Bij)是对称的正定矩阵.随后,J.Vanegas,F.Vargas又给出了该类加权正则函数的Borel-Pompeiu公式与Cauchy-积分公式[17].当函数f满足方程Dωf=0时,则称其为加权正则函数.加权正则函数是Clifford分析中的一类重要的函数,是正则函数的推广,当矩阵B是单位矩阵的时候,加权正则函数是正则函数.
本文研究加权正则函数的一些性质,文章的结构安排如下:§2回顾了有关Clifford分析的一些基本知识,加权Dirac算子的定义以及与加权Dirac算子有关的积分公式.§3研究了加权正则函数的平均值定理,最大模原理,Weierstrass定理以及一些推论.这些性质刻画了实Clifford分析中加权正则函数的基本特征.
§2 预备知识
设{e1,e2,...,en}是n维欧式空间Rn的一组标准正交基,An(R)是建立在Rn上的2n维实Cli-fford空间,且基底表示为β={eN|N ∈Γn},其中Γn={0,1,2,···,n,12,13,···,123···n},e0为其单位元,An(R)中的基元素可表示为:其中1≤N1<··· 定义a的模为 设Ω ⊂Rn是一个有界域且边界∂Ω充分光滑,接下来考虑定义在Ω取值于An(R)中的函数f,则f可表示为其中fN(x)是定义于Ω上的实值函数.用表示Ω中r阶导数连续的函数的全体, 加权Dirac算子定义为 便于计算,将Dω表示为 其中ψi=γiei,i=1,2,···,n. 或 当ψi=ei时,则(2.4),(2.5)变为 其中矩阵B为单位矩阵,加权Dirac算子Dω退化为经典Dirac算子D= 基于正定矩阵的不同分解,例如Cholesky分解B=LLT(L是下三角矩阵,且对角线上元素Lii >0,i=1,2,···,n),平方根分解L′=以及根据奇异值分解B=UΛUT得到L′′=来构造加权ψi.如果定义ψi是矩阵L的第i行嵌入到了Rn的标准基中,即 经计算,满足 另一个公式也可通过计算得到. 根据(2.6)所构造的加权ψi是向量值函数,也可以构造不是向量值的加权ψi. 利用引理2.1中的(2),有 之后只考虑(2.8)给定的加权ψi的形式. 定义2.1设f ∈若对任意x ∈Ω,有Dωf=0(fDω=0),则称f为Ω上的加权左(右)正则函数.也简称加权左正则函数为加权正则函数. 定义2.2对于Rn内任意两点ξ=(ξ1,ξ2,···,ξn)和x=(x1,x2,···,xn)定义它们之间的非欧氏距离ρ为 其中Aij是矩阵A的元素. 对于Rn内任意两点x,ξ,当x/=ξ时,设它们之间的欧氏距离为r,即r=|x −ξ|,则有x −ξ=ry(|y|=1),把此点y和(0,···,0)之间的非欧氏距离记作ρ0,则可以证得ρ0≥c>0. 这是因为y=(y1,···,yn)∈Rn且|y|=1,从而则 又根据ρ0的定义,显然ϕ(u1,···,un)还可以表示为下式 从而得到ρ=rρ0.又ρ0≥c,则 其中ωn表示Rn中单位球的表面积. 设Ω,∂Ω如上所述,对于任意ξ ∈Ω,以ξ为心,ε为半径,做n维非欧氏距离超球Uε(ξ)={x ∈Ω:ρ(x,ξ)<ε},∂Uε(ξ)的外法向量取正方向,则曲面∂Uε(ξ)的参数化方程可表示为 其中r(t)是Rn中欧氏距离下单位球的参数方程,又由于A=B−1,是对称正定矩阵,显然 且对上述参数化方程Jacobian矩阵有如下关系: 引理2.2(Green积分公式)[17,p7]设Ω,∂Ω如上所述,u,v:ΩAn是Ω上的连续可微函数,则对于加权Dω算子有如下公式成立 其中dσ=是∂Ω在坐标系{ψ1,···,ψn}下An(R)值的面积微元,N=(N1,···,Nn)是∂Ω上的外法向量,dµ是∂Ω的标量面积微元. 证由 引理2.3(Borel-Pompeiu公式)[17,p11]设Ω,∂Ω如上所述,u(x) :Ω ⊂Rn →An(R),且u(x)在Rn上连续可微,则有 引理2.4(Cauchy-积分公式)[17,p11]设Ω,∂Ω如上所述,若u是Ω内的加权正则函数,则Borel-Pompeiu公式即为Cauchy-积分公式 定理3.1(平均值定理)设Ω如上所述,若f是Ω上的加权正则函数,则对于任意ξ ∈Ω,有 证根据引理2.2和引理2.4,有 又因为f是Ω上的加权正则函数,所以对任意x ∈D ⊂Ω,有Dωf(x)=0,则上式变为 又由于矩阵AB=E,E为单位矩阵,则矩阵AB对角线上的元素的和为 从而 代入(3.2),再根据Green积分公式,有 定理3.2(最大模原理)设Ω是Rn中的域,若f是Ω上的加权正则函数,如果存在a ∈Ω,使得 对所有ξ ∈Ω都成立,则f在Ω内为常函数. 证设|f(a)|=λ.令Ωλ={ξ||f(ξ)|=λ},则由于a ∈Ωλ,则Ωλ非空.对于任意ξ ∈Ω Ωλ,有|f(ξ)|<λ,又由于|f(ξ)|在Ω内连续,则存在以ξ为心,R′为半径的n维超球D(ξ,R′)={x ∈Ω:ρ(x,ξ) 任取ξ ∈Ωλ,作n维超球D(ξ,R′′)={x ∈Ω:ρ(x,ξ) 由平均值定理,当f ≡1时,有 因此 所以对于任意x ∈D(ξ,R′′),有|f(x)|=λ,即D(ξ,R′′) ⊂Ωλ,因此Ωλ在Ω中是相对开的.又由于Ω是Rn的非空开的连通子集,所以由球连法,可得在Ω上对于任意的ξ ∈Ω,有|f(ξ)|0=λ. 当λ=0时,显然有f(ξ)=0,即f(ξ)在Ω内为常数. 对(3.3)关于ξi求偏导,有 再对(3.3)关于ξj(j/=i)求偏导,有 在(3.4)等式两边乘以Bii,再对(3.5)等式两边乘以Bij关于i,j=1,2,···,n分别进行求和,得到 展开即 根据正定矩阵B的Cholesky分解B=LLT(L是下三角矩阵,且对角线上元素Lii >0,i=1,2,···,n)则将下式 代入(3.6)得 即 从而对所有的N,有 推论3.1设Ω如上所述,若f(ξ)在内连续,在Ω内是加权正则函数,则 证如果f(ξ)是常函数,则结论成立. 假设f(ξ)是非常函数的加权正则函数,由于Ω是有界域,且f(ξ)在内连续,则存在点a ∈使得 如果a ∈∂Ω,则 则结论成立. 假设a ∈Ω,则将Ω分解为Ω=Ω1∪Ω2∪···,其中Ωj是有界的连通开集,j=1,2,···,则存在j使得a ∈Ωj,由于对于任意ξ ∈Ωj,有|f(ξ)| ≤|f(a)|,f(ξ)是加权正则函数,根据定理3.2,则f(ξ)在Ωj内为常函数,与已知矛盾,因此 即 推论3.2设Ω如上所述,若f(ξ)在Ω内是非常量的加权正则函数,则对Ω内任意一点ξ,有 定理3.3设Eω(x,ξ)如上所述,则存在M0,使得 对所有(α1,α2,···,αp)∈{1,2,···,n}p成立. 证利用数学归纳法证明. 又由于AB=E,则 从而上式化简为 且由于 则存在M4>0,使得 假设j ≤p −1时成立,即 下证j=p时,成立 事实上 下面首先讨论I1.若α1,α2,···,αp−1中存在一数与αp相同,不妨设αp−1=αp,则 由假设存在M6>0,M7>0,使得 则有 即存在M8>0,使得 若α1,α2,...,αp−1任何数都不等于αp,则有 综上,由归纳假设可知,存在M0使得 从而 对所有 都成立. 定理3.4 (Weierstrass定理)假设{fj}(j是正整数)是Ω中的一列加权正则函数列,如果对Ω中的每个紧集K,任意ε>0,存在自然数N(ε,K),使得 则存在Ω上的函数f,使得 (i)f是Ω中的加权正则函数; (ii)对任意多重指标β,函数列{∂βfj}(j是正整数)在Ω上是内闭一致收敛于∂βf. 证设K是Ω中任意一个紧集,令序列Kj(j=1,2,...)是Ω的一个正规穷竭,满足Kj是紧集,j=1,2,...;则存在i0,使得K ⊂Ki0. 由加权正则函数的Cauchy积分公式,以及fi −fj是Ω中的加权正则函数,从而对所有ξ ∈K和多重指标β有 则当i,j ≥N(ε,K)时,有 有界,因而存在M11>0,使得 又由定理3.3可知 则 对于fi,fj的各个元素,i,j=1,2,···,有 这表明∀N ∈Γn,序列{fj,N(ξ)}(j=1,2,···,) 是E(Ω,R)中的Cauchy列,其中E(Ω,R)是定义在Ω上取值于R的函数全体构成的集合,则由E(Ω,R)的完备性可知,存在函数fN ∈E(Ω,R),N ∈Γn,使得{∂βfi,N(ξ)}在Ω中内闭一致收敛于∂βfN(ξ),β为任意多重指标. 再令f=从而{∂βfi(ξ)}在Ω中内闭一致收敛于∂βf(ξ),当β=1,{∂fi(ξ)}在Ω中内闭一致收敛于∂f(ξ),从而有{Dωfi(ξ)}在Ω中内闭一致收敛于Dωf(ξ).由Dωfi(ξ)=0(i=1,2,···),从而Dωf(ξ)=0,所以f是Ω中的加权正则函数.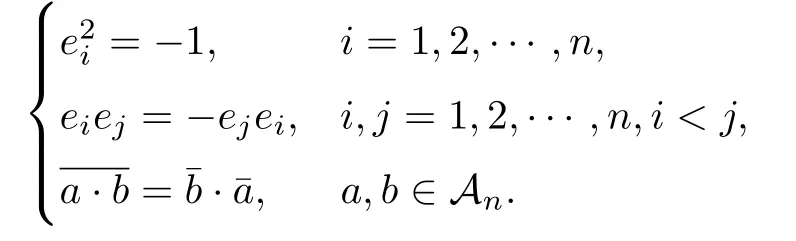
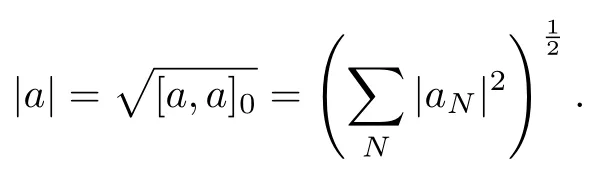
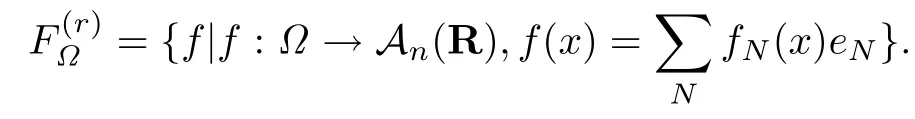




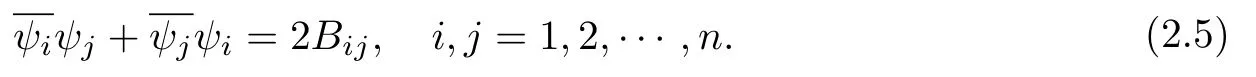
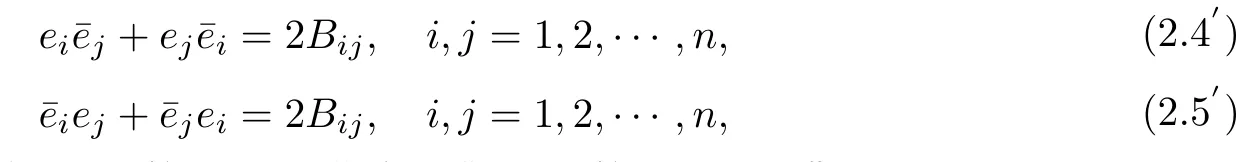



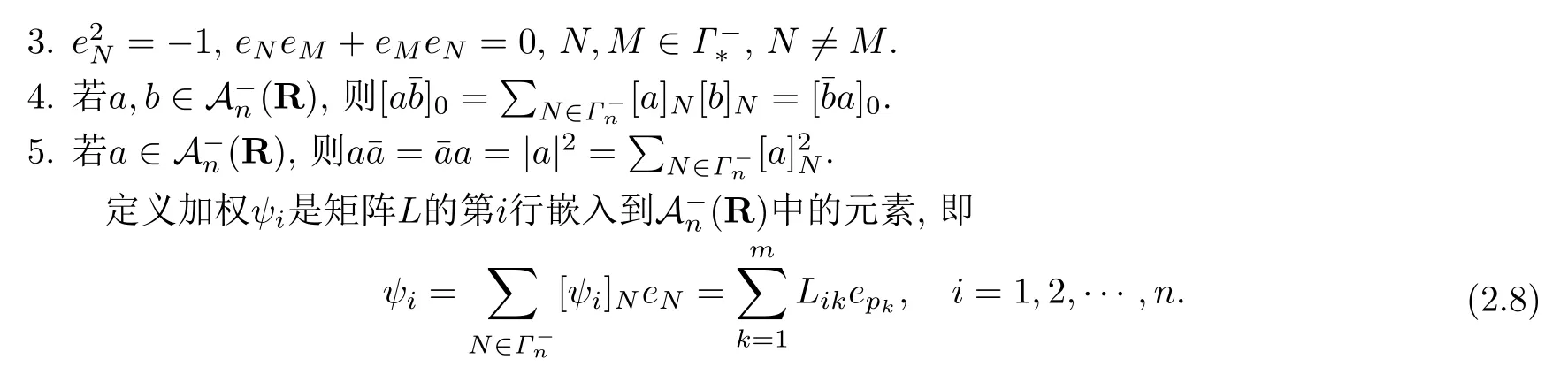
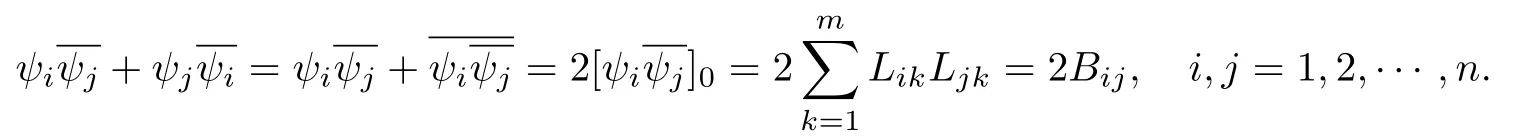
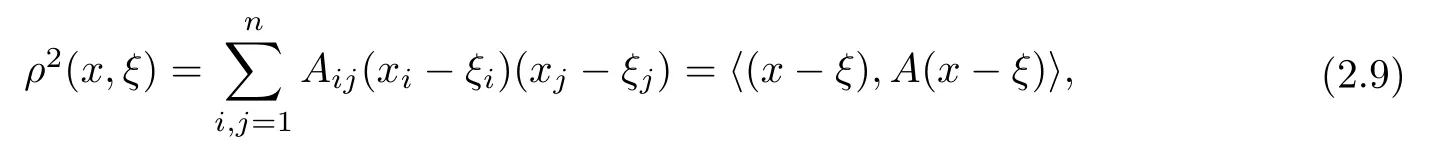

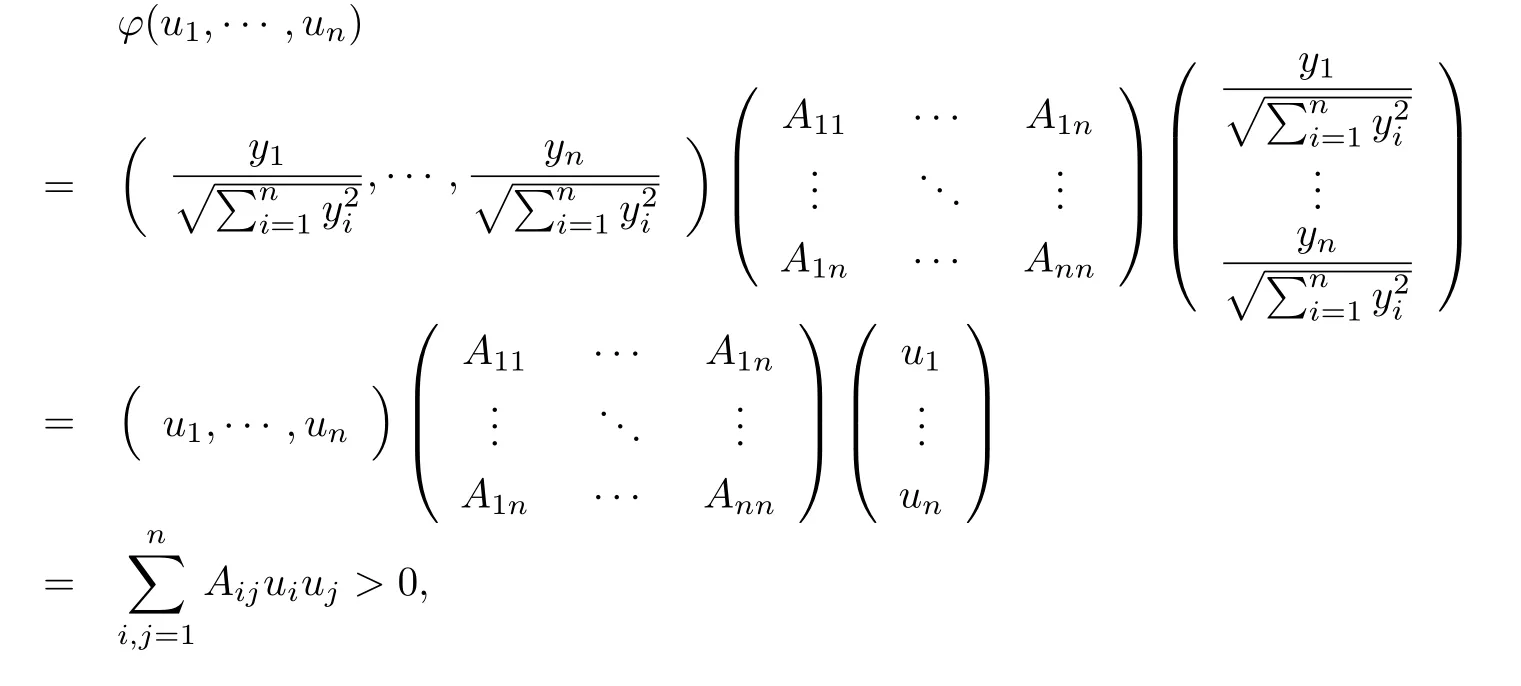











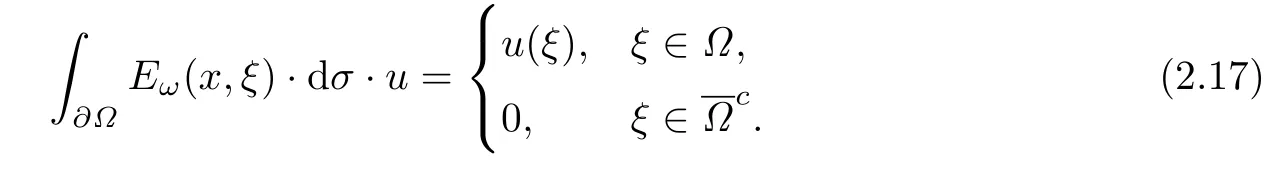
§3 加权正则函数的有关性质