再生核希尔伯特空间连续线性泛函的范数及其应用
王揄辰,杨士俊
(浙江工商大学 统计与数学学院,浙江杭州 310018)
§1 引言
再生核希尔伯特空间(Reproducing Kernel Hilbert Space,简写为RKHS)因其丰富的几何内容和再生性而被广泛地使用于统计学习,统计学,人工智能,人脸识别和初值问题等广泛的领域.
因其广泛的应用,对它本身的研究也是值得提倡的.本文旨在研究再生核希尔伯特空间上连续线性泛函的范数及其简单的应用.
本文考虑再生核希尔伯特空间连续线性泛函的范数,给出其简单表示,从而以新视角得出王兴华和韩丹夫[1],Gavrea 和Ivan[2](其实[2]的主要结果跟[1]的结果一样)的文章中的结果.从而以新的视角解释其结果,在这样的框架下或许可以纳入更多的内容,如初值问题的解.
§2 预备知识
设X是一非空点集,H是定义于X的实希尔伯特空间(本文的结论也适用于复希尔伯特空间的情形,为方便计,仅考虑实希尔伯特空间的情形),H具有再生核K(x,y),即
(i)∀y ∈X,K(x,y)∈H,
(ii)∀f ∈H和y ∈X,有

其中〈·,·〉H表示空间H上的内积.在不至于引起混淆的情形下,下文将以〈·,·〉代替〈·,·〉H.
§3 主要结果
设L是定义于再生核希尔伯特空间H[3]上的连续线性泛函,首先有
定理1设H是再生核希尔伯特空间,其再生核为K(x,y),L是定义于H上的连续线性泛函,则

且

其中LxK(x,y)=L(K(·,y)),即y固定,线性泛函L作用在x的函数K(x,y)上.
证由Fréchet-Riesz表示定理知,存在f0∈H,使得

且

所以由式(3)和再生性得

故由式(3)得L(f)=〈f(y),LxK(x,y)〉=〈f,L K(·,y)〉.且由式(4)有
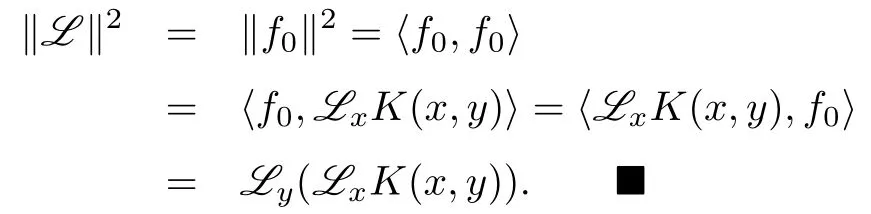
注从证明中可以看出,L K(·,y)是再生核希尔伯特空间的“表示子”(representer).
现设n ∈N+,记
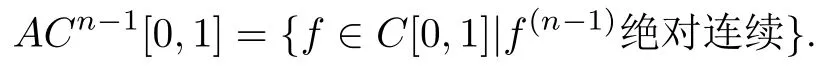
设H1={f ∈ACn−1[0,1]|f(n) ∈L2[0,1],f(i)(0)=0,i=0,1,···,n −1.}.对m ∈N+,记
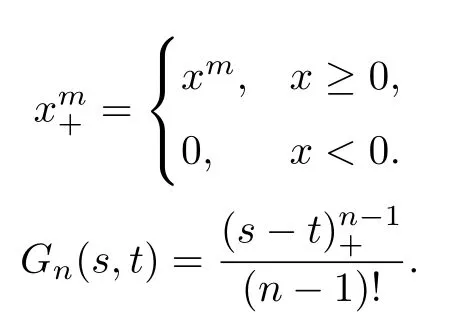
下面的命题3.1来自于Wahba[4].
命题3.1 记号如前.∀f,g ∈H1,定义其内积为则H1是再生核希尔伯特空间,具有再生核
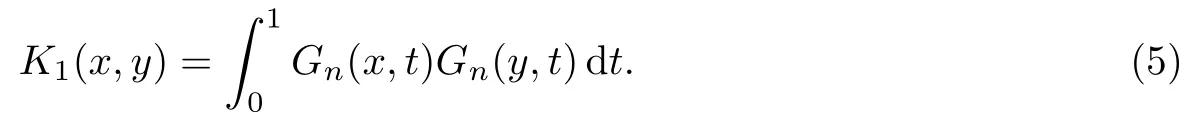
命题3.2 在命题3.1的意义下,希尔伯特空间H1的再生核可以表示为

证由命题3.1知,H1是再生核希尔伯特空间,且显然
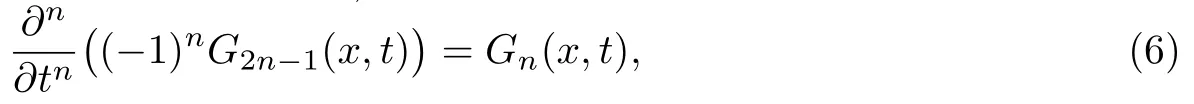
且∀f ∈H1有

所以对于(−1)nG2n−1(x,·)∈H1,由(5)-(7)得到

以下内容是熟知的,为方便计,把它写成命题3.3,参见Wahba[4].
命题3.3 令H=H0⊕H1(其中H0,H1的意义如前),其内积可以很自然地定义为

如此H0⊥H1,且K(x,y)=K0(x,y)+K1(x,y)是H的再生核.
如果进一步H0是某一有界线性泛函J的零化空间,则由前述定理1可得如下推论3.1.
引理3.1 设J是再生核希尔伯特空间H上的有界线性泛函,且
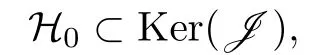
即∀f ∈H0,J(f)=0,则
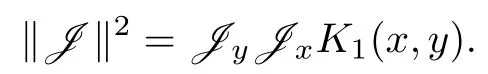
证∀f ∈H,由定理1有
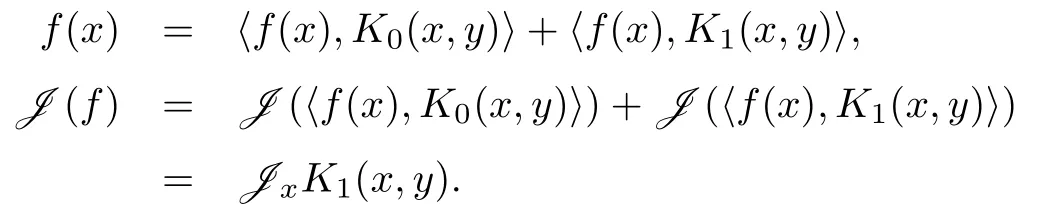
所以由定理1及其证明知‖J‖2=JyJxK1(x,y).
§4 应用
例4.1 Smale[5]讨论分析算法效率和计算复杂性时涉及数值分析的诸多方面,特别地,他把数值积分的计算复杂性的理论框架建立于某一希尔伯特空间,而数值积分的计算复杂性就依赖于该希尔伯特空间的某一有界线性泛函的范数.下面将说明,其作为数值积分框架的希尔伯特空间是再生核希尔伯特空间.
设H0,H1,H的意义同命题3.3,J是再生核希尔伯特空间H的有界线性泛函,且J(g)=0,∀g ∈H0,则由命题3.2和推论3.1得到

这给出了王兴华和韩丹夫[1]中引理1,从而可以给出Smale[5]意义下数值积分的计算复杂性.
例4.2 若J满足命题3.2和推论3.1的条件,则
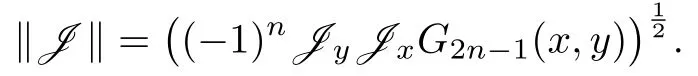
再由|J(f)|≤‖J‖‖f(n)‖得
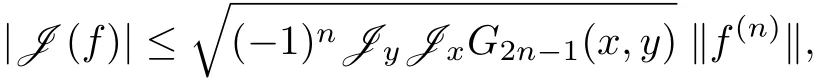
这就是Gavrea和Ivan[2]的主要结论,其泛函证明参见崔峰-杨士俊[6].

