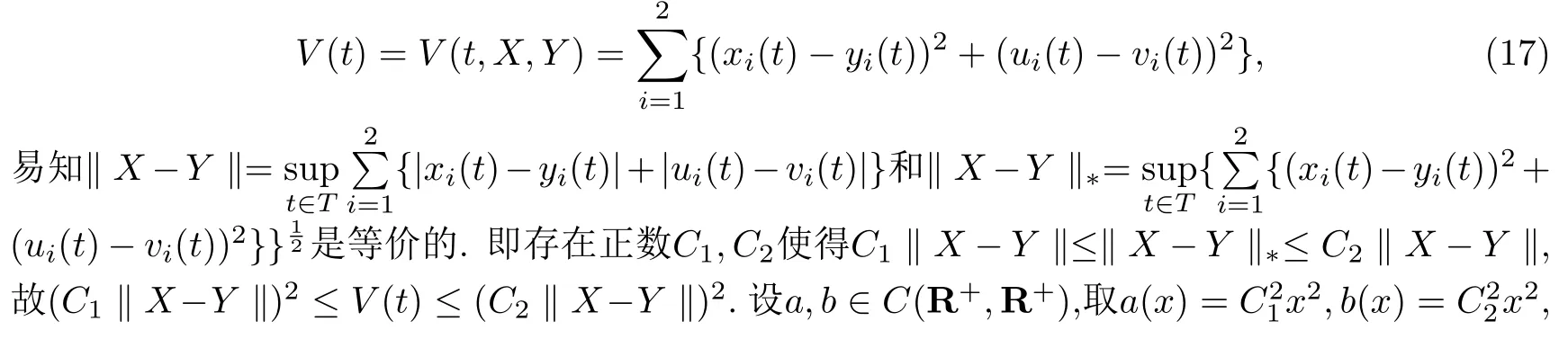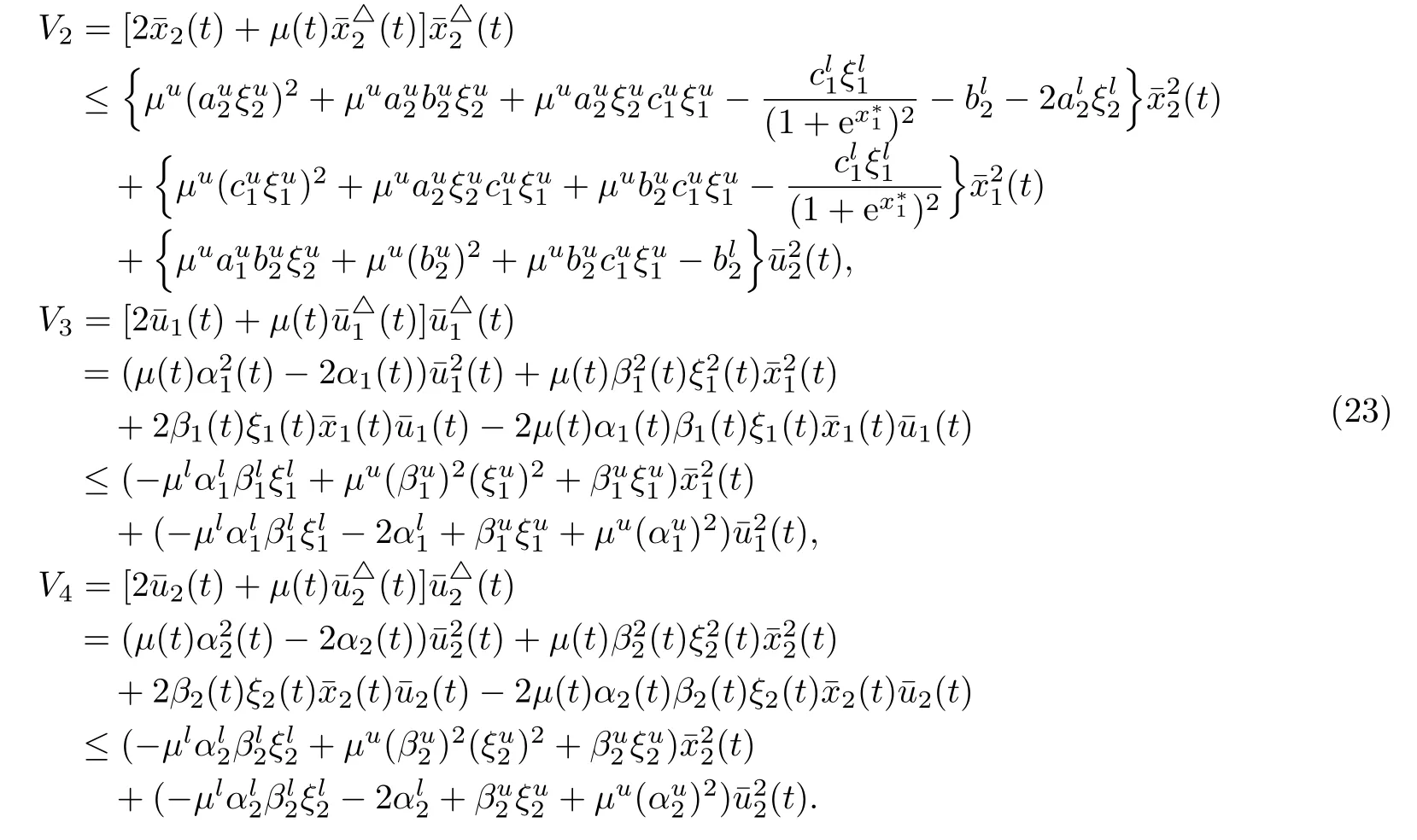时标上带有反馈控制的两种群竞争系统的概周期解

2022-03-14 04:00鲁红英

高校应用数学学报A辑 2022年1期

鲁红英

(东北财经大学数据科学与人工智能学院,辽宁大连 116025)

§1 引言

竞争系统在种群生态学中起着十分重要的作用,它描述了自然界中生物种群的内部联系,历来受到学术界的关注(如文[1-5]及其参考文献).因此,许多学者对自治或非自治竞争系统的动力学行为进行了深入的研究(如文[6-10]及其参考文献).1992年,Gopalsamy提出了自治两种群竞争系统[11]

其中xi(i=1,2)是竞争种群Xi的种群密度.ri(i=1,2) 是种群Xi的内秉增长率,ai,ci(i=1,2)分别是种群Xi内部竞争和种群Xi间竞争的强度.覃文杰,刘志军等[12]提出了系统(1)的离散模型,得到了存在唯一全局渐近稳定正周期解的条件.在种群动力学中,控制变量已被广泛应用于描述影响生物种群的生存率,死亡率等特征的干扰因素,故种群生态系统中引入反馈控制变量是有非常深刻的实际意义的.因此,近些年许多学者分别对具有反馈控制的连续竞争系统和离散竞争系统的渐近行为进行了深入广泛的研究(如文[13-16]及其参考文献).于刚等[17]在系统(1)的基础上，提出了具有反馈控制的非自治离散两种群竞争模型,研究了该系统概周期解的存在性和稳定性问题,得到存在唯一的一致渐近稳定正概周期解的充分条件.

在1988年,德国数学家Stefan Hilger建立了时标理论,该理论在连续分析和离散分析之间架起了桥梁.此外,如果不能单一用差分方程和微分方程准确描述一些受到环境影响的生物种群时,那么在时标上描述该生物种群生长规律,即通过选取合适的时标,就可以建立更加有效的种群动力学系统.如:昆虫繁殖,神经网络,热传导和传染病等模型.因此,时标理论不仅整合和统一了差分方程和微分方程理论,而且还拓展了种群动力学的研究范畴.时标上的种群动力系统研究已成为一个新热点,相继有许多学者对时标动力学系统的稳定性,振动性,周期性和边值问题等渐近行为进行了研究,得到了很好的研究成果(如[18-28]).目前,关于具有反馈控制两种群竞争系统的概周期解研究大多集中于连续系统和离散系统概周期解的存在性问题.对于在时标上讨论两种群竞争系统概周期解结论还很少.基于以上考虑,本文将研究时标T上带有反馈控制的两种群竞争系统

其中t ∈T,T为概周期时标,ui(t)是关于种群Xi的控制变量,ri(t),ai(t),bi(t),ci(t),αi(t),βi(t) 都是时标T上的非负有界概周期函数.

对定义在T上的任意非负有界概周期函数{f(t)}引进记号

系统(2)满足如下基本假设.

(H1)ri(t),ai(t),bi(t),ci(t),αi(t),βi(t)(i=1,2)都是时标T上的非负有界概周期函数,即对任意i=1,2有

其中R+是T到R的正回归函数集合.

考虑从生物学意义出发,本文主要讨论系统(2)的正解,因此假设系统(2)的初始条件为

本文主要目的是研究系统(2)的概周期解,运用文献[18-20]的分析技术和基于系统(1)持久性结果,运用概周期函数性质和构建合适的lyapunov函数,得到存在唯一一致渐近稳定正概周期解的一组充分条件,并且可以将所得到的结论应用到相应的连续与离散竞争系统中,这样就把连续与离散分析整合与统一了起来.

§2 预备知识

文中的一些基本概念和引理引自文献[18-21].

定义2.1若时标T满足

称T为概周期时标.

定义2.2T是概周期时标,函数f:T→Rn称为概周期函数,如果ε>0,集合

关于T对ε >0是相对稠密集,即对任意ε >0存在一个整数l(ε)>0使得每个长为l(ε)的区间总包含一个τ=τ(ε)∈E(ε,f),使得|f(t+τ)−f(t)| <ε,∀t ∈T.则集合E(ε,f)称为f(t)的ε−不变集,称l(ε)为f(t)的ε−不变数.

定义2.3若对于系统(2)的每一个解(x1(t),x2(t),u1(t),u2(t))T,存在正常数使得

成立,则称系统(2)是持久的.

引理2.1若p,q:T→R是两个回归函数,则

引理2.2若f,g:T→R在t ∈Tk处△可导,则

(1) 对任意常数a,b有,(af+bg)△=af△+bg△;

(2) (fg)△(t)=f△(t)g(t)+f(σ(t))g△(t)=f(t)g△(t)+f△(t)g(σ(t));

(3) 若f△≥0,则f是增函数.

引理2.3若f,g ∈C(T,R)的概周期函数,则

(1)f+g,fg也是概周期函数;

(2)f,g在T上是有界的.

引理2.4函数f(t)是概周期函数当且仅当对任意序列存在子列{hn}⊂使得函数f(t+hn)关于t ∈T一致收敛,n →∞.

引理2.5令−a ∈R+.

(1)如果x△(t)≤b −ax(t),那么

(2)如果x△(t)≥b −ax(t),那么

§3 持久性

下面将给出系统(2)持久性的一组条件.

引理3.1假设(H1)成立,则系统(2)的解(x1(t),x2(t),u1(t),u2(t))T满足

证若(x1(t),x2(t),u1(t),u2(t))T为系统(2)的任一个解.对∀x ∈ R,应用Bernoulli不等式ex ≥1+x及系统(2)的第一个方程和第二个方程得

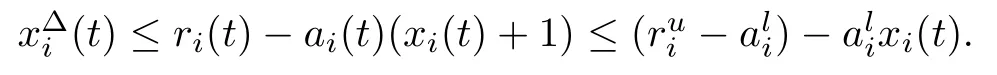
由引理2.5易知

由(4)式,对于∀ε>0,存在T1∈T,当t ≥T1,有

类似地,讨论系统(2)的第三个方程和第四个方程有

故由引理2.5得

令上式中ε →0可得

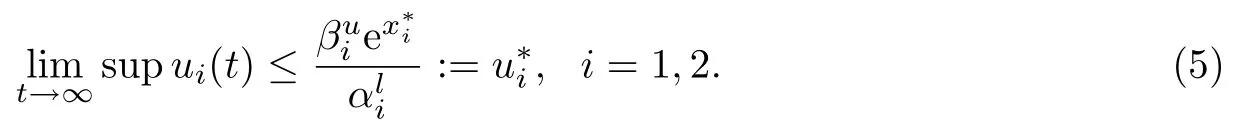
引理3.2假设(H1)和(H2)成立,则系统(2)的解(x1(t),x2(t),u1(t),u2(t))T满足

证若(x1(t),x2(t),u1(t),u2(t))T为系统(2)的任一个解.由引理3.1知,存在一个T2∈T,当t ≥T2>T1,有

基于系统(2)的第一个方程和第二个方程

断定对t ≥T2,i,j=1,2,i/=j,有

因此

令(9)中ε →0,则

由(10)式,对于∀ε>0,存在T3∈T,当t ≥T3,有

由系统(2)的第三个方程和第四个方程有

于是由引理2.5得

令ε →0,由(11)可得

证毕.

由引理3.1和引理3.2,得到系统(2)持久性结果.

定理3.1假设(H1)和(H2)成立,则系统(2)是持久的.

§4 正概周期解存在唯一性

考虑时标上非线性概周期系统

这里f:T×SB →R,SB={x ∈R:‖ x ‖0

引理4.1[17]函数V(t,x,y)定义在T+×SB ×SB上,满足如下条件(i)-(iii).

(i)a(||x −y||0)≤V(t,x,y)≤b(||x −y||0),其中a,b ∈ℛ={a ∈C(R+,R+):a(0)=0,a是递增函数};

(ii)||V(t,x1,y1)−V(t,x2,y2)||≤K{||x1−x2||+||y1−y2||},K >0是一个常数;

(iii)△V(13)(t,x,y)≤−cV(t,x,y),这里c>0,−c ∈R+.

此外,当t ∈T+时,若系统(13)有一个解x(t)∈S,其中S ⊂SB是一个紧集,则系统(13)存在唯一的一致渐近稳定概周期解p(t),且p(t)∈S.而且若f(t,x)是ω周期的,则系统(13)有唯一的一致渐近稳定的ω周期解.

设集合Ω为系统(2)的所有解(x1(t),x2(t),u1(t),u2(t))T构成的集合,对于t ∈T满足xi∗≤xi(t)≤,ui∗≤ui(t)≤由定理3.1易知集合Ω为系统(2)的不变集.

引理4.2若系统(2)满足条件(H1)和(H2),则Ω/=∅,即系统(2)至少有一个有界的概周期解.

证由条件(H1)可知ri(t),ai(t),bi(t),ci(t),αi(t),βi(t)(i=1,2),都是时标T上的概周期函数,则存在一个序列τn ⊆T当n →+∞,τn →+∞有

由定理3.1可知,存在一个t1∈T使得当t ≥t1时有

当t ≥t1−τn,n=1,2,···,i=1,2,记xin(t)=xi(t+τn)和uin(t)=ui(t+τn).对任意的正整数m,取{xin(t) :n ≥m}和{uin(k) :n ≥m}的子列,使得它们在时标T上的任意有限区间上分别收敛.不失一般性,仍记其收敛子列为{xin(t)}和{uin(t)}.因此,存在序列{yi(t)}和{vi(t)},i=1,2,当n →+∞,t ∈T时,xin(t)→yi(t),uin(t)→vi(t).显然Y(t)=(y1(t),y2(t),v1(t),v2(t))T是系统(2)的一个解,且满足