带缺失数据的偏正态众数回归模型的参数估计

谭佳玲,曾 鑫,吴刘仓

(昆明理工大学理学院,云南昆明 650504)

§1 引言

现实问题中,数据几乎都具有偏斜,完全对称情况十分罕见.若忽略偏态特征,会导致结论偏倚,降低效率.实际上,数据的偏斜特征能够由偏态分布描述,过去的大量研究表明,使用偏正态分布有效解决了数据偏斜问题.另外,数据常因各种各样的原因产生缺失.例如,在抽样调查与实验中,数据受到无回答的干扰,或由人为原因导致缺失.目前对均值建模的理论已十分成熟,在偏正态数据下,为了更好地认识众数的性质,对众数建模是有意义的.

近年来,对缺失与偏态数据的研究已经取得一定成果.在缺失数据方面,对缺失值进行插补是处理缺失值的方法之一,杨晓倩[1]将缺失数据的插补方法进行了分类,同时比较各种插补方法的插补效果,明确了插补方法的选择需要依靠不同数据特性具体分析;廖祥超[2]讨论了九种常用的插补方法,系统地介绍了插补方法的使用,并基于已知数据集从插补误差与建模效果两方面比较了插补效果;Hadeed等[3]利用短期监测到的空气污染数据,研究数据缺失问题与缺失值的估算方法.在偏正态数据方面,Azzalini[4]首次对偏正态分布做了系统研究,提出了含偏度与峰度的偏正态分布.之后,Azzalini[5]简单讨论了数据服从偏正态分布时,如何进行回归分析.后续许多学者在偏正态数据下研究了回归模型.例如,Ferreira等[6]研究了偏正态线性回归模型的诊断分析,简化了EM算法中条件期望表达式的求解.Hu等[7]基于偏正态部分函数线性模型进行统计推断,提出了基于函数主成分分析的极大似然估计方法,并检验了方差齐次性.

随着缺失数据与偏态数据领域的研究越来越成熟,部分学者开始将二者结合起来.例如,Lin等[8]对数据不完全的多元偏正态模型进行分析,并在随机缺失机制下,提出了一种解析简单的ECM算法,用于计算参数估计,同时使用单值插补的方法填补缺失值.Liu和Lin[9]研究了不完全数据下的偏正态因子分析模型,提出了一种分析可行的ECM算法,用于随机缺失机制下的参数估计.另外,吴刘仓等[10]研究了在带有缺失的偏正态数据下线性回归模型的统计推断,比较了几种插补方法的插补效果.吴刘仓等[11]分别基于偏正态分布,偏t正态分布,研究了联合均值与方差模型的插补方法与参数估计.

综上所述,目前对于偏态数据有一定的研究,对缺失数据的研究较为丰富,基于缺失数据进行统计推断的理论较为成熟.虽然带有缺失的偏正态数据的回归模型也有一定的研究成果,但在带有缺失的偏正态数据下众数回归模型的统计推断问题涉及很少.原因之一在于虽然一维偏正态分布适用于研究数据呈单峰且有偏的情形,但在参数模型的框架下,对众数建模需要知道分布的众数的显示表达.考虑到众数作为“最多水平”的标志值,在偏正态数据下对众数建模是有意义的,曹幸运等[12]在偏正态数据下针对众数建立了回归模型,研究了该模型的统计诊断问题.此外,就插补方法而言,虽有学者提到了变量服从偏正态分布时可采用众数作为插补值,但还没有学者在回归模型中进行插补效果试验.

本文的结构安排如下:§2介绍偏正态分布的性质,提出众数回归模型;§3利用高斯牛顿迭代法对模型参数进行极大似然估计;§4通过Monte Carlo 模拟证实本文所提方法的有效性;§5对实例进行分析,论证本文所构建的模型与使用的方法是合理可行的;§6给出本文的结论.

§2 偏正态数据下的众数回归模型

根据Azzalini[4]对于偏正态分布的研究,若随机变量Y服从偏正态分布,将其记为Y ∼SN(µ,σ2,λ).其中,µ为位置参数,σ2为尺度参数,λ为偏度参数.偏正态分布的概率密度函数表示为

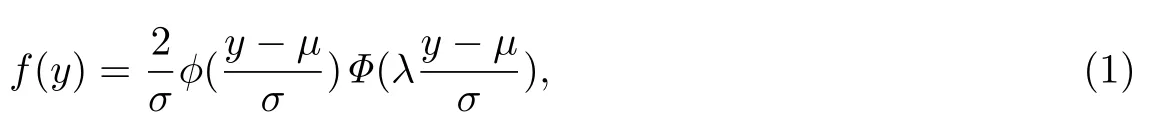
其中,φ(·) 和Φ(·)分别表示标准正态分布的概率密度函数和累积分布函数.

Azzalini的研究结果[12]表明偏正态数据的众数是唯一的,并且给出在一般情况下,众数的计算式为Mode(Y)=µ+σM0(λ).对于一般的λ而言,很难得到M0(λ) 的显式表达式,于是采用数值方法去近似它.Azzalini[12]提出一种简单但实际上十分精确有效的近似

2.1 偏正态分布的随机表示

依据Henze[14]的研究,定义随机变量Z是具有密度函数φ(y;λ)=2φ(y)Φ(yλ) 的连续随机变量,也就是Z ∼SN(0,1,λ),可描述随机变量Y的表达式为Y=µ+σZ.进而可以得到随机变量Y的随机表示(SR)为

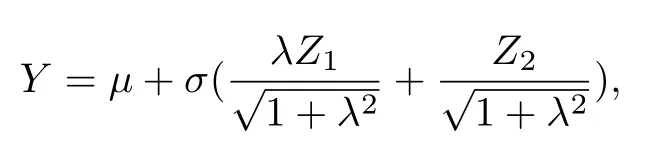
上式有Z1∼TN(0,1;(0,+∞)),Z2∼N(0,1),其中TN(·) 表示标准正态分布在区间(0,+∞)上的截尾,则Y服从位置参数µ,尺度参数σ2,偏度参数λ的偏正态分布.

2.2 偏正态众数回归模型

由众数计算式Mode(yi)=µi+σM0(λ)与回归模型(2),可知位置参数的表达式为

其次,根据式(1)和式(3),可得yi的概率密度为

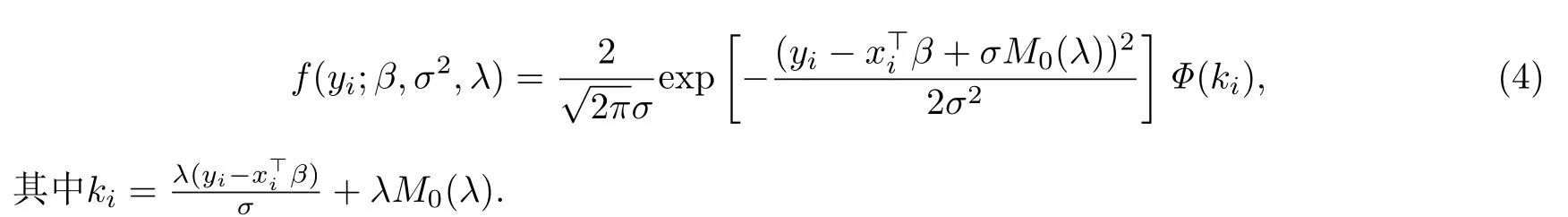
在以上模型中,yi为第i个响应变量,服从位置参数为µi,尺度参数为σ2,偏度参数为λ的偏正态分布.xi=(xi1,···,xip)是可以观测的协变量,β=(β1,···,βp)是维数为p×1维的未知众数回归系数.

§3 偏正态数据下众数回归模型的参数估计

3.1 完全偏正态数据下的极大似然估计

对于众数回归模型,由式(3)与(4)可得似然函数为

并令θ=(β,σ2,λ),则对数似然函数L(β,σ2,λ)为

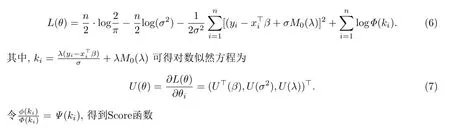
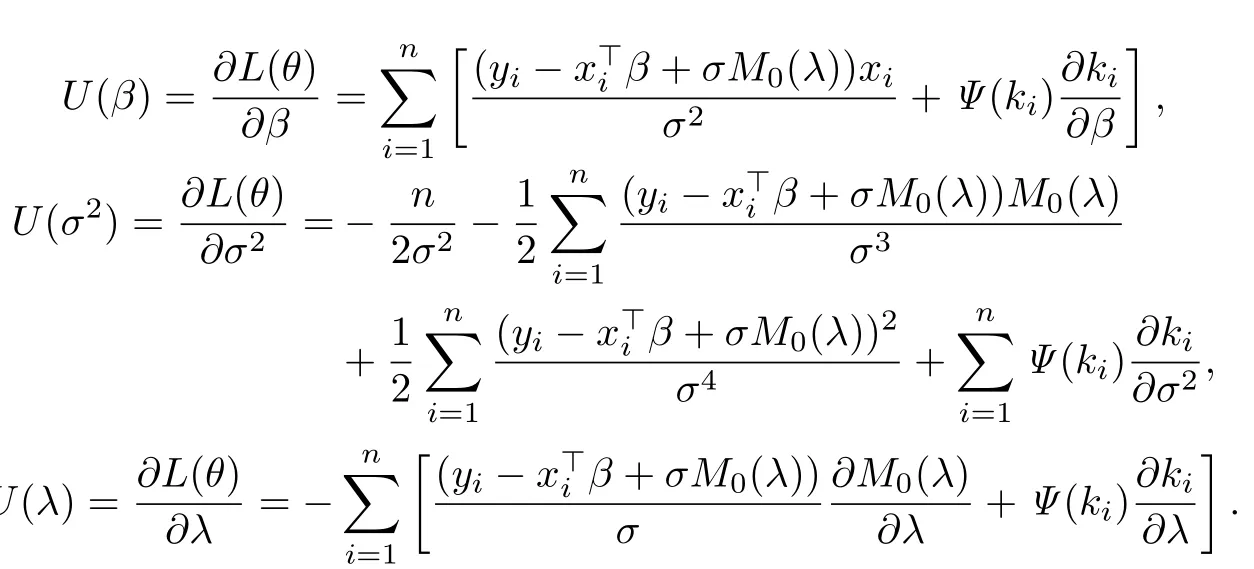
对数似然函数L(θ)关于参数θ=(β,σ2,λ)的Hessian矩阵为

步骤1更新θ(1)=θ(0)+D(θ(0));

步骤2将θ(1)记为当前迭代,更新θ(2)=θ(1)+D(θ(1));

···

步骤3重复迭代至第t次,将θ(t)作为当前参数再迭代,得到θ(t+1)=θ(t)+D(θ(t));

步骤4直到||θ(t+1)−θ(t)||2≤η,η为预定的充分小的正数,如η=10−6,则认为迭代收敛,取θ(t+1)作为极大似然估计的近似值.

3.2 带有缺失的偏正态数据下的极大似然估计

缺失机制一般分为三类,分别是完全随机缺失,随机缺失与非随机缺失.在对含有缺失数据的数据集进行处理之前,明确数据的缺失机制是必要的.本文为了比较插补方法,选取随机缺失作为缺失机制.缺失数据下的参数估计方法之一是将缺失数据集通过选用的插补方法补全后,应用高斯牛顿迭代法进行极大似然估计.

接下来介绍采用的几种插补方法,首先约定无缺失数据的样本点为有应答项,则有缺失数据的样本点为无应答项.定义f为应答变量,表示目标样本中是否存在缺失项.fi=1为第i个单元有应答,不存在缺失项.fi=0为第i个单元无应答,存在缺失项.y为目标变量,称为插补值,则插补后的完全数据为

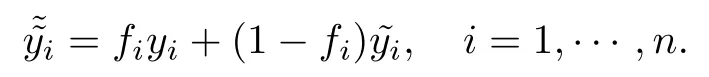
(1)均值插补(EI)

均值插补[1]指在缺失数据集中,计算目标缺失变量中有应答项的均值,后用该均值替代缺失数据真值.主要分为以下两种.

单一均值插补指分别计算各目标变量中有应答项的均值,然后插补到相应的缺失项中.每一目标变量只能有一个均值,用这个均值插补到对应的所有缺失项中.单一均值插补简单地利用一个均值代替缺失值,严重扭曲样本分布,总体方差与协方差被低估,不适合偏态数据下的参数估计,一般更适合变量服从或近似服从正态分布的情况.插补值理论式为

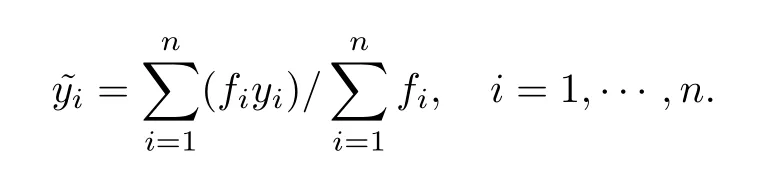
分层均值插补指在利用均值这个简单变量进行插补之前,根据变量的属性,对总体进行分层,使各层中的各项数值尽可能相近,每一层中求解单一均值,各层的单一均值分别代替各层的缺失值,得到分层均值插补数据集

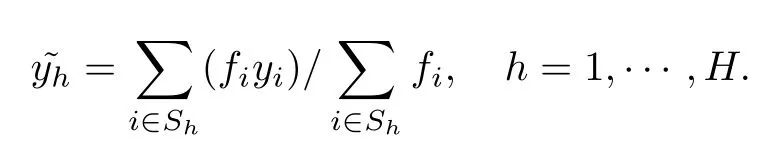
其中H表示分层总数,Sh表示第h层所在的数据集,为该层的插补值.分层的层数H需考虑缺失项多少,然后由总体样本划分适合的层距,每层之间各项数值尽可能相近.每一层对应一个单一均值,显然提高了均值插补的效果,因此在大样本的条件下,可使用分层均值插补.插补值理论式为

(2)众数插补(MI)

众数插补指分别计算各目标变量中的众数,用众数替代缺失数据真值.变量服从或近似服从偏正态分布,考虑众数作为插补值[2].插补值理论式为

众数代表了数据的大多数水平,在缺失偏正态分布数据下,根据偏正态分布的特性,数据主要集中在偏斜方向,导致均值,中位数,众数是不等的,从数据集的角度出发,采取众数作为缺失项的插补值,更适合偏正态数据下的参数估计.

(3)回归插补(RI)

回归插补[2]指先根据数据集是否含有缺失项,将其划分为两类.一是含有缺失项的缺失数据集Dmis,二是不含缺失项的完全数据集Dcom.其次,在完全数据集Dcom中,建立缺失变量Y关于辅助变量X的回归模型,最后预测缺失数据.

对于缺失变量yi ∼SN(µi,σ2,λ),给定x条件下y的密度函数为fθ(y|x),其中θ=(β,σ2,λ).将数据集按是否缺失的标准进行划分,得到完全数据集Dcom包含y1,···,yk,缺失数据集Dmis包含yk+1,···,yn.利用观测值(x1,y1),···,(xk,yk)并采用完全数据下参数的极大似然估计方法对参数θ进行估计,从而得到这样就可以对缺失值yj(j=k+1,···,n)进行独立的参数随机插补.插补值理论式为

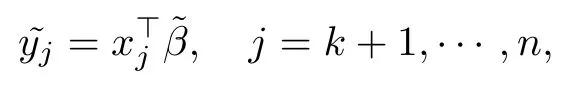
§4 Monte Carlo模拟

本节对§3提出的完全数据下模型参数的极大似然估计与利用三种插补方法插补后的缺失数据下模型参数的极大似然估计进行模拟研究.此外,模拟传统均值回归模型的参数估计,与本文提出的方法进行比较.均值回归模型下的回归系数用α表示.用均方误差(MSE)来评价估计效果,等同于权衡参数的精度,假设α0,β0,,λ0是参数α,β,σ2,λ的真值,定义均方误差(MSE)如下.

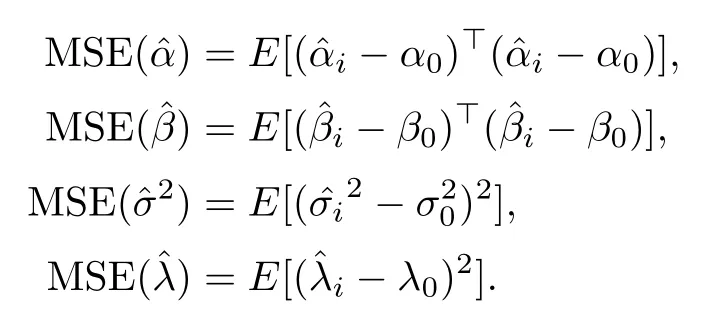
4.1 完全数据下的Monte Carlo模拟

模拟数据基于模型(2)与§2偏正态分布的随机表示得出.取参数的真值为α0=(5,−6,7),β0=(5,−6,7),=4,分别取λ0=−5,λ0=5.在完全样本量n分别为100,200,300的条件下,重复模拟1000次.模拟结果见表4.1.

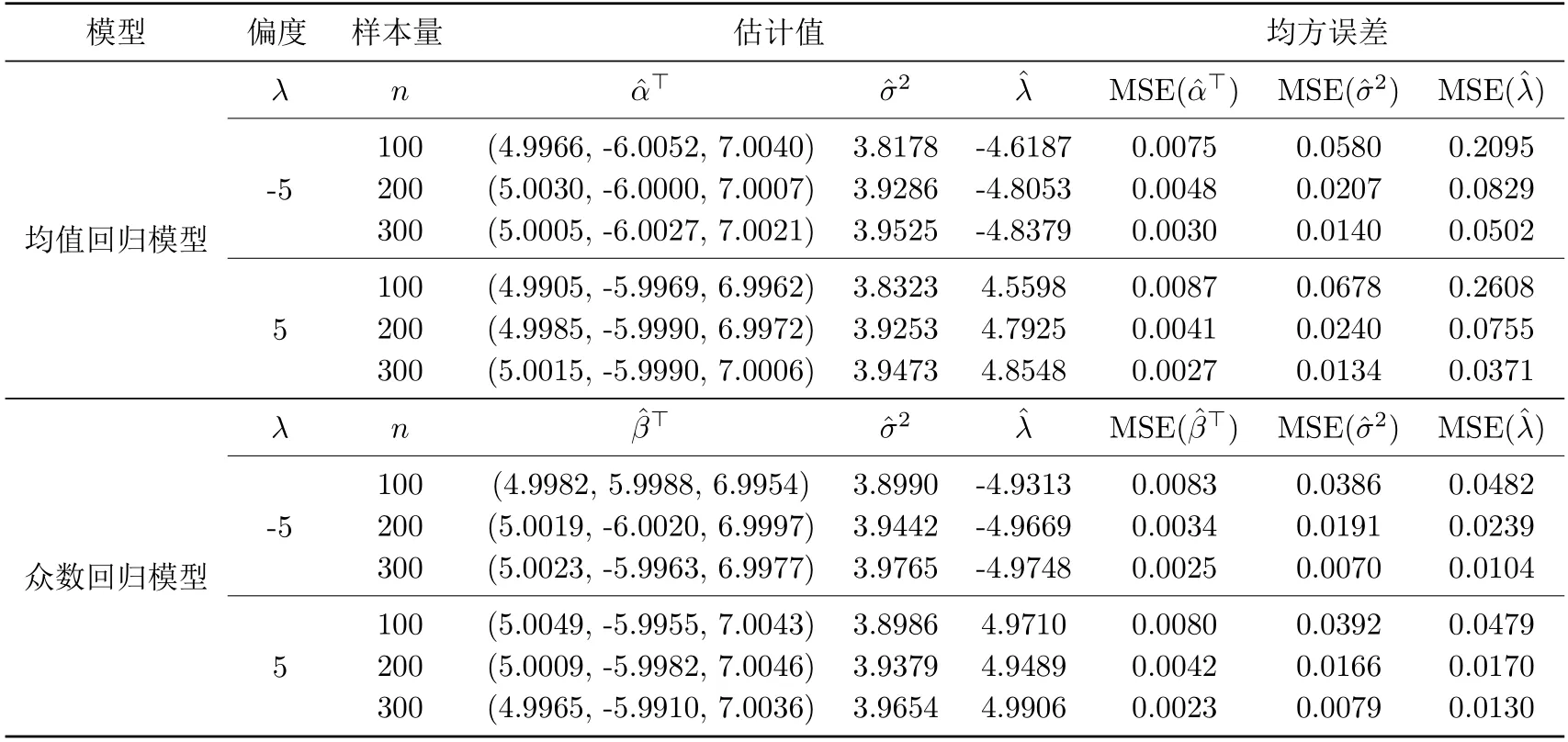
表4.1 完全数据下均值和众数回归模型的参数估计结果比较

从表4.1可知,无论偏度的取值是正还是负,随着样本量n的增大,所有参数的估计值都越来越接近真值,均方误差越来越小.特别地,样本量n相同时,众数回归模型所得估计结果对应的均方误差(MSE)小于均值回归模型所得估计结果对应的均方误差(MSE),说明本文提出的众数回归模型比传统均值回归模型更优,且取得比较理想的效果.

4.2 缺失数据下的Monte Carlo模拟

首先利用上述基于众数回归模型模拟的完全数据,对响应变量Y进行随机缺失,缺失率分别为5%,10%,20%,采用§3.2中的三种插补方法,得到插补后完全数据,其次进行极大似然估计,取参数的真值为β0=(0.5,−1.5,1),=2,λ0=0.5,在样本量n为100,300的情况下分别模拟1000次.模拟结果见表4.2.

从表4.2可以得到以下结论.

表4.2 缺失数据下众数回归模型的三种插补方法插补效果

(1) 随着若样本量逐渐增大或者缺失率逐渐减小,均值插补,回归插补,众数插补三种插补方法的估计精度越来越高,表明三种插补方法是可行的;

(2) 回归插补在缺失率低的情况下,对偏度参数λ的估计效果较好;当样本量少而缺失率高时,回归插补的插补效果很差,所得偏度参数λ与尺度参数σ2的估计值与真值偏差较大;

(3) 众数插补在不同缺失率下,对尺度参数的估计效果较好.此外,众数插补在缺失率低且样本量较大的情况下,例如缺失率为5%,样本量为300时,其回归系数的均方误差MSE()是三种插补方法中最小的.表明缺失率低且样本量较大的情况下,众数插补对回归系数的插补效果比较好.

(4) 三种插补方法所得的估计结果与未插补时所得的估计结果相比,可知当缺失率小于10%时,众数插补的插补效果较优.

§5 实例分析

体质指数(BMI)可简单通过身高与体重得出.我们关注其他身体特征因素对BMI造成的影响,数据来自Cook[16]分析的BMI数据,包含202名运动员的相关体质特征数据,该数据被收录在R软件“sn”包中的ais数据集中,是偏正态数据的典型实例.将数据集中的体质指数(BMI)作为响应变量,x1-红细胞计数(RCC),x2-白细胞计数(WCC),x3-身体肥胖百分比(Bfat),x4-去脂体重(LBM)作为解释变量,研究这几个解释变量与体质指数之间的关系.图1绘制了数据的直方图和概率密度函数曲线,利用R软件估计体质指数的偏度为=0.9465155,另外,绘制数据的正态Q-Q图如图2所示,散点存在一定程度的偏离,表明数据具有明显的偏斜,BMI数据服从偏正态分布.

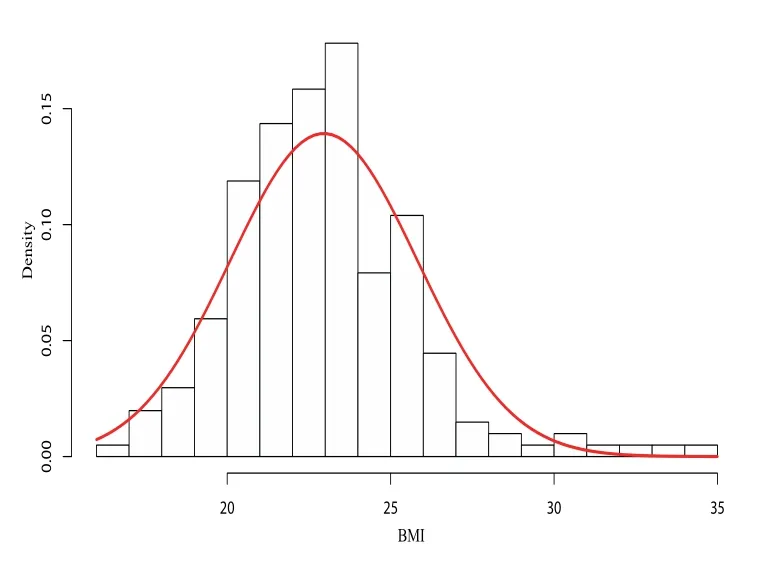
图1 BMI密度函数拟合图

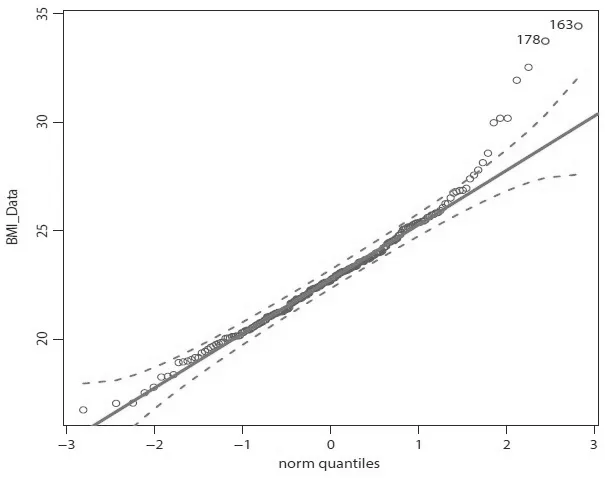
图2 BMI数据的正态Q-Q图

5.1 完全数据下的实例分析

利用该数据对偏正态分布下均值与众数回归模型做参数估计,考虑变量间关系

表5.1 均值与众数回归模型下完全BMI数据的参数估计

由上表可知,两种模型参数估计存在一定差异,表明影响均值和众数的因素不完全相同.结果显示,众数回归模型的区间估计精度优于均值回归模型,x1-红细胞计数与x3-身体肥胖百分比对响应变量y-体质指数(BMI)的均值与众数均有影响且影响相似,而x2-白细胞计数与x4-去脂体重对应的区间估计包含0,说明该变量不显著;两种回归方法对BMI数据的尺度参数σ2和偏度参数λ的估计结果相似.从实际意义来看,完整数据下的参数估计结果表明体质指数(BMI)基本不受x2-白细胞计数与x4-去脂体重的影响,实际研究人员在分析影响体质指数(BMI)的因素时,可参考此结论.

5.2 缺失数据下的实例分析

体质数据(BMI)按缺失率5%,10%,20%进行随机缺失,通过三种插补方法进行插补,应用§3.2中带有缺失的偏正态数据下的极大似然估计方法,经过100次模拟后,得到表5.2,其中,SD为算法收敛后观测信息阵主对角线元素开方所得的标准差,表示所有回归系数的标准差求和.

由表5.2可得到以下结论.

表5.2 众数回归模型下BMI实例结果

(1) 不同缺失率下,三种插补方法相较未插补情形,回归系数的估计效果都得到了提升.当缺失率从5%∼20%逐渐增大时,提升效果逐渐减小.

(2) 众数插补方法在缺失率低(5%)的情况下,相较均值插补(EI),回归插补(RI)而言,对回归系数β的估计值更接近于完全数据下的估计结果,表明众数插补在低缺失率时优于均值插补与回归插补.

(3) 不同缺失率下,均值插补与回归插补对尺度与偏度参数的估计结果基本相同.从尺度,偏度参数的角度来看,缺失BMI数据下的估计值接近完全BMI数据下的估计值.表明众数回归模型下均值插补与回归插补对尺度参数σ2,偏度参数λ的估计值更接近真实值.

§6 结论

本文基于偏正态数据构建了众数回归模型,应用高斯牛顿迭代法进行参数的极大似然估计,并将众数回归模型的参数估计结果与传统均值回归模型的参数估计结果进行了比较,模拟结果表明当数据存在偏度时,众数回归模型的估计结果都优于传统均值回归模型的估计结果.另一方面,在响应变量随机缺失的条件下,采用均值插补,众数插补,回归插补三种插补方法补全缺失数据集后,再进行参数估计,进而评价三种插补方法的插补效果.模拟结果表明,随着样本量的增大或者缺失率的减小,三种插补方法的估计精度都越来越高;众数插补在缺失率低(5%)且样本量较大的情况下,对回归系数的估计结果相较其他两种插补方法更优;在不同缺失率下,均值插补与回归插补对尺度参数,偏度参数的估计结果基本相同.实例分析的研究结果表明,三种插补方法相较未插补的情形,其回归系数的估计效果都得到提升,且缺失率为10%∼20%时提升效果更为明显.