形式背景的AE-仿紧性

吴国俊,徐罗山

(扬州大学 数学科学学院,江苏扬州 225002)

§1 引言

形式概念分析[1]是德国数学家B.Ganter和R.Wille于二十世纪八十年代初期基于序结构理论提出的一种数据分析和知识处理的方法.形式背景是形式概念分析的核心概念,它是表示知识的基本载体.近年来,形式概念分析广泛应用于机器学习,数据挖掘和信息处理等领域,激发了学者对形式概念分析的数学思考.Krtzsch在文献[2]中从范畴论角度研究了形式背景间的各种态射.除了序结构和范畴论外,拓扑学也成功地应用到形式概念分析及其特殊类型的广义近似空间理论的的研究中.李伯权等在文献[3]中讨论了形式背景属性约简和拓扑学中子基约简的关系.Pei Zheng等在文献[4-5]中对形式背景进行了拓扑式研究,在形式背景的属性集上建立了相关拓扑.杨凌云等在文献[6-8]中对形式背景在对象集上建立了多个拓扑并讨论它们之间的关系,又将拓扑空间的分离性,紧致性推广到形式背景中并推广形式背景到L-形式背景.本文进一步将拓扑空间的仿紧性推广到形式背景中,定义形式背景的AE-仿紧性,并讨论相关性质.

§2 预备知识

本文中符号P(X)表示集合X的幂集,(X,T)是一个拓扑空间,N是自然数集.

定义2.1[1]形式背景K是一个三元组(U,V,R),其中U是对象集且U中的元素称为对象,V是属性集且V中的元素称为属性.R ⊆U ×V是从U到V的一个二元关系,(x,y)∈R或xRy表示对象x具有属性y,(x,y)/∈R或xRcy表示对象x不具有属性y.

本文中,形式背景所涉及的对象集和属性集都可以是无限的,并简称形式背景为背景.

定义2.2[1]设(U,V,R)是一个背景,定义两个导出算子:α:P(U)→P(V)使得∀A ∈P(U),α(A)={y ∈V | ∀a ∈A,aRy};ω:P(V)→P(U)使得∀B ∈P(V),ω(B)={x ∈U |∀b ∈B,xRb}.对x ∈U,y ∈V,记α(x)=α({x})={y ∈V | xRy},并称之为x的对象内涵(object intent);记ω(y)=ω({y})={x ∈U |xRy},并称之为y的属性外延(attribute extent).

注2.1对于∅⊆U,有α(∅)=V;对于∅⊆V,有ω(∅)=U.若对象x满足α(x)=∅,则称x行为空行.若属性y满足ω(y)=∅,则称y列为空列.容易看出,背景(U,V,R)无空行等价于无特殊说明,约定本文涉及的背景均无空行.

注2.2[1]在背景K=(U,V,R)中,对于Ai ⊆U和Bi ⊆V(i ∈I),有

例2.1[6-7]设(X,T)是一个拓扑空间,令K∈=(X,T,∈),其中∈是通常的属于关系,则K∈是一形式背景.∀A ⊆X,∀U ⊆T,有α(A)={U ∈T | ∀a ∈A,a ∈U}={U ∈T |A ⊆ U}和ω(U)={x ∈ X | ∀U ∈ U,x ∈ U}=∩U.特别地,∀x ∈ X和∀U ∈ T,有α(x)={V ∈T |x ∈V}=为x点处的开邻域基,ω(U)={y ∈X |y ∈U}=U.

定义2.3[1]设K=(U,V,R)是背景,则称背景L=(H,N,R ∩(H ×N))是K的子背景,其中H ⊆U,N ⊆V.

注2.3为避免混淆,如没特别说明,本文将子背景L=(H,N,R ∩(H ×N))的两个导出算子分别记作α1,ω1.此处,对任意的B ⊆N,有ω1(B)={x ∈H | ∀y ∈B,xRy}.易见ω1(B)=ω(B)∩H.对于导出算子α1有类似性质.

定义2.4[7]背景K=(U,V,R)的子背景L=(H,N,R ∩(H ×N))称为嵌入子背景,如果对任意v ∈V,存在n ∈N使得ω1(n)=ω(v)∩H,其中ω1(n)是n在L中的属性外延.

例2.2设(X,T)为拓扑空间,(Y,TY)为X的子空间.则L∈=(Y,TY,∈)为K∈=(X,T,∈)的嵌入子背景.

命题2.1设形式背景K=(U,V,R)无空行.则K的任一嵌入子背景L=(H,N,R ∩(H ×N))也无空行.

证若形式背景K无空行,则=U.因L是嵌入子背景,故∀v ∈V,∃n ∈N,使ω(v)∩H=ω1(n).于是从而=H,这说明嵌入子背景L无空行.

定义2.5[6-7]设K1=(U1,V1,R1)和K2=(U2,V2,R2)是两个背景.从K1到K2的一个信息态射(文献[6]中称背景映射)(f,g)是指一对映射f:U1→U2和g:V2→V1满足∀x ∈U1,∀y ∈V2,有f(x)R2y ⇔xR1g(y).

例2.3设(X,TX),(Y,TY)是两拓扑空间,f:X →Y是连续映射.则(f,f−1)是形式背景K∈=(X,TX,∈)到形式背景L∈=(Y,TY,∈)的信息态射.反过来,若(f,g)是背景K∈=(X,TX,∈)到背景L∈=(Y,TY,∈)的信息态射,则∀V ∈TY,∀x ∈X,x ∈f−1(V)⇔f(x)∈V ⇔x ∈g(V),于是f−1(V)=g(V)∈TX,这说明f:X →Y是连续映射,且g=f−1:TY →TX.

关于形式背景的有关概念还可参见[1,9-10],关于拓扑学的基本概念可见[11-12].

§3 形式背景的AE-仿紧性

众所周知,拓扑空间X称为仿紧的是指X的任一开覆盖都存在局部有限开加细覆盖.本节在形式背景中引入AE-覆盖,AE-局部有限覆盖的概念,进而类似地定义形式背景的AE-仿紧性.

定义3.1设K=(U,V,R)是形式背景,U1⊆U.若存在B ⊆V,使得A={ω(v)|v ∈B}满足U1⊆∪A,则称A为U1的属性外延覆盖,或称A为U1的AE-覆盖.

设A和B是两个集族,称A是B的一个加细,是指A中每个成员都包含于B的某个成员中.

定义3.2[7]设K=(U,V,R)是形式背景.若∀B ⊆V,当A={ω(v)| v ∈B}满足U ⊆∪A时,总存在有限子族B ⊆A使U ⊆∪B,则称K为AE-紧致背景(文献[7]中称紧致背景).

换言之,K为AE-紧致背景当且仅当U的任一AE-覆盖均存在有限子覆盖.又容易看出,若U的每个AE-覆盖A都有一个有限AE-覆盖B是A的加细,则K是AE-紧致的.

定义3.3设K=(U,V,R)是形式背景,U1⊆U,B ⊆V,A={ω(v)| v ∈B}.若对任意x ∈U1,存在v ∈V,使x ∈ω(v)且ω(v)仅与A中有限个成员相交不空,则称A是U1的AE-局部有限集族.进一步,若A又是U1的AE-覆盖.则称A是U1的AE-局部有限覆盖.

注3.1AE-覆盖,AE-局部有限集族均是由背景的某些属性外延组成.当涉及背景K和子背景L时,使用“AE-覆盖”,“AE-局部有限集族”必须明确是在K中还是在L中.

定义3.4设K=(U,V,R)是形式背景,若∀B ⊆V,当A={ω(v)|v ∈B}满足U ⊆∪A时,总存在U的AE-局部有限覆盖B是A的加细,则称K为AE-仿紧背景.

注3.2若背景K=(U,V,R)的对象集U或属性集V是有限集,则该背景必为AE-紧致的.若背景K是AE-紧致的,则该背景必为AE-仿紧的.

在背景K∈=(X,T,∈)中,因∀U ∈T,有ω(U)=U,故有下一命题.

命题3.1拓扑空间(X,T)是仿紧空间当且仅当K∈=(X,T,∈)是AE-仿紧背景.

设集族S ⊆P(X).称S是滤向的是指,∀A,B ∈S,∃C ∈S,使得C ⊆A ∩B;称集族U ⊆S是S的下集是指,∀A ∈U,∀B ∈S,当B ⊆A时,总有B ∈U.

命题3.2设K=(U,V,R)是一形式背景,对任一x ∈U,Sx={ω(v)|x ∈ω(v)且v ∈V}是滤向的,且存在vx ∈V使x ∈ω(vx)为有限集.若V={ω(vx)| x ∈U}中每个元仅与有限个成员相交不空,则K是AE-仿紧背景.

证可断言∀x ∈U均有包含它的最小属性外延ω(ξx).事实上,对x ∈U,由条件存在vx ∈V,使x ∈ω(vx)且ω(vx)是有限集.令Ux={ω(v)| x ∈ω(v)⊆ω(vx)且v ∈V},由ω(vx)∈Ux是有限的知,Ux是Sx的非空有限子族.因Sx是滤向的且Ux有限,故存在ξx ∈V使得ω(ξx)∈Sx为Ux的下界.因Ux在Sx中是下集,故ω(ξx)∈Ux,于是ω(ξx)为Ux的最小元.由Sx是滤向的,易证ω(ξx)也是Sx的最小元,这说明断言成立.

记B={ω(ξx)| x ∈U}.设A是U上的任一AE-覆盖,则B是A的加细且覆盖U.从而B是AE-覆盖V的加细.对任一x ∈U,因x ∈ω(ξx)⊆ω(vx)且ω(vx)与V中有限个元相交不空,故对任一x ∈U,ω(ξx)仅与V中有限个成员相交不空.由B是V的加细且V中每个元都是有限集知,ω(ξx)仅与B中有限个成员相交不空.这说明B是U的AE-局部有限覆盖.综上所证,K是AE-仿紧背景.

推论3.1若拓扑空间X任一点x处都存在开邻域Vx为有限集,且V={Vx | x ∈X}中每个元仅与有限个成员相交不空,则X是仿紧空间.

证在背景K∈=(X,T,∈)中,因∀G ∈T,有ω(G)=G,故Sx={ω(G)| x ∈ω(G)且G ∈T}为x处的开邻域基由于拓扑空间X每点的开邻域基是滤向的,从而背景K∈满足命题3.2的条件,于是背景K∈=(X,T,∈)是AE-仿紧背景,由命题3.1知X是仿紧空间.

命题3.2中条件“V={ω(vx)|x ∈U}中每个元仅与有限个成员相交不空”不可缺少,否则命题不成立,反例如下.

例3.1设X=N∪{∞},T={A∪{∞}|A ⊆N}∪{∅}.取开覆盖A={{n,∞}|n ∈N},则A不存在局部有限的开加细覆盖,(X,T)不是仿紧空间,从而背景K∈=(X,T,∈)不是AE-仿紧背景.对于K∈,虽然对每一n ∈N,可取Wn={n,∞}=ω({n,∞})∈T是有限集,但集族W={ω(Wn)| n ∈N}并不满足命题3.2中条件“V={ω(vx)| x ∈U}中每个元仅与有限个成员相交”.

§4 AE-仿紧背景的性质

类似于形式背景的AE-紧致性,背景的AE-仿紧性也可被适当的信息态射所保持.

引理4.1设(f,g)是形式背景K1=(U1,V1,R1)到形式背景K2=(U2,V2,R2)的信息态射,则下列两条成立

(1) 若f是满射,则∀B ⊆V2,有f(ω(g(B)))=ω(B);

(2) 若g是满射,则∀A ⊆U1,有g(α(f(A)))=α(A).

证以(1)为例证之,(2)类似可证.若B=∅,则ω(B)=U2,ω(g(B))=U1,由f是满射,故有f(ω(g(B)))=f(U1)=U2=ω(B).若B/=∅,则对任意x ∈ω(g(B))及任意b ∈B,有x ∈ω(g(b)),即xR1g(b).因(f,g)是信息态射,故f(x)R2b,即f(x)∈ω(b),由b ∈B的任意性知f(x)∈ω(B),从而f(ω(g(B)))⊆ω(B).对任意的y ∈ω(B),由f是满射,知存在x ∈U1,使f(x)=y,于是∀b ∈B,有f(x)R2b.因(f,g)是信息态射,故xR1g(b),即x ∈ω(g(b)).注意到b ∈B的任意性,有x ∈ω(g(B)).于是y=f(x)∈f(ω(g(B))),从而ω(B)⊆f(ω(g(B))).综上所证,f(ω(g(B)))=ω(B).

定理4.1设K1=(U1,V1,R1)和K2=(U2,V2,R2)是两个背景,(f,g)是从K1到K2的信息态射,其中f是双射,g是满射.若K1是AE-仿紧的,则K2也是AE-仿紧的.

证设A={ω(v)| v ∈B}是U2的任一AE-覆盖,其中B ⊆V2.作W={ω(g(v))| v ∈B},由f是双射及引理4.1知,f(∪W)=∪v∈B f(ω(g(v)))=∪v∈B ω(v)=∪A=U2,从而U1=∪W,这说明W是U1的AE-覆盖.因为K1是AE-仿紧的,所以存在E ⊆V1,使V={ω(v)|v ∈E}是U1的AE-局部有限覆盖且加细W.由于g是满射,从而对任意v ∈E,存在sv ∈V2,使v=g(sv).令B1={sv | v ∈E} ⊆V2,并作B={f(ω(g(s)))| s ∈B1}.则由引理4.1知B={ω(s)| s ∈B1}且有∪B=∪s∈B1f(ω(g(s)))=f(∪v∈E ω(v))=f(∪V)=f(U1)=U2,从而B是U2的AE-覆盖.

断言B是A的AE-加细.事实上,∀sv ∈B1,有g(sv)=v ∈E.因V是W的AE-加细且ω(v)∈V,故存在u ∈B使ω(g(u))∈W且ω(v)⊆ω(g(u)).由引理4.1知f(ω(v))=f(ω(g(sv)))=ω(sv),f(ω(g(u)))=ω(u),从而ω(sv)⊆ω(u),由sv ∈B1的任意性及ω(u)∈A知B加细A.

下证B是U2的AE-局部有限集族.对每一y ∈U2,存在x ∈U1使y=f(x).因V是U1的AE-局部有限集族,故存在vx ∈V1使x ∈ω(vx)且ω(vx)只与V中有限个成员相交不空.因g是满射,故对vx ∈V1,存在ux ∈V2使g(ux)=vx,于是y ∈f(ω(vx))=f(ω(g(ux)))=ω(ux).由f是双射及引理4.1知对任意sv ∈B1,有如下等式

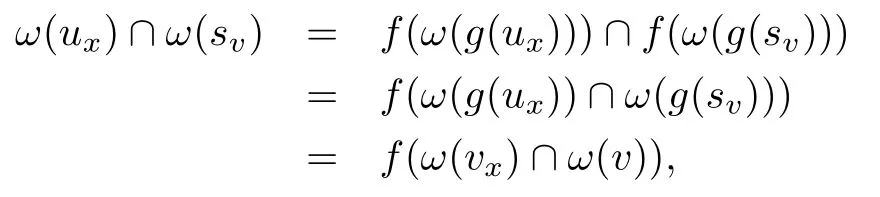
其中g(sv)=v ∈E.由此并利用ω(vx)只与V中有限个成员相交不空这一结论可推得ω(ux)只与B中有限个成员相交不空.由y ∈U2的任意性知B是U2的AE-局部有限集族.

综上,因U2的任一AE-覆盖A均有AE-局部有限加细覆盖B存在,故K2是AE-仿紧的.

下一命题利用K的属性外延给出了K的嵌入子背景L的AE-仿紧性的充分条件.

命题4.1设K=(U,V,R)是背景且L=(H,N,R ∩(H ×N))是K的嵌入子背景,若对任意B ⊆V,当A={ω(v)| v ∈B}满足H ⊆∪A时,总存在H的在K中的AE-局部有限覆盖B加细A,则L是AE-仿紧的.

证设B ⊆N及A1={ω1(v)| v ∈B}满足H ⊆∪A1.令A={ω(v)| v ∈B},显然A是H的在K中的AE-覆盖.由命题假设知存在H的在K中的AE-局部有限覆盖B={ω(v)|v ∈B1}加细A,其中B1是V的某子集.令B1={ω(v)∩H |v ∈B1},则对任意v ∈B1,因L是嵌入子背景,故存在sv ∈N使ω1(sv)=ω(v)∩H.作B2={sv |v ∈B1}⊆N,则B1={ω1(s)|s ∈B2}.由∪B ⊇H知∪B1==H,故B1是H在L中的AE-覆盖.

断言B1是A1的加细.事实上,任取ω1(s)∈B1,存在v ∈B1使ω1(s)=ω(v)∩H,这时ω(v)∈B.由B为A的加细知,存在u ∈B使ω(v)⊆ω(u),这时ω1(u)∈A1,从而ω1(s)=ω(v)∩H ⊆ω(u)∩H=ω1(u),这说明B1是A1的加细.

下证B1是H在L中的AE-局部有限集族.对于每一h ∈H,因B是H在K中的AE-局部有限覆盖,故存在v ∈V,使h ∈ω(v)且ω(v)仅与B中有限个成员相交不空,从而ω(v)∩H仅与B1中有限个成员相交不空.因L是嵌入子背景,故存在n ∈N使ω(v)∩H=ω1(n).这时h ∈ω1(n)且ω1(n)只与B1中有限个成员相交不空,这说明B1是H在L中的AE-局部有限集族.

综上所证,可知L是AE-仿紧背景.

推论4.1设(X,T)是拓扑空间,Y ⊆X.若由X中的开集构成的Y的每一覆盖A,总存在由X中开集构成的Y的局部有限覆盖B且加细A,则Y作为子空间是仿紧空间.

证记TY为子空间Y的拓扑.由子空间拓扑的定义知,L∈=(Y,TY,∈)为K∈=(X,T,∈)的嵌入子背景.因对任意的U ∈T,有ω(U)=U,故L∈满足命题4.1的条件,于是L∈为AE-仿紧背景,从而由命题3.1得Y作为子空间是仿紧空间.

定义4.1[7]设K=(U,V,R)是背景,称K的子背景L=(H,N,R ∩(H×N))是闭子背景,若存在有限集F ⊆V使H=U −ω(F).

文[7]给出了AE-紧致性关于闭子背景是遗传的结论.关于AE-仿紧性,有如下结论.

定理4.2设K=(U,V,R)是AE-仿紧背景,L=(H,N,R ∩(H ×N))是K的嵌入子背景,且H=U −ω(f),其中f ∈V.则L也是AE-仿紧背景.

证设B ⊆N及A={ω1(v)=ω(v)∩H |v ∈B}满足H ⊆∪A.令A ′={ω(v)|v ∈B},显然H ⊆∪A ′.令A ∗=A ′∪{ω(f)},则U ⊆∪A ∗.由于K是AE-仿紧的,故存在U的在K中的AE-局部有限覆盖B1={ω(v)| v ∈B1}是A ∗的加细,其中B1⊆V.记B2={ω(v)∩H |v ∈B1}−{∅},B2={v ∈B1| ω(v)∩H/=∅}.因L是嵌入子背景,故对任意v ∈B2,存在sv ∈N使ω(v)∩H=ω1(sv).作={sv |v ∈B2}⊆N,则B2={ω1(s)|s ∈},即B2是由L的某些非空属性外延组成的集族.因B1是U的AE-覆盖,故于是B2是H的在L中的一个AE-覆盖.

断言B2加细A.事实上,对任意v ∈B2,有ω(v)∈B1和ω(v)∩H ∈B2,由B1是A ∗的加细知,存在ω(n)∈A ∗=A ′ ∪{ω(f)},使ω(v)⊆ω(n),于是ω(v)∩H ⊆ω(n)∩H=ω1(n).因ω(v)∩H/=∅,故ω(v)⊈ω(f),从而ω(n)∈A ′,ω1(n)∈A,于是B2也是A的一个加细.

下证B2是H的在L中的一个AE-局部有限集族.由B1是U的在K中的AE-局部有限集族知,∀h ∈H ⊆U,∃v ∈V,使h ∈ω(v),且ω(v)仅与B1中有限个成员相交不空.从而ω(v)∩H仅与B2中有限个成员相交不空.因L是嵌入子背景,故存在n ∈N使ω(v)∩H=ω1(n).这时有h ∈ω1(n)且ω1(n)与B2中有限个成员相交不空.这说明B2是H的在L中的AE-局部有限集族.

综上所证,可知L是AE-仿紧背景.

推论4.1[11-12]若(X,T)是仿紧拓扑空间,(Y,TY)是X的闭子空间,则Y是仿紧的.

证由子空间拓扑的定义知,L∈=(Y,TY,∈)为K∈=(X,T,∈)的嵌入子背景.因Y是X的闭子空间,故存在G ∈T,使Y=X −G=X −ω(G).由定理4.2和命题3.1知L∈是AE-仿紧的,从而Y是仿紧的.

§5 形式背景范畴中乘积对象的AE-仿紧性

本节受文献[13]的启发考虑形式背景范畴的有限乘积对象的表示及其AE-仿紧性,所用到的范畴论知识来自文献[14].

命题5.1以形式背景为对象,以信息态射为态射可形成一个范畴,称为形式背景范畴,记为FCC.

证设(f1,g1)是从K1=(U1,V1,R1)到K2=(U2,V2,R2)的信息态射,(f2,g2) 是从K2=(U2,V2,R2)到K3=(U3,V3,R3)的信息态射.定义信息态射的复合(f2,g2)◦(f1,g1)=(f2◦f1,g1◦g2),则可直接验证关于该复合,形式背景为对象,信息态射为态射形成一个范畴.

定理5.1设K1=(U1,V1,R1),K2=(U2,V2,R2)是两个形式背景,它们在形式背景范畴FCC中的乘积对象可表示为K=(U1× U2,V12,∇),其中U1× U2为U1,U2的笛卡尔积,V12是V1,V2的无交并,关系∇⊆(U1×U2)×(V12)定义为：∀(u1,u2)∈U1×U2,v1∈V1,v2∈V2,(u1,u2)∇v1⇔u1R1v1,(u1,u2)∇v2⇔u2R2v2.

证设pi:U1× U2→Ui是投射使得pi(u1,u2)=ui ∈Ui(i=1,2).又设qi:Vi →V12为含入映射使得qi(vi)=vi ∈Vi ⊆V12(i=1,2).断言(p1,q1)为K到K1的信息态射,(p2,q2)为K到K2的信息态射.事实上,对(u1,u2)∈U1×U2,v1∈V1,由关系∇和q1的定义可得

这说明(p1,q1)为K到K1的信息态射.同理,(p2,q2)为K到K2的信息态射.

对任一给定的形式背景L=(U,V,R)及信息态射(f1,g1) :L→K1和(f2,g2) :L→K2需证明存在唯一的信息态射(f,g):L→K使(p1,q1)◦(f,g)=(f1,g1)和(p2,q2)◦(f,g)=(f2,g2).

存在性作f:U →U1× U2使∀u ∈U,f(u)=(f1(u),f2(u)),则p1◦f(u)=f1(u),p2◦f(u)=f2(u),由u的任意性知f1=p1◦f1,f2=p2◦f2.作g:V12→V,使∀v1∈V1⊆V12,g(v1)=g1(v1),∀v2∈V2⊆V12,g(v2)=g2(v2).因q1:V1→V12是含入映射,故g(q1(v1))=g(v1)=g1(v1),由v1的任意性知g ◦q1=g1,同理g ◦q2=g2.从而有

断言(f,g)是从L到K的信息态射,事实上,对u ∈U,v1∈V1⊆V1×V2,v2∈V2⊆V1×V2,有f(u)∇v1⇔(f1(u),f2(u))∇v1⇔f1(u)R1v1.又由(f1,g1)为L到K1的信息态射知f1(u)R1v1⇔uRg1(v1).因g1(v1)=g(v1),故f(u)∇v1⇔uRg(v1),同理有f(u)∇v2⇔uRg(v2).这说明(f,g)是从L到K信息态射.

唯一性假设另有从L到K的信息态射(f′,g′)使(p1,q1)◦(f′,g′)=(f1,g1),(p2,q2)◦(f′,g′)=(f2,g2).则对任意u ∈U,v1∈V1⊆V1×V2,v2∈V2⊆V1×V2,有

由u的任意性知f=f′.又易见

同理g(v2)=g′(v2).由v1,v2的任意性知g=g′.从而满足条件的信息态射是唯一的.

综上所证,定理中给出的K=(U1×U2,V12,∇)即为K1,K2在范畴FCC中的乘积对象.

在拓扑空间范畴中,紧致空间与仿紧空间的的乘积仍是仿紧空间,两个仿紧空间的乘积不必仿紧.但在形式背景范畴FCC中有如下更强的结论.

定理5.2在形式背景范畴FCC中,两个AE-仿紧背景的乘积对象仍是AE-仿紧背景.

下面证明B是U1×U2的AE-局部有限集族.对任意(u1,u2)∈U1×U2,由C是U2的AE-局部有限覆盖知,存在v2∈V2使u2∈ω2(v2)且ω2(v2)仅与C中有限个成员相交,这时(u1,u2)∈ω(v2)=U1× ω2(v2).因∀ω(c)=U1× ω2(c)∈B有ω(v2)∩ω(c)=U1×(ω2(v2)∩ω2(c)),故由ω2(c)∈C且ω2(v2)仅与C中有限个成员相交,知ω(v2)仅与B中有限个成员相交,这说明B是U1×U2的AE-局部有限集族.

综上所证,可知K为AE-仿紧背景.

推论5.1范畴FCC中,AE-紧致背景与AE-仿紧背景的乘积对象仍是AE-仿紧背景.

§6 结论

本文利用拓扑学的思想定义了形式背景的AE-仿紧性,给出了AE-仿紧背景的充分条件,研究了AE-仿紧背景的若干性质.证明了AE-仿紧性被适当的信息态射所保持,对一类特殊闭的嵌入子背景是遗传的.在以形式背景为对象信息态射为态射的范畴FCC中,给出了两个形式背景乘积对象的表示,证明了两个AE-仿紧背景的乘积对象仍是AE-仿紧的.这些结果说明本文定义的AE-仿紧背景是合理的有意义的,从而拓宽了形式概念分析的理论和拓扑学的应用范围.