对数恒等式在幂指函数极限中的应用对数恒等式在幂指函数极限中的应用

◎姚秀凤 孔祥铭 王 瑜

(北京电子科技职业学院，北京 100176)

极限是微积分理论中重要的概念.充分理解极限概念能够有效求解较复杂函数的极限问题，也是开启微积分学习的必备能力.学生从初等数学定量计算过渡到高等数学变化趋势的分析，会出现一些概念、性质及运算法则上的混淆现象.尤其是遇到较为复杂的运算——求幂指函数的极限时，由于题目的复杂性，常需要综合利用所学的等价无穷小、两个重要极限、洛必达法则等极限方法进行求解，而这也导致学生在解题过程中经常出现一些错误.

下面这道题目是学生在学习过程中遇到的一个相对复杂的含有幂指函数的极限问题.学生由于对第二重要极限、等价无穷小等知识的理解不准确，对解题方法综合应用不熟练，常出现错误的解题思路.学生的解题过程如下.

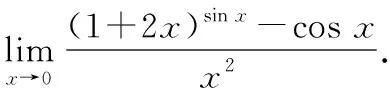
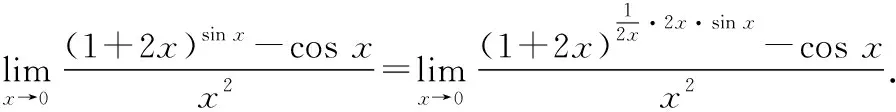
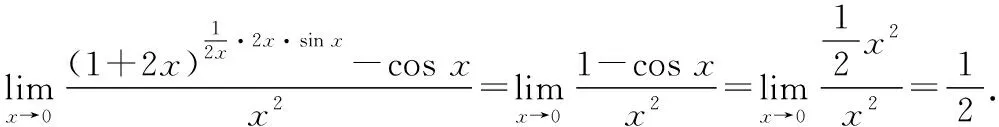
上述解题过程使用了第二重要极限和等价无穷小的知识.

一、第二重要极限

在教学过程中，我们需要引导学生分析公式中的重点,在自变量x→∞时:(1)函数为幂指函数形式；(2)底为1加无穷小(1+o)，指数为无穷大(∞)；(3)底中无穷小与指数上的无穷大必须互为倒数，同时满足这三个条件才能应用第二重要极限的结论.

学生在遇到题目时需要先对题目进行分析，分析是否满足相关条件，只有满足相关条件，才能应用相关结论，这也就是解决数学问题时所谓的“无条件不结论”.为了便于第二重要极限的应用，我们推导出下面的结论作为第二重要极限的知识拓展.

拓展后的公式也必须满足上述三个条件：(1)函数为幂指函数形式；(2)底为1加无穷小(1+o)，指数为无穷大(∞)；(3)底中无穷小与指数上的无穷大互为倒数.这是后续解决相关类型极限问题时要重点注意的.

二、等价无穷小

无穷小是极限为0的变量(函数)，记作ο.无穷小既不是很小的常数，也不可以随意用常数“0”来替换.在做无穷小的替换时，一定要准确理解无穷小的概念，在符合条件时才可进行替换.在解题时可以直接应用经过理论推导的等价无穷小的替代公式，这对简化解题过程将起到事半功倍的作用.下面列举几个常用的等价无穷小.

当x→0时，ex-1～x,ln(1+x)～x，推广可得：

当u(x)→0时，eu(x)-1～u(x)，

(1)

当u(x)→0时，ln[1+u(x)]～u(x).

(2)

三、错误解题思路解析

(一)混淆或忽略了第二重要极限的适用性

第二重要极限适用于1∞型未定式极限，即：

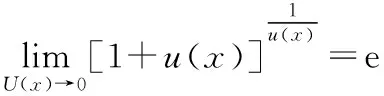
对于第二重要极限的应用，常用的变形是对幂指函数的指数部分进行简单的线性运算，而不是学生解题过程中对指数进行复杂化的非线性运算.

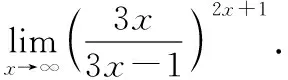
(二)对无穷小的“等价性”理解不准确

出现这些错误是因为学生对概念的理解不充分，对公式的记忆和运用不准确，对知识的掌握不扎实，运用公式不灵活，并且在实际求解中未形成应用对数恒等式进行简化运算的意识.下面我们以自然对数恒等式为载体，通过具体的例题讨论对数恒等式在求解幂指函数极限方面的应用，以帮助学生提高解决此类问题的能力.

四、对数恒等式在幂指函数变形上的应用

(一)对数恒等式及对数运算法则

(1)alogaN=N，其中，a>0且a≠1，N>0.

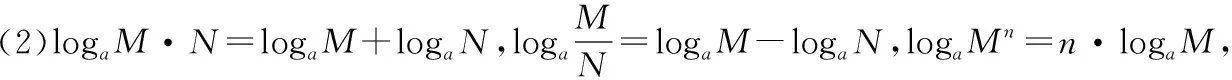
(二)幂指函数的恒等变形

对数恒等式是中学数学中的重要概念，自然对数恒等式eln N=N在高等数学中的应用也极为广泛，利用上面的恒等变形和对数运算法则能够将幂指函数由复合形式变形为积或商的形式，从而简化幂指函数的运算过程.有如下的推广应用：

u(x)=eln u(x)，

(3)

u(x)v(x)=eln u(x)v(x)=ev(x)·ln u(x).

(4)

例如，利用公式(4)和对数运算法则，可得：

(1+2x)sin x=eln(1+2x)sin x=esin x·ln(1+2x)，

(三)含有幂指函数的复合函数极限运算

在(4)式中，对幂指函数进行变形u(x)v(x)=eln u(x)v(x)=ev(x)·ln u(x)，能够得到以e为底的复合函数ev(x)·ln u(x).

由复合函数的极限运算法则，在自变量x的某种趋向下，若limv(x)·lnu(x)为有限常数，则：

lim ev(x)·ln u(x)=elim v(x)·ln u(x).

(5)

五、对数恒等式在幂指函数极限中的综合应用

在解决含有幂指函数的极限题目时，在第二重要极限不能使用或不便于直接使用的情况下，通常会用对数恒等式对其进行变形，在变形的过程中，利用对数的运算法则、等价无穷小及洛必达法则等其他极限方法求出正确的解.

(一)对数恒等式与洛必达法则在幂指函数极限中的综合应用

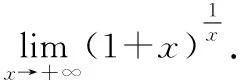
解这是∞0型未定式，不能使用第二重要极限.

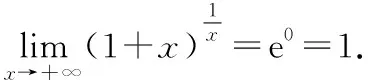
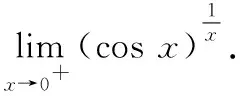
解这道题目虽然是1∞型未定式，但不符合第二重要极限的三个条件要求.

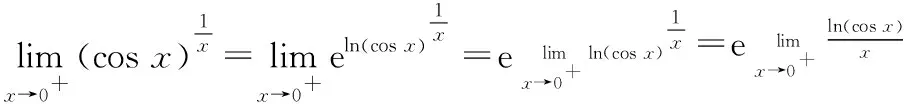
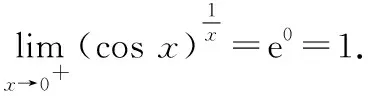
(二)对数恒等式与等价无穷小在幂指函数极限中的综合应用

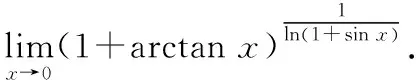
解这是1∞型未定式，无法直接套用第二重要极限，需先进行适当变形.

(1)应用对数恒等式对其进行变形：

(2)应用公式(2)进行等价无穷小的替换：

当x→0时，ln(1+arctanx)～arctanx，ln(1+sinx)～sinx，

在有些题目中，幂指函数只是题目的一部分，对于整个题目来说，需在严密的理论支撑基础上对函数进行更多的数学恒等变形，使之简化成能够用对数恒等式及对数运算法则进行变形，并能运用等价无穷小进行替代的式子，再综合使用其他求极限的方法，使题目得到完美解决.

下面，我们在上述分析对数恒等式及其他极限方法的基础上给出前面例1的正确解答.

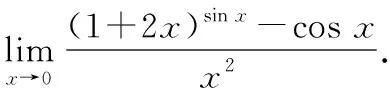
这个题目相对来说形式比较复杂，有三角函数、幂指函数和分数的形式，通过分析，在自变量趋于0时，只能够确定分母趋于0，分子(1+2x)sin x-cosx可看成“10-0”型未定式，无法进行适当的无穷小替换，需要先进行相应的恒等变形.

解(1)应用对数恒等式进行幂指函数的变形：

(1+2x)sin x=eln(1+2x)sin x=esin x·ln(1+2x),

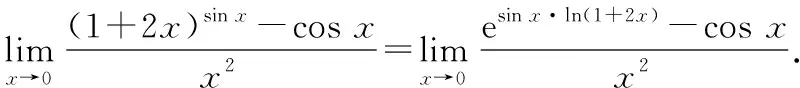
(2)对上式进行“加减项”的适当变形，可构造等价无穷小：

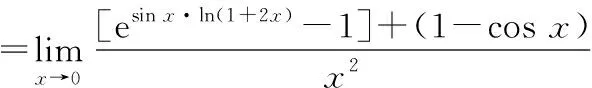
(3)进行等价无穷小的替换：

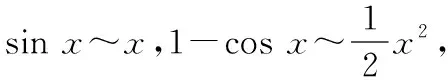
应用公式(1)和(2)，可得ln(1+2x)～2x和esin x·ln(1+2x)-1～sinx·ln(1+2x)，

即esin x·ln(1+2x)-1～sinx·2x～2x2.

(三)复合函数极限的存在性

上面的几道含有幂指函数的极限题目或因幂指函数的复杂性，或因不是1∞型未定式，而不能使用第二重要极限，故必须对幂指函数进行对数恒等变形，再运用极限的其他方法完成求解.在求解过程中，还需要注意以e为底的复合函数极限的存在性，以免出现错用结论的现象.下面我们看一道简单例题.

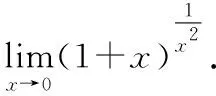
本题的正确解法如下.

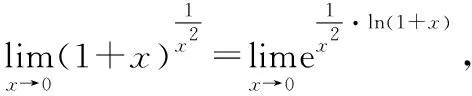
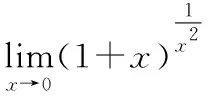
下面，为了更准确地理解结论(5)的适用性，帮助学生拓展解题思路，我们试着抛开第二重要极限，利用复合函数极限存在的结论对前边的例题2进行求解.

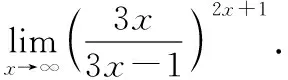
(1)应用对数恒等式将幂指函数变成函数乘积的形式：

六、结 语

通过以上分析和过程详解，我们可以总结出，对于极限题目中含有幂指函数的形式，既要考虑其是否符合第二重要极限的条件，也要积极寻找其他解题方法.如果符合条件，则考虑利用第二重要极限公式解决该题目是否便于求出答案；符合条件但不便于直接使用第二重要极限的题目，可先对其进行对数恒等式的变形，再综合运用相关知识进行求解；如果不符合条件，需先对其进行对数的恒等变形，将幂指函数变形成积或商的简单函数形式，再结合其他极限求解理论和方法，使复杂的幂指函数极限得到便捷、完美的求解.对于学生而言，学习更多的理论、法则不是为了机械套用，而是要学会思考，学会创新，不断地把所学知识融会贯通，从而解放思想，创新思维，在寻找适合的解题思路和方法的过程中培养缜密的逻辑思维能力，提高解决问题的应用能力.