“研题”助推教师专业成长“研题”助推教师专业成长

◎钱 江 庄美珊

(1.深圳市宝安中学，广东 深圳 518000；2.深圳市民治中学，广东 深圳 518000)

波利亚曾说过：“掌握数学就意味着要善于解题.”而要做到“善于解题”需要长期的训练——研题.“研”乃石开也，即把石头撬开，不仅需要勇气与智慧，更需要高屋建瓴、谋全局的意识．教师通过解题研究(简称“研题”)挖掘题目蕴含的数学思想方法和一般规律，透过现象认识本质，可帮助学生走出题海，提高学习效率，减轻学生的学习负担．研题既是高中数学教师必备的素养与能力，教学研究的重要组成部分，也是促进教师专业成长的有效途径．那么何为研题？研哪些题？又该怎样开展研题?

一、何为研题

研题，是在正确解题的基础上对题目进行反思，挖掘题目的内涵与潜在价值.也就是教师对题目进行更深入的研究分析，寻找命题规律，帮助学生更好地应对考试，从教师的角度分析题目的设计意图和考查方向，并最终进行系统整理与拓展的过程.

二、研何题

(一)研课本题明题源

教师在研究高考真题时会发现很多题目“似曾相识”，总能找到教材例题、习题的影子，是教材中例题、习题的再现与重组或变式与拓展.高考试题“源于课本”，这是由高考的性质决定的.教师要善于寻找高考试题的课本生长点和命题背景，探究题源，挖掘命题的“题根”，达到由例及类、触类旁通的目的，这对提高学生数学解题能力、培养思维品质、落实核心素养、改进学生学习方法、减轻学生学习负担都是大有裨益的.

(二)研高考真题观趋势

研究历年高考真题的意义绝不在于“做题”本身，而在于通过高考真题探索命题趋势、规律，实现以下目标：①理解以素养为导向、能力为重的命题原则；②梳理高考真题的通性通法，拓展一般性规律；③把握“重视数学本质，突出理性思维、数学应用、数学探究、数学文化引领，突出对关键能力的考查”的命题方向；④完善知识体系，运用高考真题体会知识和考点之间的内在关系，提升课堂解题教学的指导性、针对性和高效性；⑤学习高考题的命题方法，提升自己的命题能力.

(三)研模拟习题学变式

随着新课改的深入，越来越多的竞赛试题、省地市模拟题等呈现出回归教材及历年高考真题的趋势.特别地，一些试题的“题根”直接来源于历届各省高考真题，是利用变形、转化、深入、创新、拓展应用等手段加以合理改编得到的.教师对各地市的模拟题进行研究，除了可以进一步提升自己的解题能力，还能有效提升命题能力.

三、如何研题

研题是一个相当复杂、内容相当丰富的工作.为了更好地促进学生在数学学习过程中的全面发展，教师通常需要针对题目的解题方法进行变式研究.关于研题的具体实施步骤，课题组总结出以下四个方面.

(一)研“解”

教师研题的基础是解题，即重视解题方法对学生思维能力的培养.教师通过探究一道题目的不同解法，可培养学生的创造性思维能力和抽象思考能力，加强学生的解题实力；可通过多题一解，加大学生的思维深度，学会由表及里地分析问题，抓住问题的本质；可通过解法将一道试题解法的多样性和不同解法的差异性挖掘出来，培养学生的思维品质和数学素养.教师研题时要根据学生能力、知识、思想方法的差异性从多角度进行思考，力求举一反三，通过探求不同的解法向解一类题、一组题的方向发展.

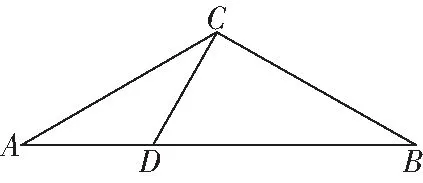
图1

该题是在多个三角形中，利用正、余弦定理解三角形的一道经典题型，渗透了数形结合、转化与化归、方程等思想.本题主要有以下几种解题思路.

思路一：利用面积关系构建桥梁.

在△ACD中,

AD2=AC2+CD2-2AC·CDcos∠ACD

∴AD=5.

思路二：利用角互补构建桥梁.

在△ABC中，∵BD=2AD，设AD=x(x>0)，则BD=2x.

在△BCD中，∵CD⊥BC，CD=5，BD=2x，

∵∠CDB+∠ADC=π，∴cos∠ADC=-cos∠CDB，

思路三：利用公共角构建桥梁.

在△ABC中，∵BD=2AD，设AD=x(x>0)，则BD=2x.

在△BCD中，∵CD⊥BC，CD=5，BD=2x，

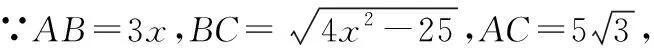
由余弦定理,得

解得x=5，∴AD的长为5.

思路四：利用平面几何知识添加平行线.

图2

过D作DE//AC,

在Rt△DCE中，

以下同解法1.

以上几种方法是解多个三角形问题的常见解法，通法是利用多个三角形的公共边、相同角、互补角、面积等构造方程.在同一数学情境中，不同解题思路、程序的设定可体现解题人对于具体数学问题特征的把握，以及对内涵的挖掘.一题多解不是解题追求的目标，而是要提炼解决问题的通性、通法，形成数学方法和思想，促进学生数学素养的提高.

(二)研“规”

一个好的题目一定是入口宽、出口窄、解法多样的，但无论哪一种方法，最后又能回归到通性、通法上来.我们应该依托试题，在深入研究多种解法的基础上探求其内在规律，理清试题内在的本质属性.我们还应进一步思考问题背后的本质是怎样的，解题方法蕴含着怎样的通性、通法和数学思想，是否存在更一般的规律，为什么会有这样的规律.

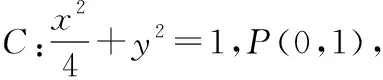
此题为2017年全国Ⅰ卷理科20题的第(2)问，过椭圆短轴顶点P,作两条斜率和为定值-1的两条直线与椭圆相交，证明它们的交点弦恒过定点，属于圆锥曲线的热点、难点问题——定值定点问题.

教师可采用从特殊到一般的合情推理的方法进行类比，引导学生将条件进行变式拓展，探索得到一般性推论，从而揭示问题的本质.教师可引导学生大胆猜想：此题定点P为椭圆短轴的顶点，点P是否可以为椭圆上任意定点？两条直线斜率之和为-1如果改为斜率之和为1,2，…，甚至是任意常数，相交弦所在直线都一定过定点吗？还有其他情况吗？斜率之和为定值是否能改成斜率之积为定值，这时直线仍过定点吗？几何载体能否从椭圆类比推广到双曲线、抛物线？经过严格的证明，对此类定点定值问题可以归纳出一般性的结论.

推论一：

在圆锥曲线中，曲线上一定点P(x0,y0)(非顶点)与曲线上的两动点E，F满足直线PE与直线PF的斜率互为相反数，则直线EF的斜率为定值.

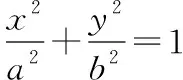
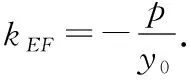
推论二：

若曲线C:mx2+ny2=1(m,n≠0)，P(x0,y0)为曲线C上一点，不过点P的直线l与曲线C交于E,F两点，且直线PE,PF的斜率存在.

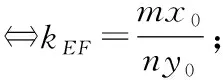
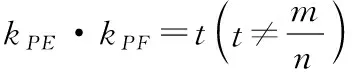
本题可以拓展为典型的“手电筒”模型，即在圆锥曲线上任取一点P,只要限定直线AP，BP斜率的条件，如斜率和为定值、斜率之积为定值，甚至斜率之差为定值，动直线AB依然会过定点或者斜率为定值(因为三条直线形似手电筒，故称手电筒模型).联想这几年的高考题，不少题型都是以圆锥曲线的几何性质为背景来命题的.

图3

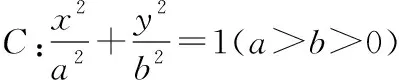
(1)求C的方程；

(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

本题第(2)问因条件多，学生感觉无从下手.教师可引导学生从结论出发逆向思考，若存在定点Q，使得|DQ|为定值，那么动点D的轨迹是以Q为圆心的圆.条件“点M，N在C上，且AM⊥AN”可转化为椭圆上两动点M，N,与椭圆上的定点A的斜率总满足kAM·kAN=-1,由“手电筒模型”知，动直线MN必过一定点E.再由条件AD⊥MN推导出动点D在以AE为直径的圆上，定点Q即是A，E的中点.所以，此题可转化为一个常见题型：由kAM·kAN=-1,求出动直线MN必过定点E.

图4

推论三：切点弦过定点问题，若P(x,y)在圆锥曲线外的一条定直线Ax+By+C=0上移动，那么过动点P的所有切点弦所在直线过定点.

以上两道题的本质是推论二的特例，通过命题专家的精心“打扮”而使学生不识“真面目”，这里因篇幅所限，解答过程略.

茫茫题海，问解何处觅，真题探规，尽览众山小.高考复习备考要重视对高考真题的研究，教师要引导学生抓住试题特征，把握问题本质，发现试题的共性，对同根、同源、同宗问题进行归纳和拓展，达到解一道题会一类题，融通相关问题，从真题中找到高考的变化趋势，从同类试题中找到变化规律，收到举一反三的效果，实现高效复习.

(三)研“源”

对于一道经典试题，教师要善于研究问题出处，探寻题根，并深刻挖掘基于题根的命题思路.这种基于“问题从哪里来的，怎样演变的，命题者的命题思路和方法是什么”的思考，以及力求站在命题者的视角审视问题，求本归真研究“题源”的方法，更有利于提升学生的数学学科素养.

1.真题再现

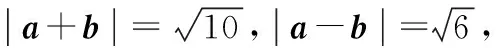
A.1 B.2 C.3 D.5

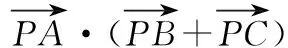
2.寻根溯源

上述两个问题的背景源于普通高中课程标准试验教科书数学必修4A版第108页习题2.4中的A组第3题.

题目：已知|a|=2,|b|=5,a·b=-3，求|a+b|,|a-b|.

证明：∵(a+b)2=a2+2a·b+b2, ①

(a-b)2=a2-2a·b+b2, ②

3.本质挖掘

图5

式③就是著名的“极化恒等式”，也叫“广义平方差”公式.

图6

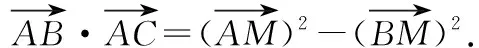
极化恒等式的作用在于把两个向量的数量积转化为这两个向量的“和向量”与“差向量”，因此当两个向量的“和向量”或“差向量”为定向量时，可以用极化恒等式进行转化.此恒等式的精妙之处在于建立了向量与几何长度(数量)之间的桥梁，实现了向量与几何、代数的巧妙结合，具有化动为定、化曲为直的作用.

图7

例2略解：如图7，取BC中点D,取AD中点E，

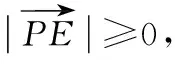
4.拓展延伸

图8

分析：此题的难点为A，B，M三点均为动点,若采用常规的设线AB方程和动点M坐标，再转化为函数问题，计算会非常烦琐.

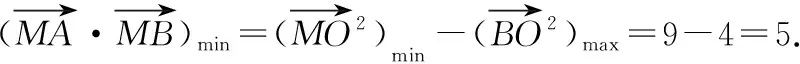
(四)研“变”

变式教学是常用、有效的教学方法之一.在解题教学过程中，教师需要将试题进行变形、引申、推广或拓展，形成题组进行教学.这样可以更好地发挥题组的整体作用，帮助学生形成更好的认知结构，促进学生对数学本质的理解与领悟，提升学生分析与解决问题的能力.变式可以沿着由浅入深的路径，体现学生学习过程的循序性与层次性；也可以沿着“形似但质异”的思路，体现数学本质，并训练学生思维的灵活性；也可以沿着“异题同解”的思路举一反三，强化通性、通法与解题规律.常用的变式方法包括特殊化、一般化、变换背景、改变设问方式等，可改造问题的条件或结论，也可同时改变问题的条件与结论.

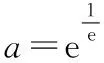
变式1：已知a>0且a≠1，若y=ax与y=logax的图像恰有一个公共点，则实数a的取值范围为________.

变式2:(深圳市2021年高二年级期末全市统考)设k>0，若存在正实数x，使得不等式log27x-k·3kx-1≥0成立，则k的最大值为( ).

此题为一道常规的含参不等式有解求参数范围问题，但全市平均分仅0.3分.不等式同时含对数和指数且参数k不易分离是此题的难点.大部分学生按照小题大做的方法，直接转化为函数求导，采用分类讨论方法求最值，但导函数为含参的超越函数，难以求解.问题的突破口应该从不等式结构入手，突破形式困扰，挖掘本质，方能柳暗花明.

令a=3k，则问题转化为logax≥ax有解，求a范围，此时解题明显简单了.

因为y=logax与y=ax互为反函数，则可转化为直线y=x与y=logax或y=ax有交点.

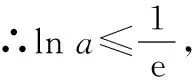
四、结束语

美国著名数学家波利亚曾说：“解题的价值不是答案的本身，而在于弄清‘是怎么想到这个解法’‘是什么促使你这样想这样做的’.”解题过程是一个思维过程，是把知识与问题联系起来思考、分析、探索的过程.波利亚认为，“对你自己提出问题是解决问题的开始”“当你有目的向自己提出问题时，它就变成了你自己的问题了”.在学习数学中，我们就是要教会学生如何思考问题，如何将问题深化，如何挖掘数学问题的本质，通过研解、研源、研规、研变等方式深入研究解题教学，帮助学生从浩瀚的题海中解脱出来，避免刷题带来的繁重负担，发展学生的核心素养，提高学生解决问题的能力.