别样辅助线——辅助圆在解题中的妙用

郑红燕

(新疆若羌36团中学 新疆 若羌 841800)

添加辅助线是几何题帮助解决问题的常用方法，合适恰当的辅助线使所解决的问题和已知条件之间搭起桥梁，把分散的条件集中起来，可以让题目解题方向清晰、解题快捷。通常添加辅助线作的是直线，中考复习中发现有一类题偏偏添加辅助线“圆”能使题目柳暗花明，解题思路一目了然，使题目由难变易，轻松解决，并且培养学生的观察能力，所以在中考第二轮复习中笔者尝试做了一个构造辅助圆的微专题，期待对学生解题有所启发，解题思路开阔一点，培养数学发散思维。

因此制定微专题教学目标如下：

1.熟悉圆的定义、相关性质和定理。

2.灵活运用条件构造辅助圆，分析题目解决问题。

为了衔接紧密，先复习圆的相关知识。

复习：

1.圆的“集合”定义是什么？圆是所有到定点的距离等于定长的点的集合

2.圆周角定理及推论是什么？

同弧或等弧所对的圆周角相等；一条弧所对的圆周角它所对的圆心角的一半。

半圆(或直径)所对的圆周角是直角。

90°的圆周角所对的弦是直径。

在中考复习过程中经常遇到的情形大致可以分为以下几个类型可以作辅助圆解决问题：

一、当遇有“同一个端点出发的等长线段”时，通常以“这个端点为圆心，等线段长为半径”，构造辅助圆。

例1.如图1所示，在四边形ABCD中，AB=AC=AD，∠BAC=20°∠CAD=80°，则∠BDC=______度，∠DBC=______度。

图1

学生思考：什么条件让你想到可以构造圆，可以构造圆的依据是什么？

条件：同一个端点出发的几条等长线段。

依据：圆的定义。

回顾圆的定义：圆是所有到定点的距离等于定长的点的集合。

作法：当遇有“同一个端点出发的等长线段”时，通常以“这个端点为圆心，等线段长为半径”，构造辅助圆。

解：因为AB=AC=AD，所以点B、C、D可以构成以点A为圆心，AB为半径不共线三点共圆，

所以根据圆的相关性质得∠BDC=∠BAC=20°；∠DBC=∠CAD=80°。

练习1：如下图2，OA=OB=OC且∠ACB=30°，则∠AOB的大小是( )

A.40° B.50 C.60° D.70°

(分析：如右图3所示只需以点O为圆心OA为半径作圆，有圆的性质可得∠AOB=60°)

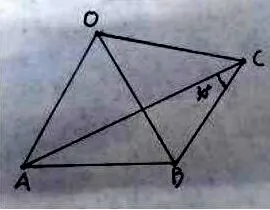
图2

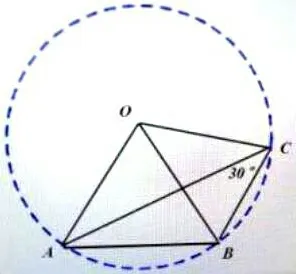
图3

练习2：如图4所示，四边形ABCD是平行四边形，

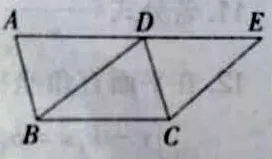
图4

图5

延长AD至点E，使DE=AD，连接BD。

(1)求证：四边形BCED是平行四边形。

分析第二问：这一问的方法较多，期中有一种借助圆来求BE，不用证菱形，方法简洁明了，不拖泥带水。解答如下：

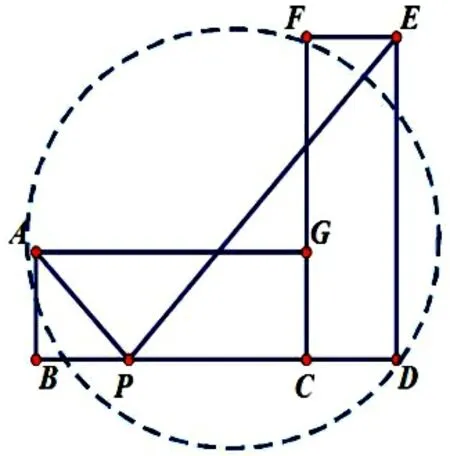
图6

二.当遇有“直角”时，通常以“斜边为直径”构造辅助圆。

例2.如图4，矩形ABCG的与矩形CDEF全等，并且AB=1，BC=3，点B、C、D在同一条直线上，∠APE的顶点P在线段BD上移动，使∠APE为直角的点P的个数是( )。

A．0 B．1 C．2 D．3

学生思考：什么条件让你想到可以构造圆，可以构造圆的依据是什么？

条件：直角。

依据：90°的圆周角所对的弦是直径。

作法：当遇有“直角”时，通常以“斜边为直径”构造辅助圆。

解：如图以AE为直径构造圆，与BD有两个交点，所以可得满足条件的点P有2个。(此题构造辅助圆使得题目直观形象，一目了然)。

例3.如图7，在等腰直角三角形ABC中，∠B=90°，D是AC的中点，过点D作DE⊥DF，交边AB于点E，边BC于点F，求证：DE=DF。

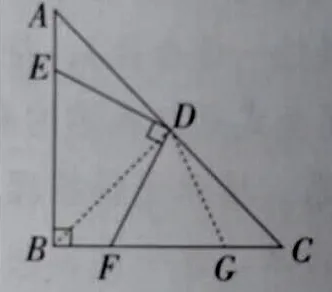
图7

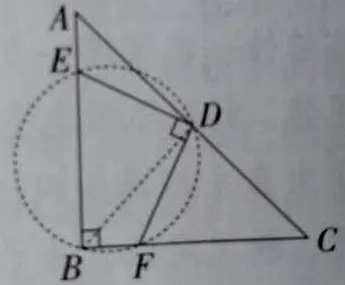
图8

分析：这道题有多种解法，其中有一种是构造全等三角形，并进行证明。还有一种如图8，已知∠ABC=90°，∠EDF=90°，从而想到可构造以EF为直径的圆，连接BD，则∠ABD=∠CBD=45°，所以ED=DF。

图9

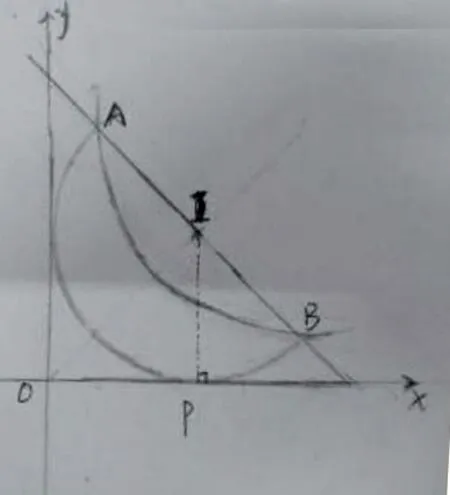
图10

取AB的中点为I，则IA=IB,因为∠APB=90°，由90°所对的弦是直径，以AB的中点I为圆心，AB的一半为半径作圆，又因为点P为x轴上的动点，点P与x轴有且只有一个交点，所以○I与x轴有且只有一个交点，即○I与x轴相切。

最值问题是中考经常考查的热点，有的问题我们通常利用垂线段最短、轴对称的知识解决，比如典型的将军饮马问题，折点P是使这两条线段之和最短的动点，动点在一条直线上，换句话说动点的轨迹是一条直线，其实有时动点轨迹可以改变，点P的轨迹也可以是一个圆。

有的问题中，很少直接告诉我们动点轨迹是圆，也很少画出圆，因此，结合题目各个条件，分析出动点轨迹是圆，达到“四两拨千斤”，化繁为简，事半功倍的效果。

根据点与圆的位置关系性质分析。

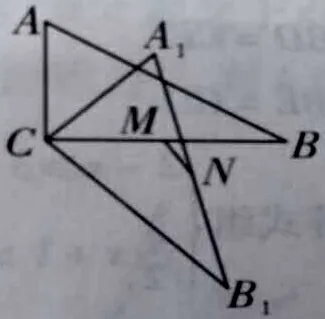
图11

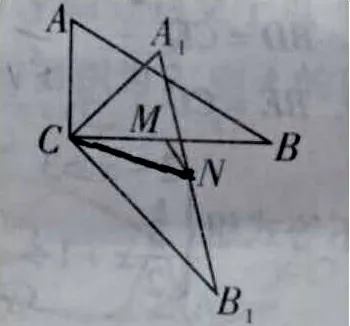
图12

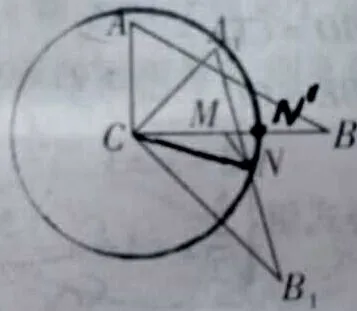
图13

三、(1)当遇有相同的角对的边是同一条线段时，通常把相同的角转化为圆周角构造圆，这条线段是圆中的弦。

即某条线段以及这条线段所对的角大小固定，则角的顶点在以AB为弦的圆弧上。

例6.如图14，BD、AC相交于点P，连接AB、BC、CD、DA,∠ADB=∠ACB。若AB=8，CD=4，DP=3，则AP的长为_______。

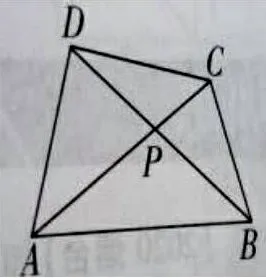
图14

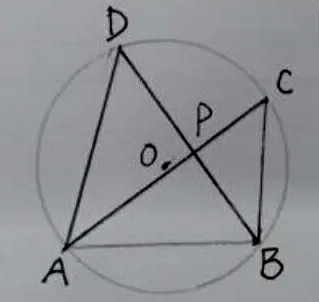
图15

学生思考：什么条件让你想到可以构造圆，可以构造圆的依据是什么？

条件： 两个相等的角所对的边是同一条线段。

依据：同弧或等弧所对的圆周角相等。

作法：当遇有“相同的角对的边是同一条线段”时，通常把“相同的角转化为圆周角”构造辅助圆。

解：∠ADB=∠ACB，且对的线段时同一条线段AB，则可以想到点A、B、C、D四点共圆，所以△DPC∽△APB，可知DP：AP=4:8=1:2,如图15，隐去线段CD，可以看出∠D=∠C，可知△DPA∽△CPB，DP：AP=1:2=3:AP,所以AP=6。

(2)当遇有动点对定线段所张的角为定值时，通常把张角转化为圆周角构造辅助圆。

例7.如图16，在平面直角坐标系中，已知点A(4，0)、B(﹣6，0)，点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为( )。

图16 图17

学生思考：什么条件让你想到可以构造圆，可以构造圆的依据是什么？

条件：动点对定线段所张的角为定值。

依据：不在同一直线上的三点确定一个圆；同弧或等弧所对的圆周角相等；

同弧所对的圆周角相等且等于这条弧所对的圆心角的一半。

作法：

当遇有动点对定线段所张的角为定值时，通常把张角转化为圆周角构造辅助圆。

练习：

如图18，点A与点B的坐标分别是(1,0)，(5,0)，点P是该直角坐标系内的一个动点。

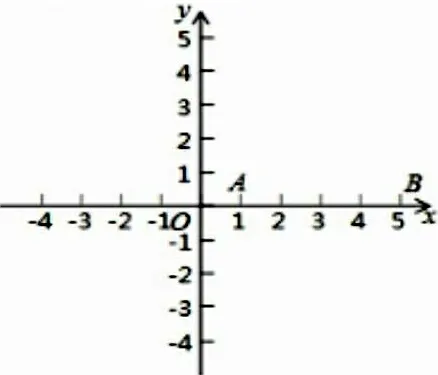
图18

(1)使∠APB=30°的点P有( )个；

(2)若点P在y轴上，且∠APB=30°，求满足条件的点P的坐标。

解答略。

总结：图中无圆，心中有圆。

以上研究的这几类问题，从表面上看似乎与圆无关，但如果我们能深入挖掘题目中的隐含条件，善于联想所学定理，巧妙地构造符合题意特征的辅助圆，再利用圆的有关性质来解决问题，往往能起到化隐为显、化难为易的解题效果。