正比例收获滞后Logistic单种群模型的稳定性分析

叶陆红

（安庆师范大学 数理学院，安徽 安庆 246133）

常微分方程可以反映事物的发展趋势，但事物的发展趋势不仅取决于当前状态，还取决于过去或未来时期的状态，因此描述这些现象的微分方程不是通常意义上的常微分方程，它既含有自变量t，还含有形如t-r(t)的带滞后的变元，其中r(t)称为偏差。上述方程通常被称为滞后偏差变量元素的微分方程[1-8]。

单种群生物模型是种群生态学发展最早的模型，尽管自然界中各个种群之间有关联，但若把考虑因素全部加到模型上，则模型太过复杂且不易研究其动力学性质。因此学者们大多是围绕单种群模型进行系统研究[1,6]，这对于研究物种的可持续发展具有重要的指导意义。1838年，Verhulst[8]在研究单组模型增长规律的过程中，由于资源有限，考虑到组内竞争等因素，构建了Logistic模型：

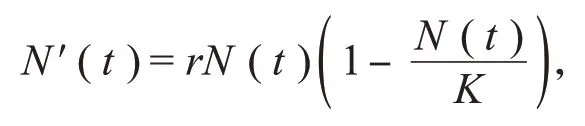
其中，N(t)是某种群在t时刻的密度，r是内秉增长率，r＞0，K是该种群地区的最大环境容纳量，K＞0。该模型考虑的是t时刻的种群增长速度仅依赖于t时刻的种群密度，但种群的再生繁衍有个时间过程，即种群密度在t时刻的变化速度不仅依赖于t时刻的种群密度，而且与过去种群的密度有关，故Hutchinson首次构造出具有时滞的Logistic模型[7]：

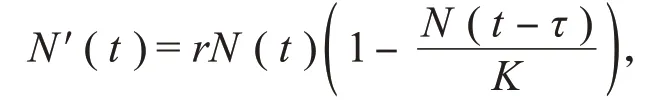
该模型可以更好地解释种群动力学行为。

考虑到种群的收获，本文研究正比例收获的滞后Logistic单种群生长模型：

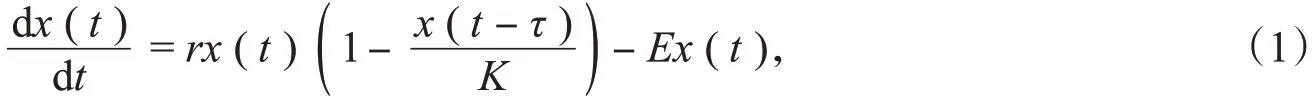
其中，x(t)表示在t时刻的种群密度，E表示收获系数，Ex(t)表示正比例收获，时滞τ表示种群成熟期，设r＞E＞0。本文将通过τ划分特征根分析法[1,4]，讨论方程（1）的特征根分布，进而得到稳定性结论，并通过数值模拟验证结论的正确性。

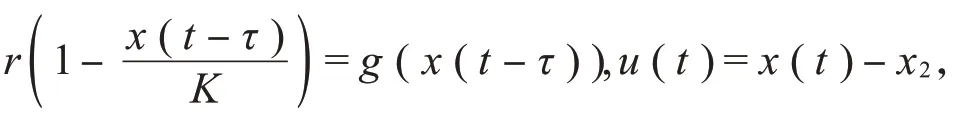
并将其代入式（1）得：

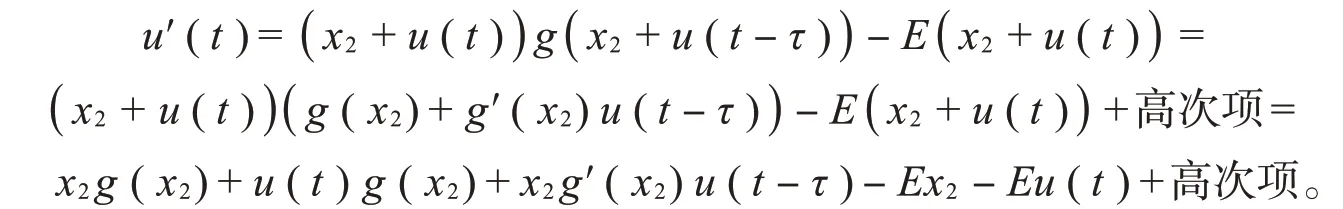
式（1）的线性化方程为

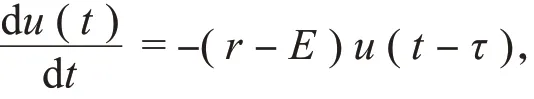
因此式（1）的特征方程为

下面分析式（1）的特征根情况。当τ=0时，得λ=E-r＜0，显然λ=0不是方程（2）特征根。若iω(ω＞0)为方程（2）的纯虚根，则代入方程（2）中，分离实部和虚部得：

将式（3）中方程两边平方后相加得：ω2-(r-E)2=0，即ω=r-E。由式（3）的第1个方程得：

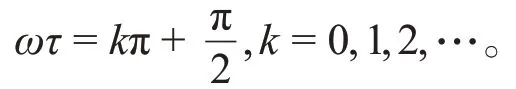
由式（3）的第2个方程得：

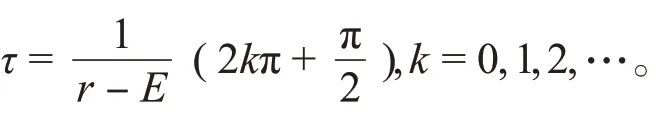
令

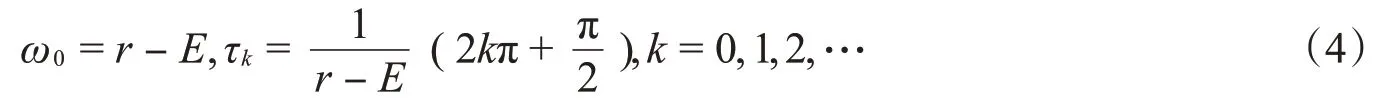
于是，对每个k≥0,(τk,ω0)是式（3）的一个解，即±iω0是方程（2）当τ=τk时的一对纯虚根。显然，当τ≠τk时，方程（2）没有纯虚根。

下面验证横截条件。令λ(τ)=α(τ)+iω(τ)是方程（2）满足α(τk)=0,ω(τk)=ω0的根。将λ(τ)代入方程（2）且对τ求导，注意到λ(τ)=-(r-E)e-λ(τ)τ，故

将τ=τk代入式（5）有：

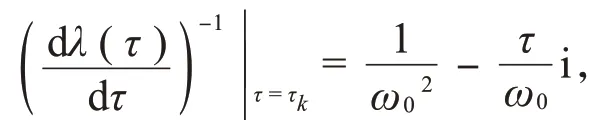
由sign(Re(a+ib))=sign(Re(a+ib)-1)知α′(τk)＞0。因此得到以下引理。

引理假设r＞E＞0，则存在一列{τk}k≥0，它们由（4）式定义，使得当τ∈[0,τ0)时，方程（2）的所有特征根都有严格的负实部；当τ=τk时，方程（2）有一对简单纯虚根±iω0；当τ∈(τk,τk+1]时，方程（2）恰有k+1对具有正实部的根。

分析：从参考文献[1]可知结论成立。如果±iω0不是单根，则有

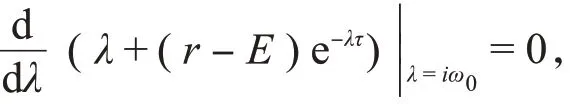
即ω0满足1-τ(r-E)[cosωτ-isinωτ]=0，分离其实部和虚部得：

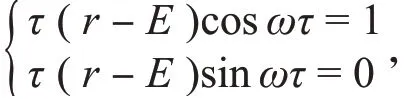
故tanωτ=0。又由式（3）知tanωτ=∞，矛盾，因此iω0是单根。

由引理可直接得到关于正平衡解x2的稳定性结论。

定理若r＞E＞0，则当τ∈[0,τ0)时，方程（1）的正平衡解x2是渐近稳定的；当τ＞τ0时，方程（1）的正平衡解x2是不稳定的；当τ=τk(k=0,1,2,…)时，方程（1）在x2处经历了Hopf分支。

下面给出一个数值模拟的例子以验证上述结论。对模型（1）取参数：r=0.2,K=2,E=0.1,τ=1，则在这组参数下有r＞E＞0，满足定理的第1个结论。由图1可看出模型（1）的正平衡解x(t)渐近稳定，其生物意义是：随着时间的延长，单种群规模最终会走向灭绝，因此时滞对物种的可持续性发展研究有指导意义。

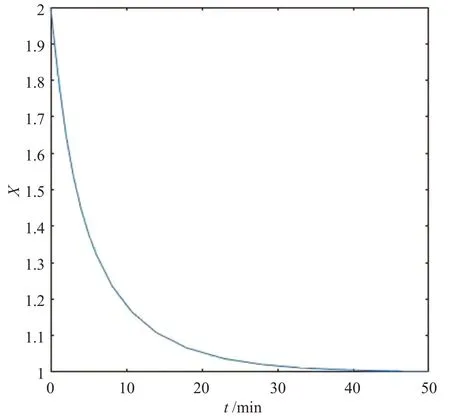
图1 模型（1）正平衡解渐近稳定示意图

注在用数学模型研究生态系统时，为了更好地掌握一般原理，有必要从模型的单种群开始研究。本文主要得到正比例收获滞后的单种群模型在时滞参数不同条件下，正平衡解渐近稳定、不稳定及发生Hopf分支情形，即得到时滞参数对模型平衡解稳定性的影响。后续工作可以对于平衡解的全局稳定性进行研究，或在线性收获下，讨论时滞作用对生物种群的平衡点稳定性的影响。