一种求解大规模CVRP的有效算法

饶 舜，张玉州

（安庆师范大学 计算机与信息学院，安徽 安庆 246133）

随着科技不断发展，人们生活半径也在不断扩张。为了更好地符合实际优化车辆路径规划，大规模带容量限制车辆路由问题（LSCVRP）逐渐成为车辆路由问题的研究热点。Li等为了应对LSCVRP实际需要，于2005年设计了生成大规模标准测试样例的方法，构造了包含12个测试样例的测试集（记为Li），客户数由先前的500增至1 200，成为近年来LSCVRP解决方法有效性验证的重要测试对象[1]。鉴于CVRP属于NP-hard，由问题知识或搜索结果作为启发信息而形成的启发式算法成为求解CVRP的主流方法[2-7]，其中邻域探索是发现更优解的一种有效途径[3,6-7]。

随着问题规模的增大，如何引导算法在更有效的解空间进行搜索成为处理大规模问题的关键。文献[1]、[8]均以LSCVRP为对象，进行了求解方法的设计，尤其是文献[1]生成了规模达1 200的标准测试集。然而，这些方法对如何降低问题搜索复杂性欠考虑。Kytöejoki等就LSCVRP提出了几种问题求解算法，并利用邻域搜索（NS）机制对现有解进行了局部探索，从而获取更优的问题解[3,8-9]。

Taillard针对问题结构的不同，设计了两种不同的基于分治（DC）策略的分解方法[10]，Reimann则依据客户的地理位置，将问题转换为若干较小的问题进行处理[11]。Feng于2015年提出了一种VRP与CARP求解方法的转换方法[12]。2017年，Tang提出了层次分解（HD）策略，并以虚拟任务的形式简化问题，设计了基于HD的大规模CARP求解算法（SAHiD），在更大规模上对CARP进行了求解，并显示了卓越的性能[13]。Zhang发现文献[13]以随意截断后的路径为聚类对象过于粗糙，提出了一种基于任务等级的路径切割方法（RCO）[14]并用于文献[13]的路径聚类，明显提高了算法的问题求解效果[14]。

鉴于SAHiD在大规模CARP上的良好问题处理能力，该研究尝试将层次分解（HD）策略引入至LSCVRP的求解，以变邻域搜索（VNS）对当前解进行局部搜索，结合Zhang提出的路径切割技术[14]，所设计的方法记为HD-VNS，并过对两个测试集、32个测试样进行计算。

1 问题描述及模型建立

LSCVRP与普通CVRP场景描述类似：区域内一仓库配套有车队，服务于一定范围内客户的所需物资配送。每辆车均由仓库出发，沿途对客户提供服务，最后返回仓库。车辆受最大载重量Q约束。目标为寻找最优的车辆路径，满足所有客户的配送要求，并使车辆的行驶距离最短（成本最低）。

模型相关符号定义：客户集C={ }c0,c1,c2,…,c n，n为客户数，每个客户c i(1≤i≤n)均存在一定的服务需求量di，c0为驻扎了m辆车的中心点，可被认为无服务需求的特殊客户；位于c0处的m辆车构成车队集合V(k∈V)，其中每辆车的最大负载量为Q，最长行驶距离为L；χki,j为二值变量，1表示车辆k(k=1,2,3,…,m)由客户ci行驶到客户c j(i≠j)，否则为0；γki为二值变量，1表示客户ci由车辆k服务，否则为0；δi,j为客户ci、cj之间的距离，采用欧氏距离计算形式。

基于上述符号定义，LSCVRP的数学模型描述如下，

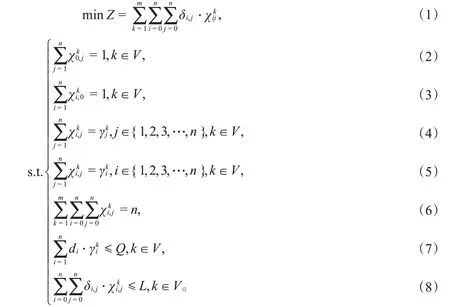
上述模型中，式（1）为问题的目标函数，即所有车辆完成服务的总行驶距离最小；式（2）和（3）分别表示车辆从中心点出发，完成服务后返回中心点；式（4）～（6）确保每个客户被服务有且仅有一次；式（7）和（8）确保车辆的最大载重约束条件以及最长行程距离。

2 算法设计

2.1 算法步骤

为了能够对大规模CVRP进行有效处理，该研究以SAHiD中的HD为问题聚类方法，采用类似于该算法的框架结构，并使用RCO对路径进行切割，以变邻域搜索（VNS）对解进行局部搜索。因为问题结构不同，如CARP中路径通常是由需求任务的边组成，而CVRP中路径是由客户节点组成，所以需要将SAHiD的任务转换为CVRP客户，且客户间采用欧式距离直接计算。基于HD分治算法的HD-VNS基本步骤如下。

步骤1设置最大迭代次数g、最大无进展迭代次数n；

步骤2生成初始解s；

步骤3初始化参数，迭代次数i=0，无进展迭代次数m=0；

步骤4构建临时变量s′，记录解s′=s；

步骤5使用文献[14]的路径切割方法RCO对s′的路径进行切割，得到路径集合R；

步骤6使用文献[13]的层次分解策略HD对R分解，获得一个包含所有客户的虚拟客户C′，分割C′得到满足车辆载重约束的解s″；

步骤7对s″实施VNS邻域搜索；

步骤8若s″对应总行车距离少于s，则进行替换，即s=s″，m=0，否则m=m+1；

步骤9i=i+1；

步骤10当i≤g且m≤n时，转步骤4进行后续迭代过程，否则算法结束，返回s。

步骤2的初始化解生成过程参照SAHiD，初始解的路径实际由单个客户构成。因此，步骤6中，当i=0时，层次分解策略HD的最底层聚类对象是单个客户，而当i＞0时，HD的最底层聚类对象是由RCO分割的前一迭代过程得到的路径集合。

2.2 分解策略

上述算法步骤5和6分别为对现有解的路径进行RCO切割，继而对所得路径采用HD策略聚类与分解。这里可以将RCO和HD合并，从而形成更完整的分解方法，大致步骤如下。

步骤1确定客户连接优劣的参照值L；

步骤2针对当前解sol′的每条路径，将客户连接按照L划分，分别为差连接集合P和好连接集合G；

步骤3分别从P和G各随机地选取一条连接，按照一定概率进行截断，P连接以高概率截断，而G以低概率截断，以保留好的路径结构；

步骤4步骤3截断后的路径构成集合R，R的每条路径可视为一个虚拟任务；

步骤5随机地在[1,β·|R|]产生一整数K，并以K为聚类数，对R的路径使用K方法进行聚类；

步骤6对步骤5所得每个类别的路径采用BIH方法进行排列；

步骤7将步骤6每个类别排列后的路径视作一个虚拟客户，将所有虚拟客户汇集，重新构成虚拟任务集R；

步骤8若|R|＞1，则转步骤5继续分解，否则结束。

上述步骤中，|R|为R的虚拟客户数，β为压缩系数，设置为0.1。HD的具体过程参见文献[13]，而RCO参见文献[14]。

2.3 变邻域搜索

变邻域搜索（VNS）是一种非常有效的局部搜索，在VRP的各种扩展问题中广泛应用。VNS基本思想是首先构造局部搜索算子集合，然后按照一定顺序选取集合中的算子对现有解进行邻域搜索。当搜索陷入局部最优时，采用扰动策略，以跳出局部最优陷阱。鉴于文献[15-16]中邻域搜索的良好特性，本文参照其进行VNS设计，主要包括如下部分。

（1）局部搜索算子集合。路径内的局部搜索：单点插入（SI）、交换算子（Swap）以及2-OPT；路径间的局部搜索SI、2-OPT以及两条路径的交叉算子。

（2）扰动算子集合。扰动算子实际为局部搜索算子，包括算子SI、双点插入（DI）以及Swap，每个算子分单条路径和两条路径，可认为有6种扰动算子。每次随机地选取其一进行解结构的重组，以在更大范围内搜索更优解。

（3）信息存储结构。对当前解的相关信息以及搜索记录进行存储，可以显著提高后续搜索速度。本文的VNS中亦对搜索信息进行存储，如每条路径中客户的最小需求量、最大需求量以及两个连续客户的最小和最大需求量，如此可以对SI、DI以及Swap等不满足容量约束的操作进行过滤。如有两条路径r1和r2，其中r1上客户最小需求量为6，r2上所有客户的总需求量为122，车容量Q为125，则路径r1的客户对于r2而言，所有的SI、DI都无法进行，故而可以直接将SI、DI过滤。

3 实验及分析

本文利用两个标准测试集Golden[17]与Li[1]对HD-VNS进行实验测试，以检测其问题求解能力，尤其是在大规模问题上的表现，并将实验结果与代表性的优秀算法结果进行了对比。

3.1 实验参数

测试集Golden与Li共包含32个测试样例，其中Golden的20个测试样例客户数由240升至483，属于中等规模测试集；Li的12个测试样例客户数由560升至1 200，为大规模测试集。目前，作为大规模CVRP测试集，Li已成为算法性能验证的标准数据。

本文的算法HD-VNS采用C++编程，运行环境为Intel（R）Xeon（R）E5-2650 v2，主频为2.6 GHz，RAM大小为64 GB，最大迭代次数g设置为3 000，最大无进展迭代数m设置为120。每个测试算例独立运行10次。为更好地说明算法HD-VNS的有效性，本文引用较近的工作进行比较，包括算法VNSA[7]、AVNS[3]及FJ-QACVRP[9]。

3.2 实验结果与分析

HD-VNS与比较算法VNSA、AVNS在测试集Golden与Li上的最优结果如表1和2所示。对于表1中Golden测试集，算例G9～G20的L为无穷大，即此12个算例没有最大行程距离约束，只有容量Q限制。4个比较算法的某结果若最小，则以“*”标识，表中NBS（Number of the Best Solutions）统计了各算法在相应测试集上解的最优数目。

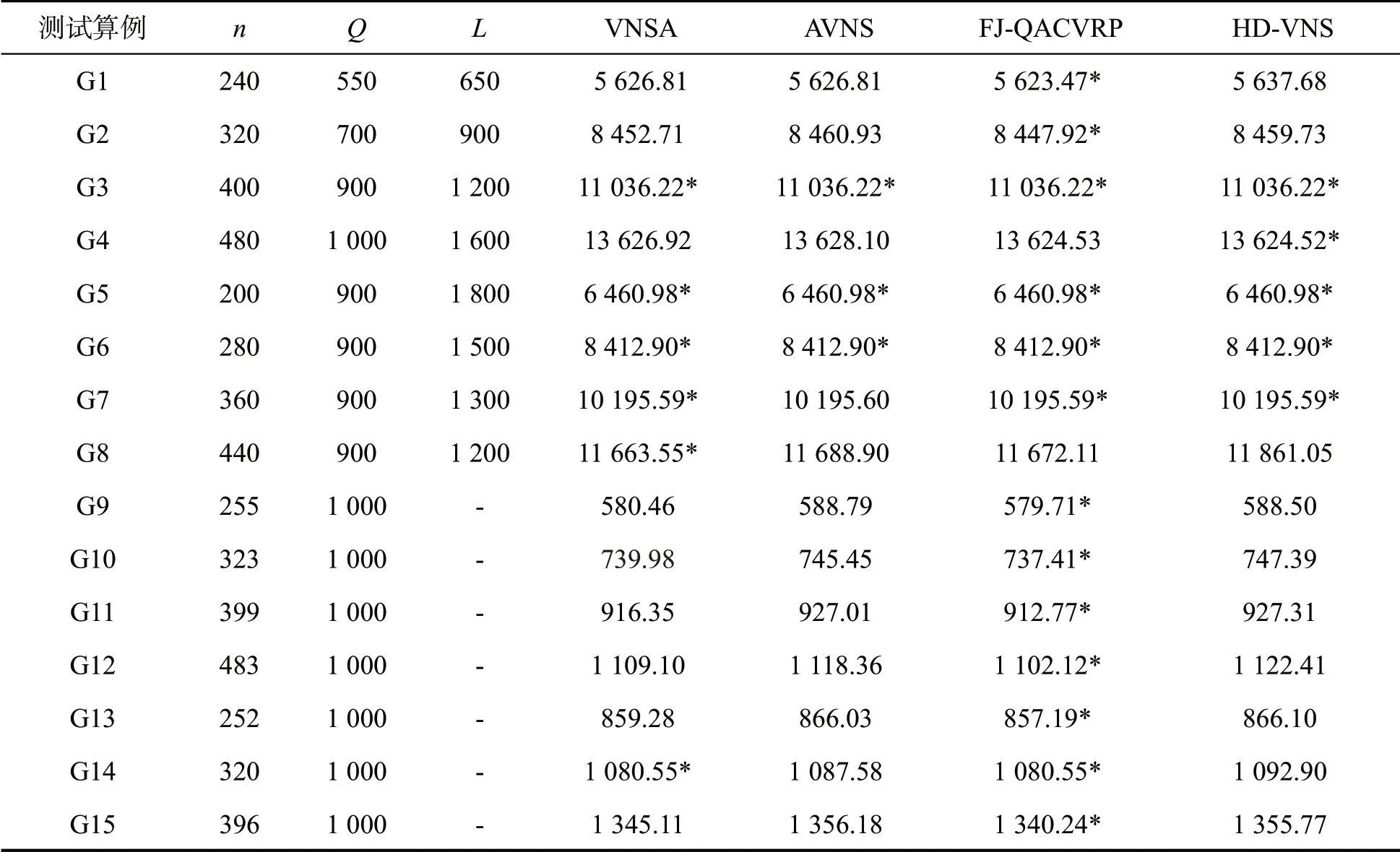
表1 测试集Golden上的实验结果

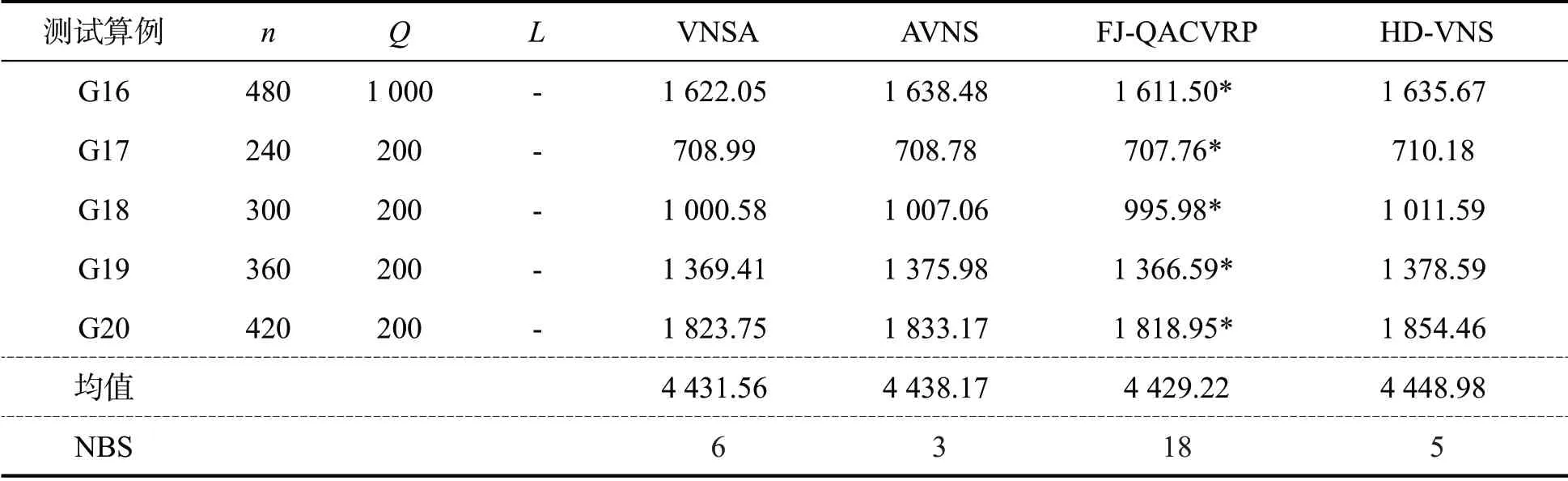
续表1

由表1可知，基于测试集Golden，FJ-QACVRP在18个算例中取得了最好值，算法HD-VNS、VNSA以及AVNS取得最好值的算例数分别为5、6和3。因此，在中等规模测试集Golden上，FJ-QACVRP具有明显优于其他算法的问题求解能力。

由表2可知，在测试集Li的12个测试算例上，算法HD-VNS总共取得了9个最好值，而FJ-QA‐CVRP、VNSA和AVNS取得最好值的算例数分别为7、2和1，少于HD-VNS，尤其是VNSA和AVNS仅在极少数算例上获得最好值。对于12个算例的平均值而言，HD-VNS的最小，为24 027.03，而FJ-QA‐CVRP、VNSA和AVNS的平均值分别为24 037.72、24 037.98和24 055.30。因此，HD-VNS在大规模CVRP上显示了良好的性能。由上述实验结果及分析可知，随着问题规模增大，算法HD-VNS求解能力趋于明显。

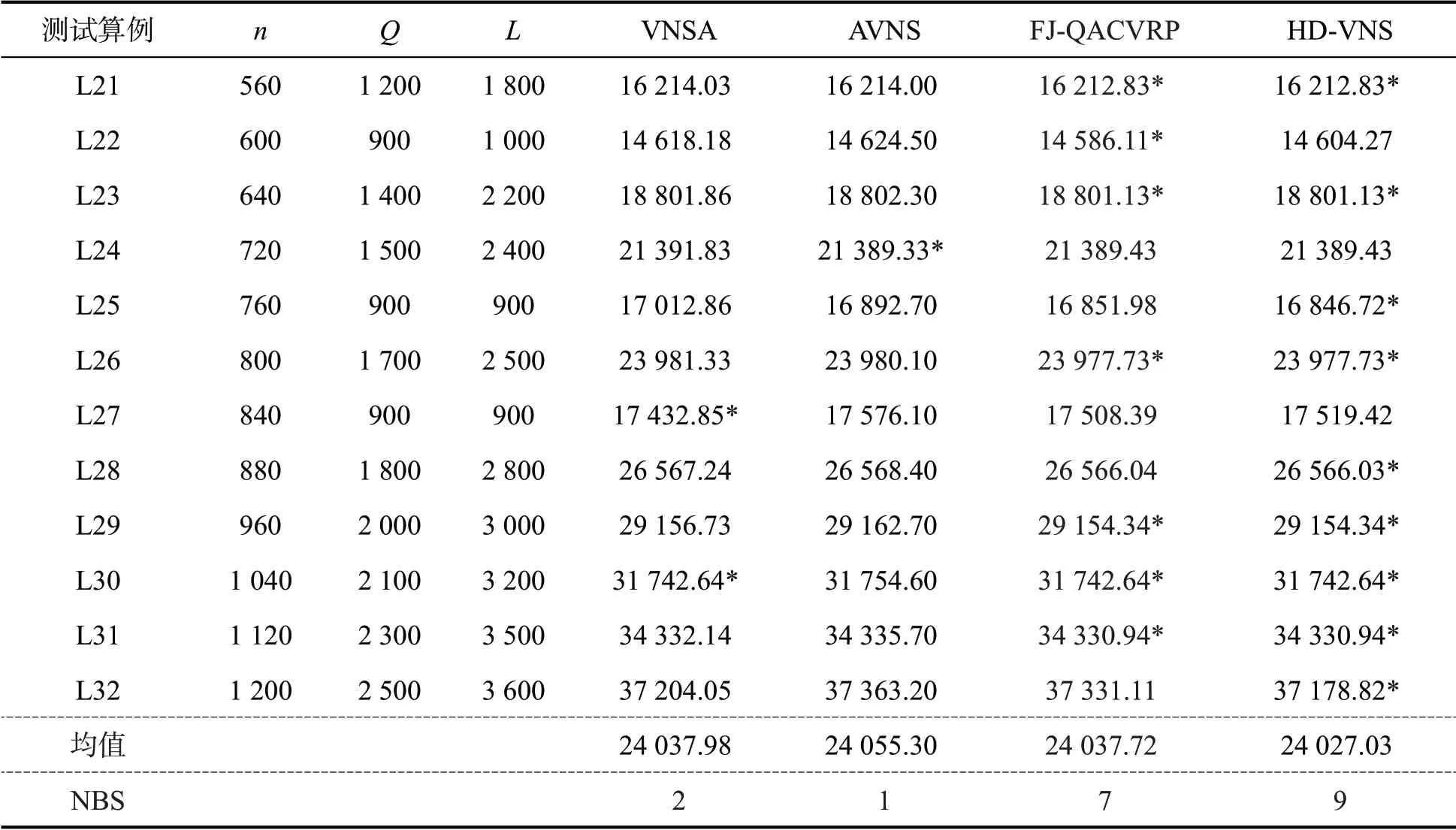
表2 测试集Li上的实验结果

4 结论

CVRP是容量受约束的一种车辆路由问题，在实际生活中，具有众多应用背景。本文针对热点问题——大规模场景下的CVRP分析，回顾了该问题的相关求解算法。将Tang提出的用于解决大规模CARP的层次分解策略引入本文，从而设计了基于分治策略的LSCVRP求解算法HD-VNS。通过对标准测试集的计算可知，HD-VNS在大规模测试集上具有良好的问题求解性能。