分数阶无线电能传输机理的提出及研究进展

张 波，荣 超，江彦伟，疏许健

（1. 华南理工大学电力学院，广东省广州市 510641；2. 福州大学电气工程与自动化学院，福建省福州市 350108）

0 引言

无线电能传输（wireless power transfer，WPT）技术自19 世纪90 年代被提出以来，一直受到国内外的密切关注。近10 年来，WPT 技术从机理研究到产业化都取得了长足的发展。特别是2007 年，美国麻省理工学院的Soljacic 教授受光学传播原理的启发，提出了基于磁耦合谐振的WPT 技术，使发射侧与接收侧产生能量交换和振荡，形成一个能量最大传输通道，实现了2 m 距离下60 W 的功率传输，效率达到40%［1］。该技术突破了感应WPT 技术的理念，具有传输距离较远、灵活性较高、传输功率等级较宽、能量只在同谐振频率的物体间高效传输、不同谐振频率之间基本无能量交换、对传输介质依赖小以及对电磁环境影响小等优点［2］，可以说是WPT 技术的一个里程碑式进展，极大激发了全球WPT 技术研究的热潮。

美国斯坦福大学的范汕洄教授于2017 年在Nature 杂志上发表了基于量子宇称-时间（paritytime，PT）对称原理的WPT 技术，实现了0.7 m 范围内约19 mW 恒定功率和90%以上恒定传输效率的稳定电能传输［3］。PT 对称原理也称为镜像对称原理，它通过控制使发射侧与接收侧互为镜像，构建了一个具有PT 对称结构的非厄米传输系统。在强耦合区域内，该系统具有纯实数特征根，可实现增益和损耗之间的平衡。因此，系统的传输功率和效率在强耦合区域内对传输距离变化不敏感，即传输功率和效率在强耦合区内保持恒定不变［2］。该技术虽然传输功率极小，但在WPT 领域引入了一个新的理念，为WPT 的机理研究打开了一扇新的大门，也是量子理论在WPT 技术中的首次应用，可以说是继2007 年磁耦合谐振WPT 技术后，又一个里程碑式的进展。

虽然磁耦合谐振和PT 对称理论促进了WPT技术的进步和发展，但仍存在不少固有瓶颈问题。例如，磁耦合谐振WPT 技术对谐振频率十分敏感，但谐振电感和电容的阻抗随材料、频率、工作环境、工作寿命而发生变化，会导致失谐，无法实现电能高效的无线传输。因此，谐振频率的稳定控制是谐振WPT 的关键。此外，近距离传输会出现功率分裂现象，导致传输特性对负载和距离的变化十分敏感，无法稳定传输功率。PT 对称WPT 技术要求发射侧与接收侧固有频率一致，同样面临接收侧失谐或负载的变化影响系统性能的难题。在大功率应用中还要解决PT 对称WPT 系统的电源问题，这些均导致其难以进一步的产业化。为此，探索和发现WPT的新机理任重道远，也是实现更远距离、更大功率、更高效率的WPT 技术的必由之路。

目前，关于WPT 机理的研究均集中在基于整数阶的数学模型上，然而越来越多的研究发现实际生活中的电感和电容均是分数阶的。此时，基于分数阶微积分的建模方法才可以更加准确地分析出分数阶电路系统所具备的特性。特别是，当分数阶阶数偏离整数阶阶数较大时，如果继续使用传统整数阶模型来分析，不仅会使结果失准，而且难以挖掘出分数阶电路系统所独有的特性。分数阶微积分理论已经在建模和控制等方面体现出了整数阶系统无法比拟的优势，但在WPT 领域还未被深入研究。本课题组受实际电感和电容的分数阶本质和分数阶微积分理论的启发，提出了一种新型的基于分数阶电路原理的WPT 技术，在国家自然科学基金重点项目支持下开展了系统研究。目前的研究成果表明，基于分数阶微积分理论的分数阶WPT 不仅涵盖了感应和谐振WPT，且在特定条件下具有PT 对称WPT 的特性，能够在中距离范围内实现恒功率、恒效率的WPT，并具备抗接收侧频率失谐或负载变化、360°方位变化的独特优点。

为便于理解分数阶WPT 机理，本文首先简要介绍了分数阶微积分理论的基本定义和发展历程。然后，介绍了分数阶元件的基本特性，并分析了2 类基本分数阶电路。接着，基于耦合模理论，分别介绍了分数阶非自治、自治WPT 机理，并从原理、结构和特性等方面与现有整数阶WPT 系统比较，从而直观地了解分数阶WPT 技术的特点。最后，对分数阶WPT 技术尚需攻克的问题、可能的研究方向和发展前景进行了展望。

1 分数阶微积分理论

分数阶微积分是相对于传统的整数阶微积分提出的，将传统的整数阶微积分运算阶次推广为分数［4］。长久以来，分数阶微积分一直停留在纯数学的理论推导上。因缺乏物理等背景学科的推动，分数阶微积分的发展也较为缓慢。随着人类对自然科学的深入认识，许多物理过程及现象无法用经典的整数阶微积分来表征，分数阶微积分开始展现出其独有的价值，被广泛用来描述具有分数阶特性的对象，更准确地揭示众多物理系统及过程的本质特征和物理机理。

1.1 发展历程

分数阶微积分的诞生可以追溯到Leibniz 和Newton 创 造 微 分 学 的 时 代［5］。 在Leibniz 与L′Hospital 来往的信件中，2 人讨论了如果微分阶次为1/2 会发生什么，而Leibniz 回信道:这将导出一个自相矛盾的论点，总有一天人们可以由它导出有用的结论。这一天正是1695 年9 月30 日，也就是分数阶微积分的诞生之日。最早对分数阶微积分作出理论贡献的是Euler 和Lagrange，Euler 在1730 年对微分阶次为分数的情形给出了自己的解释［6］，而Lagrange 则是在1772 年给出了整数阶微分运算阶次的可叠加性，但未给出该性质是否适用于分数阶微分运算的明确结论［7］。

1822 年，Fourier 给出了分数阶微分的傅里叶定义［8］。一直到1823 年，Abel 首次应用分数阶微积分求解等时曲线的积分方程。1847 年，Riemann 在Liouville 的工作基础上，进一步研究分数阶微积分的定义，提出将泰勒级数展开推广函数融入分数阶微积分定义中，并于1853 年提出了定积分形式的分数阶微积分定义［9］。随着分数阶微积分理论的进一步发展，Grünwald 在1867 年消除了Liouville 方法的限制，采用差商的极限，给出了q阶导数的定积分解析式。而Letnikov 在不知道Grünwald 分数阶微积分定义式的情况下，于1868 年用同样的方法得到了另一种表达式，即被广泛应用的Grünwald-Letnikov（GL）定义。1890 年，Krug 在将柯西积分公式推广到任意阶时，发现Riemann 和Liouville 的定积分下限不同，并形成了第1 个较为完整的Riemann-Liouville（RL）分数阶微积分定义。1967 年，Caputo给出了更便于应用的分数阶微积分的定义。

1.2 基本定义

在300 多年的发展历史中，分数阶微积分被众多研究者从不同角度给出了不同的定义，但无论是哪一种定义都有其局限性，故至今还没有一个统一的定义。较为常用且广泛被认可的定义有GL 定义、RL 定义和Caputo 定义。

分数阶GL 定义通过对整数阶微分的差分近似递推公式求极限得到［8］，其微分定义表达式为:

分数阶Caputo 定义解决了RL 分数阶微积分定义中的分数阶初值问题［10］，具有较为明确的物理意义，被广泛应用在工程领域。分数阶Caputo 微分定义表达式为:

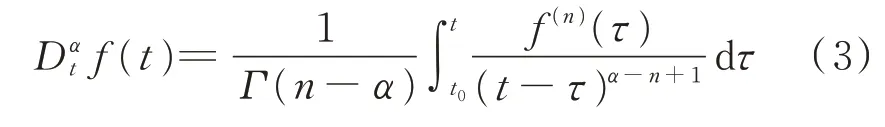
式中:0≤n-1＜α＜n。

由上述分数阶微分的定义表达式可知，分数阶微分与整数阶微分存在明显的差异，函数f（t）的整数阶导数只取决于函数f（t）在自变量t的极小邻域内的状态，而其分数阶导数不仅与t时刻的状态有关，还依赖于初始时刻t0到t时刻这个过程的状态，即分数阶的记忆特性。

值得注意的是，3 种定义并不是在任何情况下都完全等价。适用于工程领域的Caputo 微分定义在分析Buck 变换器时，其结果与实验结果是不相符的，而由RL 微分定义推导出的模型则更准确且符合实际情况［11］。此外，文献［12］通过研究分数阶RLCα串联电路阶跃响应，证明了RL 微分定义对分数阶电路的动态描述更准确且更加适用于分数阶电路的时域分析。

1.3 应用

21 世纪是分数阶微积分理论被广泛应用的元年，分数阶微积分系统又被称为“21 世纪系统”，其在各个工程领域都取得了成功的应用，包括电化学、生物医学、控制理论、电气工程等。

在电化学领域，分数阶微积分理论的首次应用源于1971 年Ichise 等人利用分数阶微积分研究电化学中扩散过程的传递函数［13］。随后，Isabel 等人利用电解过程模拟分数阶电容，研究影响容抗的因素［14］，Krishna 等人通过在电极上覆盖聚甲基丙烯酸甲酯薄膜的方法构造了一种恒相位元件，其阻抗特性在特定频段内近似等于0.1 阶分抗元件［15］。在生物医学领域，早在1933 年，Cole 就给出了生物体细胞膜电导的分数阶表征形式［4］。在控制领域，分数阶微积分因其特有的“记忆特性”，相对于整数阶具有更加精确的控制效果，被大量应用于反馈控制、信号及图像处理、系统观测等方面。1960 年，Manabe首次提出了分数阶控制的理念。随后，Oustaloup 创立了非整数阶鲁棒（CRONE）控制［16］，这种CRONE控制器比传统比例-积分-微分（PID）控制器更具优势，且物理含义更明确，是目前工业控制领域应用最广泛的分数阶控制方法之一。1999 年，Podlubny 提出了分数阶PIλDμ控制器［8］，在传统PID 控制器的基础上增加了能够影响系统性能的微分和积分阶次，具有更好的响应效果和稳定性，为分数阶控制理论的发展奠定了基础。

在电气工程领域，1961 年，Carlson 和Halijak 首次提出了分数阶电容模型［17］。1994 年，Westerlund发现整数阶微分不能精确描述电容特性，利用分数阶模型可以更好地描述电容［18］。此后，大量研究将整数阶电路模型推广到分数阶电路领域，Radwan 等人研究了基于分数阶元件的阻抗匹配网络和分数阶RCα、RLβ、LβCα、RLβCα电路的基本特性［19］，提出了分数阶滤波器的实现方法，并讨论了分数阶滤波器的基本性质。此外，分数阶混沌电路［20］、分数阶DCDC 变换器［21-22］、分数阶振荡电路等新型电路也受到了广泛的研究。

2 分数阶元件及电路

在经典电路理论中，理想的电感和电容的伏安特性都是满足整数阶微积分的，这一简单的数学关系也广泛地应用在电气工程领域。但在现实世界中，整数阶元件是不存在的，只是用整数阶来近似，采用整数阶微积分来分析电路存在固有的不精确性。因此，应用分数阶微积分能够更准确地描述自然界中各种复杂的物理特性和过程，还可以利用分数阶元件的特性提高电路的性能，发现新的电路特性。因此，分数阶微积分拓宽了电路研究、分析和应用的思路。

2.1 分数阶元件特性分析

不同于整数阶元件，分数阶电容和电感的电气符号如图1 所示。

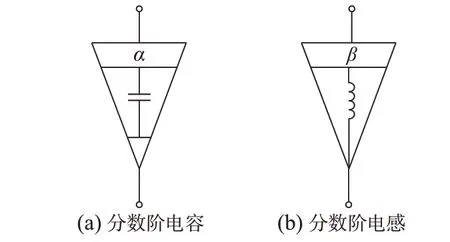
图1 分数阶电容和电感的电气符号Fig.1 Electrical symbols for fractional-order capacitance and inductance

由分数阶电路理论可知，分数阶电容和电感的伏安特性可被描述为:

式中:α和β分别为分数阶电容和电感的阶数，且满足0＜α，β＜2；vC和iC分别为分数阶电容两端电压和流过的电流；vL和iL分别为分数阶电感两端电压和流 过 的 电 流；Cα和Lβ分 别 为 分 数 阶 电 容 和 电 感 的值，其单位分别为F/s1-α和H/s1-β。

式（4）经过拉氏变换，且令s=jω可得分数阶电容阻抗ZC(jω)和电感的阻抗ZL(jω)表达式为:

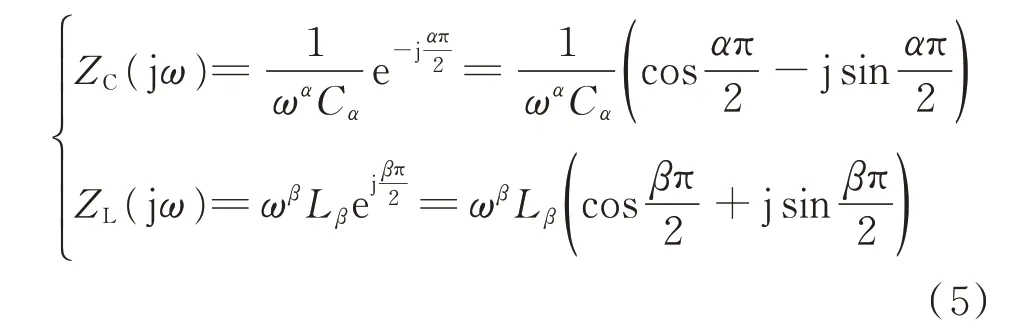
可见，分数阶元件的阻抗参数不只有电抗分量，还有电阻分量。在频域内，分数阶电容可以等效为整 数 阶 电 阻Re，Cα=cos(απ/2)/(ωαCα)和 整 数 阶 电容Ce，Cα=ωα-1Cα/sin(απ/2)的串联组合。同理，分数阶电感可以等效为整数阶电阻Re，Lβ=ωβLβcos(βπ/2) 和 整 数 阶 电 感Le，Lβ=ωβ-1Lβ/sin(βπ/2)的串联组合。这暗示了分数阶元件在阶数不为1 时，能够发出或吸收能量。

式中:T=2π/ω。

结合上述分析，当阶数α＜1 时，分数阶元件含有正电阻分量，故平均功率P＞0，消耗能量；当阶数α＞1 时，则发出能量；当阶数α=1 时，其平均功率P=0，为纯容性无源元件，即整数阶电容。根据电容 储 能 公 式W=0.5Ce，CαU2，其 中U为 等 效 电 容 上的电压幅值，结合式（5）可知分数阶电容中的电场能量为W=ωα-1CαU2Csin(πα/2)。同理，参照以上分析，分数阶电感也具有类似的性质。

2.2 分数阶元件的构造方法

现有的电感和电容元件本质上具有分数阶特性，Carlson 和Halijak 早在1961 年就提出了分数阶电容模型，随后，Westerlund 发现整数阶微分无法精确描述电容的特性，并通过实验测出了不同电介质下分数阶电容的阶数，还指出电感实际上也是分数阶的。如今，已有大量文献证明电感和电容具有分数阶特性，并通过不同方式构造出了不同阶数的电感和电容元件。

目前，分数阶元件的主要构造方法有5 种:1）基于阻抗函数的连分式分解法［23］，利用现有无源器件（如电感、电容）的串并联来近似构造阶数固定且小于1 的分数阶元件，一旦分数阶元件的阶数、容值（感值）以及工作频率改变时，则需要重新设计各电感和电容的参数，甚至整体电路结构；2）基于电化学方法［24］，即选择不同分形结构的电极表面面积、不同电介质材料等，构造阶数小于1 的分数阶电容，一旦封装完成，很难调节分数阶电容的阶数和容值；3）基于硅工艺技术，如利用场效应晶体管构造阶数固定的分数阶电容，现有文献均只涉及阶数小于1 的分数阶电容的构造［25］；4）基于运算放大器电路，可构造阶数大于1 的分数阶元件，但仅限于小功率场合的应用［26］；5）基于电力电子功率变换器［27-28］，如半桥逆变器等，构造任意阶数的大功率分数阶元件，阶数和容值（感值）可根据需要通过控制任意调节，适用于多种功率等级。

分数阶元件的构造为分数阶元件、电路及系统的特性分析和实际应用提供了技术支撑和基础。

2.3 分数阶电路

分数阶电路可以按非自治与自治电路进行分类。在自治电路中，系统的激励源不显含时间t，而不具备这种条件的电路被称作非自治电路。基本的分数阶电路一般是由分数阶电感Lβ、分数阶电容Cα和电阻R串并联组合而成的。分数阶非自治RLβCα串联电路如图2 所示。

图2 分数阶非自治RLβCα串联电路Fig.2 Fractional-order non-autonomousRLβCαseries circuit

图2 中，us为外加激励电源，u为分数阶电容两端的电压，i为流过回路的电流。该分数阶RLβCα非自治串联电路的电压方程可表示为:

电路输入阻抗Z可表示为:

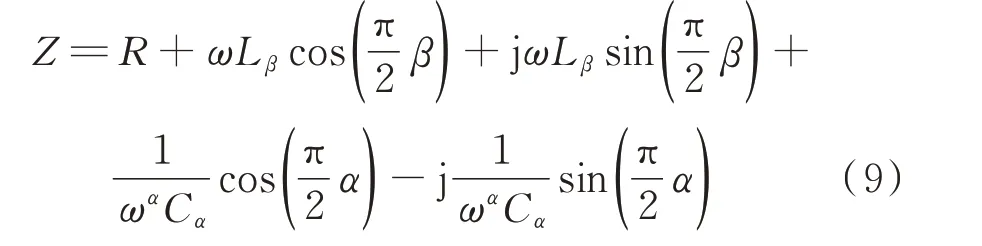
当图2 所示分数阶非自治RLβCα串联电路发生谐振时，即输入阻抗虚部为0，可得该电路的谐振角频率为:

由式（10）可知，分数阶RLβCα非自治串联电路的谐振频率不仅取决于感值Lβ和容值Cα，还可以通过控制分数阶电容的阶数α和分数阶电感的阶数β来调节。

当电路的谐振频率固定时，根据式（10）可得到不同阶数下分数阶电容值为:

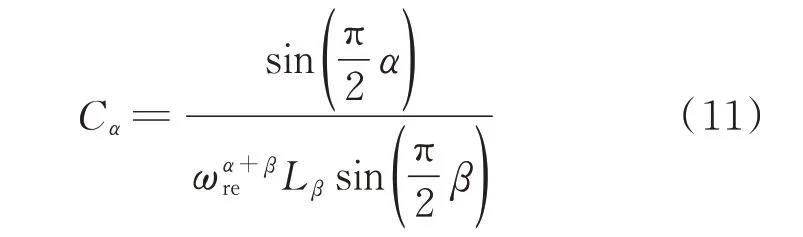
谐振状态下，电路的输入阻抗可表示为:

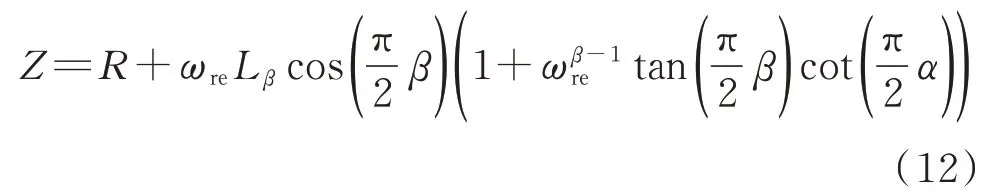
分析式（12）可知，阶数α、β的取值不同，输入阻抗表现的电阻特性也不同。假设电感为整数阶，即β=1，则当阶数α大于某一值αC时，分数阶非自治RLβCα串联电路表现为负电阻，当阶数α小于αC时，该电路表现为正电阻，而当α等于αC时，输入阻抗为0，相当于电路短路。综上所述，分数阶非自治RLβCα串联电路的阶数应远离αC，根据式（12）可得这一临界阶数αC为:

不同于整数阶系统，分数阶电路在没有激励源的情况下依然可以自发达到稳态，对应的电路被称为分数阶自治电路。分数阶自治RLβCα串联电路如图3 所示［29］。

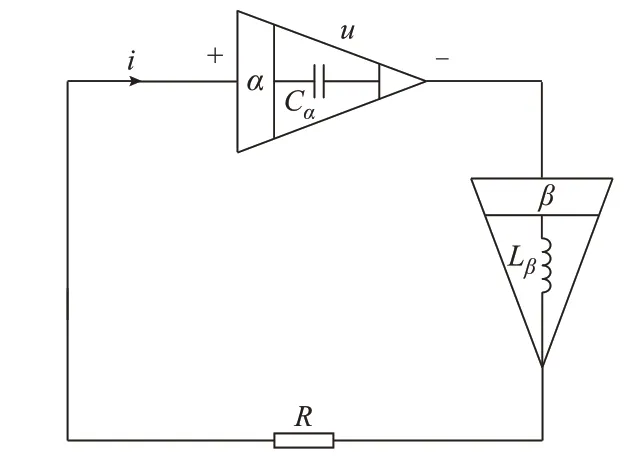
图3 分数阶自治RLβCα串联电路Fig.3 Fractional-order autonomousRLβCαseries circuit

根据基尔霍夫电压定律可得如下电压方程:

式（14）是一类典型的分数阶常微分方程，通过求解该式可以得到电路电压及电流。值得注意的是，该方程的数值解法已经得到了广泛且深入的研究，例如，基于GL 定义的离散数值解法。

为了进一步得到分数阶RLβCα串联电路的自谐振频率和电路约束条件，列出其阻抗方程为:

式中:I(jω)为回路电流i对应的相量。若式（15）中电流I（jω）有非零解，则回路阻抗须等于零，即

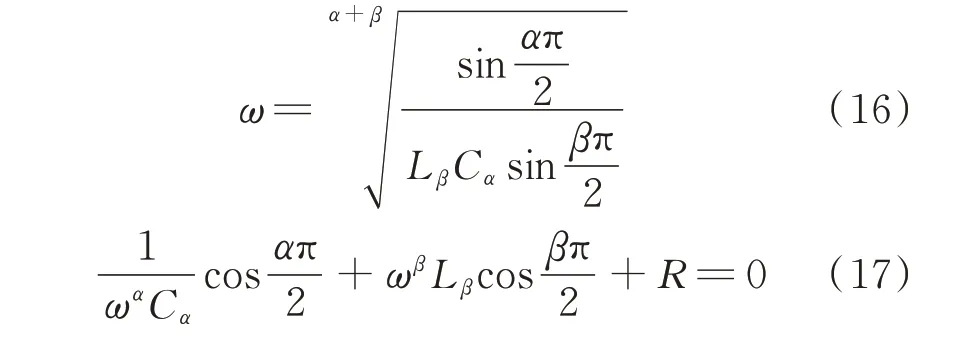
在自治的分数阶RLβCα串联电路中，谐振频率不仅取决于分数阶电容值Cα和电感值Lβ，还由分数阶电容和电感的阶数α和β所决定。在基于负电阻效应的分数阶回路中，分数阶电感值Lβ和电容值Cα须能自动调节，以满足式（17）所示的约束条件。

3 分数阶非自治WPT 机理

根据系统动力学方程是否随时间t变化，分数阶WPT 同样可以分为分数阶非自治WPT 和分数阶自治WPT。本章将对分数阶非自治WPT 的电路结构、模型和特性进行讨论和分析。

3.1 系统电路及其耦合模型

分数阶非自治WPT 系统电路的构成方式多样，包括:1）完全采用分数阶元件构成；2）采用分数阶元件与整数阶元件混合。因此，按照串联-串联型、串联-并联型、并联-串联型和并联-并联型4 种拓扑形式排列组合，有4×34=324 种基本电路结构［30］，显然比整数阶的串联-串联型、串联-并联型、并联-串联型和并联-并联型4 种基本电路结构丰富得多。

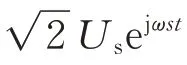
图4 串联-串联型分数阶非自治电路WPT 系统结构Fig.4 Structure of WPT system based on fractionalorder non-autonomous circuit of series-series type

根据文献［31-32］，其等效的耦合模方程可表示为:

3.2 恒流输出特性

由等效耦合模方程式（18）可知，通过调节分数阶元件的阶数，分数阶非自治WPT 系统可以灵活地实现感应式和谐振式WPT 系统的切换。值得注意的是，通过求解式（18）可得谐振状态下分数阶非自治WPT 系统的接收端模式a2为:

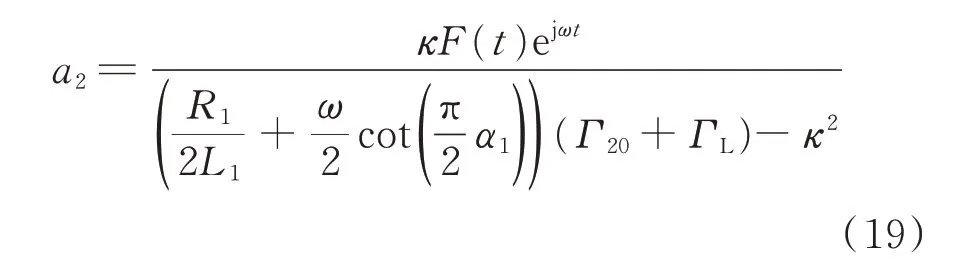
由式（19）可知，当发射端分数阶电容阶数α1被控制为式（20）所示数值α0时，接收端模式幅值|a2|=F/κ。根据耦合模理论中模式的定义可知|a2|与负载电流I2成正比，即当α1=α0时，负载电流I2仅与耦合强度有关，而不受负载因素的影响。此时，负载电阻变化时，仍然可以保持恒流输出。这一特性具有应用潜力且非常适用于需要恒流供电的负载。

根据式（18）至式（20）可进一步得到恒流输出时分数阶非自治WPT 系统的输出功率Po和效率η分别为:

在系统保持恒流输出时，分数阶非自治WPT系统的输出功率与负载电阻呈现如附录A 图A1 所示的线性关系，从而克服了整数阶谐振式WPT 的输出电流随负载电阻增大而减小的问题。此外，分数阶非自治WPT 系统传输效率随着负载电阻的增加先上升后下降，此时存在一个最优的负载电阻RL=R2(R1R2+ω2M2)/R1使得传输效率达到最大。

可见，分数阶非自治WPT 系统凭借着具有分数阶微积分特性的分数阶电容或电感，极大地增加了WPT 系统的设计自由度。在设计该系统时，可以根据WPT 系统的运行环境和要求来选择分数阶元件的阶数，从而使系统可以灵活地调节输出功率和效率或恒流输出。

4 分数阶自治WPT 原理

4.1 系统电路及其广义耦合模型

与分数阶非自治WPT 系统一样，分数阶自治WPT 系统同样有着丰富的拓扑结构。对于分数阶自治WPT 系统而言，发射电路仅有串联拓扑形式，且至少有一个有源分数阶元件；接收电路有串联和并联型2 种拓扑形式，故有2×(33+32×2)=90 种电路结构。串联-串联型分数阶WPT 系统电路结构如图5 所示［33］。

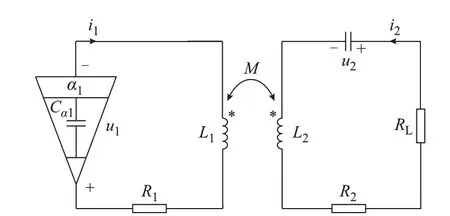
图5 串联-串联型分数阶自治电路WPT 系统结构Fig.5 Structure of WPT system based on fractionalorder autonomous circuit of series-series type

为简化分析及说明问题，图5 的分数阶系统电路仅选取发射侧电容为分数阶电容，而其他分数阶元件的阶数均取1，即整数阶数。根据文献［34］，其广义耦合模方程可以表示为:

式中:发射端总损耗率Γ2=Γ20+ΓL；Cα1的修正因子θC1=ωα1-1/sin(α1π/2)，其 他 相 关 参 数 如 表1所示。

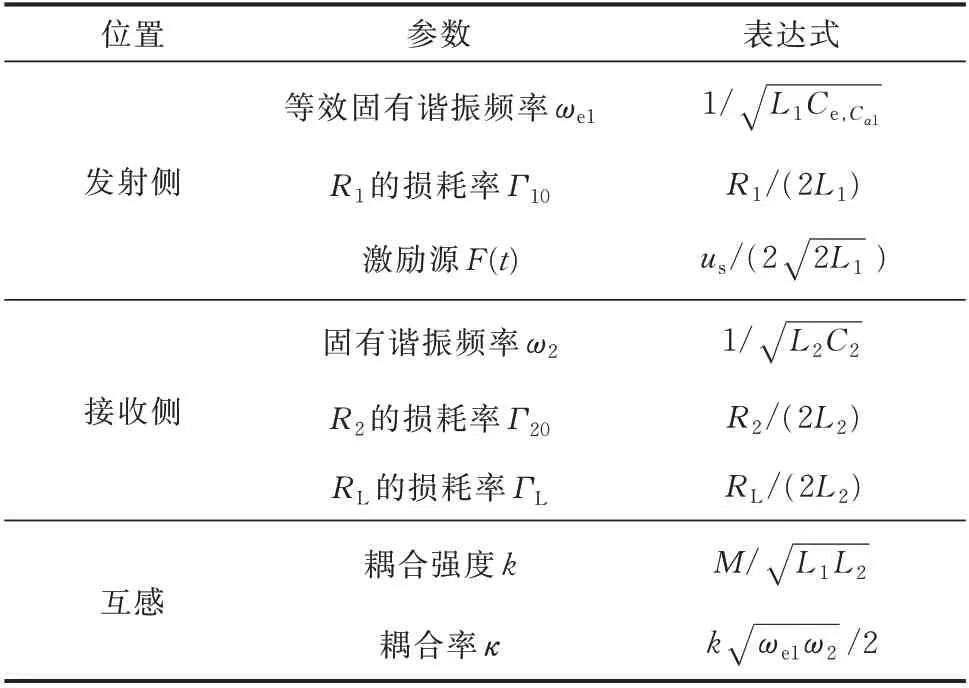
表1 耦合模方程中的主要参数Table 1 Key parameters of coupled mode equations

4.2 系统特性分析

为了进一步分析该自治系统的频率特性和性能，设a1=A1ejωt，a2=A2ejωt，其中A1和A2分别为a1和a2的幅值,将其代入式（23）中的分数阶微分项，即可得到分数阶电容所提供的等效负电阻增益系数gCα=-0.5ωe1cot(α1π/2)。因此，式（23）所示广义耦合模方程可以整理为:

得到自治系统的特征频率解后，可进一步分析系统在强耦合区域的效率和功率。根据耦合模理论能量关系，强耦合区域内系统效率表达式为:

式中:Q1为发射线圈品质因数且Q1=ω/(2Γ10)。根据耦合模理论可知，2.1 节中得到的分数阶电容电场能量即为原边模式对应的能量，即W=|a1|2。结合式（27）可得强耦合区域内系统输出功率为:

由式（27）和式（28）可知，在强耦合区（k＞kC），系统效率和输出功率与互感系数k和接收侧谐振频率均无关。

4.3 系统实现

分数阶自治WPT 系统的电路原理如图6 所示。其中，分数阶电容由受控的半桥变换器构成［27］，且其阶数大于1，可向系统提供增益。

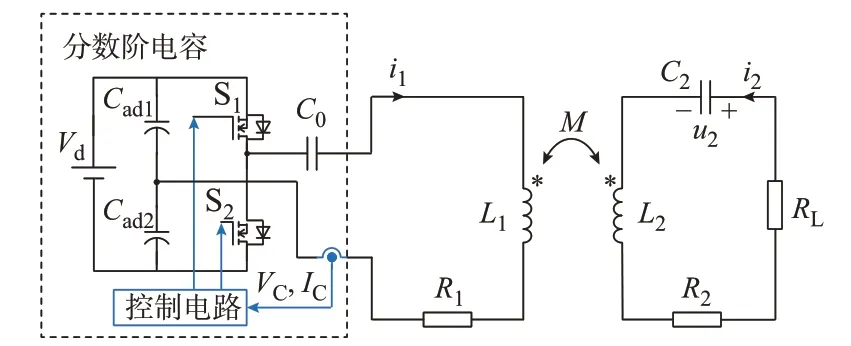
图6 分数阶自治WPT 系统的电路原理图Fig.6 Circuit principle diagram of fractional-order autonomous WPT system

电路参数的取值如表2 所示。其中，发射侧和接收侧内阻包含电容器内阻和线圈本身的内阻。电容器内阻利用阻抗分析仪测量，线圈内阻利用反射测量法获得高频下的内阻值［35］。

表2 实验电路参数Table 2 Parameters of experimental circuit

4.4 仿真与实验分析

在接收侧无失谐情况下，分数阶自治WPT 系统的系统效率和输出功率随传输距离的变化曲线如图7 所示（分数阶电容阶数α1取1.02）。

图7 系统效率和输出功率随传输距离的变化曲线Fig.7 Variation curves of system efficiency and output power with transmission distance

附录A 图A2 为不同分数阶阶数条件下分数阶系统传输效率和输出随耦合强度的变化曲线。由图A2 可知，通过调节分数阶元件的阶数就可以灵活地改变临界耦合强度以及系统效率和功率，这也是传统整数阶系统无法比拟的优势之一。值得注意的是，在期望通过增大阶数来提高系统功率和效率的同时，临界传输距离也会随之缩短。在实际应用时，应根据性能要求综合设计分数阶系统和控制电路。

可见，分数阶自治WPT 系统借助阶数大于1 的有源分数阶元件，在无需正弦激励源的情况下仍可为负载提供能量。由于分数阶元件特有的频率特性，该系统可以自适应地平衡系统损耗以及调节分数阶系统的谐振频率，从而表现出稳定的传输特性。在WPT 新机理的研究过程中，非线性系统以及自治系统还存在很多独有的特性有待挖掘。

5 与其他WPT 系统及机理比较

由前文的论述和分析可见，分数阶WPT 机理是以分数阶电路为基础的，且与整数阶WPT 机理有所不同。本章将对分数阶自治WPT、谐振式WPT 和基于PT 守恒原理的WPT 系统的结构及其特性进行比较。其中，谐振式WPT 系统是典型的非自治WPT 系统，而基于PT 守恒原理的WPT 系统是以自治电路为基础的WPT 系统。从电路拓扑结构和运行机理的角度分析，分数阶WPT 系统完全不同于谐振式WPT 和基于PT 守恒原理的WPT系统。

表3 对比了3 种WPT 系统的电路拓扑。谐振式WPT 系统由高频交流源和2 个固有谐振频率相等的回路构成。基于PT 守恒原理的WPT 系统由一个具有非线性饱和增益的负电阻为系统提供能量，以保证能量在增益和损耗之间平衡流动。分数阶自治WPT 系统采用分数阶元件，由阶数大于1 的有源分数阶元件作为系统的增益为负载供能。

表3 3 种WPT 系统的结构对比Table 3 Comparison of structures of three kinds of WPT systems

为了便于从理论上比较3 种系统的特性差异，本章仿真参数设定为:R1=R2=0.4 Ω，RL=9 Ω，L1=L2=100 μH。根据耦合模理论，表4 列出了3 种系统在强耦合区域中系统效率和输出功率的表达式，并给出了分数阶自治WPT 和基于PT 守恒原理的WPT 自治系统的强耦合区域。附录A 图A3 为3 种WPT 系统的效率和输出功率随耦合强度的变化曲线对比图。可见，在强耦合区域，分数阶WPT 系统与基于PT 守恒原理的WPT 系统均表现出强鲁棒性，即通过系统本身的能量平衡机制使得效率和输出功率保持恒定；在弱耦合区域，基于PT 守恒原理的WPT 系统只有谐振频率一个稳定解，从而与谐振式WPT 系统具有相同的运行特性。

表4 强耦合区域中系统效率和输出功率的比较Table 4 Comparison of system efficiency and output power in strongly coupled regions

在实际WPT 系统中，由于互感系数和负载等因素的变化，传统整数阶系统的实际参数将偏离设计值，从而不可避免地引起失谐。因而，接收侧失谐是WPT 系统设计需要考虑的情况之一。在强耦合区域，当接收侧的固有频率偏离谐振频率时，3 种系统的系统效率和输出功率同样表现出如附录A图A4 所示完全不同的特性。谐振式WPT 系统通过2 个谐振器共振使得能量可以在其之间高效传递，因此，当接收侧固有频率偏移谐振点时，效率和输出功率将急剧下降。同样，为了保证PT 反转不变性，基于PT 守恒原理的WPT 系统也必须保证接收侧和发射侧的固有频率相等。由表4 所示的强耦合区域中系统效率和输出功率的表达式可以看出，在谐振式WPT 系统和基于PT 守恒原理的WPT 系统中，它们均与接收侧固有谐振频率ω2有关，而在分数阶自治WPT 系统中则与ω2和耦合强度均无关，表明分数阶自治WPT 系统具有抗接收侧失谐的特性。实际上，这得益于第2 章提到的分数阶元件所特有的频率特性。当分数阶元件的阶数被控制为恒定时，其提供给分数阶系统的有功功率和无功功率的比例将保持恒定，进而使系统具有稳定的传输特性。另一方面，分数阶自治WPT 系统的运行频率取决于主电路的参数，这是与采用正弦激励源的谐振式WPT 系统最显著的不同。正是分数阶特性以及自治电路的频率特性，才使得分数阶自治WPT 系统有着独特的传输特性。

6 结语

WPT 技术是国际上的热点研究方向。然而，产品化和大规模的产业化还有赖于更多基于新原理、新方法的WPT 方式，分数阶WPT 机理及技术的提出就是一个尝试。目前的理论分析和实验表明，与现有整数阶WPT 系统相比，分数阶WPT 系统具有以下优势:1）系统电路拓扑多样，比感应式WPT 系统电路拓扑更丰富，适应面更广；2）除了分数阶非自治WPT 系统形式外，还有分数阶自治WPT 系统形式，因此，可涵盖PT 对称WPT 技术的特性，且克服了接收侧频率和负载的变化导致特性劣化的瓶颈；3）分数阶谐振WPT 系统的谐振频率不仅取决于电感、电容值的大小，还取决于它们的分数阶数，且它们之间呈非线性函数关系，因此，系统具有抗失谐能力强、鲁棒性强等特点；4）由分数阶元件构成的阻抗补偿网络，不仅可以灵活调节电感、电容值，还可以控制它们的分数阶数，因此，比整数阶感应WPT 补偿网络更灵活，效果更好。可见，分数阶WPT 系统可以克服复杂的运行条件，并满足多种传输特性的要求，使其在动态无线充电、高效电动汽车无线充电和一对多WPT 系统中有着很好的应用前景。

然而，对分数阶WPT 机理及技术的研究才开始不久，还有许多特性没有认识清楚。例如，在特性研究方面，目前主要对分数阶WPT 系统的稳态特性进行了研究，对于分数阶的动态特性尤其分数阶记忆特性在WPT 过程的作用还有待进一步探索。在建模方面，分数阶耦合模型的建模方法是否可以沿用整数阶的形式，分数阶电路模型的分析方法是否存在更具一般性的理论，以及如何获得更加精确的分数阶WPT 系统的机理描述等关键性问题，都有待进一步开展深入的研究和探讨。因此，分数阶WPT 系统的研究还有一段漫长且曲折的道路要走。随着分数阶微积分原理的成熟和分数阶元件构造新方法的出现，分数阶WPT 技术的应用领域将越来越广泛。

WPT 技术能否像特斯拉预言的那样，在世界任何一个地方都能自由接收电能，还须突破一些思想、概念上的约束。特别是，目前将感应WPT 技术作为一种方式的WPT 技术分类方法，可能会制约机理研究的发展。因为电磁感应是麦克斯韦理论的通俗解释，是电磁现象的基本规律，而在此基础上发展起来的WPT 机理才是有效提高WPT 的技术。这可以类比于交流调速，调频是调速的基本原理，在此基础上发展起来的开环恒压频比（V/F）控制、矢量控制、直接转矩控制等，才是真正实用、有效的调速技术。现有感应WPT 技术实质上是阻抗匹配或无功补偿技术的应用。因此，将感应WPT 技术改为基于阻抗匹配的WPT 技术更为合理。这也避免了将谐振WPT 技术与感应WPT 技术混为一谈的误区。WPT 技术更为恰当的分类应该是阻抗匹配WPT 技术、谐振WPT 技术、PT 对称WPT 技术以及新的WPT 技术，从而鼓励人们大胆探索，发展出更多、更好的WPT 机理和技术，加快WPT 的发展进程。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。