继电保护装置带状拟合寿命模型及其弹性退役决策方法

南东亮，王维庆，张 陵，熊小伏，杨国生，何雨霏

（1. 新疆大学电气工程学院，新疆维吾尔自治区乌鲁木齐市 830047；2. 国网新疆电力有限公司电力科学研究院，新疆维吾尔自治区乌鲁木齐市 830011；3. 输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400030；4. 中国电力科学研究院有限公司，北京市 100192）

0 引言

继电保护装置的寿命评估、检修退役决策直接关系到电网运行安全［1-2］。寿命评估不准确导致的设备提前退役会造成浪费，而延迟退役则可能导致保护装置的错误动作，给电网带来极大安全风险。如何依据众多继电保护装置的失效数据，刻画出装置的失效规律并做出准确的寿命预测，一直是继电保护设备制造企业和运维部门关注的重点。

继电保护装置的寿命长短取决于其失效发生的频度，装置的失效率及其变化是用于描述继电保护装置寿命的关键参量［3］。从较长的时间尺度看，继电保护装置的失效率通常以恒定失效率表示［4］；但随着季节变换等因素，时变失效率又进一步被细分为偶然失效率与老化失效率［5］。近年来，文献［6］使用灰色线性回归组合模型，进行了保护装置的可靠性分析。为了使分析过程更加贴合设备的实际规律，部分文献还考虑了役龄回退［7-8］、恶劣天气［9］、谐波污染［10］、随机不确定因素以及数据缺失等问题［11-12］。

从变化规律上来看，装置的失效率随时间变化的趋势具有相似的特征，通常用曲线拟合失效数据表达该特征［13］，拟合曲线多形似浴盆，故常被称为“浴盆曲线”。由于继电保护装置的失效与环境、运维水平、制造质量等多种因素有关，因此，失效数据随时间变化具有较大的波动性［3］。研究人员一直在研究拟合方法，以使经过不断修正和改进的浴盆曲线能够逐渐贴合装置的实际失效特征［14-15］。拟合函数的具体形式上，Gaussian、Gamma、Weibull 常被用来进行浴盆曲线的拟合［16-17］，其中，二参数或三参数的Weibull 函数的拟合效果与装置实际失效规律的贴合程度更好［18-19］。拟合过程的误差控制多采用最小二乘法进行，但该方法容易陷入局部最优，且部分数据在处理时无法快速收敛。鉴于此，有文献提出了采用平均秩次法［18］、智能算法［20-21］、改进迭代法等来减小拟合带来的误差［22］。

在失效率变化曲线的基础上，可通过设定许用失效率来进行寿命预测与退役决策［23］。工程中还可以采用试验的方法间接实现寿命预测［24］，但由于试验环境与装置实际运行环境存在一定差距，预测结果与实际寿命通常偏离较大。此外，还有研究提出通过在线监测的方式诊断继电保护装置的状态，但目前还不能用于对装置的寿命预测及退役决策［25］。

如上所述，传统的继电保护设备寿命模型是期望用一条曲线来反映保护装置的失效规律，但由于保护装置的可靠性受多个随机因素影响，单一曲线拟合的精度显然具有较大的不确定性。以此作为运维或退役决策的依据必然偏于保守或偏于激进，付出的将是经济代价或安全风险代价。

为克服单曲线寿命模型的弊端，本文依据失效数据区间分布特征，提出一种新的带状模式的继电保护装置寿命建模方法，用以解决单条曲线拟合可能出现的拟合误差大、不能准确反映保护装置寿命变化趋势的问题。

1 继电保护装置失效分析

1.1 装置失效分析

引起继电保护装置失效的原因可以分为硬件、软件或其他原因，具体的细化分类可见附录A表A1。

针对中国西北某省级电网继电保护装置失效记录进行统计，并进行失效率计算，结果如图1 所示。

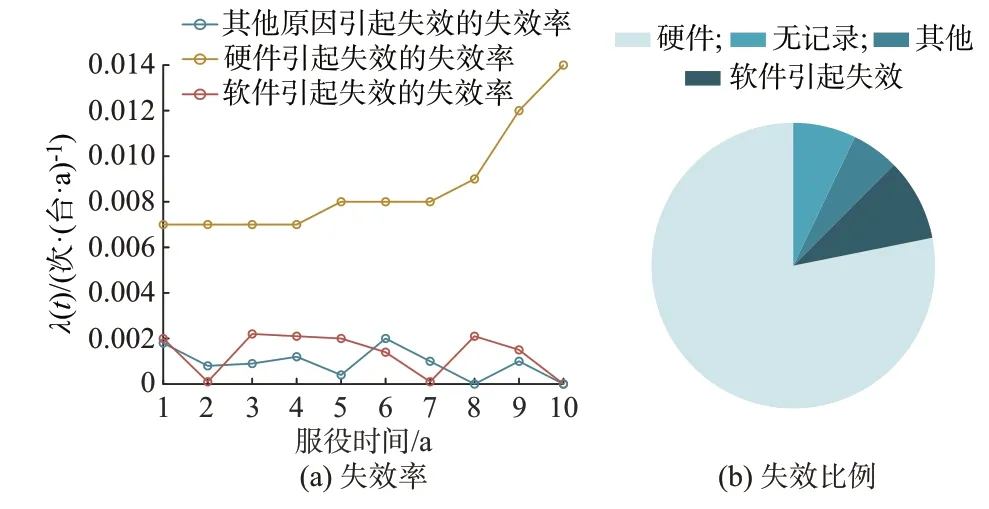
图1 各种失效原因的失效率及比例Fig.1 Failure rate and proportion of various failure causes

由图1 可知，由硬件原因引起的失效事件占比最多，且其失效率随装置服役时间的增加逐渐升高，其变化趋势具有较好的时间特征；而软件及其他原因对应的失效率相对较低，且时间特征不明显、失效的偶然性较强。需要注意的是，装置缺陷并不一定引起失效，因此在计算失效率时，需选择装置的失效记录而非缺陷记录来进行计算。

上述继电保护装置运行实际表明，由硬件引起的失效是影响保护装置寿命的主要因素。因此，本文把继电保护装置的硬件失效特征等同于保护装置的寿命变化规律。

1.2 设备寿命通用模型

由硬件原因导致的装置失效率的时间特征，通常呈现阶段性规律。从装置投入到退役的整个全寿命周期内，失效率具有以下特征:在寿命初期或“早期失效期”，失效率的初始值较高，但随着装置运行年限的增加，失效率也迅速降低，因此曲线呈快速下降趋势，这一阶段的特征主要与制造过程中工艺的波动性、材料强度的不确定性所产生的累积效应有关，但对于出厂后投入使用的设备，一般不考虑此阶段；在寿命中期或“偶然失效期”，装置的失效率降至最低水平，此期间装置失效的原因多为人为误操作或环境条件突变等；在寿命后期或“损耗失效期”，装置失效率随服役年限的增加出现上升趋势，这一特征通常是由设备使用年限较长而出现的老化、受潮、产品劣化、强度退化等造成。由于上述失效率-时间曲线整体形状形似浴盆，故称为“浴盆曲线”，如图2 所示。

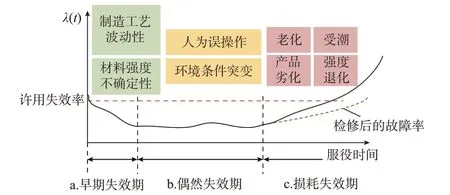
图2 浴盆型失效率曲线Fig.2 Bathtub-curve of failure rate

浴盆曲线可以由形状参数及尺度参数可调的Weibull 函数表示，且已有研究验证了Weibull 分布对装置失效数据的拟合精度要高于Rayleigh 分布、Gaussian 分 布、Gamma 分 布 等［5，17］。Weibull 分 布 函数F(t)为:

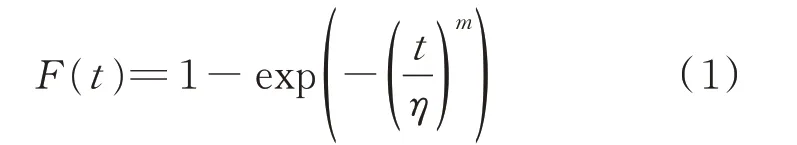
式中:t为装置投运时间；m为形状参数；η为尺度参数。

其对应的失效率λ(t)如式（2）所示:

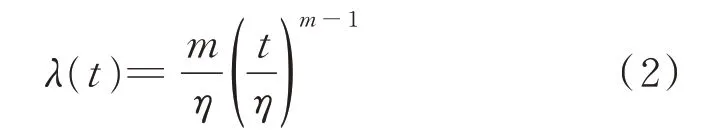
当m＜1 时，失效率函数是指数为负的幂函数，表示浴盆曲线的早期失效期；当m=1 时，失效率函数为常数，表示浴盆曲线的偶然失效期；当m＞1时，失效率函数为指数为正的幂函数，即表示浴盆曲线的损耗失效期。因此，分段的Weibull 函数能够对应浴盆曲线在不同阶段的时间特征，但拟合的精度则取决于实际装置失效数据的分散程度。显然，失效率数据的聚集度越差，拟合精度越差。

2 基于带状拟合的继电保护装置寿命模型

2.1 继电保护装置带状寿命模型思路

1）保护对象分类

通常，不同继电保护装置制造企业其产品可靠性可能存在差异。为了反映其差异，将保护装置按同源性原则进行分类研究其寿命问题。

有2 种分类方法:一是按保护设备制造厂家的型号分类，即针对不同厂家、不同型号的保护装置按类别分别进行失效率统计和寿命建模，称之为同型设备和同型设备寿命模型；二是将继电保护设备按硬件平台分类。这是因为现有继电保护设备厂家通常用统一的硬件平台作为多个型号继电保护装置的硬件，安装不同的软件实现不同的保护功能。由于采用了相同的硬件平台，其寿命分布应具有基本相同的特征。因此，可针对统一硬件平台的保护设备进行失效率统计和寿命建模，将这类保护设备称之为同平台设备和同平台设备寿命模型。

2）带状寿命模型特征

如图3（a）所示，黄色折线为某型号保护装置失效率散点连线，受运维水平、环境等多因素影响，在不同的服役期间其失效率具有波动特征。黑色虚线是按Weibull 函数拟合的变化曲线，可见其与波动数据之间的误差。

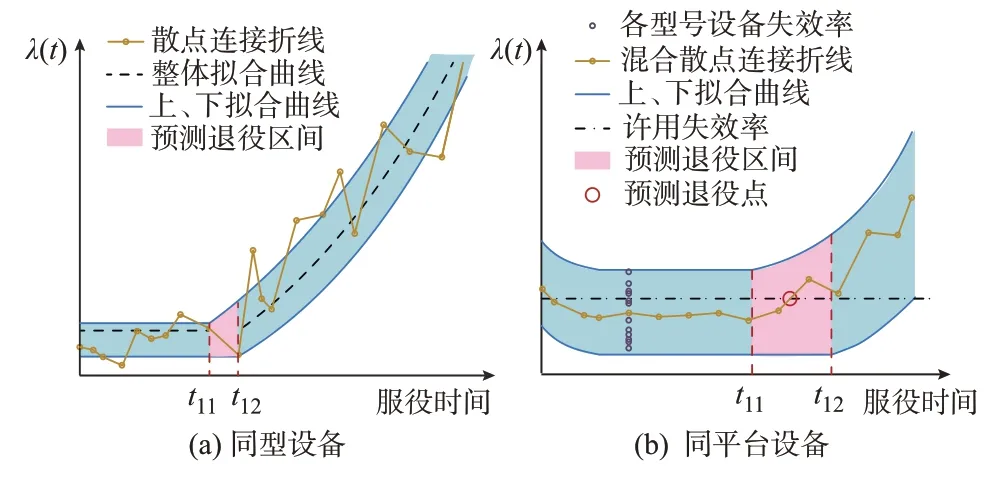
图3 同型和同平台设备失效模型示意图Fig.3 Schematic diagram of failure model for equipment of the same type and platform

因此，在建立带状模型时需寻找2 条包络线，使包络线所夹的区域为保护装置失效数据的聚集区。该区域具有带状特征，称之为继电保护装置的带状失效区间。该区间及其变化趋势反映了继电保护装置的寿命演变过程。带状模型中的包络曲线经由拟合而成，因此需要将失效率数据散点根据聚集特征划分为上包络线拟合区与下包络线拟合区。为准确表征设备整体特征与设备统计特征，使用同型设备（即指定范围内同一型号的设备）以及同平台设备（即指定范围内同一平台的设备）进行关联分析。

对于同型设备，两区域之间的分界线可采用平均值分割法或拟合曲线分割法。本文建议采用拟合曲线分割法，即先依托失效率散点用Weibull 函数拟合获得拟合曲线，以此线为界，高于界线的为上区，低于界线的为下区，然后分别对上区和下区数据进一步进行包络线拟合，如图3（a）所示。

对于同平台设备，可采用“同平台设备失效率数据累加法”将该平台相同型号不同的保护设备失效率数据进行累加后再采用前述相同方法求取上下包络线，形成带状区间，进而用图3（b）的方法建立寿命模型。

除此之外，本文还对同平台设备的寿命模型尝试用“同平台设备失效率散点带状法”进行分析。因同平台设备中的设备类型较多，但不同设备类型的数量存在较大差异，如果用所有设备类型的失效数据进行累加，则会淹没数量较少设备的运行特征。因此，在处理同平台设备失效数据时，保留每种设备的失效率数据，用所有类型的失效率数据构成散点带，由此观察全部同平台设备的失效特征，再根据这个失效率数据带来拟合其上下两条边界，即对同平台设备的失效率最大值和最小值进行拟合，以掌握这些同平台设备的失效特征。

设f1(t)为失效率数据上包络线，f2(t)为其下包络线，则带状失效率区间的宽度W(t)为:

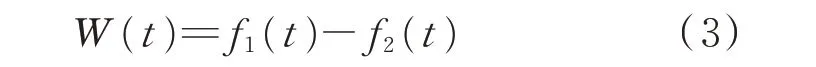
2.2 继电保护设备的失效率

设定研究对象为同型保护装置或同平台保护装置群体，建立如下动态失效率模型。

失效率的计算公式如式（4）所示:

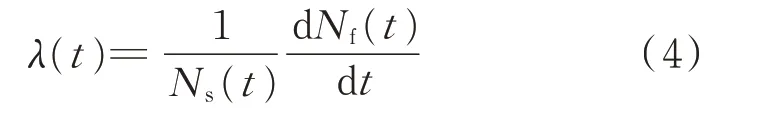
式中:Ns(t)为统计区间的保护装置总数；Nf(t)为寿命期t时刻已出现失效的保护装置总数。

2.3 带状寿命模型的建立

如前所述，带状模型需要确定区域的上下包络线，其实施步骤如下。

1）基于数据区中线拟合进行上下区域数据划分带状模型的核心是将散点分布的失效率数据分为上下2 个数据带，然后分别寻找上下数据带的拟合曲线。因此，首先需要对原始数据区进行上下区块划分，而划分的前提是先找到数据区块的中线f0(t)。

本文假设可用Weibull 函数拟合得到失效率散点的中间线f0(t)，获取f0(t)的相关参数后，可得到式（5）和式（6）。

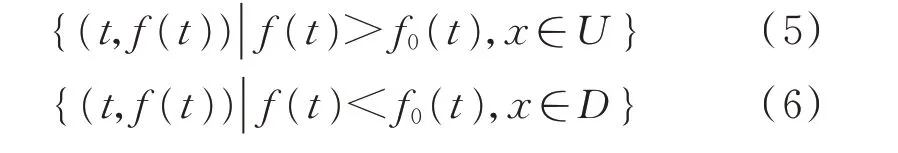
式中:f(t)为失效率散点；U为上区域散点集合；D为下区域散点集合。

在拟合中心线时，为使拟合误差更小，本文拟采用Levenberg-Marquardt（L-M）法进行拟合［22］。L-M法在迭代开始时，具有初始下降量大、迭代迅速、鲁棒性好的特点，减小了对初值的依赖性，在迭代末端，阻尼因子接近0，具有牛顿法二阶收敛性，避免最速下降法的锯齿形现象。得益于此法的强鲁棒性，拟合过程稳定且不易陷入局部最优，是目前解决已知非线性关系式参数估计的有效方法之一。

Weibull 函数即为非线性函数f0(t)，其通用表达式为:

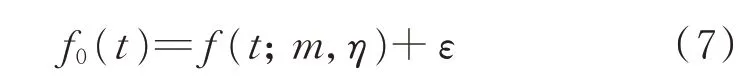
式中:ε为随机误差项。

为方便描述，用未知参量b指代未知参数m和η，初始失效率函数在经过泰勒展开（见附录A 式A1），并使一阶偏导为0（见附录A 式A2）等运算后，二参量Weibull 函数的未知参量集计算方法如式（8）所示。

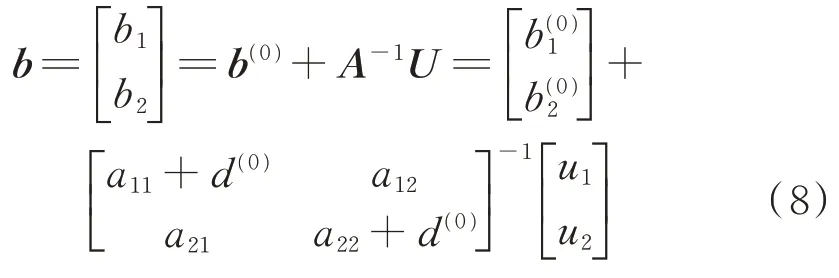
式中:a11、a12、a21、a22和u1、u2分别为由附录A 式（A3）计算所得结果；b(0)1、b(0)2分别为未知参数的初值；d为人为添加的阻尼因子，d（0）为其初始值。

如果求得的b与b（0）之差的绝对值很小，则认为拟合效果可以接受；如果较大，则把新的b作为初值代入式（8），从头计算，反复迭代，直到b与b（0）之差满足收敛条件为止。为提高效率，同时变化阻尼因子d，配合残差平方和的计算，将b用m和η回代表示，有

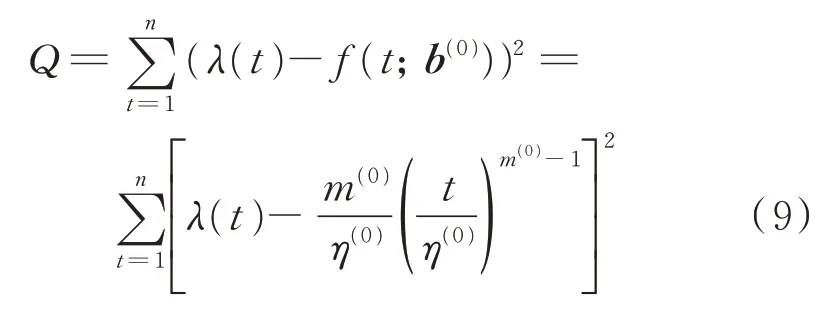
式中:Q为残差平方和。

令d（1）=10gd（0），其中g=-1，0，1，2，…，依次取值，作为环内迭代，计算出新的残差和Q′，如果Q′＜Q，则第2 次迭代结束；如果Q′≥Q，则令g=0，并逐渐增大，重新计算残差和，直到结果小于上一轮计算出的结果，则迭代结束。

2）上下包络线拟合

在利用L-M 法得到中间分界线f0（t）后，根据式（5）和式（6）确定上包络线数据集，即上包络线数据集如式（10）所示。根据Dh采用Weibull 函数和L-M 法得到对应的拟合包络线为f1（t）。

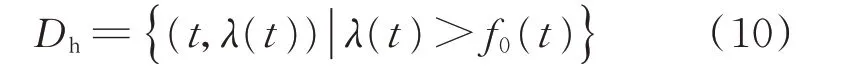
类似地，下包络线数据集为:

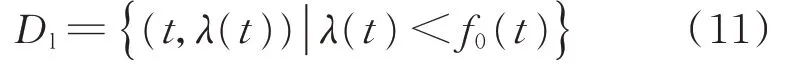
根据Dl采用Weibull 函数和L-M 法得到对应的拟合包络线为f2（t）。

3）设备失效期判断

当拟合得到上下包络线后，可分别根据上下包络线判断设备目前所处的状态，即设备是属于偶然失效期还是属于老化失效期。其中的拐点是判定这两个状态转换的关键点。

以这一曲线与实际失效率数据的总误差最小为目标，确定其中最佳的分界点。其中，第e个时间节点对应的总误差Se可由式（12）计算得到:

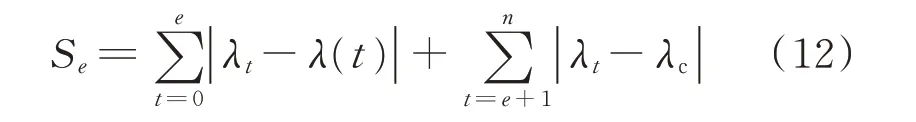
式中:λt为t时刻对应的实际失效率；λc为选定分界点处对应的失效率。

带状失效率模型中的单条曲线数学表达式如式（13）和式（14）所示。

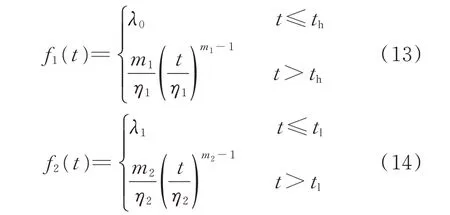
式中:m1、η1、m2、η2分别为对应f1(t)、f2(t)的未知参数；th和th之前时段的失效为偶然失效；tl和tl之后时段的失效为老化失效；λ0为th时设备所对应的失效率；λ1为tl时设备所对应的失效率。

2.4 拟合有效性检验

老化失效期的拟合效果可以通过确定系数Rsquare进行判断，Rsquare的计算方式如式（15）所示。

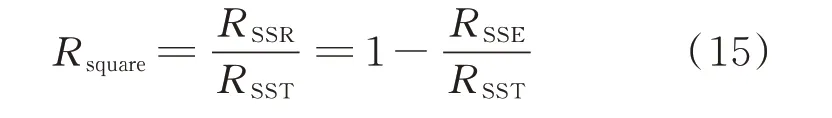
式中:以上拟合线f1（t）为例，RSSR为拟合数据与原始数据之差的平方值，如式（16）所示。

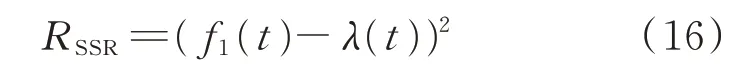
RSST为原始数据λ(t) 和均值λˉ之差的平方和，有

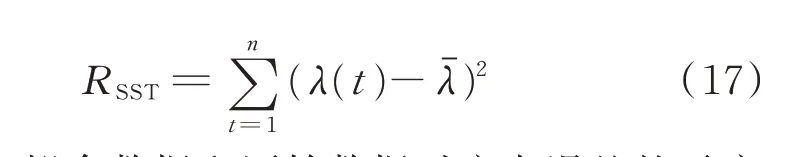
RSSE为拟合数据和原始数据对应点误差的平方和，有

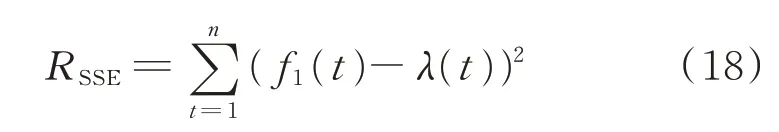
Rsquare越接近1，表示拟合效果越好。

因此，拟合有效判据为:

式（19）满足时视为拟合检验通过。通常，Rset取值为0.8～0.9。

3 设备的弹性检修退役策略制定

对于拟合得到的上、下2 条曲线，在2 个最佳分界点th、tl之间的区域，即为预测的装置推荐退役时间区间，如图4 所示。

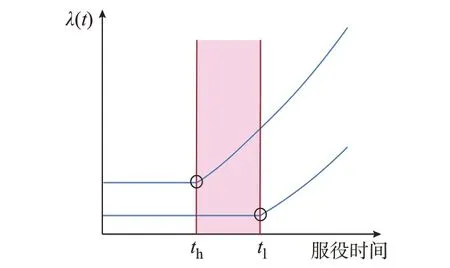
图4 退役观察区间示意图Fig.4 Schematic diagram of decommissioning observation interval

3.1 退役指标的选取

设备在进入退役时间区间的下限th后，失效率会出现逐渐增高的趋势。为保证电网的运行可靠性，应对设备相应指标严格监测，定义拟合曲线斜率作为反映设备失效率的变化情况，即:曲线斜率Kf1、Kf2分别表示曲线的切线关于坐标轴倾斜程度的量，上、下包络线的曲线斜率分别为式（20）和式（21）:

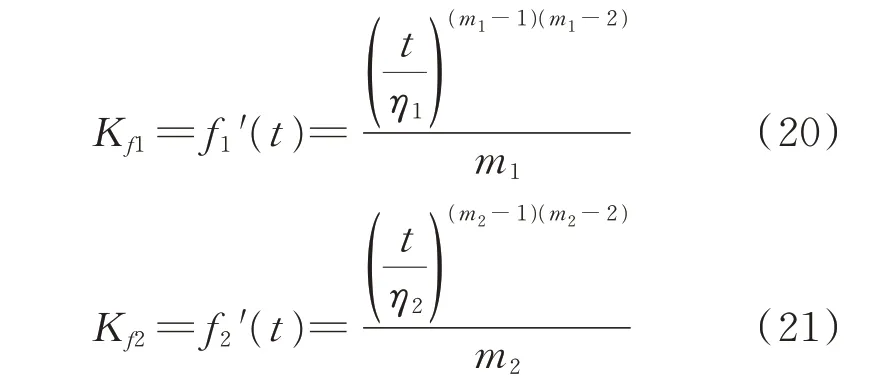
3.2 退役策略

由于设备在th之前应属于偶然失效期或者损耗失效期前期，属于运行观察期可以适当拉长检修周期，仅需关注其失效率增长情况是否超过阈值。

1）当th＜t＜tl时，设备属于退役观察期，设在此区间的斜率阈值为Kset1。当满足式（22）时，设备可选择退役或缩短巡视周期。

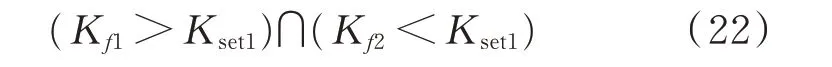
当满足式（23）时，设备可选择退役。

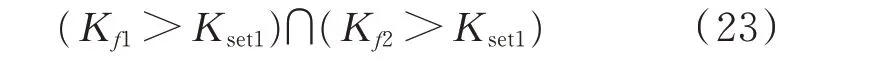
此阶段为退役观察期，退役指标可适当严格选择，即Kset1取值较大，例如可取为0.007。

2）当t＞tl时，设备属于退役期，设在此区间的斜率阈值为Kset2。当满足式（24）时，设备可选择退役或再次缩短巡视周期。

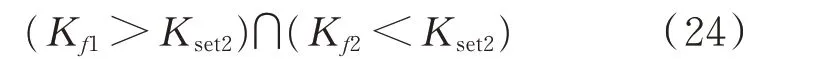
当满足式（24）时，设备可选择退役。

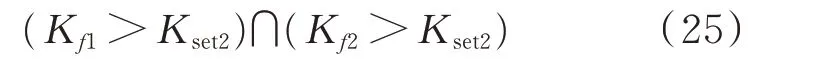
此阶段为退役期，退役指标可适当宽松选择，即Kset2取值较小，例如可取为0.005。

上述退役决策指标取值可根据各电网企业自身实际，并结合一次电网电气设备改造等因素综合决策，具有现实可操作性。

综上所述，从带状失效率模型建立到弹性运维退役策略制定的整体流程如图5 所示。

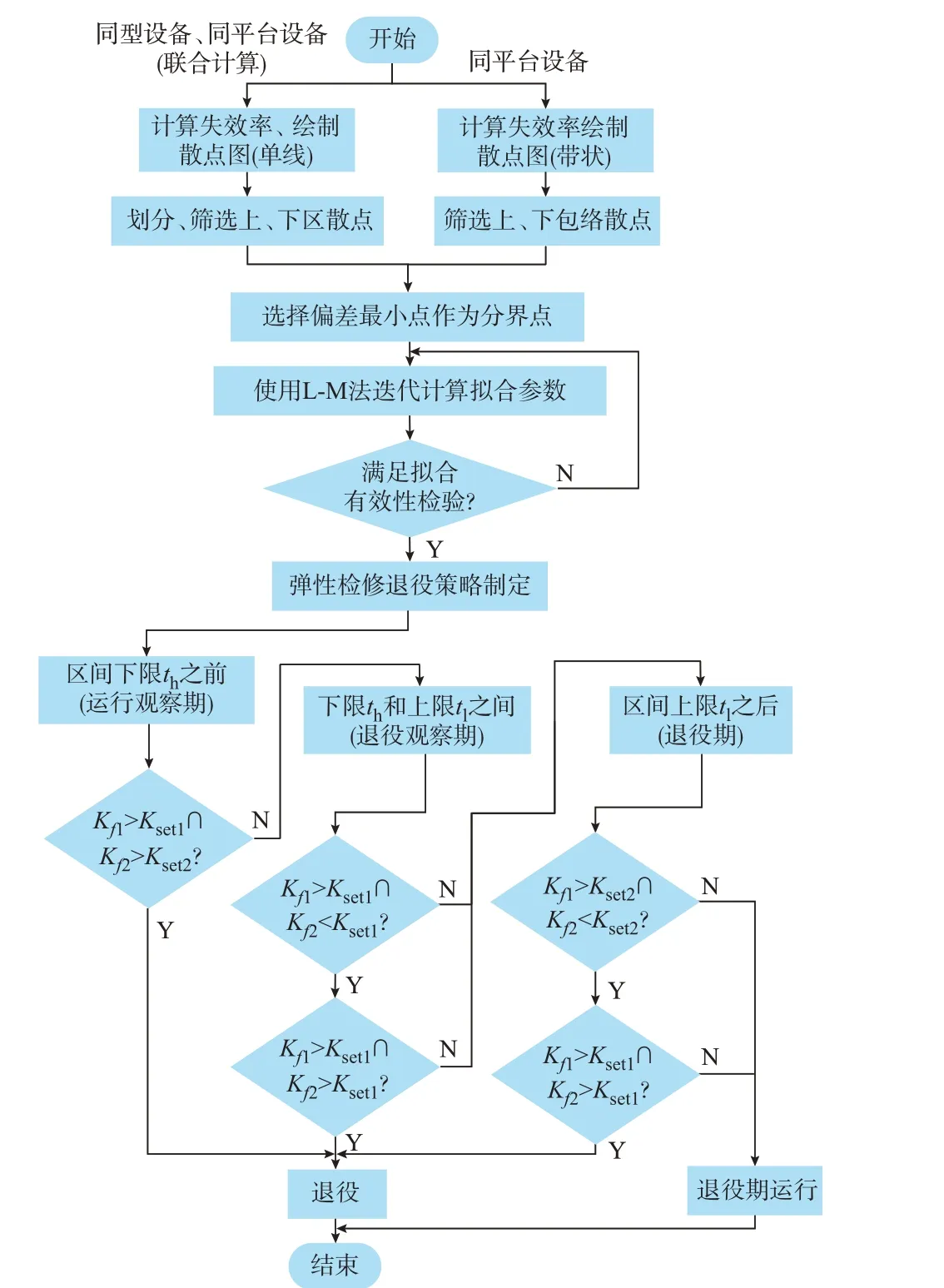
图5 退役策略制定流程图Fig.5 Flow chart of decommissioning strategy formulation

4 案例分析

4.1 寿命模型建立实例

以中国西北某省级电网运行数据为样本，对本文所提方法的有效性进行验证。计算过程中，设定检测年限间隔为0.5 a，不足0.5 a 则按0.5 a 计算。

调取该省级电网某调度单位的某型号保护装置从2016 年至2019 年的失效数据，统计其失效率，绘制失效率散点并用折线连接如图6（a）所示，以此作为同型设备的失效率数据样本，拟合的带状失效区域如图6（b）所示。

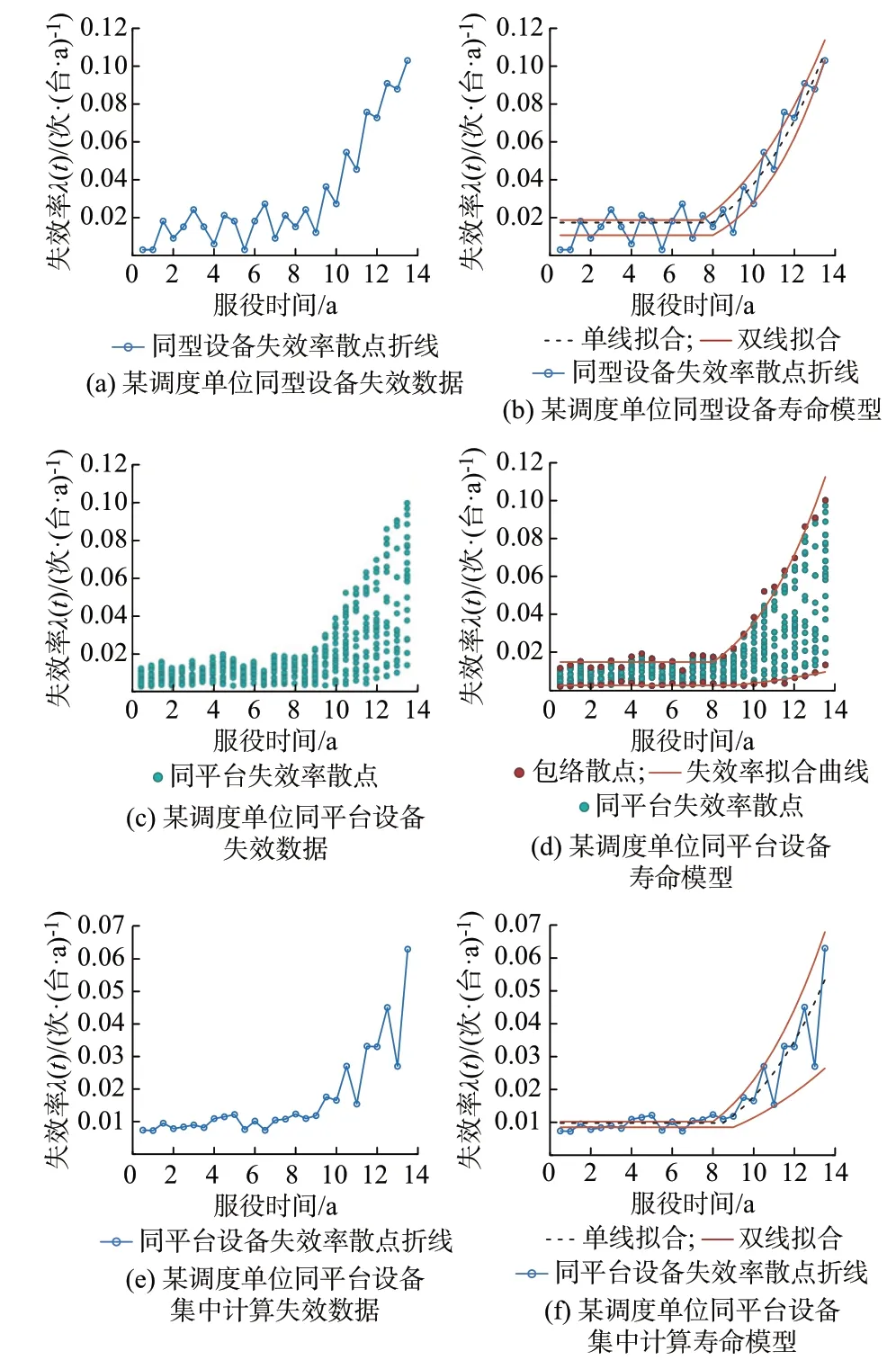
图6 同型和同平台设备的失效数据和寿命模型Fig.6 Failure data and life models for equipment of the same type and platform

对同平台设备的算例则采用下述2 种方法比较其结果:

方法1:同平台设备失效率散点带状法。即调取同调度单位“某保护设备制造企业”中2016 年至2019 年硬件平台相一致的线路保护、母线保护等，共计22 种型号装置进行失效情况统计，绘制失效率散点如图6（c）所示，以此作为同平台设备的失效率数据样本，拟合的带状失效区域如图6（d）所示。

方法2:同平台设备失效率累加带状法。即对该调度单位“某保护设备制造企业”中2016 年至2019 年硬件平台相一致的线路保护、母线保护等共计22 种型号装置的失效率进行相加如图6（e）所示，形成单一失效率曲线后再拟合其带状区域结果如图6（f）所示。

对不同分界点的误差值计算结果如表1 所示。表中，曲线1、2 为同型设备失效率的上、下拟合线，曲线3、4 为同平台设备散点失效率上、下拟合线，曲线5、6 为同平台设备集中计算的失效率上、下拟合线，由此选定最佳的分界年限，已在表中加粗显示。

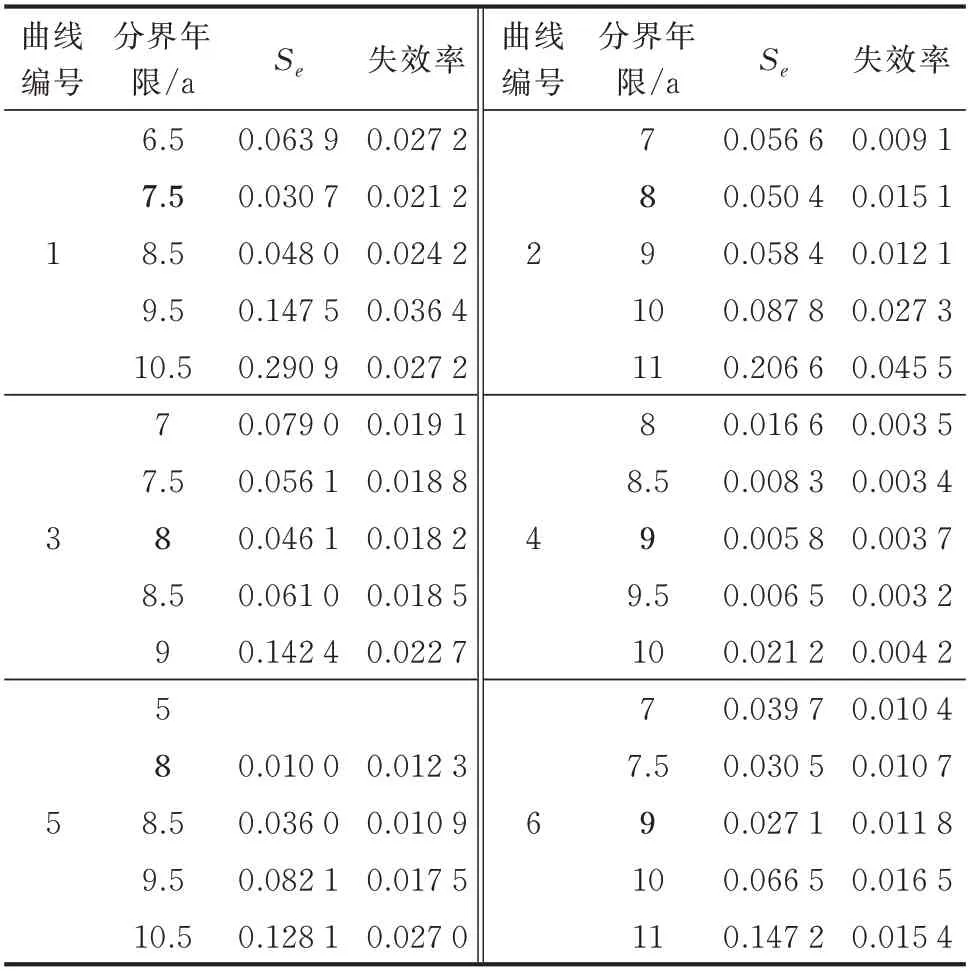
表1 分界年限的误差计算Table 1 Error calculation of dividing years

由表1 可以看到，同型设备上拟合线的最佳分界年限为7.5 a，而同型设备下拟合线的最佳分界年限为8.0 a；对同平台设备，两种拟合方式其分界年限接近，即上拟合线的最佳分界年限为8.0 a，下拟合线的最佳分界年限为9.0 a，其拟合参数如表2 所示，表2 中曲线编号与表1 一致。

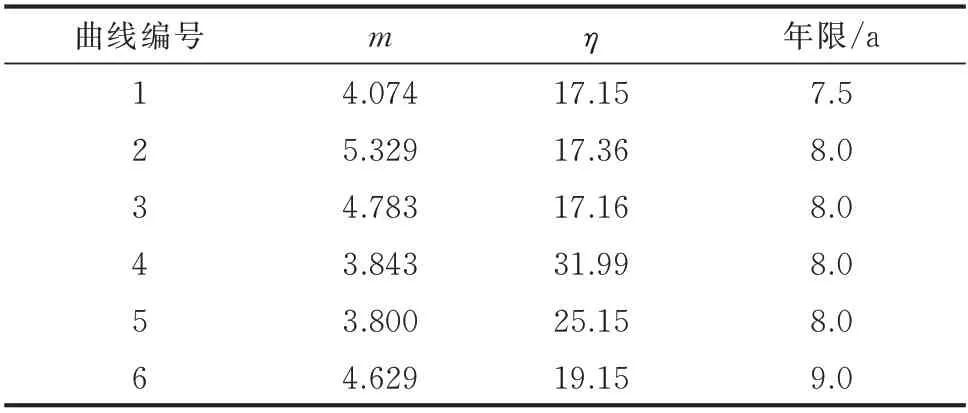
表2 拟合参数Table 2 Parameters of fitting

根据上述拟合结果，可知该型号设备的退役关注区间为7.5～8.0 a；该“保护设备制造企业”系列同平台设备的退役关注区间为8.0～9.0 a。

4.2 弹性退役策略制定实例

以中国西北某省级电网中某调度单位中某同型设备的实际失效数据和某同平台系列设备集中计算的失效数据（如表3 和表4 所示）为例，判断其实际推荐退役年限。按文中所述计算模型计算得到同型设备的退役关注区间下限为7.5 a，同平台系列设备的退役区间下限为8.0 a。对退役关注区后续年限（即老化失效区）的失效曲线拟合结果见表5、表6。

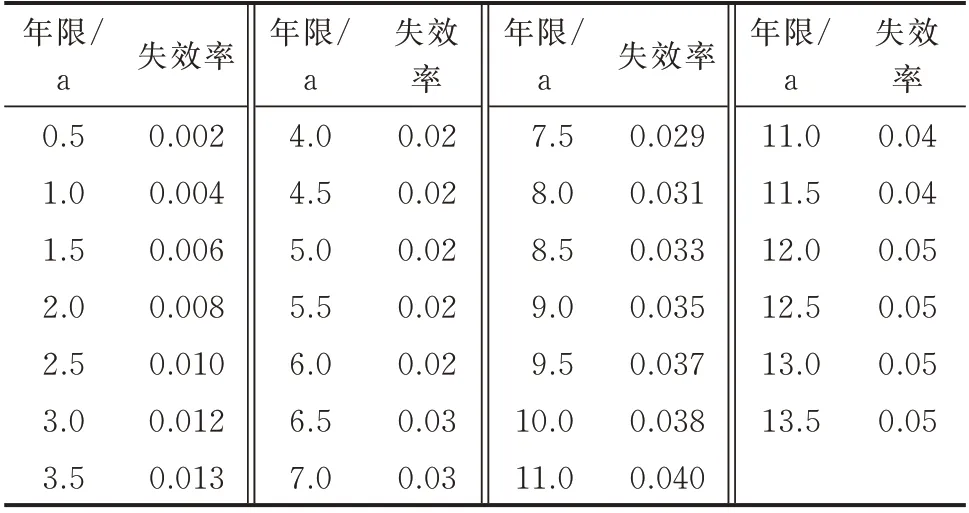
表3 某同型设备的失效率Table 3 Failure rates of the same type of equipment

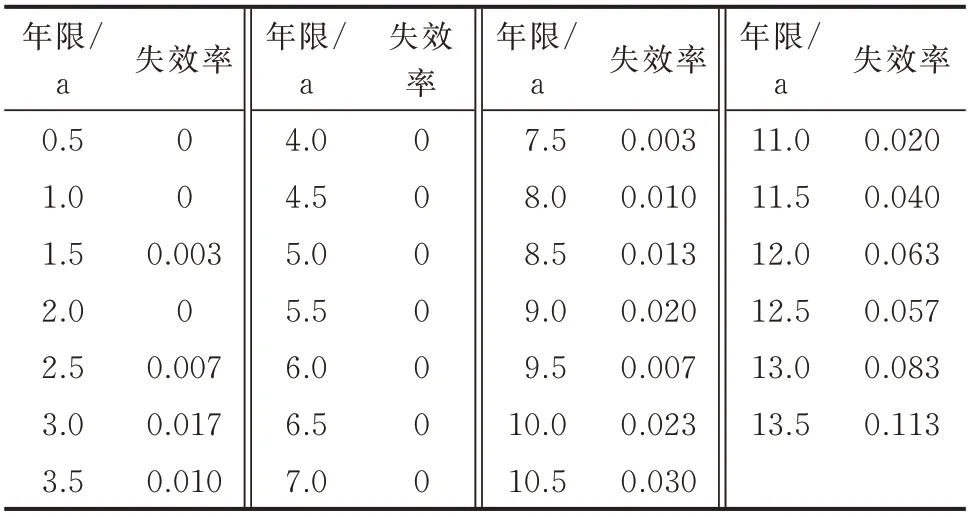
表4 某同平台系列设备集中计算的失效率Table 4 Failure rates by centralized calculation of a series of equipment of the same platform

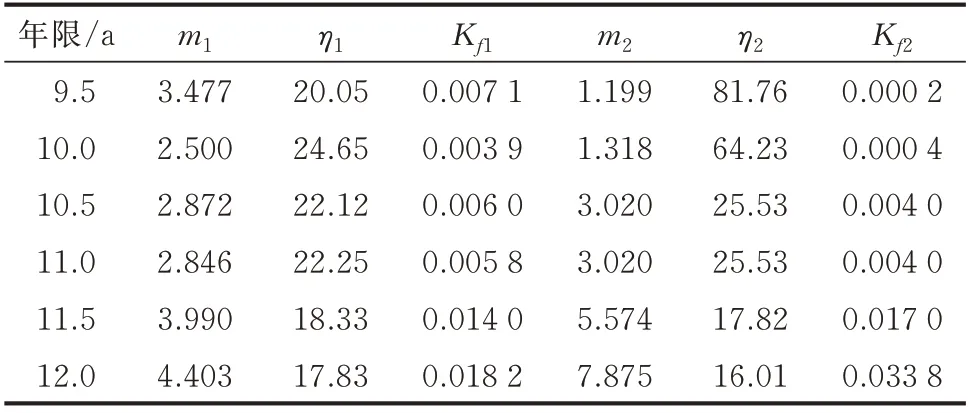
表5 同型设备老化失效区拟合斜率变化Table 5 Fitting slope change of aging failure zone of the same type of equipment

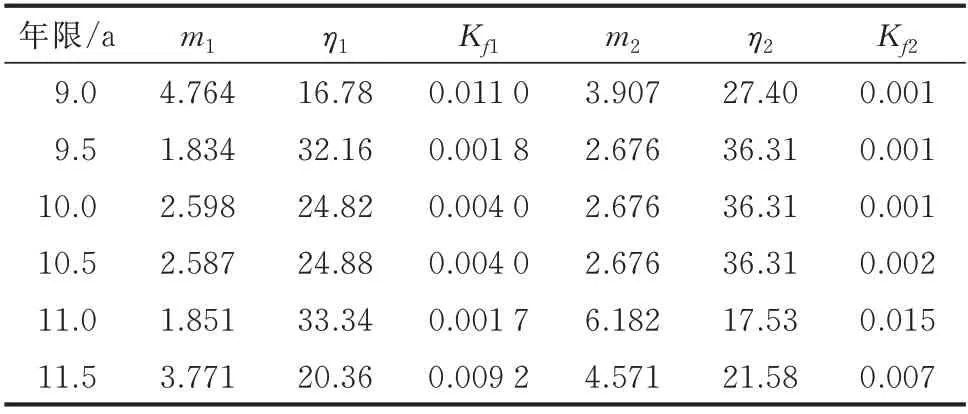
表6 同平台设备老化失效区拟合斜率变化Table 6 Fitting slope change of aging failure zone of equipment of the same platform

当设定Kset1为0.007、Kset2为0.005 时可计算得到实际推荐退役年限。与阈值相比较，根据某调度单位中同型设备的实际情况制定的弹性退役策略建议在9.5 a 时开始考虑退役，在11.5 a 时基本完成退役；根据同平台系列设备的实际情况制定的弹性退役策略建议在9.0 a 时开始考虑退役，在11.0 a 时基本完成退役。

目前，运行部门的该型号设备实际退役年限为10.5 a，该平台系列大部分设备的退役年限为10.0 a。两种类型设备的实际退役时间均在此区间内，与本文模型计算结果基本一致。

5 结语

针对现有继电保护装置失效样本数不足可能导致的数据波动较大和寿命评估与退役决策困难的问题，提出了将传统单线浴盆曲线拟合寿命曲线的模型改变为采用双包络线拟合的区间寿命模型，由此可将保护装置退役时间点选择改为退役时间区间决策。这种处理方法可在样本数据波动较大的情况下仍能做出较为准确的退役决策，为继电保护装置的寿命评估及退役决策提供了一种新的方法。

1）实际数据统计分析表明，继电保护设备的失效主要由硬件缺陷引起。为此，将继电保护寿命评估对象分为了同型设备和同平台设备，由此可开展跨区域保护设备寿命分析和建模，扩展了保护装置样本数量，对失效数据的整体统计特征和个体特征都能有很好的体现。

2）针对保护装置失效率数据的样本质量差异及可靠性差异，提出将保护装置失效率数据分为上下两个数据集，并分别针对上下数据集进行上下包络线拟合，由此得到由上下包络线包围的保护装置失效区间，从而较为准确地反映保护装置群体的失效变化规律。

3）建立的基于Weibull 函数的包络线拟合以及L-M 法拟合求解方法能方便地用于保护装置带状寿命模型建模，在拟合过程快速收敛的同时能获得最优解。算例验证了拟合的有效性。

4）利用建立的带状寿命模型，可得到保护装置退役的时间区间，灵活用于退役决策，为状态检修、技改以及更换等提供参考依据。

5）本方法还对其他工业设备的寿命模型建模提供参考，适用于样本数据波动较大的情况，能较好地解决实际工程中的设备运维决策问题。

由于模型预测的整体准确程度不仅与输入模型的失效率准确程度呈正相关，还与装置插件更换引起的役龄回退等因素有关，本文模型尚未对输入数据的有效性进行辨识，也暂未计及役龄回退对模型的修正，后续研究中将进一步研究保护装置运行过程中不良数据的剔除以及保护装置插件可靠性对整体可靠性的影响等问题，从而更准确地建立保护装置的寿命模型。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。