V/f控制下柔性直流换流器阻抗建模及中高频谐振特性分析

冯俊杰，傅 闯，邹常跃，赵晓斌，陈 威，许树楷

（1. 直流输电技术国家重点实验室（中国南方电网科学研究院有限责任公司），广东省广州市 510663；2. 中国南方电网有限责任公司，广东省广州市 510663）

0 引言

近年来，基于模块化多电平换流器（modular multilevel converter，MMC）的柔性直流输电技术已被大量运用于国内外风电并网工程中［1-2］。然而，由于风机换流器与柔性直流换流器均为具有宽频响应特性的电力电子装置，风电场经柔性直流送出时，二者存在相互作用。当阻抗匹配不当时，易引发谐振不稳定问题，这也成为了制约柔性直流输电系统风电送出能力的主要因素之一［3-6］。例如，德国北海Borwin1 海上风电柔性直流送出工程和中国南澳风电柔性直流送出工程在运行或调试过程中均发生过谐波谐振现象［7-8］。

不同应用场景下，柔性直流换流器所采取的控制策略不同，当其接入风电场等无源系统时，须采用定交流侧电压控制策略，即V/f控制以维持稳定的并网点电压幅值和频率［9-10］。因此，其阻抗特性与接入交流大电网应用场景下的柔性直流换流器有所差异。为将阻抗分析法［11-13］运用于风电场柔性直流送出系统谐振特性分析中，首先需要建立V/f控制下柔性直流换流器的等效阻抗。

文献［14-16］针对交流电压单环控制的MMC，建立了其等效阻抗模型，并分析了风电场柔性直流送出系统的谐振特性，但其研究结论不适用于常用的双闭环矢量控制。文献［17-19］建立了双闭环定交流电压控制的MMC 频率耦合正负序阻抗模型，可实现双闭环对风电场柔性直流送出系统谐振稳定性的影响的特性分析，但忽略了电压前馈或控制链路延时等因素的影响。文献［20］进一步考虑对侧换流站和直流电缆的影响，发现直流侧动态特性将会对柔性直流换流器的低频段阻抗特性产生影响。以上分析均主要针对次/超同步或低频振荡问题，对V/f控制下的柔性直流换流器进行阻抗建模，较少关注换流器的中高频阻抗特性。同时，忽略了电压前馈、交流电压电流正负序分离控制和控制系统链路延时等因素的影响，该环节正是影响换流器中高频阻抗特性的重要因素［21］。

近年来，在中国柔性直流输电工程接入交流大电网或风电场的应用场景中，均发生过多起高频谐振事件，如2017 年4 月鲁西背靠背直流工程发生 了1 270 Hz 左右的谐波谐振［22］；2018 年12 月渝鄂背靠背工程南通道发生了1 810 Hz 和700 Hz 左右的高频谐振［23］；2021 年10 月如东海上风电柔性直流送出工程在调试过程中观察到2 000 Hz 和2 500 Hz左右的高频振荡。文献［21-25］针对柔性直流接入交流大电网的高频谐振问题开展了深入研究，并提出了加入电压前馈低通滤波器、减小系统链路延时、减小电流内环比例-积分（PI）控制器比例系数等抑制措施，但是上述抑制措施并不一定适用于V/f控制下的柔性直流换流器。同时，近年来海上风电柔性直流送出系统逐渐开始采用风电场侧66 kV 交流汇集方案，如正在规划建设中的Borwin5、Dogger bank、青洲五七海上风电接入项目等。该方案取消了海上升压变压器，风电场侧感性特性降低、容性特性增强，加大了系统发生中高频谐振的风险。因此，针对V/f控制下的柔性直流输电系统，开展中高频谐振特性分析显得尤为重要，可为保证风电柔性直流送出系统的稳定运行奠定基础。

综上，本文考虑正负序交流电压外环、电流内环、电压前馈、系统调制和链路延时等因素，建立了柔性直流换流器的正负序阻抗模型；分析了换流器中高频阻抗特性的主要影响因素，并提出了相应的阻抗重塑措施；以66 kV 交流汇集的海上风电柔性直流送出系统为例，开展了中高频谐振特性分析；最后，在PSCAD/EMTDC 中搭建了电磁暂态仿真模型，验证了中高频谐振特性分析的正确性以及阻抗重塑措施的有效性。

1V/f控制下柔性直流换流器控制系统结构

V/f控制下柔性直流换流器控制系统结构如图1 所示，采用正负序交流电压外环、电流内环的双闭环控制结构。与连接有源电网下的控制方式不同，定交流侧电压控制中坐标变换的角度直接给定为θ1=ω1t，其中ω1为基波角频率，因此，可将并网点电压频率控制在额定频率。正序交流侧电压外环控制量分别为母线d轴正序电压udP和q轴正序电压uqP，给定正序交流侧电压参考值UrefdP等于母线电压幅值且UrefqP为零，保持交流侧母线电压幅值和频率稳定，通过正序交流电压外环控制生成电流内环正序d轴电流参考值irefdP和q轴电流参考值irefqP。负序交流侧电压外环控制量分别为母线d轴负序电压udN和q轴负序电压uqN，给定负序交流侧电压参考值UrefdN、UrefqN均为零，通过负序交流电压外环控制生成电流内环负序d轴电流参考值irefdN和q轴电流参考值irefqN。

图1 中:u和i分别为交流侧电压和电流；下标d、q分别表示d、q轴分量；下标A、B、C 分别表示A、B、C 三相；下标P、N 分别表示正、负序分量；上标ref表示参考值；Gsd为1/4 工频周期延时滤波环节传递函数且Gsd=0.5(1+e-sT/4)，其中T为电网电压工频周期；Kd为电流内环解耦系数；Gsv和Gsi分别为电压采样和电流采样环节传递函数；Gd为系统调制与链路延时传递函数；Gfv为电压前馈低通滤波器传递函数。

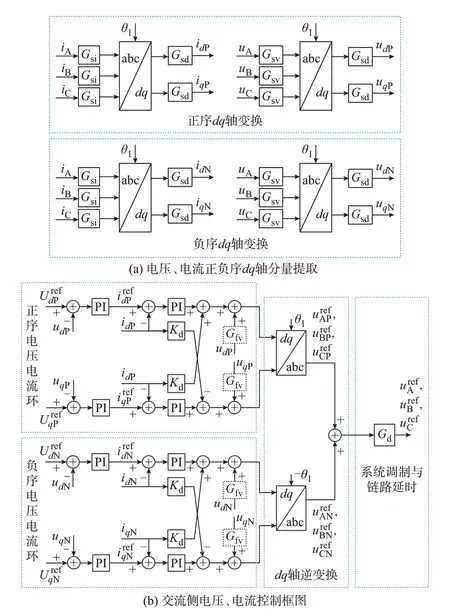
图1 柔性直流换流器控制系统框图Fig.1 Block diagram of flexible DC converter control system

2V/f控制下柔性直流换流器等效阻抗模型

本文采用谐波线性化的方法对V/f控制下的柔性直流换流器进行建模。考虑正负序小扰动后，并网点电压、电流的时域和频域表达式分析如下。

2.1 abc/dq轴正变换

2.1.1 正序分量abc/dq变换

坐标变换的角度直接给定为θ1=ω1t，结合正序电压时域表达式，考虑采样环节和正负序分离中的1/4 工频周期延时滤波器，得到交流电压dq轴分量的正序频域表达式为:

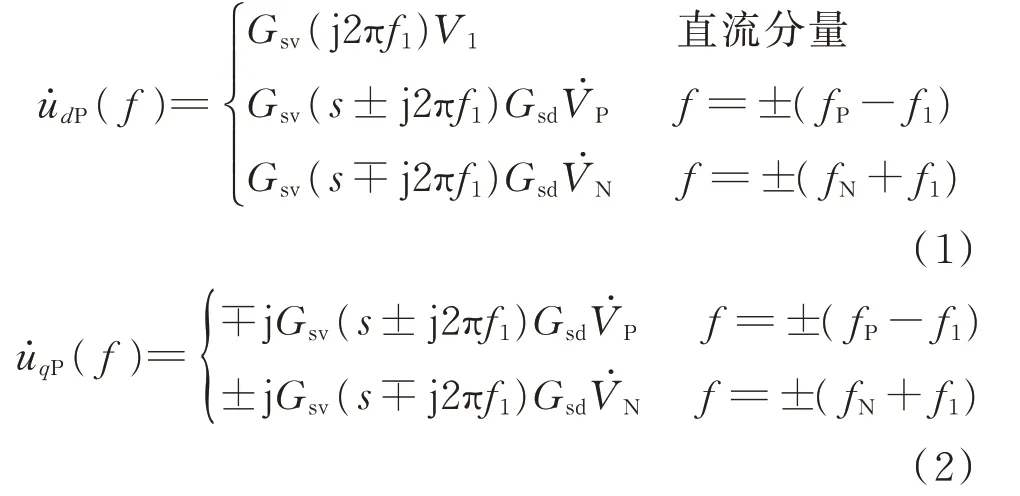
式中:f1、fP、fN分别为基波频率、正序扰动频率和负序 扰 动 频 率；V1为 交 流 电 压 基 波 幅 值；V˙P和V˙N分别为交流电压正、负序扰动分量。

同理，得到交流电流dq轴分量的正序频域表达式为:

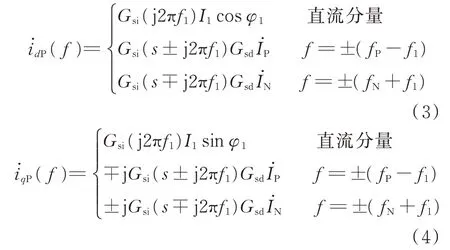
式中:I1为电流基波分量幅值；φ1为基波电流的相角；I˙P和I˙N分 别为交流 电流正、负序扰动 分量。

2.1.2 负序分量abc/dq变换

负序分量abc/dq轴变换中，坐标变换的角度为-θ1。正序基波分量以角度-θ1为基准进行坐标变换后表现为两倍频的形式，由于1/4 工频周期延时滤波器在两倍频处增益为零，可以不再考虑两倍频分量。因此，交流电压dq轴负序分量仅含扰动分量:

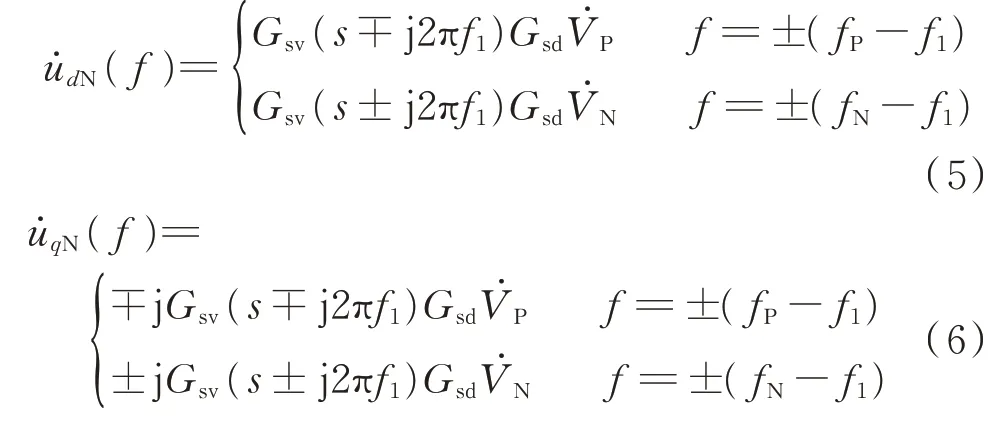
同理，交流电流dq轴负序分量可以写成类似的形式。

2.2 正序交流电压外环和电流内环建模

由图1（b）得到正序电流内环dq轴参考值为:

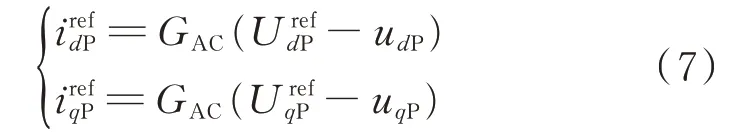
式中:GAC为交流电压外环PI 控制器传递函数。

将正序dq轴电压频域表达式代入式（7）得到正序电流内环dq轴参考值的小信号表达式。

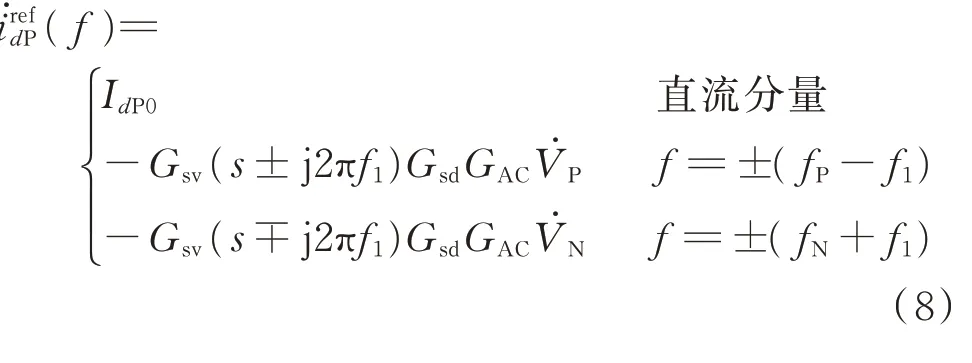
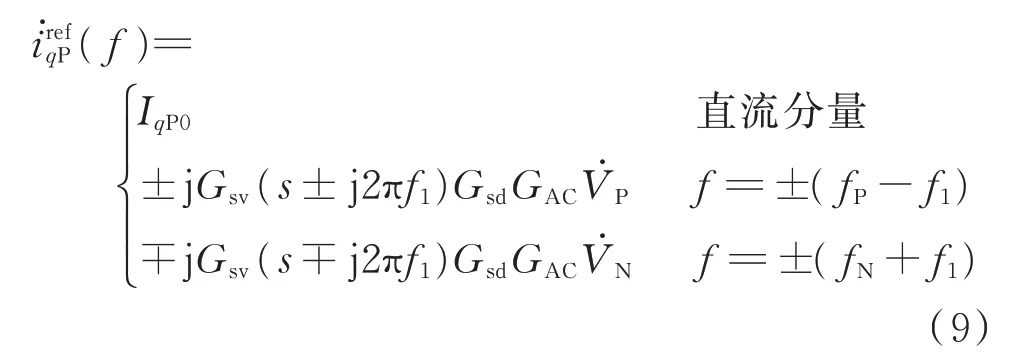
式中:IdP0和IqP0分别为稳态情况下正序d、q轴电压控制环的输出值。

由图1（b）得到正序电流内环输出为:

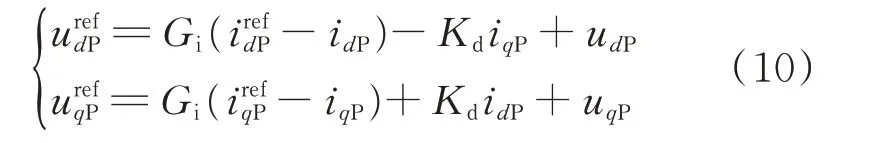
式中:Gi为电流内环PI 控制器传递函数。

为了提高可读性，推导过程中不列写电压、电流采样环节的传递函数，将交流电压环输出及正序dq轴电压、电流频域表达式代入式（10），得到正序dq轴调制参考电压的表达式为:

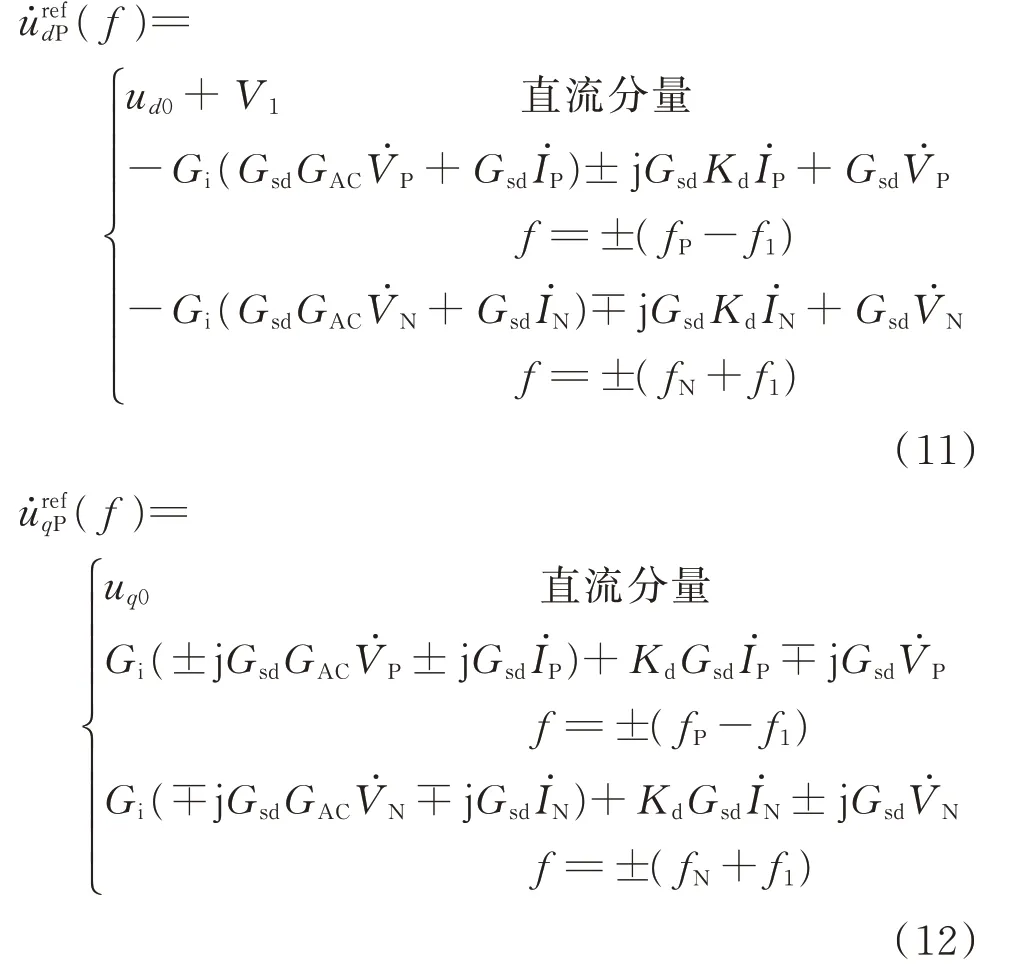
式中:ud0和uq0分别为d、q轴电流控制器的稳态输出值。

2.3 负序交流电压外环和电流内环建模

与正序交流电压外环的推导过程类似，由图1（b）得到负序电流内环dq轴参考值的小信号为:

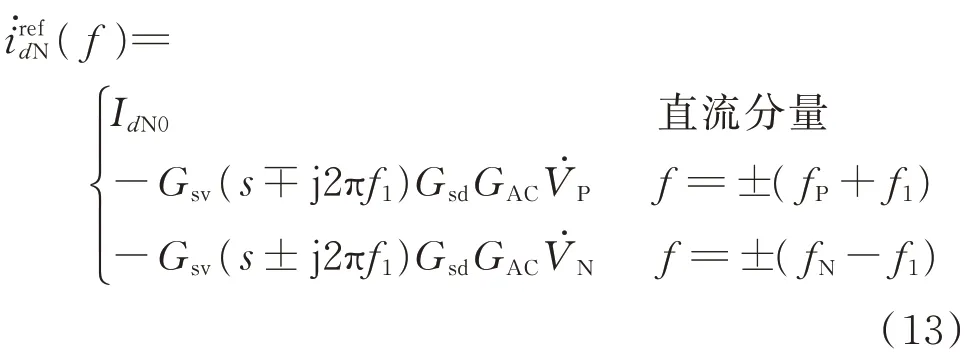
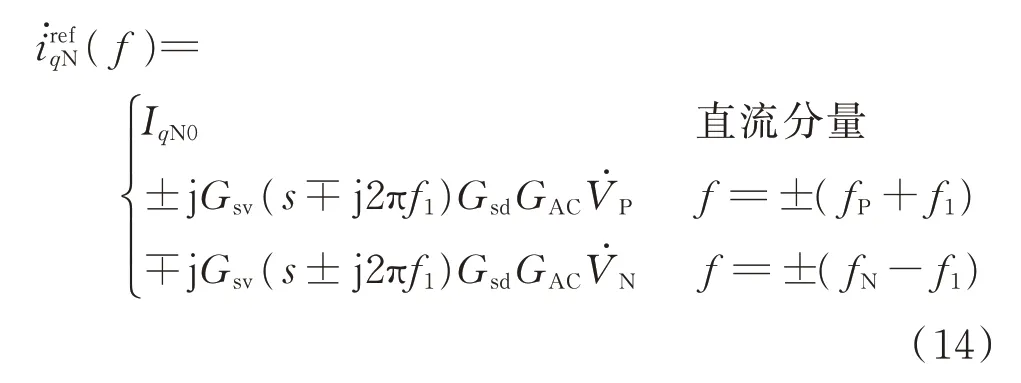
式中:IdN0和IqN0分别为稳态情况下负序d、q轴电压控制环的输出值。

考虑到负序电流控制器稳态输出为零，即没有直流分量，进一步得到正序dq轴调制参考电压为:

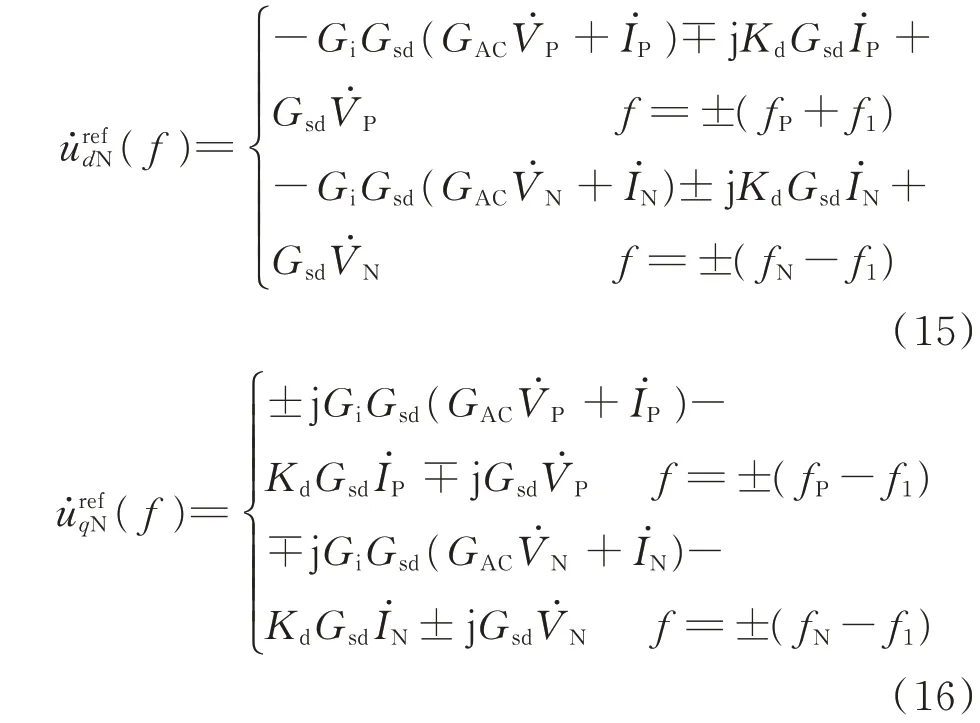
2.4dq/abc 轴逆变换

电流控制器输出经dq/abc 轴逆变换可得到三相静止坐标系下的调制参考电压，由式（11）、式（12）得到正序电压A 相调制波小信号为:

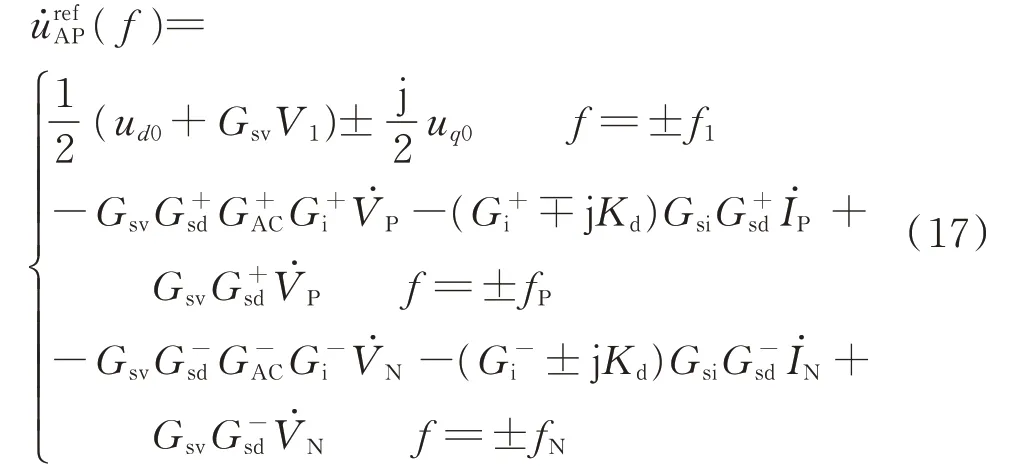
式中:上标“+”“-”表示不同的频率偏移，即G+=G(s-jω1)，G-=G(s+jω1)。

负序分量dq轴逆变换的参考角度为-θ1，则负序电流控制器在静止坐标系下的A 相电压输出结果为:

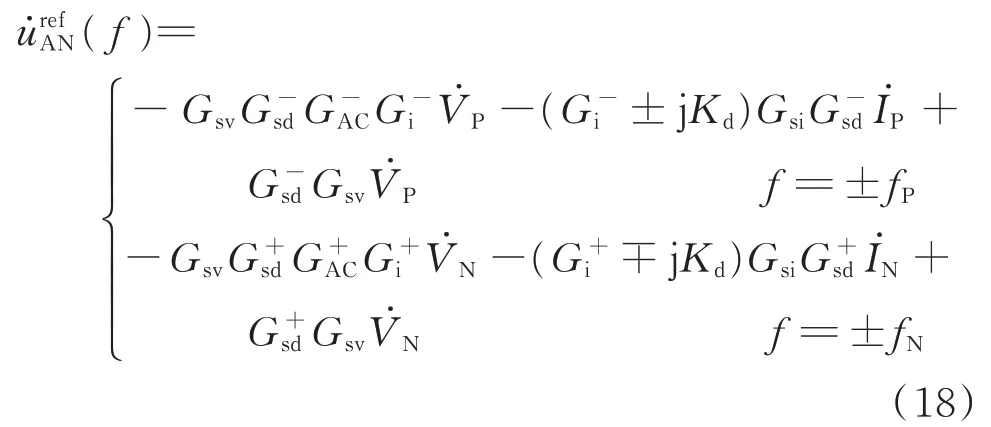
将式（17）与式（18）相加，即可得到正负序独立控制的总输出表达式urefA。

2.5V/f控制下柔性直流换流器正负序等效阻抗模型

仍以A 相为例对V/f控制下的柔性直流换流器正负序阻抗进行推导。由于MMC 控制器采用离散控制，分析过程中将离散控制等效为零阶保持器。因此，计及调制作用和系统链路延时作用的传递函数表示为:

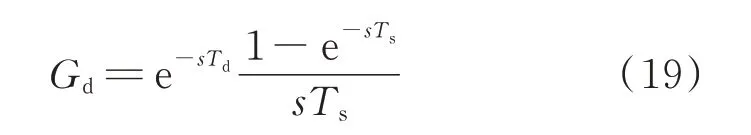
式中:Td为控制系统链路延时；Ts为控制周期。

A 相输出电压为:

式中:L为换流器交流侧等效电感。

当f=fP时，将式（17）至式（20）代入式（21），得到V/f控制下柔性直流换流器正序阻抗表达式为:

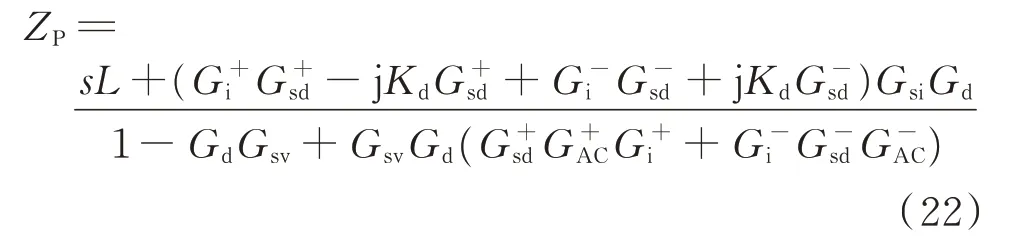
同理，当f=fN时，得到负序阻抗表达式为:

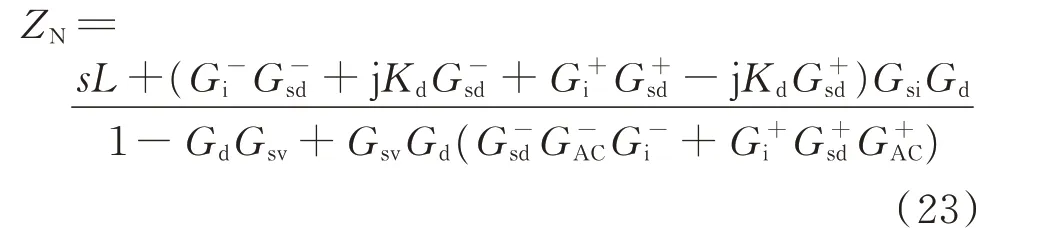
3V/f控制下柔性直流换流器中高频阻抗特性分析

为了便于分析各控制环节对柔性直流换流器中高频阻抗特性的影响，将正负序阻抗写成模块的形式:

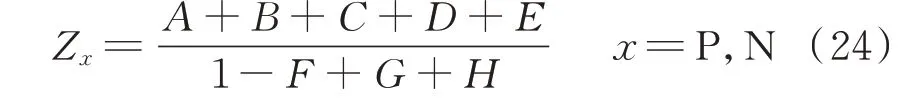
其中，不同字母表示不同的影响因素，各字母所代表的环节及具体表达式如表1 所示。当加入电压前馈低通滤波器时，扰动项F则变换成GdGsvGfv。

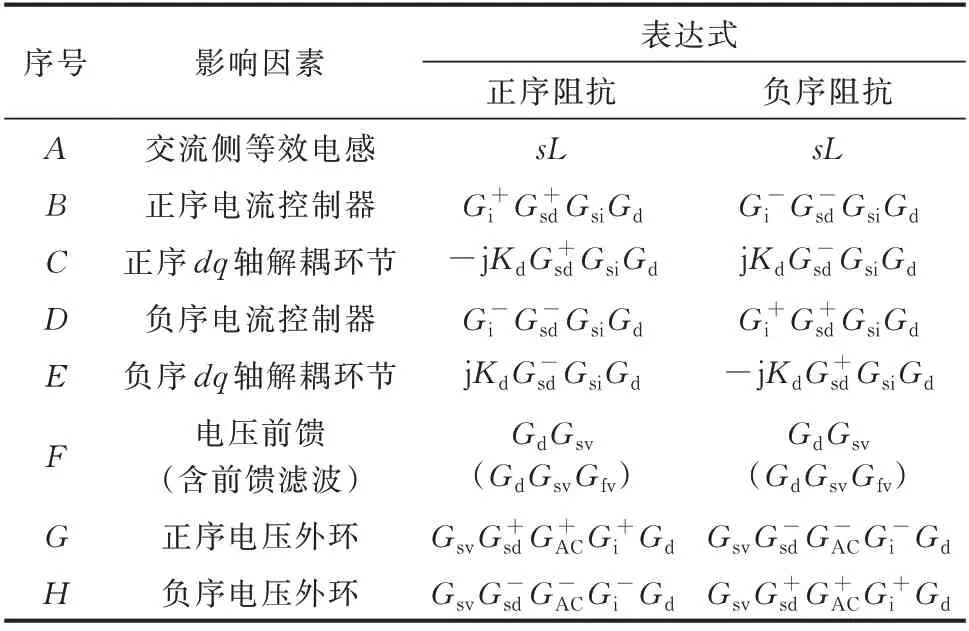
表1 换流器等效阻抗影响因素Table 1 Influence factors of converter equivalent impedance

当不考虑某些控制环节的影响时，可将B项至H项中相应控制环节的表达式置0；当不考虑采样环节，如电压采样环节、电流采样环节的影响时，可将相应的传递函数Gsv、Gsi置1；当不考虑滤波器，如电压前馈低通滤波器、1/4 工频周期延时滤波器等的影响时，可将相应的传递函数Gfv、Gsd置1。采样环节采用延时等效，即Gsv=e-sTdv、Gsi=e-sTdi，其中Tdv和Tdi分别为电压采样和电流采样延时。给定标幺值下系统参数如附录A 表A1 所示，对换流器等效阻抗特性进行分析。

3.1 电流内环对阻抗特性的影响

当仅考虑电流内环的影响时，将式（24）中的G项和H项置0，得到换流器正负序阻抗表达式为:

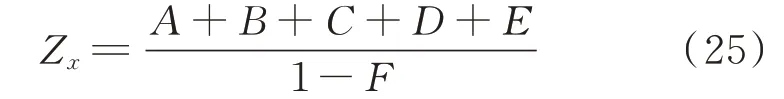
由式（25）得到换流器等效阻抗的频率特性曲线如附录A 图A1 所示。可见换流器阻抗存在两处谐振点，并伴随着宽频带的高频负阻尼特性。其主要原因为:电压前馈把延时项引入阻抗表达式的分母中，使得分母为1-GdGsv。由于零阶保持器可近似等效为1/2 周期延时，电压前馈引入的扰动项F可写为:

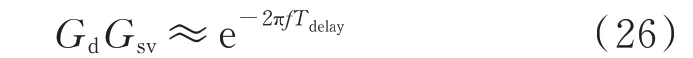
式中:Tdelay为系统总延时，Tdelay=Td+Tdv+Ts/2。GdGsv在-1 到1 范围内呈周期性变化，当f≈k/Tdelay（k为非零正整数）时，GdGsv≈1，换流器阻抗的分母1-GdGsv≈0，使得换流器阻抗在高频段出现谐振点并伴随着负阻尼特性。在附录A表A1 给定参数下，谐振点对应的频率约为2 200 Hz、4 400 Hz。

在实际工程中，通常采用在电压前馈加入低通滤波器的方式对高频谐振点和负阻尼特性进行抑制［21，23］。由于文献［21］已对电流内环中各环节对换流器阻抗的影响特性进行了分析，本文不再对电流内环其他因素的影响进行赘述，主要关注定交流侧电压控制对换流器阻抗特性的影响。

3.2 正序交流电压外环对阻抗特性的影响

在3.1 节的基础上，进一步考虑正序交流电压外环的影响，得到换流器的正负序阻抗表达式为:

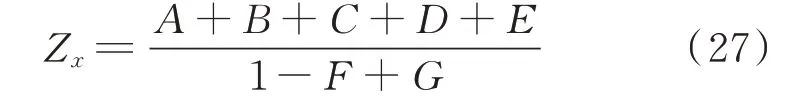
正序交流电压外环引入的扰动项G体现在阻抗表达式的分母中，扰动项包含电压外环传递函数、电流内环传递函数、采样环节、系统延时与调制环节、1/4 工频周期延时滤波器。根据式（27）绘制正负序阻抗特性曲线如图2 所示。由图2 可知，加入正序交流电压外环后换流器阻抗曲线出现了严重的中低频振荡，振荡周期约为200 Hz，其中阻抗幅值越大，振荡幅度越大。对比正负序阻抗曲线，二者阻抗特性相近、振荡周期相同，但谐振峰值频率相差约100 Hz，为振荡周期的1/2。

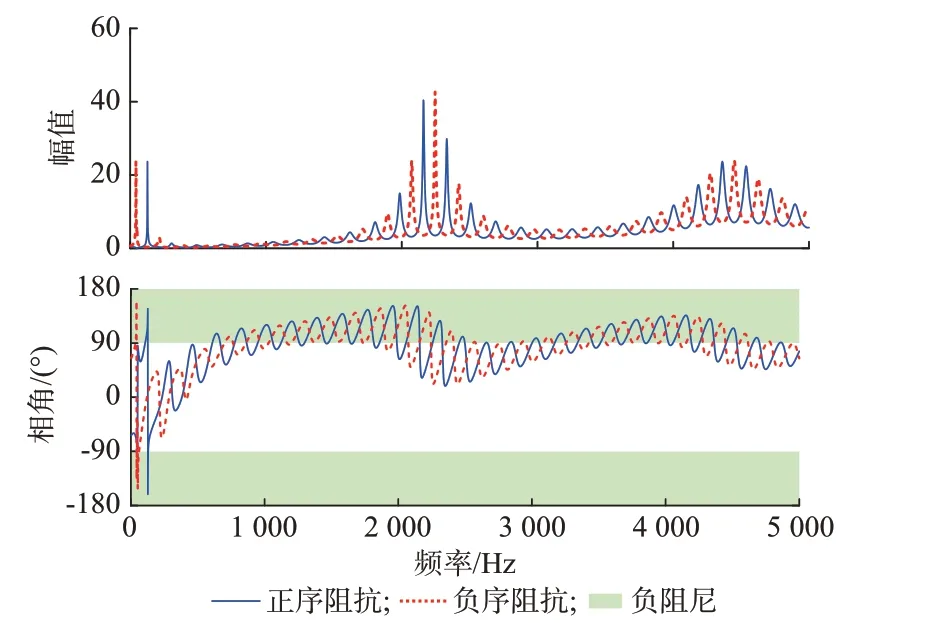
图2 正序交流电压外环对换流器阻抗特性的影响Fig.2 Influence of positive sequence AC voltage outer loop on impedance characteristics of converter

式（28）中，GsvGd和Gsd均为呈周期变化的传递函数，其中GsvGd变化周期由式（26）决定，在附录A表A1 给定参数下振荡周期约为2 200 Hz，Gsd变化周期约为200 Hz。由此可见，换流器阻抗特性曲线的低频周期性振荡主要由正负序分离中的1/4 工频周期延时滤波器引起。

3.3 负序交流电压外环对阻抗特性的影响

在3.2 节的基础上，进一步考虑负序交流电压外环的影响，得到换流器的正负序阻抗表达式为:

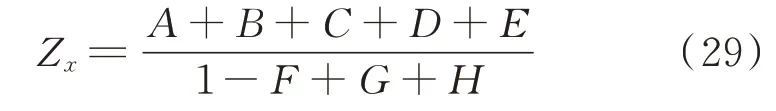
与正序交流电压外环相同，负序交流电压外环引入的扰动项H同样体现在阻抗表达式的分母中。令交流电压外环PI 控制器比例和积分系数分别为0.1、100，绘制正负序阻抗特性曲线如图3 所示。

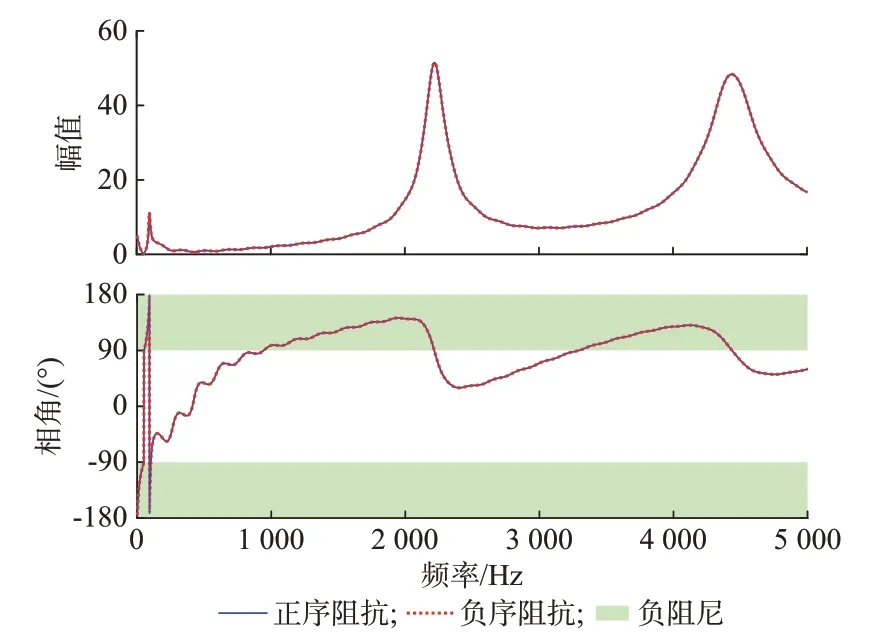
图3 负序交流电压外环对换流器阻抗特性的影响Fig.3 Influence of negative sequence AC voltage outer loop on impedance characteristics of converter

由图3 可知，换流器阻抗频率特性曲线的周期性振荡现象消失，阻抗特性得到改善。其主要原因为加入负序电压外环后，交流电压控制在正负序阻抗中引入的扰动项如式（30）所示。

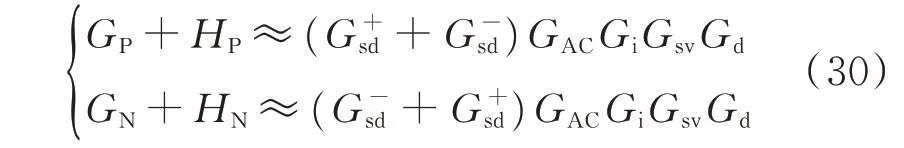
由于G+sd+Gsd=1，加入负序交流电压外环后，交流电压控制引入的扰动项修正为GACGiGsvGd，由1/4 工频周期延时滤波器引入的扰动项被抵消。但换流器阻抗特性曲线在中高频段仍存在2 个谐振峰，负阻尼特性明显，阻抗曲线总体趋势与3.1 节相似，但谐振峰幅值相对较小。

需要说明的是，当负序控制仅采用负序电流控制时，若正序控制中电压外环控制量由正序交流电压改为包含正负零序分量的总电压，可以得到相似的效果。此时换流器正、负序阻抗分别为:

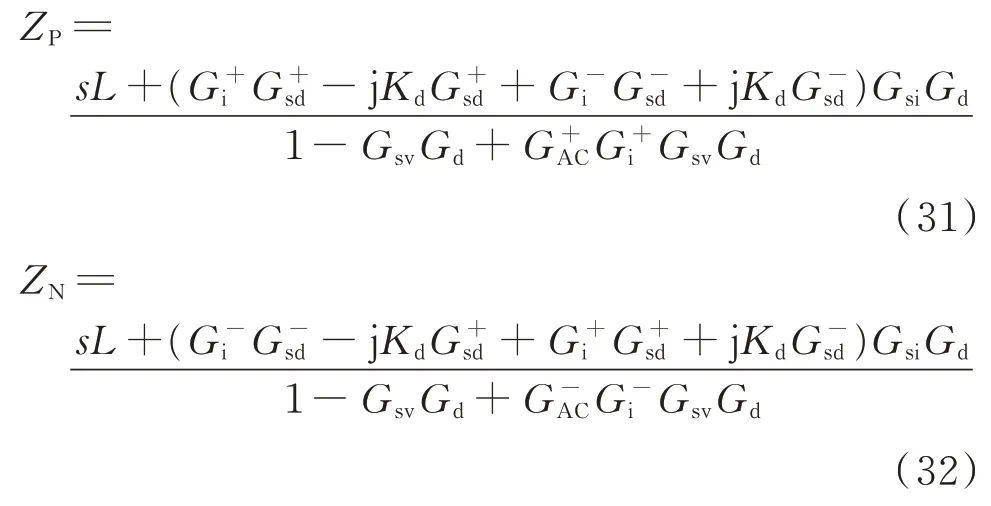
由此可见，为避免阻抗特性出现约200 Hz 的低频振荡，交流电压外环控制量不宜仅为正序电压分量，应同时控制正负序分量，可采取正负序电压分离控制或在正序电压外环中控制交流总电压。

3.4 电压前馈控制方式对阻抗特性的影响

对于接入交流大电网的柔性直流换流器，通常采用定功率控制、定直流侧电压控制，为改善阻抗特性、削减阻抗谐振尖峰，通常在电压前馈环节中加入低通滤波器。为分析该抑制策略在定交流电压控制方式下的有效性，在电压前馈中加入截止频率为200 Hz 的二阶低通滤波器，绘制阻抗特性曲线如附录A 图A2 所示。

由附录A 图A2 可见，加入电压前馈二阶低通滤波器后阻抗曲线的谐振峰和负阻尼特性没有得到抑制。对比3.1 节中的结果，第1 个谐振点频率提前，约为1 100 Hz，对应的第1 段负阻尼频率范围移至中频段，约为400～1 100 Hz，甚至在1 000 Hz 附近出现了容性负阻尼现象，阻抗特性严重恶化。加入电压前馈二阶低通滤波器后，扰动项F在中高频段近似为0，正负序阻抗表达式可简化为:

若在交流电压控制环中加入低通滤波器亦可消除扰动项GACGiGsvGd在中高频段的影响，抑制高频谐振点，但同时也牺牲了系统动态响应性能。

综上，对于V/f控制下的柔性直流换流器，加入电压前馈低通滤波器虽然可以抑制电压前馈的扰动，但是由交流电压控制引入的扰动项扮演了与此前电压前馈相似的作用。因此，加入电压前馈低通滤波器的阻抗改善策略不适用于V/f控制下的柔性直流换流器。

4V/f控制下柔性直流换流器中高频阻抗重塑措施

由上一章分析可知，为改善V/f控制下柔性直流换流器的阻抗特性，须结合电压前馈环节和交流电压控制环节进行协同优化。

由于在中高频段交流电压外环和电流内环PI控制器的积分项近似为0，可将二者PI 控制器的传递函数由比例系数等效。且由于jGsd-jG+sd=e-sT/4、G+sd+Gsd=1，将换流器等效阻抗的表达式简化为:

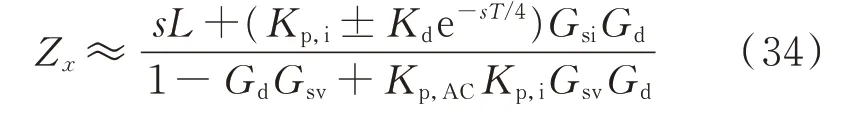
式 中:Kp，AC和Kp，i分 别 为 电 压 外 环 和 电 流 内 环PI 控制器的比例系数。可见，在中高频段当Kp，ACKp，i=1 时，由电压前馈引入的扰动项GsvGd和由交流电压控 制 外 环 引 入 的 扰 动 项Kp，ACKp，iGsvGd可 以 相 互 抵消。令Kp，i=1、Kp，AC=1 得 到 换 流 器 阻 抗 的 频 率特性曲线如图4（a）所示，幅频特性曲线的谐振峰消失，由电压前馈和交流电压控制外环引入的负阻尼特性得到完全抑制。需要说明的是，实际工程中由于控制量均经过了标幺化处理，电压电流环PI 控制器比例系数通常在1 附近取值，在控制参数设计过程中令Kp，ACKp，i=1 实现 难度不大。

然而，由于换流器等效阻抗的分子项仍然存在由电流内环引入的系统延时项GsiGd，图4（a）中换流器等效阻抗在500～1 500 Hz 仍然存在负阻尼特性。由式（34）可知，电流内环PI 控制器比例系数Kp，i的大小与电流内环系统延时项GsiGd作用强度成正比，为了削弱电流内环延时项GsiGd的作用，在保证系 统 动 态 性 能 以 及Kp，ACKi，AC=1 的 前 提 下 应 使 电流内环PI 控制器比例系数尽可能小。令Kp，i=0.5、Kp，AC= 2.0 得到换流器阻抗的频率特性曲线如图4（b）所示，在500～1 500 Hz 内的阻抗的负阻尼特性得到了有效抑制，对比图4（a），减小电流内环PI 控制器比例系数后的阻抗相角更接近90°。

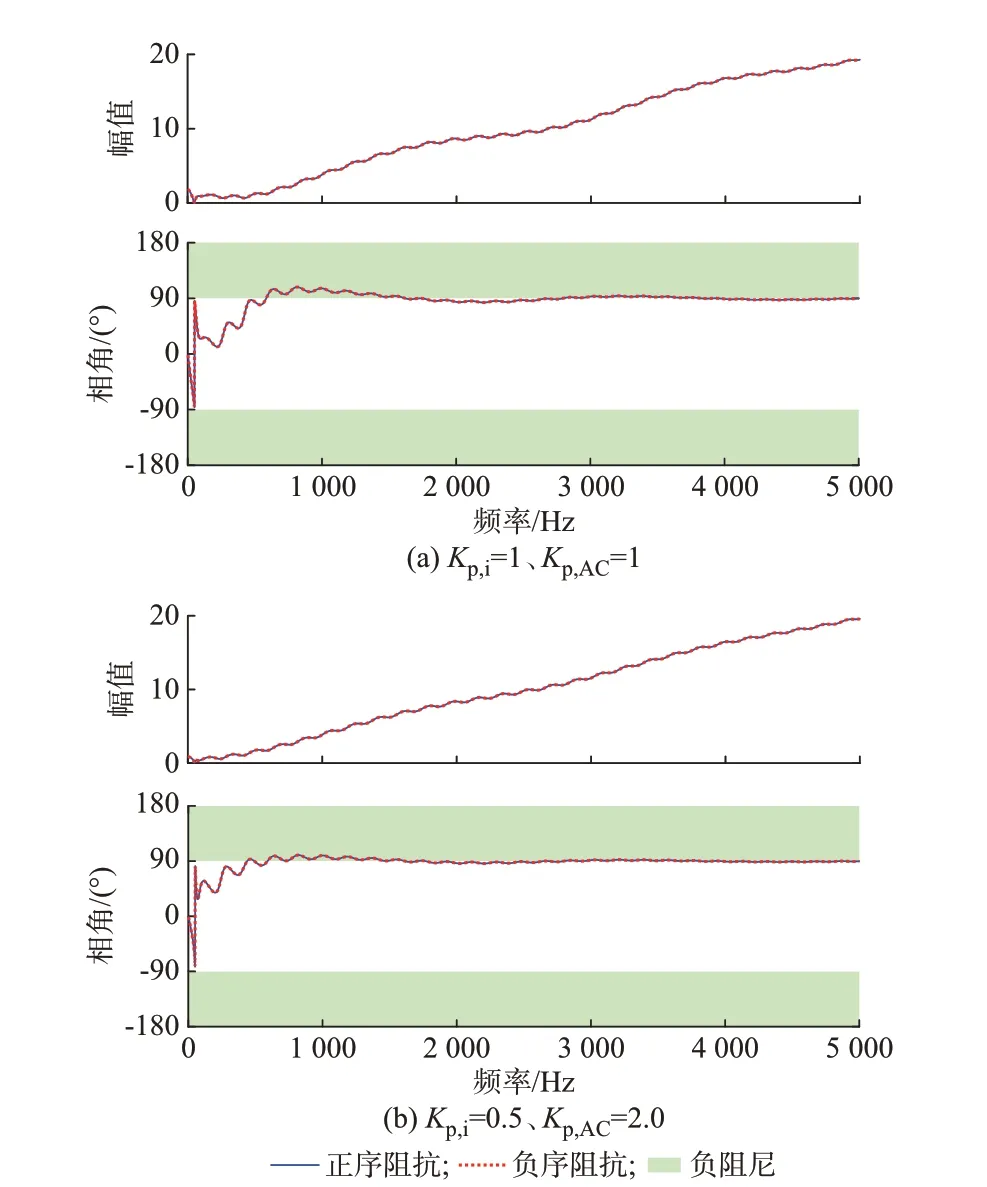
图4 采用改善措施后的阻抗特性曲线Fig.4 Impedance characteristic curves with improvement measures

综上，为改善采用V/f控制下柔性直流换流器的中高频阻抗特性，须满足如下条件:

1）定交流侧电压控制中的控制量须包含正负序电压，可采用正负电压分离控制或在正序控制外环中控制包含正负零序分量的交流总电压。

2）与采用定直流电压控制或定功率控制策略不同，电压前馈宜采用瞬时值前馈。

3）令交流电压外环和电流内环PI 控制器比例系数的乘积等于1。

4）在满足系统动态性能的前提下，应使电流内环PI 控制器的比例系数尽可能小。

5 阻抗扫描及中高频谐振特性分析

5.1 柔性直流换流器等效阻抗扫描

为了验证阻抗模型的正确性，在PSCAD/EMTDC 中对柔性直流换流器进行阻抗扫描，仿真模型结构如附录A 图A3 所示。阻抗扫描范围为10～5 000 Hz，其中10～2 500 Hz 范围内扫描频率间隔为50 Hz，2 500～5 000 Hz 范围内扫描频率间隔为100 Hz，仿真步长为10 μ s。本节主要针对以下2 种工况对换流器等效阻抗模型进行验证，得到阻抗扫描结果和理论计算结果如附录A 图A4所示。

工况1:正序控制中采用正序电压外环正序电流内环控制策略，负序控制中采用负序电流控制，无电压前馈低通滤波器。

工况2:满足阻抗改善措施的4 点要求，采用交流电压、电流正负序分离控制，无电压前馈低通滤波器，交流电压电流控制环PI 控制器比例系数乘积等于1。

由附录A 图A4 可见，当交流电压控制量仅为正序电压时，由于电压前馈和1/4 工频周期延时滤波器的作用，换流器阻抗在中高频段存在多处谐振峰和宽频负阻尼特性，并且伴随着200 Hz 左右的振荡。采用本文所提阻抗改善措施后，换流器阻抗中高频段和负阻尼特性得到有效抑制，换流器阻抗仅在500～1 500 Hz 范围内存在少量由电流内环控制与系统延时共同作用产生的负阻尼特性，该负阻尼特性可以通过减小电流内环PI 控制器比例系数进行抑制。另外，对比阻抗扫描和理论计算结果，二者基本一致，验证了V/f控制下柔性直流换流器等效阻抗模型和中高频阻抗重塑措施的有效性。

5.2 66 kV 交流汇集海上风电柔性直流送出系统中高频谐振特性分析

当海上风电柔性直流送出系统风电场采用66 kV 交流汇集方案时，由于取消了海上升压变压器，风电场侧阻抗感性特性降低、容性特性增强，系统发生中高频谐振风险提高。因此，本节以66 kV交流汇集的海上风电柔性直流送出系统为例，对中高频谐振特性进行分析。

在PSCAD/EMTDC 中搭建如附录A 图A5 所示的海上风电柔性直流送出系统，其中柔性直流换流器系统参数与附录A 表A1 相同。由于本文主要关注柔性直流换流器对系统中高频谐振特性的影响，海上风电场侧等效阻抗采用扫描的方式获取。柔性直流换流器采用交流电压正负序分离控制，采用瞬时值电压前馈，电流环PI 控制器比例系数为1，改变电压环PI 控制器比例系数，得到海上风电场与柔性直流换流器阻抗对比曲线如图5 所示。风电场等效阻抗存在一个高频固有谐振点，主要由海底电缆引起。

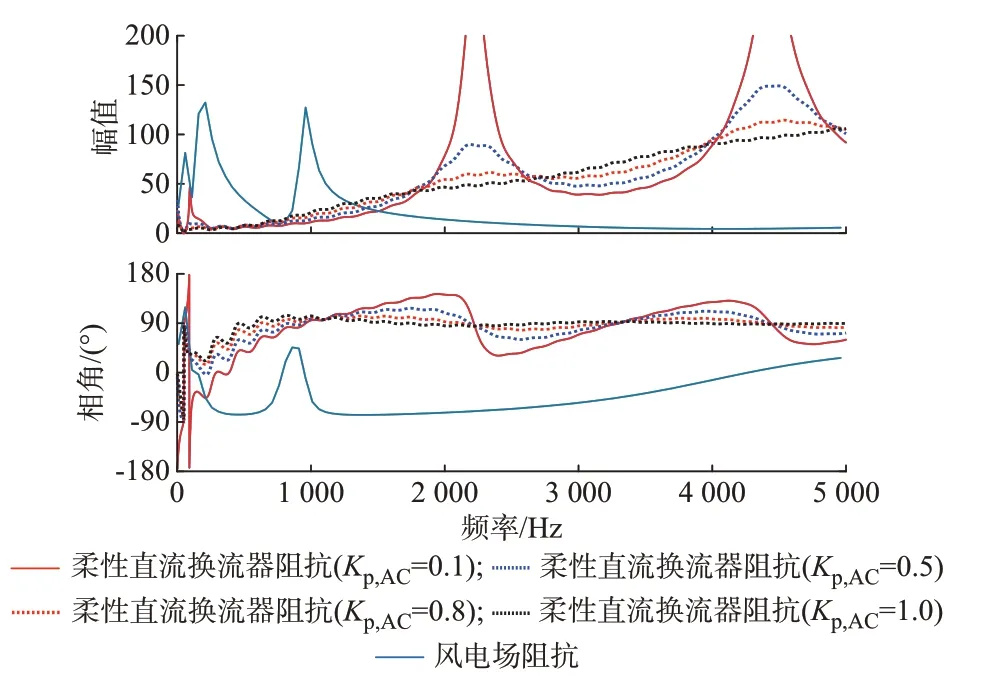
图5 海上风电场与柔性直流换流器阻抗Fig.5 Impedances of offshore wind farm and flexible DC converter

如图5 所示，当电压外环PI 控制器比例系数Kp，AC在0.1～1.0 范围内变化时，Kp，AC越小，柔性直流换流器阻抗特性曲线谐振峰幅值越大、负阻尼越严 重，主 要 原 因 为Kp，AC越 小，Kp，i和Kp，AC的 乘 积 越小，交流电压外环扰动项对电压前馈扰动项的抵消作用越弱。当Kp，AC为0.1 和0.5 时，柔 性 直流换流器与风电场阻抗幅值曲线分别在1 510 Hz 和1 410 Hz的交点处阻抗相角差大于180°，相角差分别为198.9°和187.2°，存在谐振风险。

在PSCAD/EMTDC 中对中高频谐振特性分析进行验证，得到并网点电压、电流波形如附录A图A6 所示，并网点电压频谱分析图如附录A 图A7所示。在0.2 s 前柔性直流换流器交流电压外环PI控制器比例系数Kp，AC为1，系统能够保持稳定运行；0.2 s 时Kp，AC切换为0.8，系统仍然保持稳定；0.3 s 时Kp，AC切 换 为0.5，系 统 发 生 频 率 约 为1 410 Hz 的 谐振，与理论分析结果基本一致。综上，验证了中高频谐振特性分析的正确性以及本文所提抑制措施的有效性。

6 结语

本文建立了V/f控制下柔性直流换流器的正负序等效阻抗模型，分析了其中高频谐振特性，并提出了一种中高频阻抗重塑措施，得到如下结论:

1）本文建立的V/f控制下的柔性直流换流器正负序阻抗模型计及了正负序交流电压外环、电流内环、电压前馈、系统调制和链路延时等因素的作用，适用于中高频谐振特性分析。

2）交流电压控制方式、电压前馈控制方式、电压外环和电流内环的PI 控制器比例系数大小、控制系统链路延时大小等因素均对柔性直流换流器的中高频阻抗特性有较大影响。

3）为改善换流器中高频阻抗特性:交流电压宜采用正负序分离控制（或在正序电压外环中控制交流总电压）；电压前馈宜采用瞬时值，通过优化交流电压外环和电流内环PI 控制器比例系数来抵消交流电压控制和电压前馈引入的扰动项；尽可能减小电流内环PI 控制器的比例系数和控制链路延时大小。

后续还将进一步研究V/f控制下柔性直流输电系统中高频谐振的抑制措施，在兼顾动态性能的前提下有效实现中高频谐振的抑制。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。