换流器并联运行的直流配电系统振荡分析
刘 磊,彭 克,王 琳,姚广增,李喜东
(山东理工大学,山东 淄博 255000)
0 引 言
直流配电技术与传统交流配电技术相比,具有供电容量高、线性损耗小、电能质量高等优点。此外,随着直流用电设备及分布式电源大量接入交流配电网,诸多的电力电子变换环节给交流配电网的安全可靠运行带来了影响。直流配电网能够更灵活地消纳直流负荷及分布式电源,必将会成为未来城市配电系统的重要组成部分。目前直流用电设备日益增多,为满足用电容量需求,采用换流器并联的直流配电拓扑结构,但直流配电系统固有的低惯性、弱阻尼特性易导致系统振荡,尤其采用并联换流器的拓扑时,需要进一步探究其振荡机理。
文献[3⁃5]研究了直流配电网振荡的原因,包括低阻尼LC环节与直流母线电压控制单元的交互作用、恒功率负荷的负阻抗效应、下垂系数的影响、多端互联的功率交互等;文献[6]首先建立多换流器并联系统的诺顿等效电路,定量分析谐振峰分布,求解谐振频率表达式,分析了系统参数对谐振的影响;文献[7]结合系统的阻抗模型和节点阻抗矩阵,提出基于阻抗的单母线谐振分析方法及系统级谐振分析方法分析谐振机理,并设计有源阻尼补偿器消除了谐振回路;文献[8]将两台逆变器与同类激励源合并为多逆变器并联系统小信号模型,分析谐振与逆变器控制和同步性之间的关系;文献[9]提出逆变器入网电流和滤波电容电流双闭环系统的输出阻抗建模方法,基于无环路阻抗耦合和引入数字控制延时逆变器输出阻抗模型,建立多逆变器并网系统的阻抗网络模型,分析谐振机理,发现逆变器产生谐波成分与电网电压谐波成分会加剧入网电流谐波畸变;文献[10]根据单台变流器诺顿等效电路定义其输出阻抗,基于阻抗法准确求解了多变流器并网系统的电网阻抗临界稳定值与失稳振荡频率。
目前直流电压振荡现象的研究中,电压源型换流器与恒功率负荷大多以级联的形式连接,所以普遍认为造成失稳的原因是恒功率负载的负阻抗特性,但在实际情况中,并联换流器间容易发生交互作用造成系统振荡,本文将着重从该点入手,得到VSC_1作为激励源的系统RLC并联回路,分析并联换流器系统的稳定性及振荡频率。
1 两换流器并联的直流配电系统稳定性模型
两换流器并联的直流配电系统的拓扑结构如图1所示,两换流器均通过⁃下垂控制的方式实现功率均衡控制。为分析换流器并联方式的振荡机理,下文将建立换流器、直流线路和直流负荷的动态导纳模型,三部分共同构成完整的配电系统。

图1 两换流器并联的直流配电系统拓扑图
1.1 下垂控制原理
直流配电系统是否稳定关键在于直流电压,因此本文选择⁃下垂控制,⁃指的是换流器输出有功功率和换流器直流侧电压之间的线性关系,利用该控制可以调节换流器的有功功率输出,并维持电压稳定。⁃下垂控制原理如图2所示。

图2 P⁃U dc下垂控制原理图
由下垂控制原理图得到换流器下垂表达式如下:

1.2 单个换流器的小扰动稳定性模型
单个换流器小扰动稳定性模型是指图1所示的电网母线与直流母线间整体部分的建模,即包括换流器、滤波器、交流线路、交流母线等部分。其中换流器采用下垂控制,控制框图如图3所示。

图3 换流器控制框图
⁃下垂控制运行在单位功率因数模式中,对直流侧有功功率作线性化小扰动,得到:
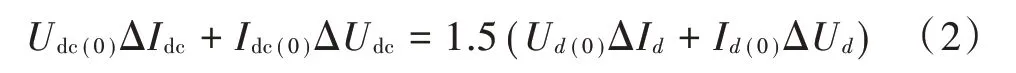
式中:Δ表示某一时刻的运行值与稳定运行值的偏差;下标(0)表示稳定运行值;U 为换流器输出交流电压在轴上的分量;I 是换流器输出交流电流在轴上的分量。
考虑交流线路阻抗参数及滤波器对小扰动的影响,得到:
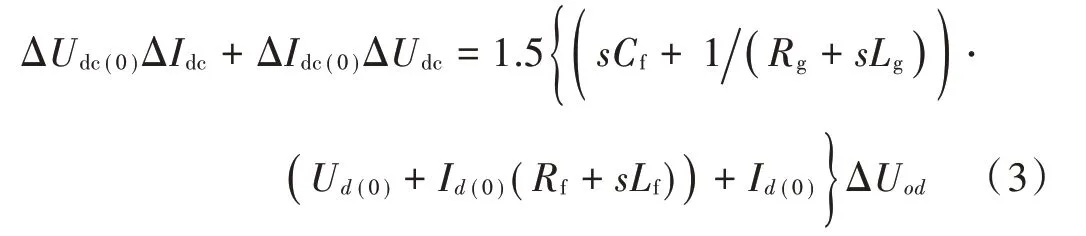
式中:,表示滤波器的电阻和电感,是与电抗器并联的接地电容,三者构成滤波器;和是与电网母线直接相连的交流线路的电阻和电感;U 是与电网母线直接相连的交流母线的电压。
对电压外环控制器在轴上产生的电流信号参考值I 及换流器产生的轴调制解调信号P 作小扰动,并联立式(2)和式(3),可得单个换流器交流侧的输入导纳,即小扰动稳定性模型表达式Δ如式(4)所示:
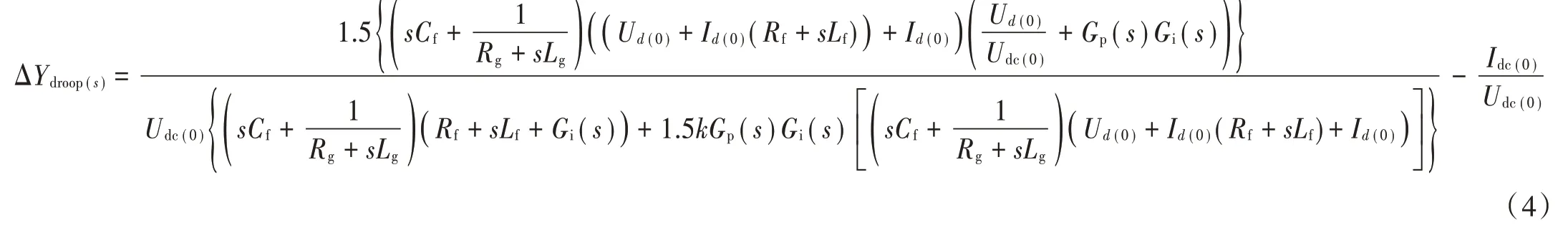
1.3 多换流器并联的小扰动稳定性模型
以两并联为例分析,其含义是两个换流器小扰动稳定性模型交流侧共同并接于电网母线,直流侧共同并接于直流母线,即换流器的并联是交流侧与直流侧都并联,换流器VSC_1和VSC_2均采用⁃下垂控制,因此,并联两换流器的小扰动稳定性模型表达式与式(4)相同,分别用Δ,Δ表示,根据电路原理,并联电路总导纳等于各个支路的导纳之和,所以两并联换流器的小扰动稳定性模型为:
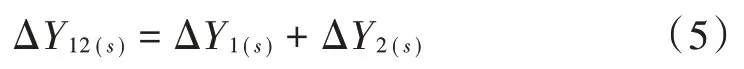
基于以上论述可知,根据单个换流器小扰动稳定性模型快速求解多换流器并联时小扰动稳定性模型,当个换流器并联运行时,各个换流器小扰动稳定性模型为式(4),分别用Δ,Δ,…,ΔY 表示,则多换流器并联的小扰动稳定性模型见式(6),该式表征了电网母线与直流母线间所有的换流器模型。

1.4 直流负荷及直流线路稳定模型
1)直流负荷稳定性模型
本文假定直流负荷功率恒定,直流负荷处的电流为:

式中是负荷有功功率。对式(7)做线性化小扰动,可以得到直流负荷的输出导纳为:
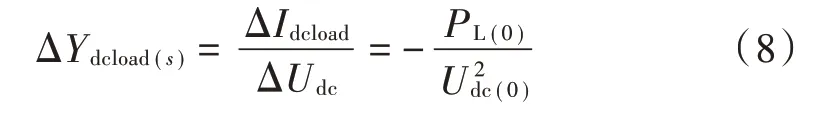
直流负荷的导纳为负值,表明其具有负阻抗特性,易导致系统不稳定,导纳幅值由负荷有功功率和直流母线电压两者决定。
2)直流线路稳定性模型
在本文中,采用π型集中参数等值电路模型代替直流线路,直流线路导纳Δ为:
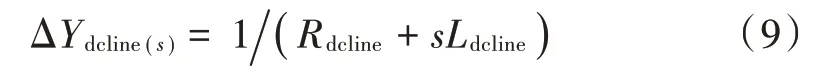
因此,考虑负荷时的直流侧输出导纳,也即直流侧稳定性模型,表达式为:

以图1中的直流母线为源荷分界点,多换流器并联的交直流互联配电系统的传递函数为直流侧负荷及线路的输出导纳与换流器交流侧输入导纳之比,式(11)为交直流配电系统稳定性分析的基础。
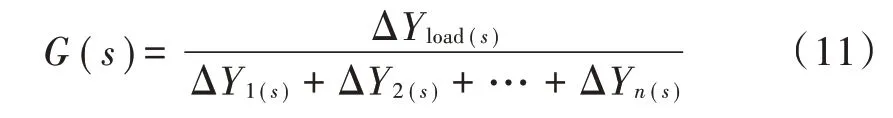
2 谐振分析方法
2.1 基于频域法的谐振机理分析
随着并联换流器数目的增多,各换流器易表现出不同的导纳特性,换流器与电网导纳间,多个换流器的内环控制器之间、外环控制器之间、甚至是内环电流控制与外环电压控制之间均有可能发生交互耦合作用,引发不稳定现象,导致系统阻尼减小,稳定裕度降低。以图1两换流器并联系统为例,考虑直流负荷、直流线路影响的等效电路如图4所示。换流器和换流器交流侧电抗器等效为电流源,交流线路阻抗、滤波电容等效为交流侧无源网络,直流负荷、直流线路阻抗+j等效为直流侧输出无源网络。不计直流线路电压损耗,且负荷有功功率为20 kW,求得直流有功负荷为8Ω,呈阻性。

图4 两换流器并联系统的简化模型

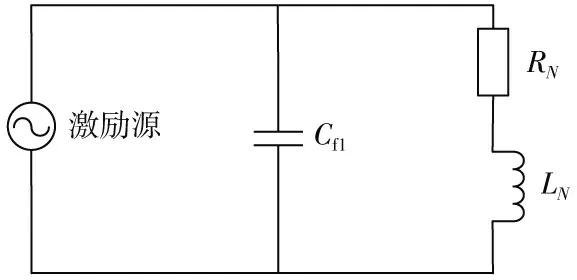
图5 VSC_1作激励源的振荡电路简化模型
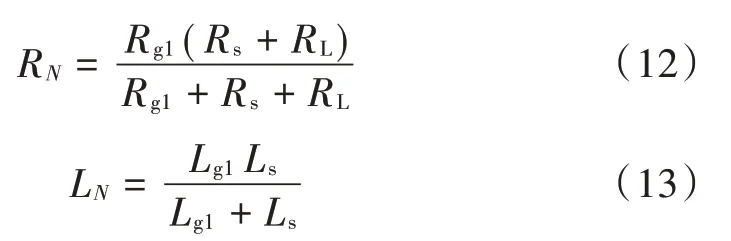
式中:R 为交直流线路电阻,+并联后的总电阻;L 为交直流线路电感,并联后的总电感。
首先推导出并联RLC电路总导纳的标准形式:

由电路原理可知,令式(14)虚部为零,即得到振荡频率表达式为:

将式(12)和式(13)代入,得到两换流器并联系统直流母线电压振荡频率表达式为:
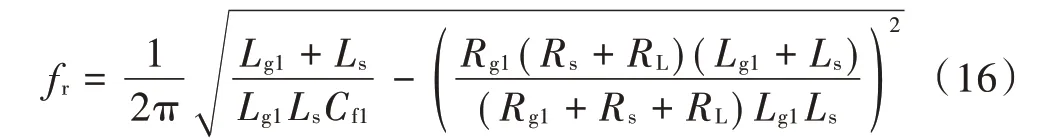
根据式(16),滤波器输出电流受控于给定的电流指令值,因此其电感、电阻值并不改变电路的振荡频率,对系统振荡频率起主要作用的是直流线路、直流负荷、交流线路以及并联电容器参数。另外,换流器的并联数目也不影响振荡频率,主要改变振荡的幅值。
为验证上述论据的正确性,首先根据式(11)在Matlab中表示出单一换流器系统以及两换流器并联系统的传递函数,利用奈奎斯特曲线比较两种模式下系统的稳定性情况,如图6所示,单换流器模式下,直流母线电压未发生失稳;而两换流器并联模式下,奈奎斯特曲线与轴的交点位于(-1,j0)的左侧,理论上会出现失稳现象,具体参数如表1所示。
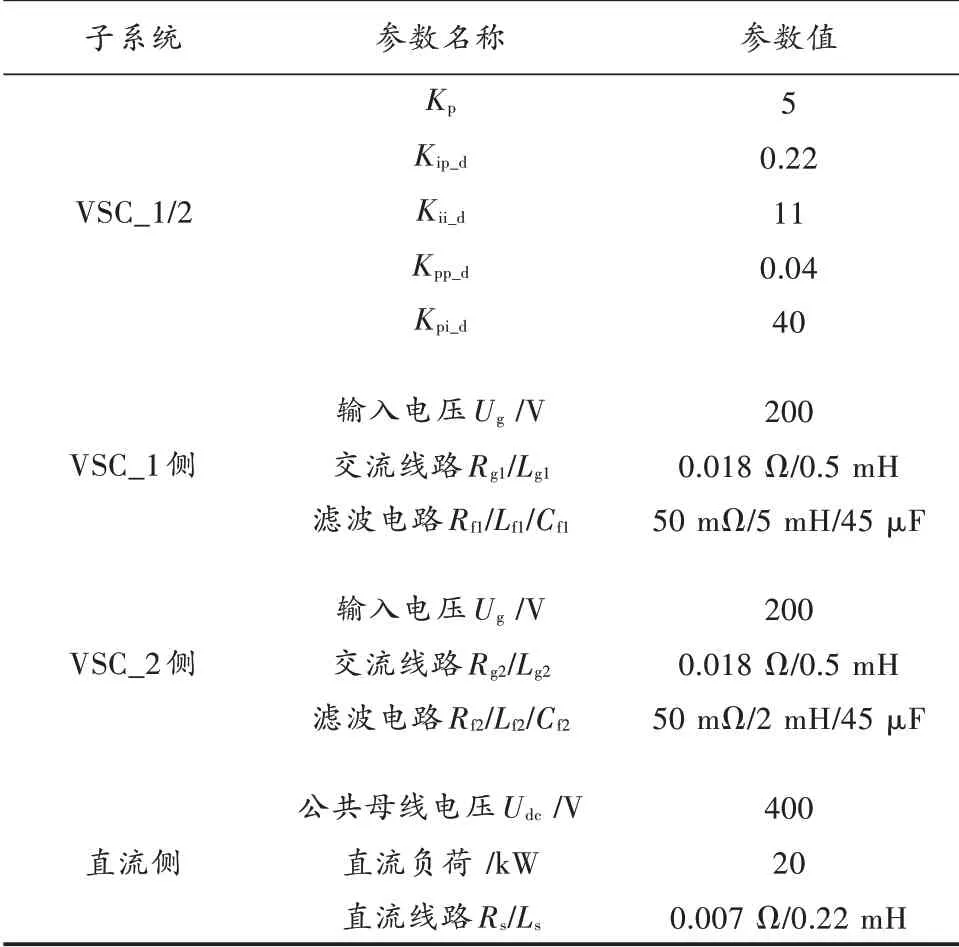
表1 直流配电网系统参数

图6 直流配电系统的奈奎斯特图
通过波特图可以进一步分析并联失稳时的频率响应,如图7所示,系统在低频段出现谐振峰值,峰值处对应的频率为8.1 Hz,即为系统的振荡频率。经计算,该值与式(16)求得的近似相等,说明机理分析是正确的。换流器动态导纳将在处达到最大值,不满足并网换流器性能优良的必要条件,即换流器输入导纳幅值在各个频率段越小越好。由波特图可知,系统幅值裕度为-2.17 dB,对应的穿越频率ω为0.798 Hz,谐振峰值处的幅值大于0 dB,相位小于-180°,因此可以确定直流母线电压是不稳定的,会出现低频振荡。

图7 直流配电系统的波特图
2.2 时域仿真验证
在DIgSILENT仿真软件中搭建如图1所示的交直流配电系统仿真算例,参数仍按表1设置。仿真时间设置为5 s,直流母线电压的仿真波形如图8a)所示,电压表现为正弦式的振荡,随着时间的增加,振荡幅值逐渐增大,3.47 s后变为等幅的正弦振荡,等幅振荡频率为7.69 Hz,与2.1节理论分析所得的结果基本一致。另外,单一换流器配电系统的直流母线电压未出现失稳,仿真曲线如图8b)所示。

图8 单一以及两换流器并联系统直流母线电压仿真波形
3 直流电压振荡的主要影响因素
3.1 下垂系数对振荡的影响
以两并联换流器系统为例,当下垂系数增大时,根据换流器导纳式(4),输入导纳Δ的值减小,输入阻抗幅值增大,有利于提高稳定裕度;此外,下垂系数存在于换流器的外环控制中,其值的增加减弱了两换流器的外环控制器间的动态交互作用,这也意味着交互强弱与下垂系数的大小呈负相关。采用表1中的参数,逐渐增大VSC_1和VSC_2的下垂系数及,其余参数均保持不变,下垂系数变化时的奈奎斯特曲线如图9所示。当==5及==6时,奈奎斯特轨迹包围了(-1,j0)点,直流母线电压失稳振荡,而==7时,奈奎斯特轨迹未包围(-1,j0)点,即奈奎斯特曲线与轴的交点位于(-1,j0)点的右侧,系统稳定。随着的增加,系统的稳定性逐渐变好,逐渐由不稳定向稳定过渡,但=7时,奈奎斯特曲线与轴的交点距离(-1,j0)点较近,故系统的稳定性较差,且换流器下垂系数不宜过大,因此,仅通过调节下垂系数不足以使系统获得较好的稳定性能。

图9 下垂系数K p不同时的奈奎斯特图
不同下垂系数的直流母线电压时域仿真波形如图10所示,下垂系数对母线电压的振荡频率影响较小,随着的增大,振荡频率略微升高,=5及=6时,直流母线电压的振荡频率分别为7.69 Hz和8.33 Hz。
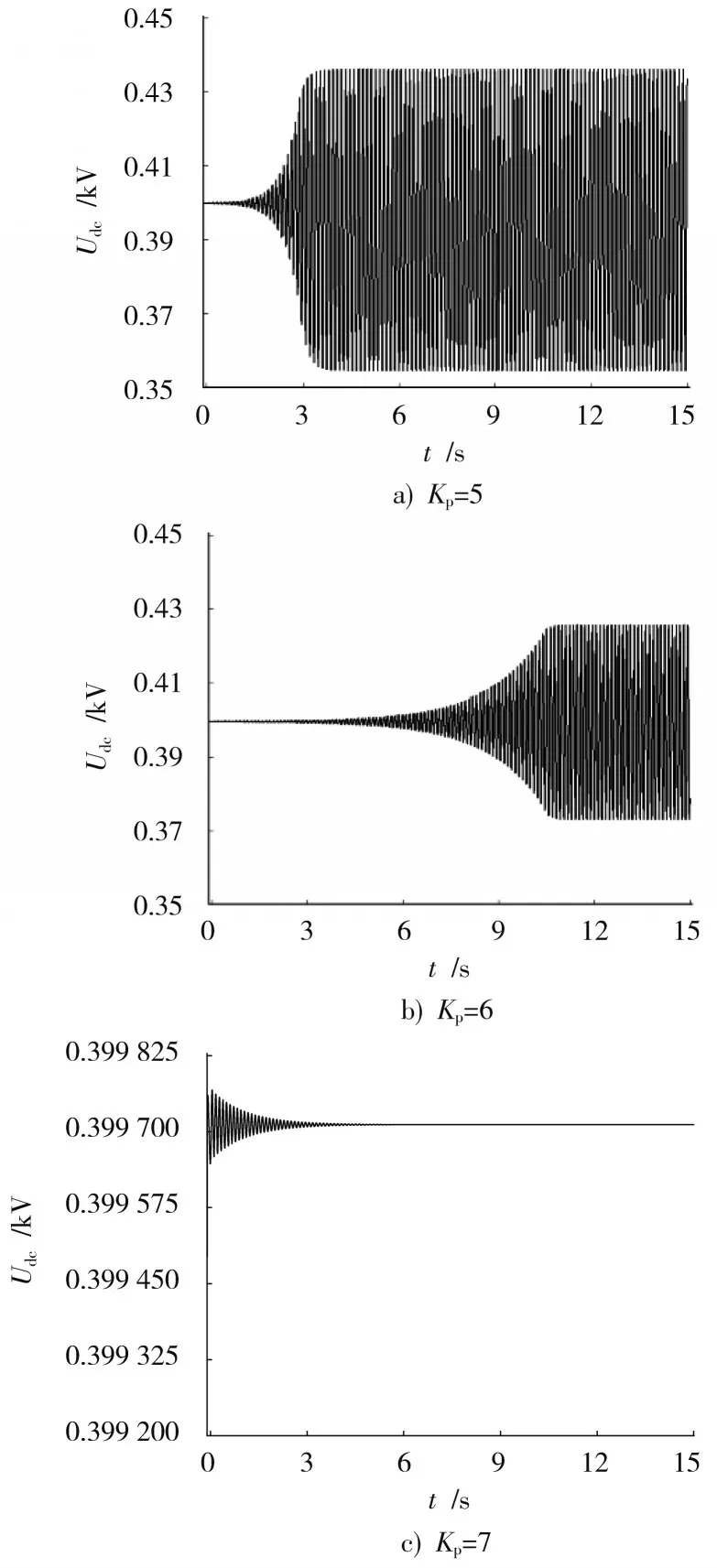
图10 K p不同时的直流母线电压仿真波形
3.2 交流线路电感L g对振荡的影响
交流线路电网电感相对换流器滤波电感来说非常小,极易被忽视。在配电系统中,当传输线路长度超过一定值时,交流线路参数需要考虑。
随着增大,换流器动态导纳小扰动幅度增大,两换流器回路间产生越来越多的低频谐波,其含量超过允许上限后,谐波激励源将会迅速接近振荡频率,换流器间的交互愈加剧烈,使换流器直流侧电压出现振荡现象。此外,增大后产生的低频谐波激励,增强了两换流器内环控制器间的交互作用,使并网谐波电流严重放大,降低了换流器电流控制的有效性,系统稳定性变差。在振荡频率时,换流器自身的导纳较大,网侧导纳相对较小,因此谐波电流只在两换流器间流动,而不会经过电网,导致系统的谐振为低频段的振荡,并且也说明了振荡是由于换流器间的相互作用产生的,与电网侧无关。两并联换流器系统中,同时改变表1中和的值,其余参数不变,由图11的奈奎斯特曲线可知,系统稳定性随着的增加变得更差。

图11 交流线路电感L g不同时的奈奎斯特图
变化时的时域仿真曲线见图12,的增加使得直流母线振荡频率略微变化,可以忽略不计,但振荡的幅值却明显增大,总体来说,系统的稳定性变差,电压遭到更严重的破坏,与频域分析结果一致。

图12 L g不同时的直流母线电压仿真波形
4 结 语
本文针对换流器并联运行的直流配电系统的振荡现象进行了研究,将两换流器交互失稳的机理分析简化为RLC并联回路振荡频率的求解,并采用频域分析与时域仿真相结合的方法验证机理分析的正确性,主要结论如下:
1)与单换流器模式相比,并联换流器模式不利于直流配电系统的稳定性。并联换流器结构下,滤波电感增大到临界值后,换流器输出电流将作为激励构成振荡电路,导致换流器间发生并联耦合使直流侧母线电压振荡,更严重的导致系统崩溃。
2)参数变化会对换流器稳定性模型的小扰动幅值产生影响,当两换流器的下垂系数同时增大时,换流器小扰动幅值减小,有利于实现系统的电流均分以及直流母线电压稳定;然而,当交流线路电感同时增大时,换流器小扰动幅值也随之增大,加强了两换流器间的耦合,不利于直流电压稳定。

