移动边缘计算中支持能量收集的计算卸载策略
蒋欣秀,杨俊东,杨志军,李 波,丁洪伟
(云南大学,云南 昆明 650500)
0 引 言
随着互联网的兴起,网络技术和应用服务的发展使网络流量呈现爆炸式增长,面对来势凶猛的流量增长,业界提出了移动边缘计算(Mobile Edge Computing,MEC)的概念。移动计算在一定程度上解决了用户终端计算能力不足的问题,但是对于具有时延敏感、计算密集、能耗巨大的新兴应用不断涌现,MEC服务器的局限性也日益凸显,因此,如何在边缘计算系统中设计合理的计算卸载策略满足用户需求具有现实的意义。
计算卸载在边缘计算网络中作为一种节约设备能源的有效手段和减少时延的重要方法,国内外很多学者对其做了大量研究,对于计算卸载的模式主要有三种方式:二进制卸载、部分卸载、随机卸载。文献[5]采用二进制卸载有效解决了任务时延和能耗均衡的问题,但任务的决策取决于终端设备的运行状态,系统的性能对设备的要求较高。任务卸载对于计算卸载的场景目前有单用户单个MEC服务器、多用户单个MEC服务器以及最复杂的多用户多个MEC服务器。文献[8]研究了多个任务之间卸载的顺序,提出一种优化算法均衡时延和能耗,但需要消耗大量的内存。文献[9]中利用整数规划的优化算法将部分卸载的计算任务建模为图模型,但对于接入的用户数增多,模型的复杂度也会随之增加。上述工作虽在一定程度均衡了时延和能耗,但处理器的能耗随其频率呈线性增长,导致其能耗过大。
基于上述分析,本文以多用户多MEC服务器为场景,建立了一种基于能量收集技术获取能源的移动边缘计算系统模型,采用动态电压频率调节(Dynamic Voltage and Frequency Scaling,DVFS)技术调节移动设备和MEC服务器的CPU最佳频率,使本地执行能耗和MEC服务器执行能耗降至最低。对于卸载策略存在时域耦合的问题,采用Lyapunov理论将问题转化为逐时隙定性问题求解,并将问题分解为能量收集和最优决策两个子问题,对于求解最优决策问题提出了一种改进的灰狼算法对CPU最佳频率和发射功率进行迭代以获取最小的任务执行代价。
1 系统模型
1.1 多用户多MEC服务器模型
首先,对多用户多MEC服务器模型做如下假设:
1)本模型由个移动用户和个MEC服务器组成,其中∈{1,2,…,,…,},∈{1,2,…,,…,}。MEC系统模型如图1所示;

图1 MEC系统模型
2)移动用户配备了能量收集组件收集可再生能源,供用户端计算和卸载使用;
3)模型为一个离散时间模型,τ表示一个时隙的长度;
4)每个服务器的位置是固定的,每个移动设备在相同的时隙内位置不变,在不同时隙之间随机变化;
5)信道独立同分布(Independently Identically Distribution,IID),用户通过无线信道访问服务器,在时隙信道增益为h ,信道增益在同时隙内保持不变,在不同时隙之间随机变化。
1.2 系统模型
定义指标变量ζ用以描述移动用户的任务请求,当用户在第个时隙内有请求时,ζ=1,否则,ζ=0,U (D ,B ,)表示用户在第个时隙产生计算密度为D 的任务,B 为卸载至MEC服务器的数据量,计算任务执行时间不能超过单个时隙的长度。每个被请求的计算任务可以在移动设备上执行,并将任务在本地成功执行表示为;电池电量不足时任务会被丢弃,把本地丢弃的任务表示为;任务也可以卸载到MEC服务器上执行,并将成功执行的任务表示为;由于受到信道深衰落的影响会造成任务丢弃,把传输丢弃的任务表示为;计算模式选择应满足以下约束:
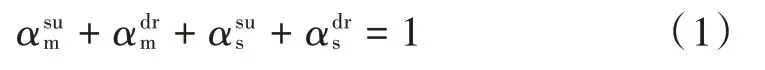
若在时隙用户有任务U (D ,B ,)请求在本地执行任务,将用户的CPU周期频率表示为 (),因此,第时隙用户在本地执行的时延表示为:
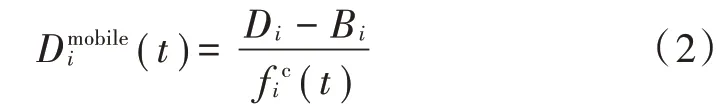
本地执行任务时用户所消耗的能量为:

式中: ≜( ())表示本地计算的消耗功率,为有效开关系数,为常系数,一般为2,执行频率受到CPU周期频率上限的约束,即 ()≤。
为计算卸载到MEC上的任务,本模型假设MEC服务器计算资源充足,且计算输出很小,因此不考虑回传的传输时延。将衰落信道功率增益表示为γ(),服从均值为1的指数分布,信道功率增益表示为h ()=γ()(d ()),其中为传递损失指数,表示路径损耗常数,d 表示第时隙用户与MEC服务器之间的距离。假设每个用户都有相同的带宽和噪声功率,根据香农公式,在时隙传输率表示为:

式中:是系统带宽;表示噪声功率;P ()表示用户的发射功率。如果任务由MEC服务器执行,传输时延表示为:

在第时隙中任务卸载至MEC服务器消耗的能量表示为:

在第时隙MEC服务器需要处理上传数据量为B 的任务,表示计算每bit数据所需的周期数,因此,第时隙MEC处理卸载任务的计算时延表示为:
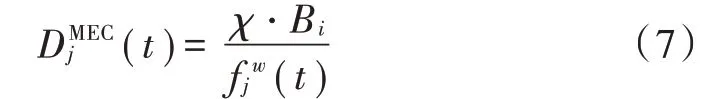
受到周围环境状态的影响,为了模拟能量收集过程中的间接性,把每个时隙到达移动用户的能量表示为e (),且满足0≤e ()≤,收集的能量存储到电池中用于下一个时隙的本地执行或卸载。在时隙开始时移动用户能量水平表示为C (),第时隙用户消耗的能量表示为ϑ(),考虑到移动用户维护基本运行需要一定的功耗,将其表示为,当有任务请求计算ζ()=1时消耗的能量表示为:

式(8)服从能量因果约束ϑ()≤C ()<+。
根据式(8),用户的电池能量级按照式(9)进行迭代:

1.3 执行代价模型
由于能量收集存在随机性和中断性,当本地缺乏能量时会造成一些任务被丢弃,本模型对丢弃的任务给予执行代价惩罚。因此执行代价表示本地计算时延、任务上传时延和服务器计算时延三个部分,定义为:

式中:为任务丢弃的惩罚权重;()为指标函数。因此,对于本模型的平均执行成本最小化问题可以表示为:

约束条件说明:S表示在同一个时隙中每个用户只能选择1或0两种模式;S表示每个用户在同一个时隙中有且只有一种模式;S为电池电量的上限约束;S表示本模型在每个时隙时消耗的能量不超过开始时隙的电量;S表示用户和MEC服务器CPU周期频率的上限;S表示用户发射功率不超过最大发射功率。
2 任务卸载决策
2.1 Lyapunov优化算法
Lyapunov优化算法是一种通过控制系统稳定性来解决多目标优化的问题,多用于独立同分布模型。由于系统的决策、电池能量水平均与时间相关,不能直接使用Lyapunov优化技术,因此,提出了加权扰动方法将与时间相关的问题转化为逐时隙确定性问题,移动用户的扰动参数定义为、虚拟能量队列φ(),并将两者的关系定义为:

式中 :扰动参数满足≥+⋅,=min{max{(),τ},}表示在第个时隙用户实际消耗能量的上限。在时隙将不同的用户频率和服务器频率标准化为 ()=f (),f ()=f (),针对虚拟队列表达式(12)将二次型Lyapunov函数定义为:

式(13)通过对更新队列求平方和,表示在时隙各队列中电池能量的多少,该函数值越大说明电池中能量越多,在时隙τ下的单步Lyapunov漂移函数表示为:

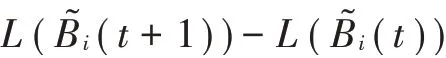

式中=2(+)。本模型的Lyapunov漂移加罚函数定义为单时隙Lyapunov偏移与执行成本的加权差为:

式中是控制系数,用于权衡代价函数和虚拟队列的稳定性。
根据Lyapunov漂移加罚函数的上限值可将最优的执行代价模型表示为:
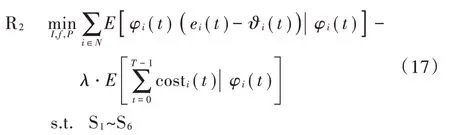
2.2 能量收集和最优卸载决策
R是一种由Lyapunov理论优化的优化格式,根据文献[15],R问题可分解为能量收集和卸载决策两个子问题。
本模型假设每个移动设备都配备一个EH模块且每个用户在每个时隙收集的能量是独立的,每一个EH模块的充放电过程可以同时进行。设定一个充电阈值M =0,当设备的能量低于阈值时,电池与负载断开以保护系统,在第时隙内可收集的能量表示为Q (),成功收集的能量为q (),EH成功收集到的能量约束为q ()∈[ 0,Q ()],由于电池容量有限,成功收集的能量q ()受最大电池容量约束q ()≤,由于配备EH模块的模型执行卸载策略较为复杂,本模型理想化考虑通过获得各个用户的所有时隙中最优的e (),即可得出最优的能量收集。根据式(17)可将用户收集能量的问题表示为:

在与目标函数式(17)解耦之后,可以将过时隙的问题简化为:

当ζ()=1时,R包括了本地执行、卸载执行、任务丢弃三个部分,根据式(8)、式(10),通过求解R的最小值以获得最优卸载决策M (),其数学模型表示为:

式中:m (f )表示本地执行代价函数的最小值;m (f ,P )表示卸载执行代价的最小值。通过比较m (f ),m (f ,P ),m 的大小,选取其最小值为最优卸载决策,当任务被丢弃时有m =+φ,如果任务选择在本地执行,根据式(8)、式(10)、式(17)可将本地执行代价模型表示为:

如果任务卸载至边缘服务器执行时,根据式(8)、式(10)、式(17)把卸载执行代价模型表示为:

2.3 基于改进灰狼算法的模式决策
为了求解本地执行代价和卸载执行代价模型的最小值,获得最优卸载决策,根据式(21)和式(22)需对CPU频率和发射功率在多约束条件下进行寻优,因此,引入一种灰狼算法对模型进行迭代,通过获取最佳CPU频率和发射功率,实现最优模式的选择。
灰狼优化(Grey Wolf Optimization,GWO)算法是一种仿生群智能算法,模拟了狼群的等级制度和捕猎行为,种群按照其严格的等级制度进行寻优,每一头狼个体代表一个优化值,最优解为狼,次优解为狼,第三优解为狼,优化过程可建模为:
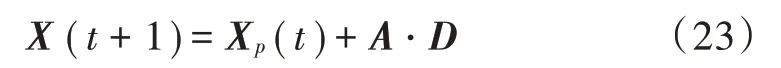
式中:X 表示猎物的位置;表示灰狼的位置;=|⋅X ()-()|表示灰狼和猎物之间的距离,其中2⋅,,为系数向量,且有=2⋅-,=2-⋅2,,为[0,1]之间的随机矢量,是平衡全局搜索和局部搜索的参数,在每次迭代中保留最优的三个解,利用这三个解进行最优位置的更新,可表示为:

式(24)表示,,与其他狼之间的距离,式(25)表示狼在,,狼的引导下进行位置更新,由式(26)可得出全局最优的位置。
在基本GWO中,参数对灰狼群体的寻优过程有重要影响,利用GWO迭代计算最优频率和最优发射功率时,控制参数线性递减策略很难适用于该寻优过程。针对这一问题,本模型基于指数规律变化的非线性收敛因子,提出一种改进的灰狼PGWO(Parameter Grey Wolf Optimization)算法,其数学模型为:
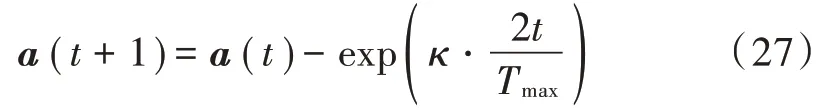
式中:为当前迭代次数;为最大迭代次数;为调节参数。在卸载中灰狼每一个个体代表一个频率值,猎物代表全局最小值,为了求解m (f )和m (P )的最小值以获得最优卸载决策,可将求解流程表示为图2。

图2 基于PGWO的模式选择流程图
3 仿真实验分析
3.1 仿真实验环境
为了验证本模型的有效性和优越性,使用Matlab R2018b软件进行仿真,计算机仿真操作环境为:IntelCore™i7⁃7700 CPU@3.6 GHz,仿真参数如表1所示。

表1 参数说明
本模型考虑5个MEC服务器和5个用户,用户在距离每个服务器半径50 m的范围内随机分布,仿真执行400个时隙,每个时隙的长度设为2 ms。
3.2 实验结果与分析
在不同种群数量下对改进的灰狼算法进行验证,结果如图3所示,在不同的计算规模下,改进的灰狼算法运行时长明显低于其余两种算法。为了验证该改进算法适用于本模型,对三种算法在适用函数相同的情况下进行了对比,结果如图4所示。

图3 用户数与时间关系
由图4可知,改进的灰狼算法和灰狼算法趋势相似,但改进的灰狼算法在迭代300次时开始趋于收敛,且执行代价较小,可用于本模型的分析。

图4 迭代次数和执行成本关系
由于自然界中的可再生资源(风能、太阳能)存在不连续的问题,移动用户用于卸载任务和本地计算任务的能量需要连续性,以保证用户体验质量。因此基于上述问题,对本算法的移动用户电池能级进行了测试,结果如图5所示。随着时隙的推移,各个移动用户电池能级在前期不断进行积累,最终稳定在扰动能级附近,在当前的参数下,各个移动用户的电池能级在第200时隙开始稳定,稳定后的电池电量将完全用于下一个时隙的任务卸载和本地任务计算,有效地验证了能量收集的可行性。

图5 各用户能量收集与时间关系
计算模式的选择决定了系统代价的大小并影响了用户体验质量。在本模型中,当电池能级不足以支持任务的计算,任务将被丢弃,用户体验质量会随着丢弃的任务增多而变低,同时用户体验质量与执行时延有关,执行时延基于对卸载代价、本地计算代价的比较选择代价较小的模式。
图6比较了多用户多MEC服务器各模式选择的比例,在开始阶段,由于能量级别较低,大量的任务被丢弃,随着电池能级趋于稳定,任务丢弃率下降至0,在前100个时隙中,平均丢弃率为2.7%,平均卸载率达到90.6%,表明卸载到MEC服务器上的执行代价是最小的。

图6 任务执行的模式选择比例
执行代价是任务处理的时延和能耗任务丢弃率的评价指标,从图7中可以看出,每个移动用户在开始时隙执行代价很高,这表明开始时隙电量能级较低,时延和能耗以及被丢弃的任务会增加,随着时隙的推移,执行代价趋于一个稳定的区间[0.05,0.09],可说明本算法经过迭代寻找到执行代价最优值。

图7 各用户平均执行成本与时间关系
图8描述了不同算法下的执行代价随时隙变化的情况,其中三种算法都随着时隙的推移趋于一个稳定的值,都能寻找到执行代价最优的值,然而改进的灰狼算法比灰狼算法和遗传算法收敛更快,因此,在时间收益上优于其余两种算法。

图8 不同算法平均执行成本与时间关系
根据图9可以看出,在MEC服务器数目不变的情况下,用户数量的增多会导致执行代价的增长,但是遗传算法和灰狼算法在用户数量增加时的执行代价均大于改进的灰狼算法,因此,本模型的算法具有较好的性能。

图9 三种算法执行成本与用户数量的关系
4 结 语
本文研究了在多用户多MEC服务器场景下,支持用户收集能量的边缘计算卸载问题,意在通过选择合适的负载均衡模式和最大化能量收集策略,改善移动边缘计算表现,以提升系统用户体验质量。本模型基于能量收集技术,将收集的能量用于任务的执行,节省了大部分的能源,以任务执行代价为目标,将最优卸载策略抽象为时延、能耗和丢弃惩罚均衡问题,利用Lyapunov理论解决了时域耦合问题且将问题分解为能量收集和最优决策问题,并基于改进的灰狼算法对最优决策问题进行求解。实验证明,本文提出的可支持能量收集的边缘计算卸载策略对于多用户多MEC服务器的场景具有很好的鲁棒性。

