基于距离矢量的多传感器信息决策算法

张凌飞，马 俊，陈博行

（1.青海师范大学 计算机学院，青海 西宁 810008；2.青海民族大学 物理与电子信息工程学院，青海 西宁 810007）

0 引 言

随着5G时代的到来，加速促进“万物互联”进程，传感器网络作为机器感知世界的重要媒介，其安全性、智能性、先进性直接影响着社会的发展与进步。一个完整的传感器网络通常由多个传感器节点组成，这些传感器节点看似独立，实际由于监测范围、方式和对象等的关联性，各数据之间有潜在的内在联系，信息决策正是利用这种内在联系，通过算法自动决策出相对正确的结果，为科学研究做出参考。

文献[6]针对冲突证据决策存在的问题，提出了一种基于二次组合的证据决策方法，通过仿真分析，该方法能够较好地解决证据冲突问题，且计算量减少了5~10 dB；文献[7]提出了一种基于混合权重距离的毕达哥拉斯模糊TOPSIS的多属性决策方法，该方法可通过调节提高算法的应用范围；文献[8]针对属性权重完全未知的混合型多属性决策问题，提出了基于前景理论和证据理论的混合型多属性决策方法，经过分析该方法有较强的区分能力；文献[9]使用SVDD方法改进D⁃S证据理论，并建立两级融合模型进行验证，实现多等级、多层次的诊断，结果表明该诊断方法正确率高达93%；文献[10]提出了一种基于证据理论和群体决策的综合信息融合方法，根据焦点元素一致性函数调整合取和析取规则的权重，经仿真对比，该方法可以获得合理可靠的决策结果；文献[11]针对D⁃S证据理论的冲突问题，提出了一种基于置信度的证据理论的改进策略，算法采用4个神经网络的初步预测值提取权重，合理构造了BPAs函数，并通过实例验证了该系统的应用效果；文献[12]针对D⁃S证据理论存在的高冲突，通过对相似性Jaccard系数矩阵分块化处理，计算各传感器节点的权值修正证据源，以降低D⁃S证据理论决策风险；文献[13]针对CPSs提出了基于模糊集和D⁃S证据理论的数据融合算法，该算法首先采用模糊集理论和属性权重确定证据的分布，并将属性证据的数据融合与CPSs中传感器节点的可信度相结合。以上决策方法计算过程较为复杂，大多在算法中需对传感器采集数据进行概率赋值，且较少考虑传感器自身特点和评价标准。本文充分利用监测系统中传感器数据评价等级范围，结合实际测量值，利用实际值与标准值之间的距离计算各传感器数据间的支持度，最终得出系统决策结果。

1 多传感器信息决策模型

图1为多传感器信息决策模型。由图1可知，决策过程中充分利用了系统评价标准，根据已知评价标准与各传感器节点采集数据对应的实际值做比较，得出相应的距离差，再将各评价标准对应的距离差求和，得到后者对前者的支持度，通过数据处理算法得出各组决策结果的优势度，取优势度最大作为决策的输出结果。

图1 多传感器信息决策模型

2 算法原理

2.1 单属性信息融合算法

图2为一维传感器信息决策原理图。假设在某监测系统中使用同类传感器进行测量，系统预设有4个评价等级，评价等级一的取值范围为±Δ，其余3个评价等级的取值范围如图2所示。设为传感器实际测量值，计算到各取值范围中心值的距离的绝对值，取最小绝对值所在的评价等级范围作为最终决策结果。图2的决策结果为“决策结果二”。

图2 单属性信息决策原理图

2.2 多属性信息融合算法

多属性信息决策原理如图3所示。其中，，…，为“决策结果一”对应的各传感器取值范围的中心值，同样，，，…，为“决策结果二”对应的各传感器取值范围的中心值，，，…，为第一组实际测量值。将单属性决策方法横向扩展到多属性信息决策，纵向计算实际测量值与标准决策范围中心值的距离矢量的模，横向计算各决策结果对应距离矢量模之和，该值越小，表明计算结果越接近该决策结果。

图3 多属性信息决策原理图

3 基于距离矢量的多传感器决策算法

定义1：在某评价系统中共有个评价等级，传感器共个，每个等级对应的第个传感器的取值范围为a ±Δt ，其中心值为a ，则等级可用向量G =(a ,a ,…,a )表示。

定义2：设每个传感器测量的最大值为max(a )，最小值为min(a )，实际测量值为向量=(,,…,b )，且min(a )≤b ≤max(a )。

定义3：设N 为评价对各个传感器测量值的支持度，φ=(A ,A )=b -a ，表示测量值b 到评价a 的距离，其中，≤，≤。

则得支持度矩阵为：

由式（1）得支持度函数：

定义4：归一化处理。

优势度函数结果为：

定义5：根据定义1~定义4的计算方案，得规范化函数为：

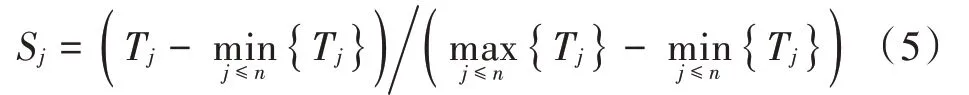
对S 计算结果进行排序，取max{S }为最优解方案，即此时S =1。

定义6：设为区分度函数，则：

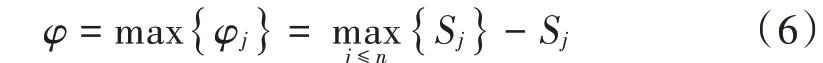
4 仿真算例

例1：假设现要对某一水域的温度进行分级，评价标准如表1所示。采用温度传感器对其进行测试，设测得当前水域温度为15℃。

表1 温度评价标准 ℃

由表1可得表2规范化函数计算结果。

表2 规范化函数计算结果

对S 计算结果进行排序，取max{S }为最优解方案，即该水域为三级。由式（6）得区分度为0.571 4。

例2：假设现要对某一水域污染情况进行综合评价，评价标准如表3所示。传感器节点采集水质环境参数（温度、p H、浑浊度、电导率），实际测量结果分别为：12℃，7.5，20%，0.4。

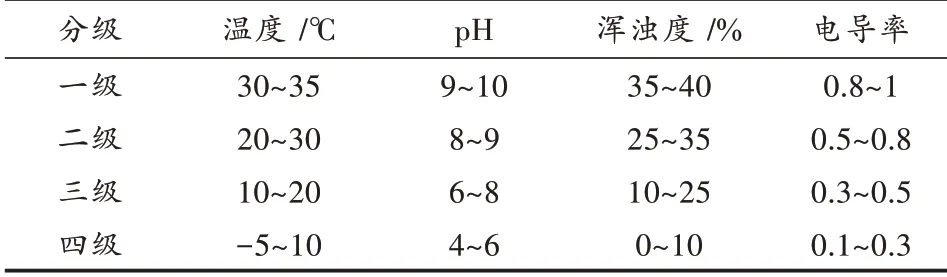
表3 水域污染评价标准

由表3得：

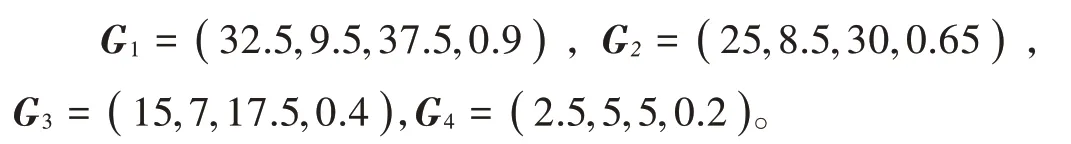
得支持度矩阵为：

由式（2）~式（4）得：

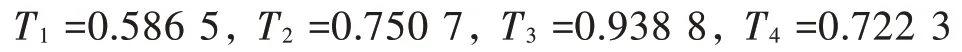
由式（5）得：

对S 计算结果进行排序，取max{S }为最优解方案，即该水域为三级，符合常理。

例3：与D⁃S证据理论进行比较，设某识别框架为，，对应证据的评价标准，如表4所示，实际传感器测量值为60，38，1.5，4.8，根据实测值进行基本概率分配，如表5所示。表6为两种方法融合结果对比。

表4 例3识别框架下评价标准

表5 例3识别框架下证据数据

表6 不同方法融合结果对比

分析表6中数据可知：当证据数小于等于3时，各证据表明识别结果为的可能性最大，与本文方法结果相同；当证据数为4时，D⁃S证据理论判断结果受基本概率分配影响较大，与事实相悖，不具备参考价值，而本文方法识别结果为，符合常理。为进一步比较两种方法，分别计算两种方法的区分度，如表7所示。

表7 两种方法的区分度

由表7可知，两种方法的区分度均达到了0.5以上，证据数为4时，采用本文方法的计算结果区分度达到了0.779 6，而D⁃S证据理论由于决策结果与事实相悖，失去可比性。

5 结 语

本文提出了一种基于距离矢量的多传感器信息决策算法。对多传感器信息决策模型做了简要介绍，从单属性与多属性决策角度分析了该决策方法原理，通过对单属性决策的纵向与横向运算将其扩展至多属性决策；定义了中心值向量、实际测量值向量以及支持度矩阵，其次，经归一化处理，得出优势度函数，规范化对决策结果进行排序，取值最大为最优解方案；最后，为方便算法评价优劣，定义了区分度函数。经仿真案例分析表明，本文方法在传感器信息决策中有良好的决策效果，且区分度均达到了0.5以上，通过与D⁃S证据理论比较可知，本文方法可有效避免D⁃S证据理论在决策时出现相悖的情况，相对于在决策过程中需对初始传感器数据进行概率赋值，具有明显优势。