基于V-I轨迹颜色编码的非侵入式负荷识别方法

解 洋，梅 飞，郑建勇，，高 昂，李 轩，沙浩源

（1. 东南大学网络空间安全学院，江苏省南京市 211102；2. 河海大学能源与电气学院，江苏省南京市 211100；3. 东南大学电气工程学院，江苏省南京市 210096）

0 引言

根据中国提出的“碳达峰、碳中和”的发展要求，建设清洁低碳、安全高效的能源体系已经迫在眉睫。随着中国居民生活水平的提高，居民用电量在国民经济总用电量的占比不断增加。非侵入式负荷识别（non-intrusive load monitoring，NILM）技术能够分析用户的用电负荷并帮助居民制定合理的用电策略，实现电网用电的“削峰填谷”［1-3］。

当前，NILM 主要通过挖掘负荷特征，然后根据负荷的不同特征结合深度学习、神经网络等分类算法进行负荷的分类。文献［4］将负荷特征分为稳态特征和暂态特征，主要包括电压和电流波形、有功和无功功率、电流谐波、电压-电流轨迹（V-I轨迹）等，其中V-I轨迹被广泛采用。文献［5］从V-I轨迹中提取形状特征，分析不同形状特征所表征的物理特性，并采用层次聚类算法对提取的形状特征进行分类。文献［6］根据不同负荷内部电路的拓扑结构将负荷分为七大类，包括电阻性负荷、阻容性负荷、阻抗性负荷等，并根据不同负荷的类别对比分析了其对应的V-I轨迹之间的差异，从V-I轨迹中提取了一种快速计算负荷谐波的计算方法，并利用从V-I轨迹中提取的特征对负荷进行分类。文献［7］采用反向传播（back propagation，BP）神经网络和卷积神经网络（convolutional neural network，CNN）分别对负荷的功率和V-I轨迹进行特征的提取和融合，将融合后的复合特征导入分类器完成负荷的辨识。文献［8］对比分析V-I轨迹与其他高频特征的辨识效果，证明了V-I轨迹作为负荷特征的优越性，并研究了不同采样频率对负荷辨识的影响。文献［9］采用格莱姆矩阵的方法构建带有颜色区分的负荷标识。文献［10］采用迁移学习的方法对负荷进行辨识，为了避免迁移学习中负迁移现象和增加负荷V-I轨迹的唯一性，文章结合其他负荷特征对V-I轨迹进行了颜色编码。在基于V-I轨迹的负荷辨识方法中，由于V-I轨迹是由归一化的电压值和电流值绘制的，从原理上无法表征用电器功率的大小。因此，采用单一的V-I轨迹既不能有效区分V-I轨迹相似但功率存在差异的负荷［10］，又不能有效区分V-I轨迹相似且功率相近的负荷，而且对于大量采用V-I轨迹进行识别其模型的训练需要占用较多计算资源。

基于此，本文提出了一种基于V-I轨迹颜色编码的NILM 方法。首先，提取负荷的有功和无功功率作为特征标识并采用K-means 聚类算法完成第1阶段的识别。然后，对第1 阶段未分类成功的负荷，构建该类负荷的V-I轨迹特征并对V-I轨迹做进一步的颜色编码，采用AlexNet 神经网络对编码后的V-I轨迹进行训练和分类以完成第2 阶段的识别。此方法减少了V-I轨迹训练量并节省了计算资源，同时，也涵盖了负荷的功率特征，对于V-I轨迹相似的负荷通过颜色编码增加了V-I轨迹的唯一性，提高了识别的准确率。通过公共数据集PLAID 和WHITED 对论文所述方法进行验证，证明了所提方法的有效性。

1 第1 阶段识别

1.1 功率特征的获取

第1 阶段的识别针对负荷的功率进行分类，其中功率包含有功和无功功率。有功功率可直接通过数据采集装备获取的电压、有功电流值计算。而无功功率需要事先得到负荷的无功电流量。

根据Fryze 理论［11-12］，电流i(t)的计算公式为:

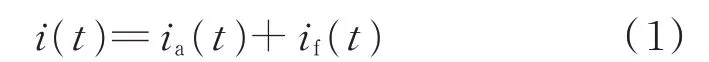
式中:ia(t)为负荷的有功电流，计算式如式（2）所示；if(t)为负荷的无功电流。

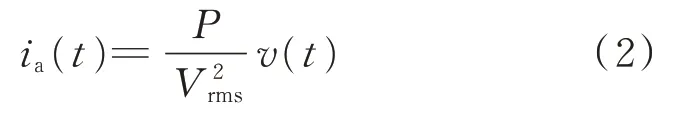
式中:P为负荷在稳定阶段的有功功率；v(t)为电压测量值；Vrms为电压的有效值。

因此，无功电流的计算公式为:

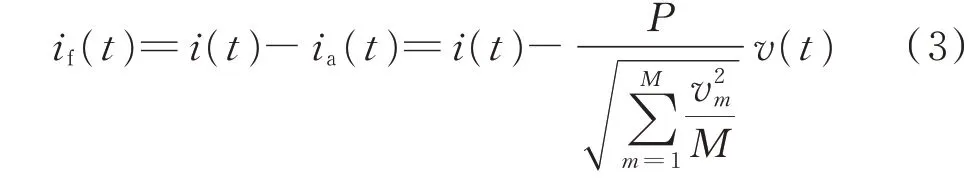
式中:m为稳定周期内从第1 个计量点开始的第m个点；M为稳定周期内采集的数据个数；vm为第m个点的电压值。

在负荷稳定后，通过对采集的离散电压、电流数据做积分运算来获取负荷的有功功率P和无功功率Q，其计算公式分别为:

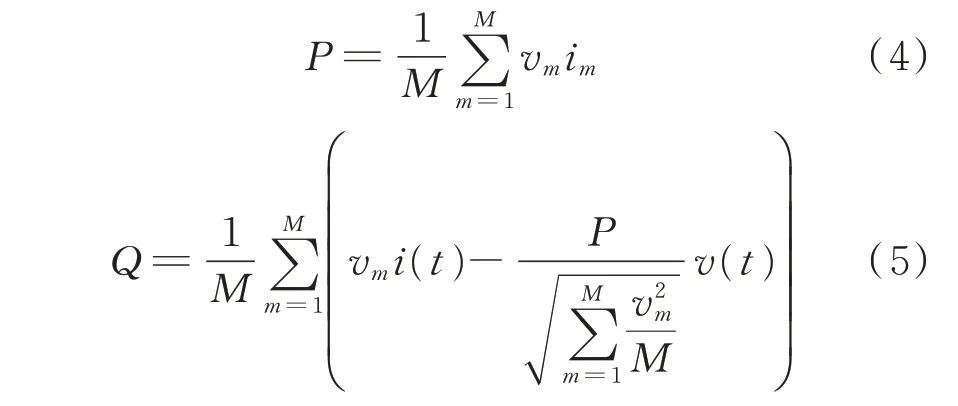
式中:im为第m个点的无功电流。

1.2 基于功率特征的初步分类

本文采用K-means 聚类算法进行初步分类，将负荷的有功和无功功率作为聚类的质心，对于功率特征存在差异的负荷能够有效进行区分。

K-means 聚类算法属于无监督聚类算法，因为算法结构简单、运算周期较短、聚类效果明显等优点被广泛应用。K-means 算法的主要思想为:给定一个样本集，按照样本之间的距离大小，将样本集划分为K个聚类中心（也称为K个族）。聚类效果的评价标准为:聚类中心的样本点之间的距离小，聚类中心与中心之间的距离尽可能大［13］。将其距离的平方误差作为目标函数E，即

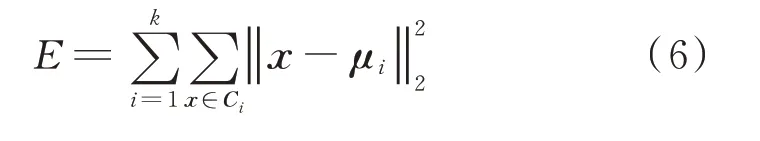
式中:k为族的个数；x表示当前点的位置；Ci表示第i个族；μi为Ci的均值向量，其数学表达式如下。

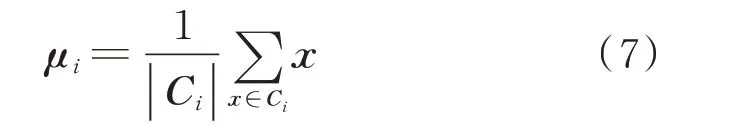
通过迭代运算使目标函数E取得最小值。

2 第2 阶段识别

在第1 阶段分类所产生的类群中，对于具有“非唯一”性的类群说明其功率特征具有相似性，仅采用功率特征不足以对其进行有效区分，需要进行第2阶段的分类。第2 阶段分类主要通过构建V-I轨迹，对V-I轨迹做颜色编码处理，并将处理后的V-I轨迹作为第2 阶段分类的标识。

2.1V-I轨迹的构建

V-I轨迹作为负荷分类的重要标识，其构建需要有足够的采样频率方能满足要求。文献［8］采用V-I轨迹作为负荷分类的标识，并证明了当采样频率大于4 kHz 时具有良好的识别效果。本文使用数据集PLAID 和WHITED 的采样频率分别为30 kHz和44 kHz，满足V-I轨迹作为负荷标识的要求。V-I轨迹的构建方法总结如下［14-15］。

1）提取负荷运行稳定后的一个完整周期内的所有电压和有功电流数据，然后对提取的数据进行归一化处理。其计算公式为:

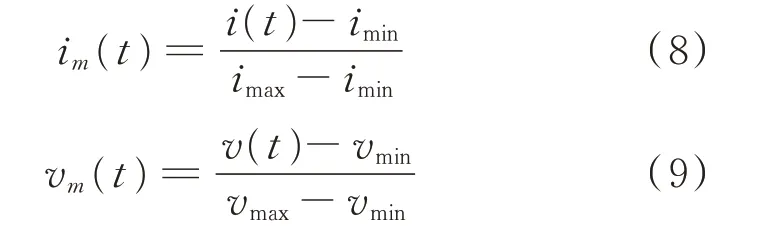
式中:imin和imax分别为一个周期内电流的最小值和最大值；vmin和vmax分别为一个周期内电压的最小值和最大值。

2）设置V-I轨迹图的分辨率。假设分辨率为n×n，则将归一化的电压、电流数据分别乘以n并进行向下取整处理，得到一组小于等于数值n的电压、电流数据（imn和vmn）。

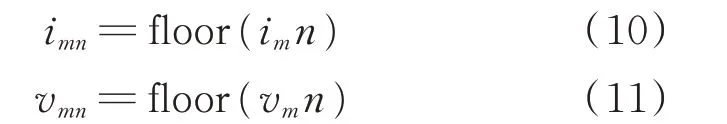
式中:floor(·)表示向下取整函数。

3）创建一组n×n的零矩阵，在一个完整周期内从第1 行开始取值直至最后1 行，其中每1 行的imn和vmn分别对应零矩阵中的第m行和第n列，并将该位置的0 值赋值为1，如此重复直至结束即可得到该负荷的V-I轨迹图。

典型负荷稳定运行后的电压波形和电流波形如附录A 图A1 所示，经过变换之后其V-I轨迹如附录A 图A2 所 示。

虽然V-I轨迹能够区分大部分负荷，但是存在某些负荷其V-I轨迹也很难被神经网络所区分。文献［5］详细分析了V-I轨迹的不同特性所表征负荷的不同物理信息，其中主要包含8 种特性，分别为:不对称性、循环方向、封闭区域面积大小、中线斜率、交叉点的数量、中段斜率、左右部分的面积、中段峰值。这些特征所表征的物理特性有负荷电流波形的对称性、电压与电流之间的相角关系（超前还是滞后）、电压与电流之间夹角的大小、电流波形的谐波含量等等。因此，负荷的V-I轨迹在一定程度上能够作为区分不同负荷的重要标识。

在实际的V-I轨迹中，上述8 种特征不足以完全区分所有的负荷，因此，需要增加V-I轨迹的特征量以提高其不同负荷的V-I轨迹的可区分性。

2.2 基于V-I轨迹的颜色编码

为了将负荷的识别标识尽可能涵盖其特性参数，本文采用无功功率、电压v(t)与有功电流ia(t)变化率的比值，以及负荷稳定运行周期之前V-I轨迹图对应像素点的变化比值的平均值作为RGB 颜色空间的Red 矩阵通道、Green 矩阵通道和Blue 矩阵通道（下文简称R 通道、G 通道和B 通道），其中每一个通道均为与V-I轨迹相同像素个数的n×n矩阵，其颜色编码的方法总结如下。

1）R 通道的构建

通过计算负荷的无功功率Q作为RGB 颜色空间中R 通道，即

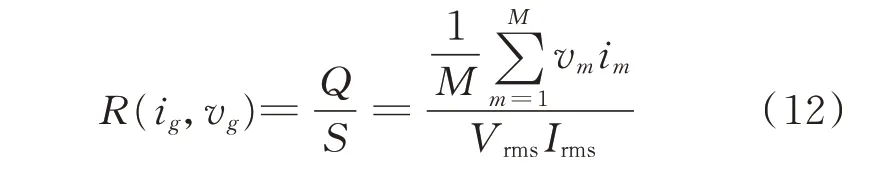
式中:R(ig，vg)表示在Red 矩阵中第ig行第vg列的R值；S表示视在功率；Irms表示电流的有效值；g=1，2，…，n。

2）G 通道的构建

通过对负荷稳定周期内的电压、无功电流的变化率进行可视化研究发现，不同的负荷在稳定周期内电压以及电流的变化率存在一定差异，因此，本文将其作为V-I轨迹特征中进行颜色编码的G 通道数据。本文定义G 通道中第g个点的G值为:

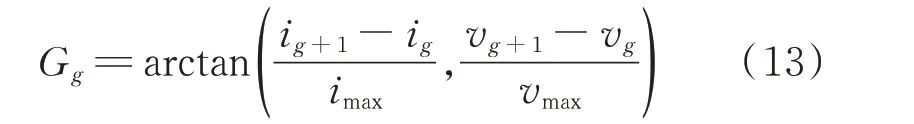
式中:imax=|i(t)|max和vmax=|v(t)|max分别为在稳定周期内电流绝对值和电压绝对值的最大值。

3）B 通道的构建

在负荷开启后，需要经过一段时间非稳定阶段然后进入稳定运行阶段，在非稳定阶段其V-I轨迹特征与稳定运行后的V-I轨迹特征有一定差异，不同的负荷其非稳定运行阶段V-I轨迹特征也是表征不同负荷的一种重要特性。为了将负荷非稳定运行阶段的特性融入负荷标识中，本文将非稳定周期的V-I轨迹的平均值作为RGB 颜色空间中的B 通道。其B值的计算公式可表述为:

式中:Z表示负荷在非稳定运行阶段的周期数；Wz表示第z个非稳定阶段的V-I轨迹特征中对应像素点的值。

为了对颜色编码中RGB 颜色空间的R 通道、G通道和B 通道构建后有更直观描述，本文采用灰度图对其进行可视化。本文采用PLAID 数据集中第10 个CSV 文件的数据做可视化示例，其编码过程如图1 所示。

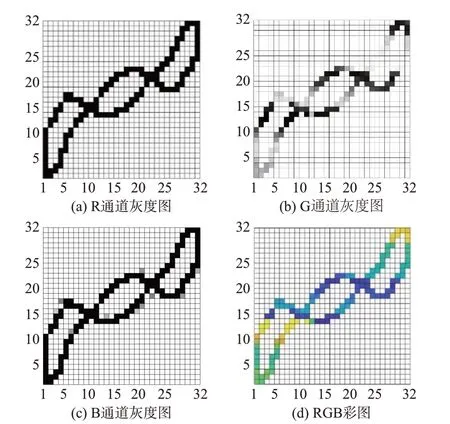
图1V-I轨迹特征颜色编码过程Fig.1 Color coding process ofV-Itrajectory characteristics

图1（a）为对R 通道矩阵的可视化结果，由于负荷稳定运行后其无功功率以及视在功率都是稳定值，所以R 通道灰度图中每个像素点的值均相同。图1（b）为对G 通道的可视化结果，可以看出G 通道的像素值具有很高的辨识性，这是因为不同负荷其运行周期内不同时刻无功电流的变化率存在很大的差异性。图1（c）为对B 通道的可视化结果，由于负荷开启后从非稳定运行阶段到稳定运行阶段的V-I轨迹会发生一定偏移，从图1（c）可以看出这种微小的变化。图1（d）为对R 通道、G 通道以及B 通道合成之后的显示效果。

3 神经网络结构设计及分类方法

3.1 神经网络结构

第2 阶段的分类模型采用AlexNet 神经网络，AlexNet 神经网络本质上属于卷积神经网络，经过优化改进对于图片识别和分类有着出色的性能［16］。表1 为经过本文调整之后的模型结构及内部运算过程。输入的图片经过卷积层和池化层的转化之后进入全连接层，该神经网络包含3 个全连接层，第1 个全连接层连接有4 096 个神经元，经过第2 个全连接层后产生4 096 个向量并作为最后一个全连接层的输入，最后一个全连接层生成的向量个数等于待分类的负荷种类数。

表1 中:11×11（48）表示11×11 尺寸的48 个核函数，下同；Ks表示卷积核的大小；s表示步长。原始模型包含5 个卷积层和3 个全连接层，全连接层3 作为最后的输出层有1 000 个神经元，也就是原始的该模型有1 000 种分类结果，输入图像的大小也必须为227×227×3。在待分类图片进入神经网络后，经过不同卷积层被不同大小的卷积核做卷积运算，图片的大小也随之改变。随后，经过全连接层输出到Softmax 函数，并进入最后的输出层，完成分类。

表1 神经网络的结构及运算过程Table 1 Structure and operation process of neural network

原始的AlexNet 模型不能满足PLAID 数据集的分类要求，本文通过对AlexNet 神经网络进行调整，适应对负荷辨识的要求。对PLAID 数据集进行分析，其中包含11 类负荷类别。令网络的全连接层输出神经元的个数等于负荷的类别数，并调整卷积层中卷积核和步长来适应待分类图片的大小，卷积过程的输出遵循的计算规则参考文献［17］。

3.2 识别流程

本文的负荷识别流程如图2 所示，其中包含数据采集、数据预处理、聚类运算、V-I轨迹特征的颜色编码、运用AlexNet 神经网络对负荷特征进行分类等步骤，可总结为2 个主要部分:初步识别和精细化识别。

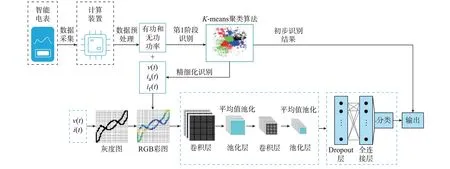
图2 负荷识别流程Fig.2 Load monitoring process

初步识别:大部分负荷的功率具有一定差异，因此，可将负荷的有功和无功功率作为负荷初步识别的特征标识。本文采用K-means 聚类算法对负荷的功率进行聚类运算，将负荷的功率作为聚类中心进行聚类运算，并将未能正确分类的负荷做进一步精细化分类。

精细化识别:对初步识别中“非唯一”的类群进行第2 步分类。首先，提取其稳定周期内的电压、有功电流进行V-I轨迹特征图的构建；然后，将无功功率、稳定周期内电压和无功电流变化率的比值，以及非稳定周期的V-I轨迹像素的平均值作为RGB 颜色空间的3 个颜色通道；最后，将经过颜色编码后的V-I轨迹特征图作为AlexNet 神经网络的输入并进行分类，最终实现精细化分类效果。

4 算例分析

在实际算例中，采用基于Python3.8 平台tensorflow2.0 的深度学习框架，并对原始AlexNet 神经网络进行改进，如上文所述。硬件平台为Intel Core i5-10210U CPU、16 GB RAM。 数 据 集 为PLAID 和WHITED，PLAID 的采样频率为30 kHz，该数据集记录了美国宾夕法尼亚州55 个家庭用户的用电数据，其中包含有11 种不同电器1 793 组电压、电 流 数 据［18］；WHITED 的 采 样 频 率 为44 kHz，该数据集记录了全世界不同国家地区的用户用电数据，其中包含了54 种不同电器1 259 组电压、电流数据［19］。

本文首先采用负荷的功率特征进行初步分类，然后对初步分类中的“非唯一”类的负荷进行第2 阶段的分类。随后，从识别准确率和训练所用时间的角度综合对比本文所提分类方法和其他分类方法，验证本文所提方法的优越性。

4.1 PLAID 数据集

4.1.1 PLAID 数据集的第1 阶段识别

以负荷的有功和无功功率作为负荷聚类的质心，本文采用K-means 聚类算法对负荷进行初步分类，其中K的取值为负荷类型的个数，在PLAID 数据集中有11 种不同类型的负荷，因此K=11。在距离坐标中，采用有功功率P的大小表征x坐标、无功功率Q的大小表征y坐标，其分类结果如表2所示。

通过观察表2 发现，“唯一”类的有C7、C8、C9、C10，但是C7 类空调也出现在其他类（如C4 类）中，C11 类洗衣机出现在C1 类中，因此第1 步真正分类成功的只有C9 类加热器，其余电器均为“非唯一”类，需要将其作为第2 步待分类的电器。

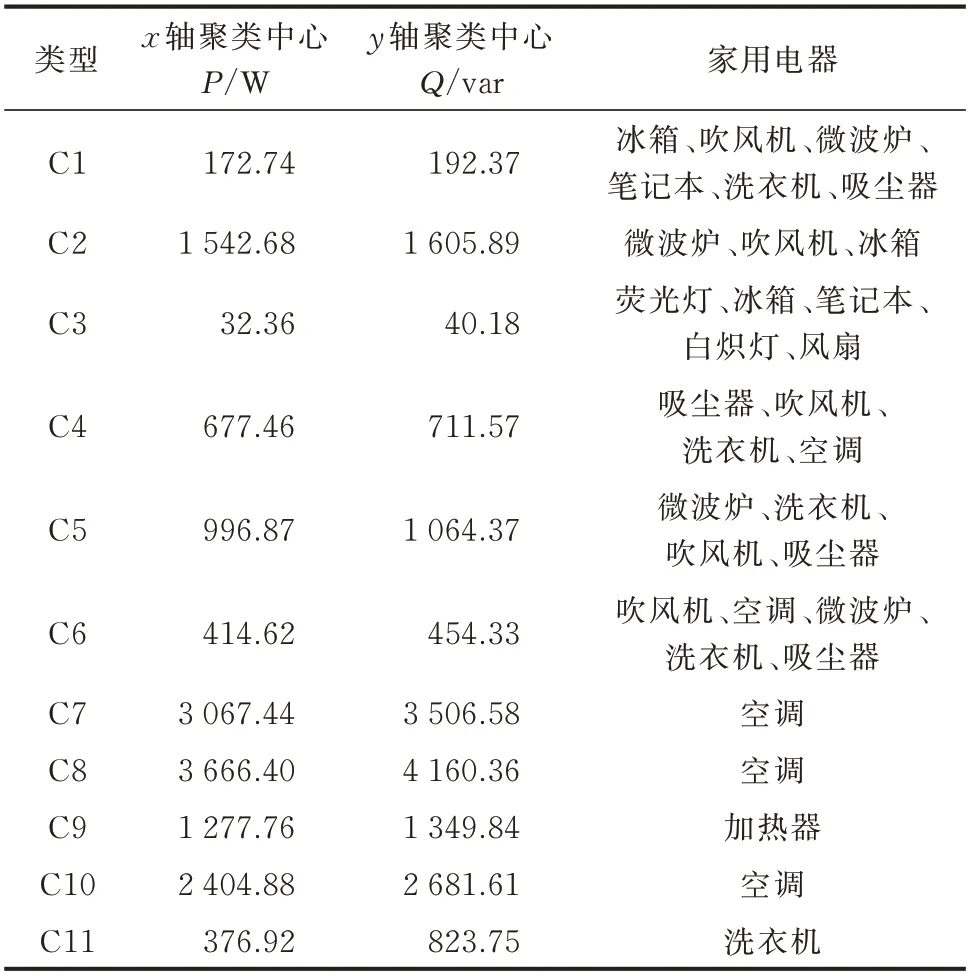
表2 PLAID 数据集的初步分类结果Table 2 Preliminary classification results of PLAID dataset

4.1.2 PLAID 数据集的第2 阶段识别

第2 阶段识别的第1 步是对负荷V-I轨迹进行构建，本文采用的V-I轨迹矩阵的大小为32×32，即n取值为32。构建完成后如附录A 图A3 所示，依次为空调、荧光灯、电风扇、冰箱、吹风机、加热器、节能灯、笔记本、微波炉、吸尘器、洗衣机。将构建完成后的V-I轨迹特征图的大小进行变换以适应AlexNet神经网络输入要求，通过批量调整后，V-I轨迹特征图由656×873×3 转换成227×227×3。调整模型的初始学习率、迭代次数、激活函数等相关参数如附录A 表A1 所示。经过相关参数调整之后，将1 793 个电器随机分成70%份额和30%份额分别作为神经网络的训练集和测试集，其训练的过程如附录A 图A4（a）所示。

为了更加全面地分析该方法的分类结果，而不仅仅使用分类准确率来评判，本文采用混淆矩阵对分类的结果做评判。通过对数据的可视化分析，上述分类后的混淆矩阵如图3 所示。图中的数字代表当前样本数量，黑色百分数代表当前样本数量对于总样本数量的占比，红色百分数代表识别错误率。其评价指标Pre代表准确率（如图3 中最后一列绿色百分数所示），Rre代表召回率（如图3 中最后一行绿色百分数所示），Fscore代表准确率和召回率的调和平均评估指标，计算公式分别如下［20-21］。

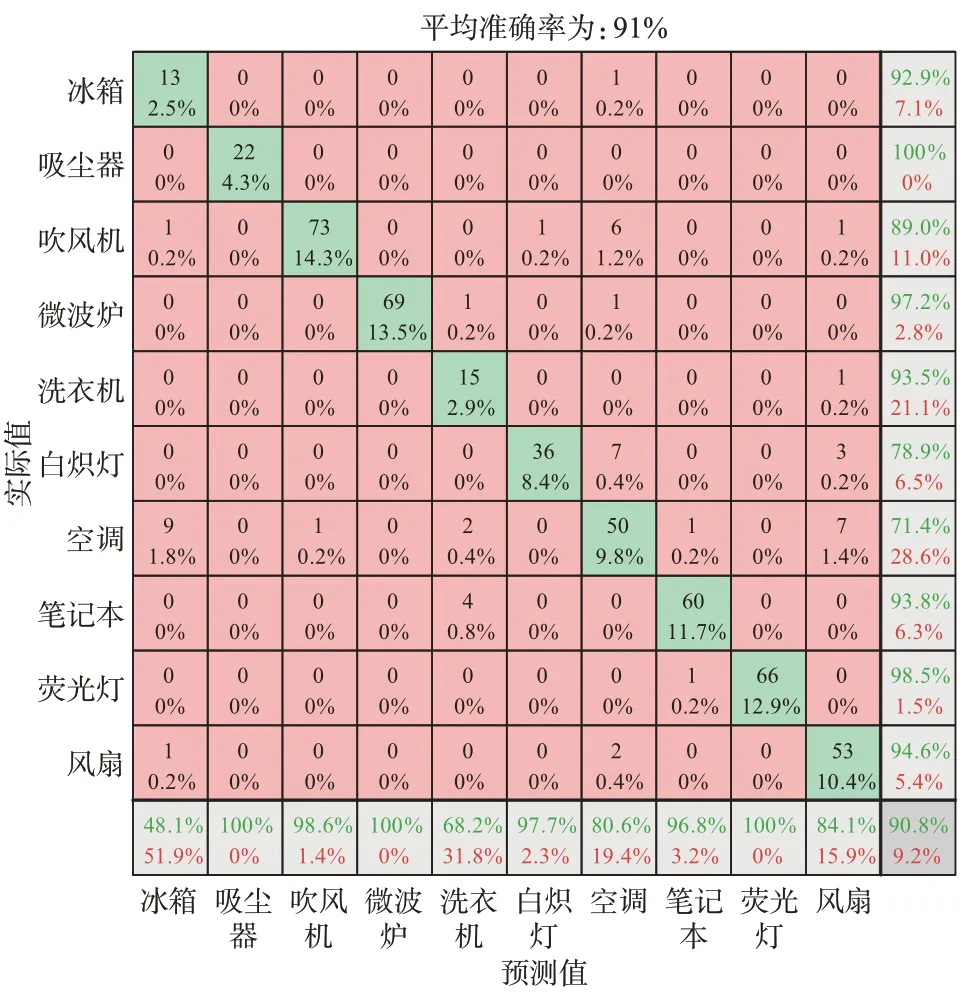
图3 基于V-I轨迹的第2 阶段分类结果Fig.3 Classification results of the second stage based onV-Itrajectory

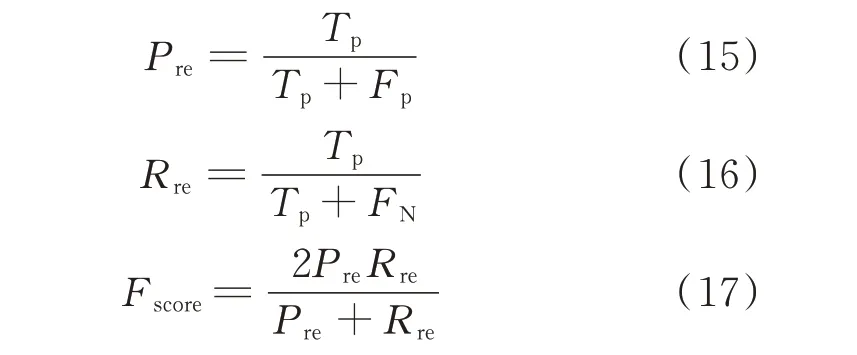
式中:Tp为实际上是正类，同时被预测为正类的数量；Fp为实际上是负类，但是被预测为正类的数量；FN为实际上是正类，但是被预测为负类的数量［21］。

通过观察该混淆矩阵发现，白炽灯和空调的识别准确率均低于80%。由于该分类结果是基于第1步K-means 分类之后的，为了分析原因，将这11 类负荷全部通过V-I轨迹特征进行第2 阶段识别，其识别结果如附录A 图A5（a）所示。其中，加热器、空调、风扇、洗衣机等识别准确率低于平均值，结合这些负荷的V-I轨迹特征进行分析，发现这些负荷的V-I轨迹都呈现一定相似性。为此，本文结合负荷的其他物理量对V-I轨迹进行颜色编码，以增加负荷的唯一性，经过编码之后其V-I轨迹如附录A 图A6 所示。观察发现，尽管这几类负荷的V-I轨迹的形状特征较为相似，但是经过颜色编码之后其相同图形区域的颜色存在明显差异，因此，可以预判经过颜色编码后的负荷标识能够发挥更好的分类效果。

将颜色编码后的V-I轨迹特征图的大小进行处理，然后导入AlexNet 神经网络中进行分类。为了将2 种分类效果进行横向比较，神经网络的参数设置完全与前述神经网络的参数相同，其运算过程如附录A 图A4（b）所示，经过相同次数的迭代运算之后，这11 类负荷的分类结果如附录A 图A5（b）所示，经过初步分类之后的10 类负荷的分类结果如图4 所示。通过观察该混淆矩阵，可以看出经过颜色编码之后的整体识别率均有所提升，分别从91%提升至94%和从87%提升至92%，且V-I轨迹特征形似的几类负荷的识别准确率提升更为显著。

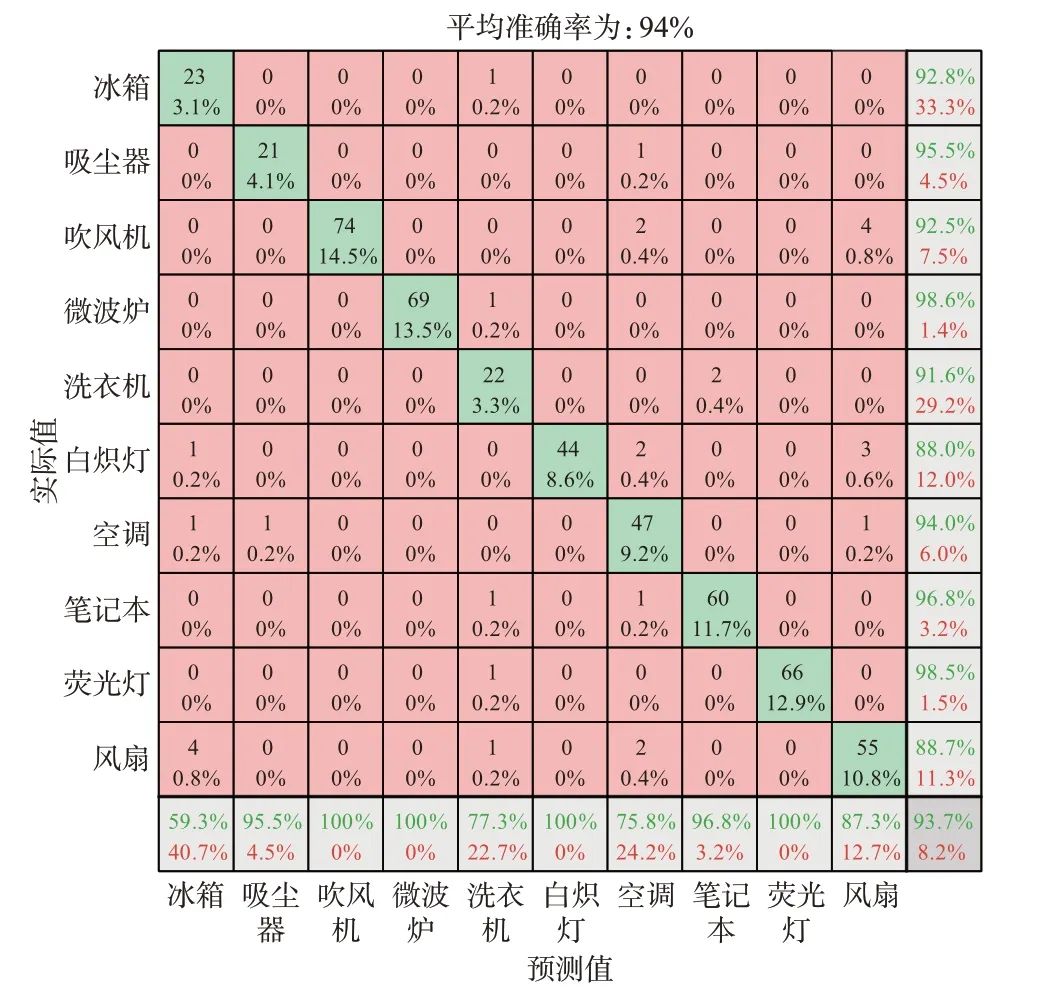
图4 基于V-I轨迹颜色编码的第2 阶段分类结果Fig.4 Classification results of the second stage based onV-Itrajectory color coding

4.2 WHITED 数据集

4.2.1 WHITED 数据集的第1 阶段识别

为了与PLAID 数据集进行横向对比，本文截取相同类型的11 种负荷，采用同样的方法对WHITED数据集进行第1 阶段分类，分类结果见表3。

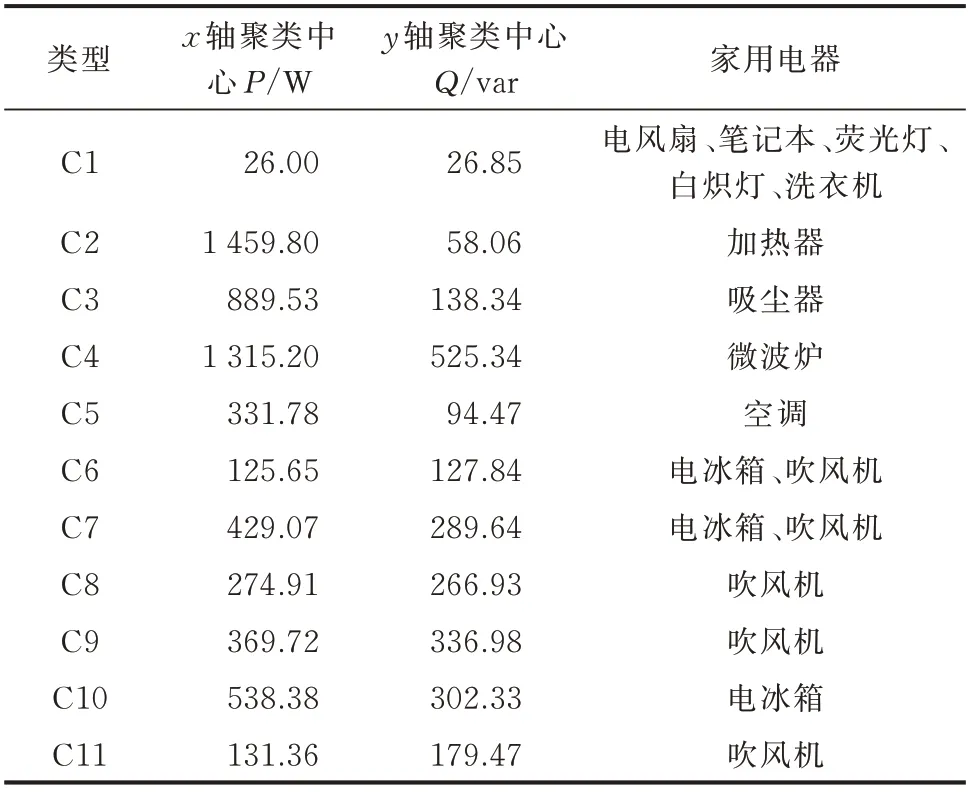
表3 WHITED 数据集的初步分类结果Table 3 Preliminary classification results of WHITED dataset

观察表3 发现，“唯一”类的有C2、C3、C4、C5（加热器、吸尘器、微波炉、空调），相较于PLAID 数据集，WHITED 数据集具有明显的功率差异，在第1 阶段识别中就可以区分较多的负荷种类。因此，在第2阶段的识别中需要训练和分类的负荷大大减少。

4.2.2 WHITED 数据集的第2 阶段识别

经过第1 阶段的识别之后，对分类结果中的“非唯一”类的负荷进行第2 阶段分类。通过分析表2可知，需要进行第2 阶段分类的负荷有电风扇、笔记本、荧光灯、白炽灯、洗衣机、吹风机、电冰箱这7 类。采用相同方法对7 类负荷进行V-I轨迹构建，构建后的V-I轨迹图如附录A 图A7 所示，并将生成的V-I轨迹图的大小调整至规定尺寸，由于第2 阶段分类的负荷只有7 类，需要将网络的全连接层输出神经元的个数调整为负荷的类别数7。经过相同次数的迭代和训练之后，其分类结果的混淆矩阵见图5。

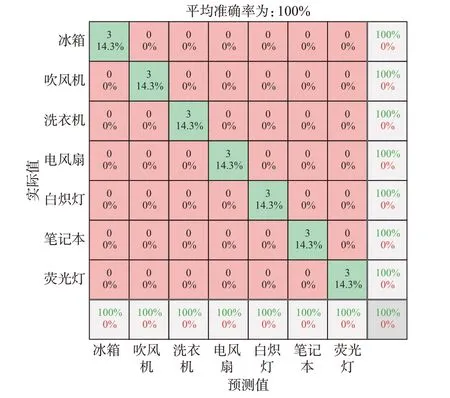
图5 WHITED 数据集的第2 阶段分类结果Fig.5 Classification results of the second stage of WHITED dataset

使用V-I轨迹和经过颜色编码之后的V-I轨迹在第2 阶段识别中都有100%的识别准确率。

4.3 分析与讨论

为了进一步验证本文方法的优越性，针对相同的数据集运用不同的神经网络和训练模型做对比分析和评价，标价指标为识别准确率和识别过程中计算所用时间。

在PLAID 数据集中，不同负荷的功率特征差异不大，仅仅采用功率特征不能对其进行有效分类。同时，在第2 阶段识别中发现某些负荷的V-I轨迹特征差异较小，导致此类负荷的识别准确率不高，在对原始的V-I轨迹进行颜色编码之后作为新的负荷标识有效地提高了其识别准确率。为了更加直观地对2 种特征的优劣进行评价，可使用主成分分析法（PCA）提取模型中的特征向量并投影至二维平面进行观察［22］，其特征分布如图6 所示，图6（a）为原始VI轨迹二维投影，图6（b）为经过颜色编码的V-I轨迹二维投影。对比可以看出，经过颜色编码之后的V-I轨迹其不同负荷的特征向量之间的距离相对原始V-I轨迹更远，说明经过颜色编码之后的V-I轨迹相较于原始V-I轨迹在识别的模型中有更明显的区分性。

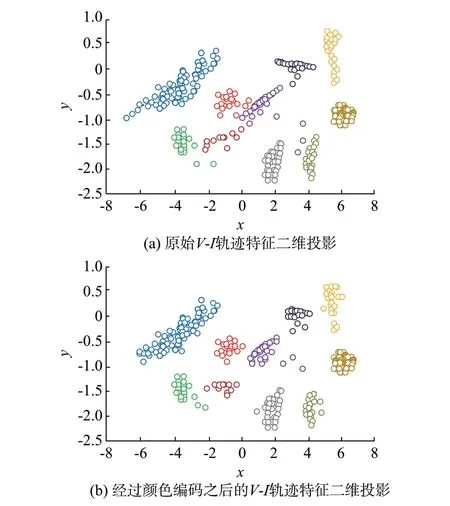
图6 提取特征的PCA 二维投影Fig.6 Two-dimensional projection of PCA for characteristic extraction

在WHITED 数据集中，不同负荷的功率特征具有一定的差异性，采用K-means 聚类算法对功率进行聚类能够识别部分负荷，在一定程度上减少了V-I轨迹构建和神经网络训练的所用时间。这部分算例中采用V-I估计和颜色编码的V-I轨迹特征进行识别的准确率都为100%，主要差异体现在采用本文方法能够有效节省计算时间。

为了综合对比不同负荷特征和分类模型在识别准确率和计算所用时间2 种指标下的性能表现，以及探究本文所提分类算法对于这2 种性能指标的提升由何种因素引起，对比实验中引入了文献［7］和文献［9］的负荷特征和分类算法。下面对不同的分类算法进行计算验证，本文在同一硬件平台下对PLAID 和WHITED 数据集进行了全面计算和记录，其结果如表4 所示。表中:SVM 表示支持向量机；RBFNet 表示径向基函数神经网络；LeNet-5 表示一种经典的卷积神经网络。

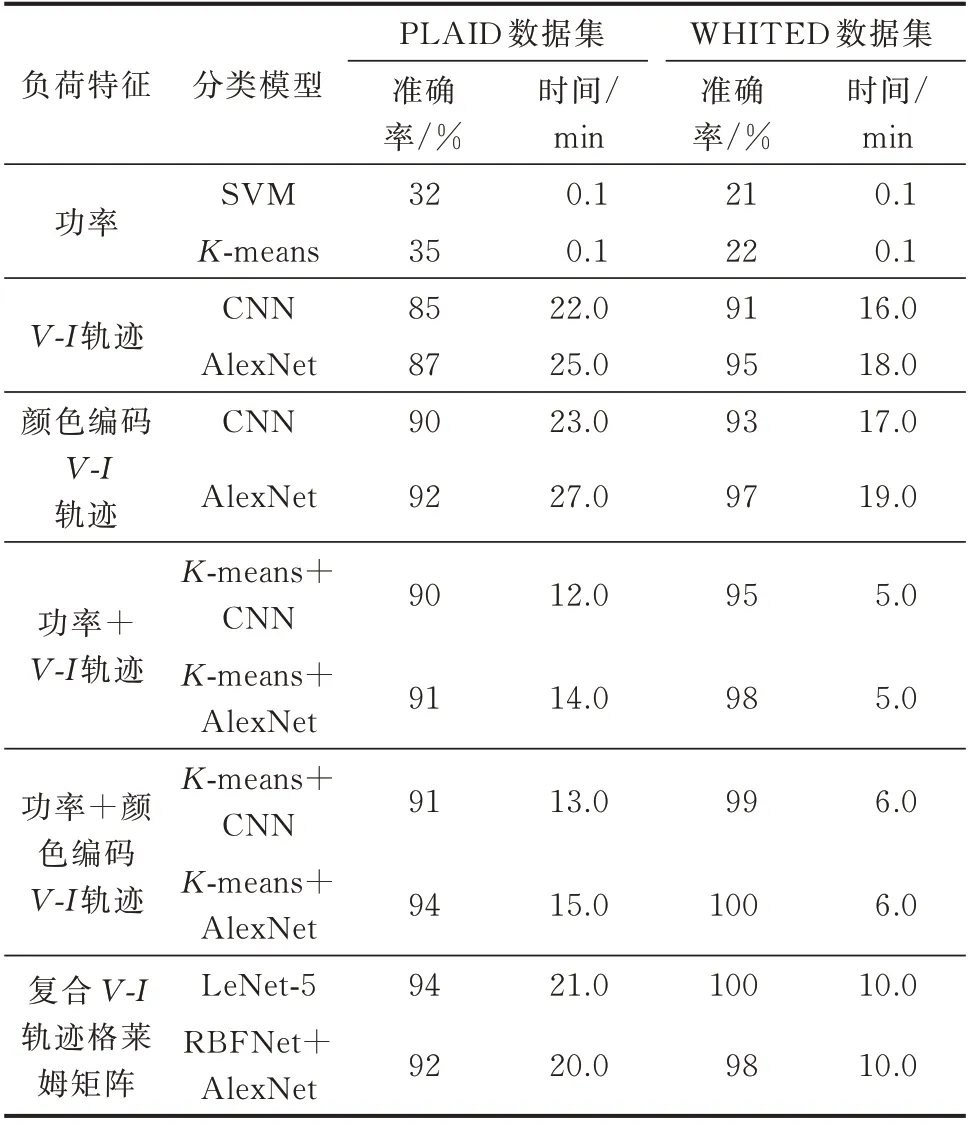
表4 不同算法分类能力对比Table 4 Comparison of classification capabilities of different algorithms

其中复合V-I轨迹为文献［7］所采用的方法，该方法采用特征融合将负荷的V-I轨迹特征和功率特征进行融合组成复合特征，该特征虽包含了负荷的功率特性，弥补了V-I轨迹丢失功率特征的缺点，但是下一步神经网络需要对全部的样本进行训练和分类，需要占用较多的计算资源，所花费的计算时间相对较长。格莱姆矩阵为文献［9］所采用的方法，该方法采用格莱姆矩阵对负荷的特征进行颜色编码，采用的颜色编码的物理信息均为负荷在稳定周期内的信息，并未包含非稳定周期的物理特性，且在采用格莱姆矩阵进行颜色编码时，矩阵中对应的每个元素都需要进行一次运算，相对于V-I轨迹而言，V-I轨迹仅取规格化的参数数据，计算量相对较小。另一方面，相较于本文的颜色编码方法，其所包含的信息量相对较少，因此，在识别准确率和计算所用时间上本文所提方法均在一定程度上有所提升。

从表3 可以看出，仅采用功率特征进行分类识别的准确率不高，但是计算时间相对较少。在采用V-I轨迹作为特征时，传统CNN 的训练模型中相对于AlexNet 神经网络没有基于图片分类做针对性优化调整，识别的准确率相对AlexNet 神经网络较低，但是分类时间相对较少。这是因为AlexNet 神经网络中增加了卷积层数量和神经元个数，并且在输入前端需要对待分类图片的尺寸进行计算调整［12］。以相同的分类模型进行训练，将未经过颜色编码的V-I轨迹和经过颜色编码的V-I轨迹的识别率进行对比可知，经过颜色编码之后的V-I轨迹的识别准确率明显提升。

本文完整的识别流程为K-means 聚类算法和神经网络训练相结合的形式。第1 步采用K-means 聚类算法对负荷的功率特征进行聚类，能够筛选出部分负荷从而降低了第2 步神经网络待分类的样本数量，而且K-means 聚类算法具有识别效率高、占用运算资源少等优点，因此有效减少了计算所用时间。第2 步首先对V-I轨迹进行颜色编码，然后采用神经网络对编码后的V-I轨迹进行训练和分类，经过编码后的V-I轨迹包含了负荷在非稳定周期内的物理特性，在一定程度上提高了识别准确率。本文结合两者的优点设计出的负荷识别方法能够达到快速、准确的分类效果。

5 结语

本文提出了一种非侵入式负荷分类方法，该方法首先运用K-means 聚类算法对负荷进行初步分类，然后采用经过颜色编码后的V-I轨迹特征对其做进一步的精细化分类。该分类方法结合了Kmeans 算法的高效性和AlexNet 神经网络的高精度，在提高识别准确率的同时也减少了分类所用时间。采用NILM 公共数据集PLAID 和WHITED 进行实例分析，并对比分析不同负荷特征和不同分类模型下的计算准确率和所用时间2 种指标，验证了本文所提方法的有效性，对NILM 的进一步研究有重要意义。

本文在撰写过程中得到国网江苏省电力有限公司2019 年科技项目（J2019027）资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。