一种耦合谐振电感IPOP型双谐振LLC变换器*

田 健, 徐玉珍

0 引 言

LLC变换器因其具有高传输效率、高功率密度、高集成化等优点,目前广泛应用于照明、通信等领域[1-2]。为了减小输入电流脉动,改善输入电流纹波,减小输入电容,进一步提高功率密度。文献[3-7]提出在两开关管两端分别并联谐振回路,形成双谐振LLC变换器。由于双谐振LLC变换器中的两个变压器二次侧绕组大多采用串联结构,故流经变压器二次侧绕组的电流就是负载电流,变压器体积较大,系统可靠性差[8-10]。变压器二次侧绕组并联连接的输入输出并联(Input-parallel Output-parallel,IPOP)型双谐振LLC变换器可以实现负载电流均分到两个变压器,从而减小变压器的体积,提高变换器功率密度。然而,由于实际制造工艺的差别,元器件存在一定的分散性,双谐振LLC变换器的两相谐振参数不可能完全一致,势必存在某一相模块所承受的电压或电流应力较大,严重的甚至导致开关器件损毁、电路瘫痪[11]。

本文提出一种具有自动均流特性的耦合谐振电感IPOP型双谐振LLC变换器。该变换器不需要额外检测元件及复杂的控制电路。首先研究该变换器的工作原理;接着采用基波分析法(First Harmonic Approximation,FHA)建立变换器等效电路模型,研究耦合谐振电感IPOP型双谐振LLC变换器的均流误差与输入电压、输出电流之间的关系,并与无耦合谐振电感IPOP型双谐振LLC变换器进行PSIM仿真对比,分析这两种谐振变换器的均流误差特性;最后搭建2.16 kW的实验样机,进一步验证理论研究的正确性。

1 耦合谐振电感IPOP型双谐振LLC变换器工作原理

一种具有自动均流特性的耦合谐振电感IPOP型双谐振LLC变换器如图1所示。该双谐振LLC变换器的输入、输出均为并联连接且谐振电感耦合。

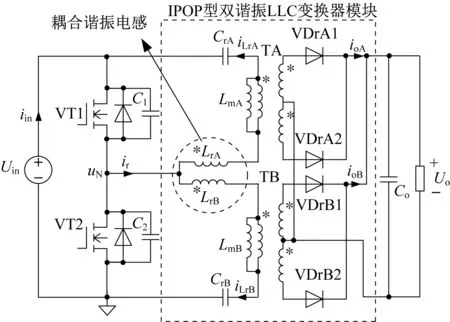
图1 一种具有自动均流特性的耦合谐振电感IPOP型双谐振LLC变换器

设双谐振LLC变换器的谐振腔分为A、B两相。其中,变压器TA、TB变比均为n;VT1、VT2为一次侧上、下两个开关管;VDrA1、VDrA2、VDrB1、VDrB2为二次侧整流管;LmA与LmB、LrA与LrB、CrA与CrB分别为A相与B相的励磁电感、谐振电感、谐振电容,其中LrA与LrB为耦合电感。为了减小两者之间的感量偏差,该耦合电感采用双线并绕。当A、B两相谐振电流出现偏差时,耦合电感器将产生感应电动势来抑制谐振电流的不平衡。

为了方便研究,假设变换器:

(1) 所有功率开关器件均为理想元件;

(2) 所有电感、电容和变压器均为理想元件;

(3) 输出滤波电容足够大,输出电压Uo恒定。

耦合谐振电感IPOP型双谐振LLC变换器以B相谐振参数LrB、CrB、LmB均正向偏大于A相谐振参数LrA、CrA、LmA为例,则A相谐振频率frA大于B相谐振频率frB。变换器的主要工作波形如图2所示。其中,ugs1、ugs2分别为MOS开关管VT1、VT2的驱动控制信号;iLrA、iLrB分别为A、B相的谐振电流;iin为输入电流;ioA、ioB分别为A、B相的输出电流。

图2 变换器主要工作波形

图2中,输入电流iin是连续的。该变换器具有12种工作模态,其中正、负半周对称,工作模态图如图3所示。

图3 工作模态图

模态1[t0～t1]:t0时刻前,开关管VT1处于截止状态,VT2处于导通状态。t0时刻,VT1、VT2关断,二次侧整流二极管VDrA2、VDrB1导通,导致变压器TA、TB的一次侧电压均被箝位在nUo,励磁电感LmA、LmB不参与谐振过程。谐振电感电流iLrA、iLrB为VT2的寄生电容C2充电,同时也为VT1的寄生电容C1放电。半桥中点电位uN上升至Uin,使得VT1可以零电压开通。

模态2[t1～t2]:t1时刻,半桥中点电位uN上升至Uin,VT1实现零电压开通。由于此时谐振电流iLrA、iLrB为负,由MOS开关管的源极流向漏极,因此MOS开关管VT1起到同步整流作用。二次侧整流二极管VDrA2、VDrB1导通,导致变压器TA、TB的一次侧电压均被箝位在nUo,励磁电感LmA、LmB不参与谐振过程。

模态3[t2～t3]:t2时刻,谐振电感电流iLrB过零,而后开始正向流过MOS开关管VT1,而iLrA仍为负,因此MOS开关管VT1仍起到同步整流作用。二次侧整流二极管VDrA2、VDrB1导通,导致变压器TA、TB的一次侧电压均被箝位在nUo,励磁电感LmA、LmB不参与谐振过程。

模态4[t3～t4]:t3时刻,谐振电感电流iLrA过零,而后开始正向流过MOS开关管VT1。二次侧整流二极管VDrA2、VDrB1导通,导致变压器TA、TB的一次侧电压均被箝位在nUo,励磁电感LmA、LmB不参与谐振过程。

模态5[t4～t5]:t4时刻,谐振电感电流iLrA等于励磁电感电流iLmA,而后励磁电感LmA参与到谐振当中,即LrA、CrA、LmA构成串联谐振。变压器TA一次侧不再向二次侧传递能量,二次侧整流二极管VDrA2截止。因为谐振频率frB小于谐振频率frA,所以在这个阶段谐振电感电流iLrB大于励磁电感电流iLmB,二次侧整流二极管VDrB1处于导通状态,导致变压器TB的一次侧电压均被箝位在nUo,励磁电感LmB不参与谐振过程。

模态6[t5～t6]:t5时刻,谐振电感电流iLrB等于励磁电感电流iLmB,而后励磁电感LmB参与到谐振当中,即LrB、CrB、LmB构成串联谐振。变压器TA、TB一次侧不再向二次侧传递能量,二次侧整流二极管VDrA2、VDrB1截止。这个阶段持续到t6时刻,开关管VT1关断。之后,电路进入下半个工作周期。

2 变换器均流特性分析

2.1 无耦合谐振电感IPOP型双谐振LLC变换器

理想情况下,变换器两相谐振参数完全对称。当两相参数不一致的情况下,以谐振电感Lr、谐振电容Cr、励磁电感Lm作为标准谐振参数,两相谐振参数变量如式(1)所示。其中A相的谐振参数等于标准谐振参数;而式(1)中a、b、c分别代表B相谐振电感LrB、谐振电容CrB、励磁电感LmB相对于标准谐振参数的偏差比例系数。

(1)

定义Uo、Po、Ro为两相的输出电压、总输出功率和总负载电阻。Uo、Po、Ro之间的关系为

(2)

PoA、PoB分别为A相与B相的输出功率。在稳态下,PoA与PoB将构成总输出功率Po。

Po=PoA+PoB

(3)

则每相谐振回路的等效负载电阻RoA和RoB可表示为

(4)

k定义为负载因子,即A相承担功率与总输出功率之比。输出功率PoA和PoB可以表示为

(5)

由式(4)和式(5)可得:

(6)

无耦合谐振电感IPOP型双谐振LLC变换器的FHA等效模型如图4所示。

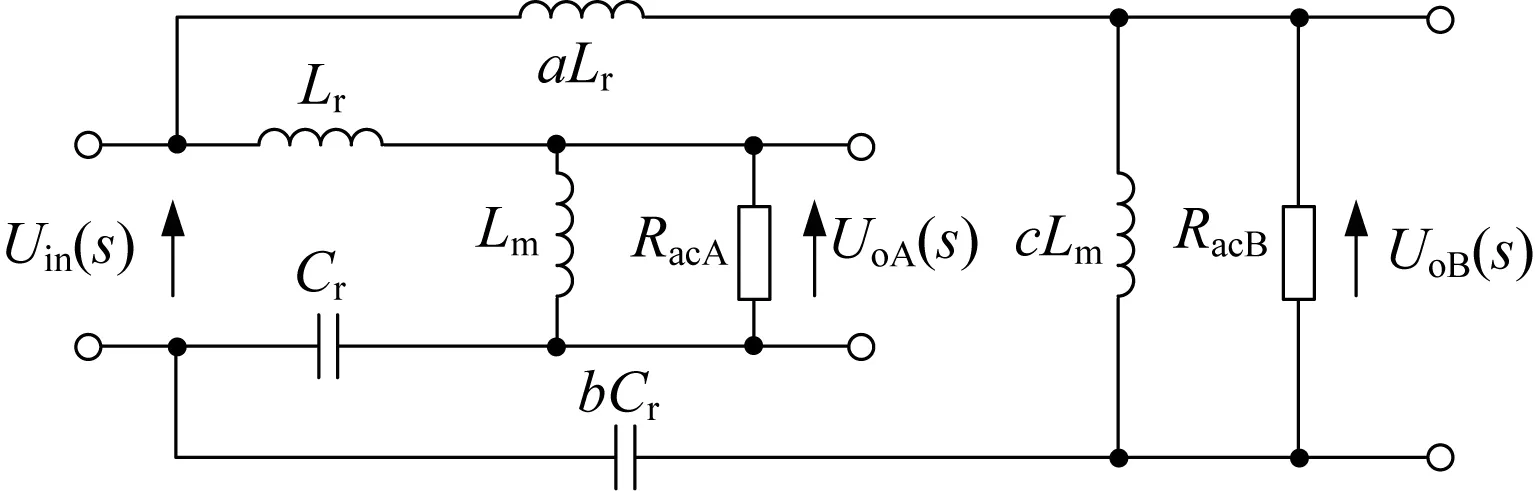
图4 无耦合谐振电感IPOP型双谐振LLC变换器的FHA等效模型

UoA(s)和UoB(s)是两相变压器一次侧的反射交流电压。一次侧等效交流电阻RacA和RacB可表示为

(7)

结合式(6)、式(7)可得:

(8)

由于两相LLC谐振变换器在输入侧和输出侧都是并联,因此稳态运行时,两相电压增益相同。交流电压UoA(s)和UoB(s)的大小相同,两者的关系表示为

|UoA(s)|=|UoB(s)|

(9)

根据图4的FHA等效模型,可以将UoA(s)和UoB(s)的传递函数表示为

(10)

结合式(8)、式(9)、式(10),可得负载因子k满足:

Ak2+Bk+C=0

(11)

其中,参数A、B、C表达式为

(12)

式中:a、b、c——B相谐振参数相对于A相的偏差比例系数;

Rac——总的等效交流负载电阻;

考虑一个三维定位的场景,该场景包含5个移动的传感器(N=4)和一个移动的未知目标,传感器的位置和速度分布如表1所示。用σ2表示测量噪声的功率,TDOA测量噪声的协方差矩阵为测量噪声的协方差矩阵为Qf=0.01Qt。用M表示蒙特卡洛运行次数,用xi表示第i次估计时的位置估计值,用 表示第i次估计时的速度估计值。使用均方根误差(RMSE)和偏差(bias)来评估定位性能,均方根误差和偏差的定义如下:

ω——一次侧半桥开关的角频率。

其中,

ω=2πfs

(13)

结合式(12)和式(13)可求得负载因子k。

(14)

其中,负载因子k∈(0,1)。当k介于0到1之间时,才是有效的。当k=0.5时表示负载功率被A、B两相平均分配。当k=0或k=1时则表示只有一相承担了全部功率,而另外一相输出的功率为0。

为了评估均流性能,定义δload为负载均流误差,即

(15)

定义δres为谐振均流误差为

(16)

式中:ILrA、ILrB——A、B两相谐振腔内的谐振电流均方根值。

2.2 耦合谐振电感IPOP型双谐振LLC变换器

由于谐振电感LrA、LrB并绕耦合,解耦后,每相谐振电感感量一致,均为(1+a)Lr/2。因此,耦合谐振电感IPOP型双谐振LLC变换器的FHA等效模型如图5所示。

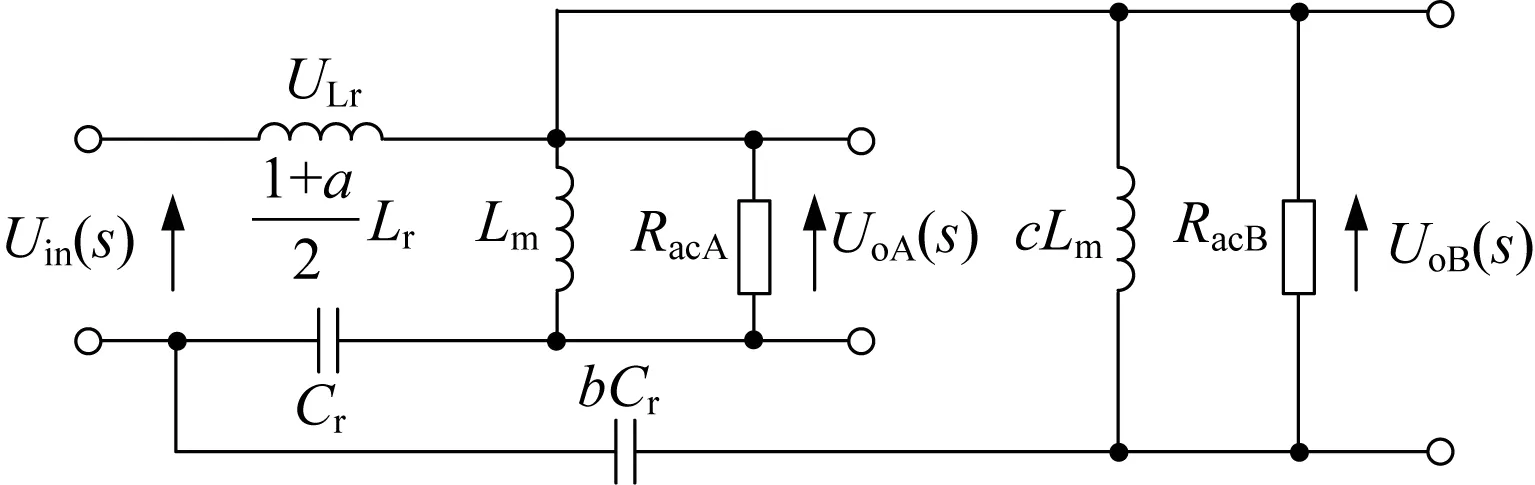
图5 耦合谐振电感IPOP型双谐振LLC变换器的FHA等效模型

根据图5的FHA等效模型,UoA(s)和UoB(s)的传递函数表示为

(17)

负载因子k仍然符合式(11)的二次方程,对于耦合谐振电感IPOP型双谐振LLC变换器,系数A、B、C表达式为

(18)

结合式(11)和式(18),可求出在不同输入电压和负载条件下,耦合谐振电感IPOP型双谐振LLC变换器的负载因子k。因此,负载均流误差和谐振均流误差也可以分别用式(15)和式(16)表示。

3 仿真与实验分析

为了进一步验证以上分析均流性能,将无耦合谐振电感IPOP型双谐振LLC变换器与耦合谐振电感IPOP型双谐振LLC变换器的均流特性进行仿真和实验研究,分析这两种变换器的均流误差。双谐振LLC变换器设计参数如表1所示。

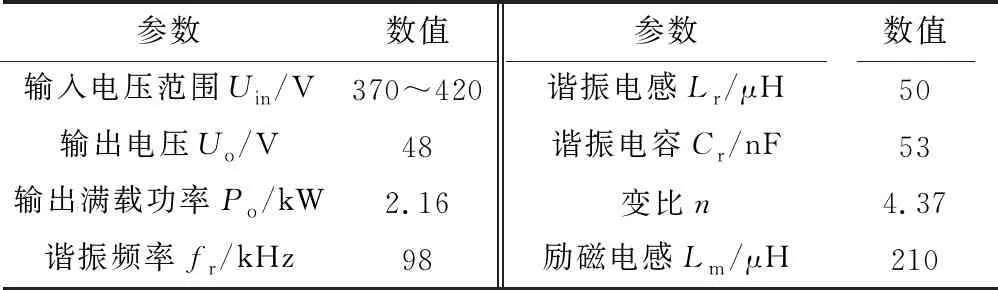
表1 双谐振LLC变换器设计参数

3.1 仿真分析

此处给出无耦合谐振电感IPOP型双谐振LLC变换器与耦合谐振电感IPOP型双谐振LLC变换器的PSIM仿真结果。当Uin为400 V、Uo为48 V,两种变换器在比例系数a=1.1、b=1.1、c=1.1情况下,负载电流Io分别为15 A、25 A、35 A、45 A时,不同负载电流下无耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形分别如图6～图9所示。

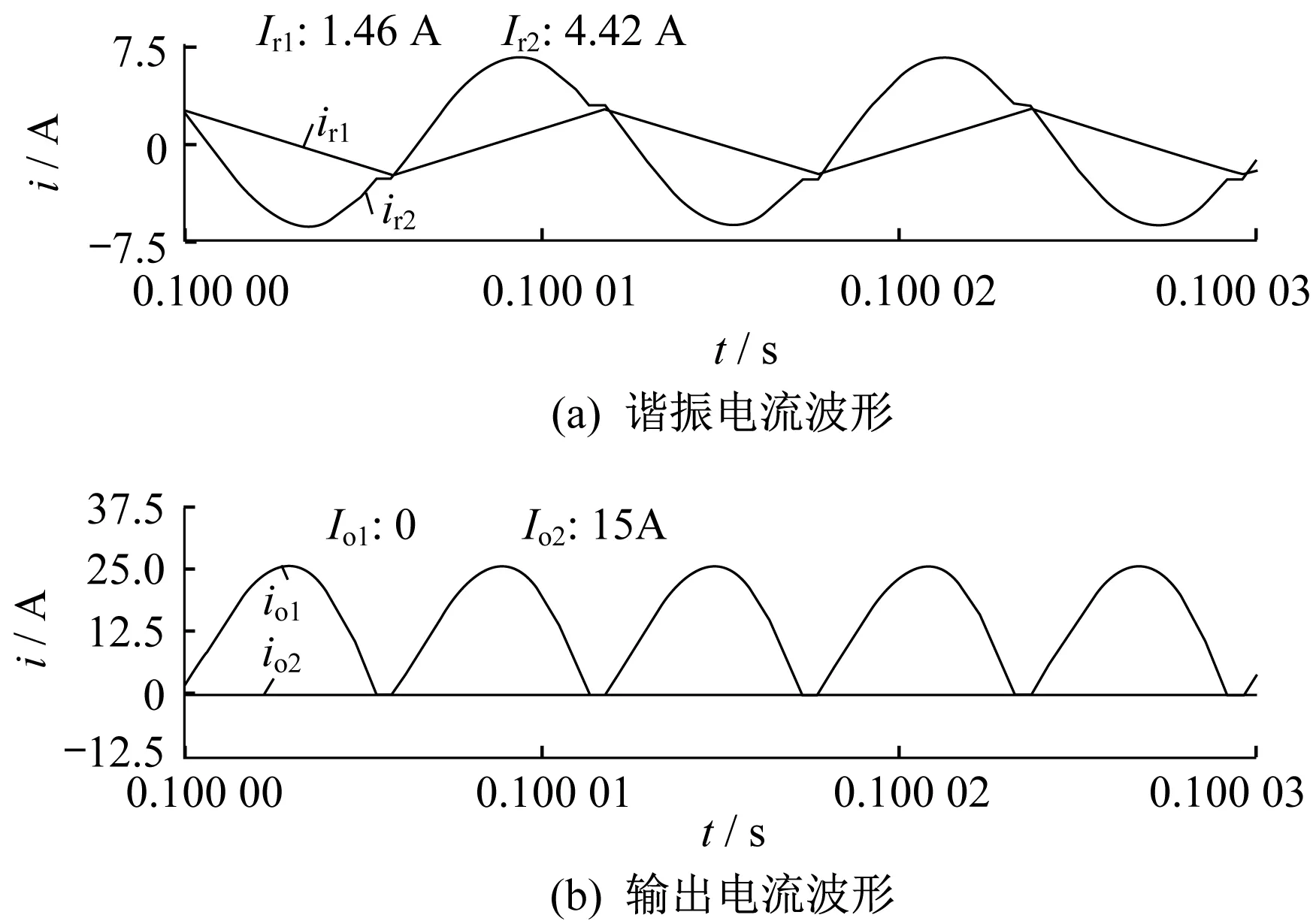
图6 Io为15 A时无耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

图7 Io为25 A时无耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

由图6～图9可知,无耦合谐振电感IPOP型双谐振LLC变换器,在B相的谐振电感、谐振电容、励磁电感参数都存在+10%的偏差于A相时,B相的谐振电流为三角波,其有效值为1.46 A,这是变压器的励磁电感电流。A相的谐振电流有效值随着负载电流的增加而增加。图6～图9中4种情况,A相的输出电流都为整个负载电流,B相的输出电流都为0 A。无耦合谐振电感IPOP型双谐振LLC变换器仿真结果如表2所示。

图8 Io为35 A时无耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

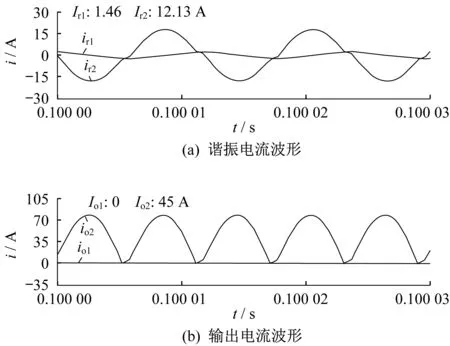
图9 Io为45 A时无耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

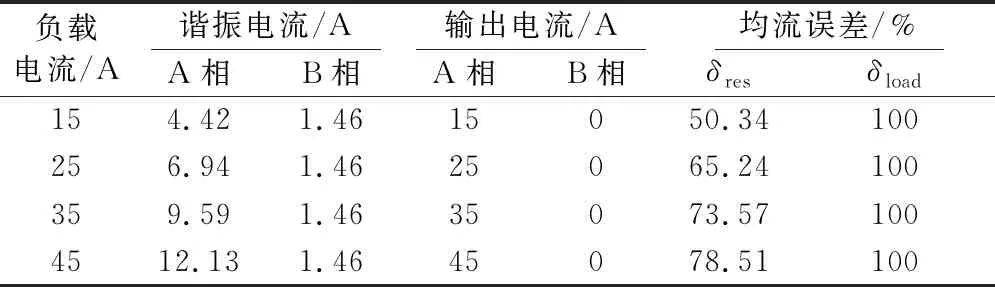
表2 无耦合谐振电感IPOP型双谐振LLC变换器仿真结果

由表2可知,谐振电感未耦合时,当两相谐振元件参数都存在+10%的偏差,两相的输出电流极度不平衡,负载均流误差δload为100%,谐振均流误差δres随负载电流的增大而增大。

耦合谐振电感IPOP型双谐振LLC变换器,在B相的谐振电感、谐振电容、励磁电感参数都存在+10%的偏差于A相时,不同负载电流下耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形如图10～图13所示。由图10～图13可知,A、B相的谐振电流和输出电流都较为接近。耦合谐振电感IPOP型双谐振LLC变换器仿真结果如表3所示。

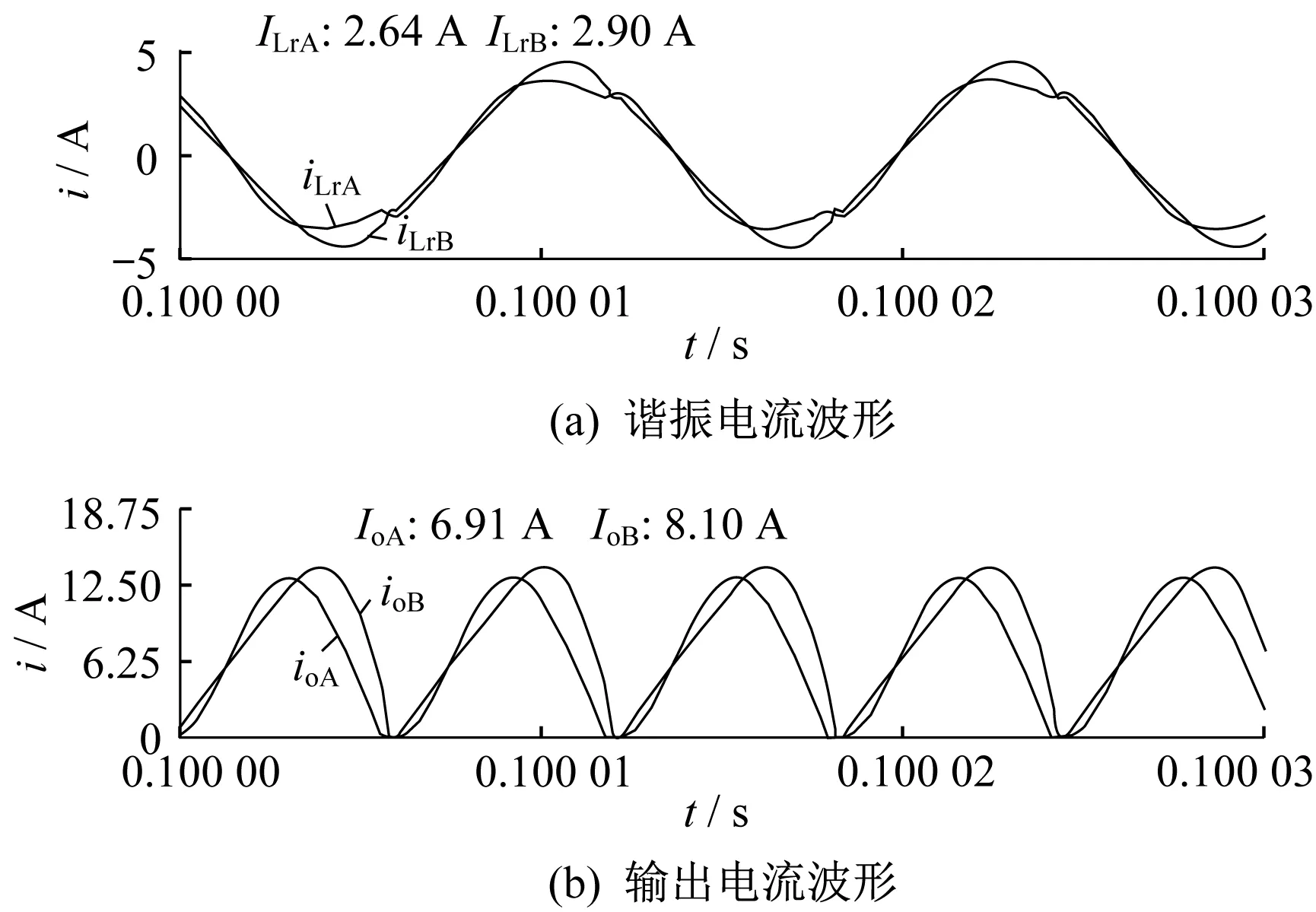
图10 Io为15 A时耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

图11 Io为25 A时耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

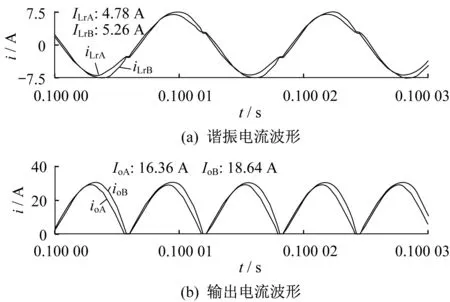
图12 Io为35 A时耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

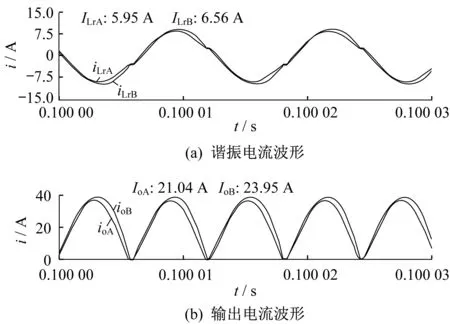
图13 Io为45 A时耦合谐振电感IPOP型双谐振LLC变换器PSIM仿真波形

由表3可知,负载均流误差δload最大值仅为7.93%。此时A、B两相输出电流平均值分别为6.91 A、8.10 A。根据表2和表3分析,谐振电感耦合之后,即使两相谐振元件参数都存在+10%的偏差,两相的均流误差较小,均流特性有明显的改善。

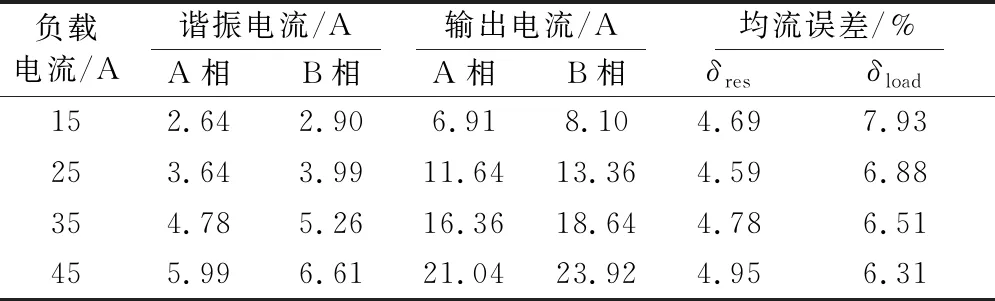
表3 耦合谐振电感IPOP型双谐振LLC变换器仿真结果

3.2 实验分析

为进一步验证理论分析的正确性,同样搭建了两台实验样机进行对比研究。两变换器设计的谐振参数仍按照表1。在实验中,由于二次侧的电流最高达到45 A,PCB布线轨迹应尽可能短,以消除寄生电感的影响。也正因如此,直接测量各相负载电流是不准确的,也不易测量。如上所述,良好的谐振均流效果意味着良好的负载均流效果。因此,实验未对二次侧电流进行测量,而是通过谐振电路的均流误差来评估变换器的均流特性。

在比例系数a=1.1、b=1.1、c=1.1、Uin为400 V、Uo为48 V情况下,负载电流Io分别为15 A、25 A、35 A、45 A时,无耦合谐振电感IPOP型双谐振LLC变换器与耦合谐振电感IPOP型双谐振LLC变换器实验波形分别如图14、图15所示。

由图14可知,B相谐振电流iLrB近似三角波,基本上是变压器的励磁电感电流,这说明B相不提供任何负载电流。实验所得波形与PSIM仿真波形基本一致。图14未给出在负载电流35 A、45 A的波形,这是因为在比例系数a=1.1、b=1.1、c=1.1的极端情况下,A相将承担几乎所有功率,电流应力过大,容易对IPOP型双谐振LLC变换器试验样机造成损坏。

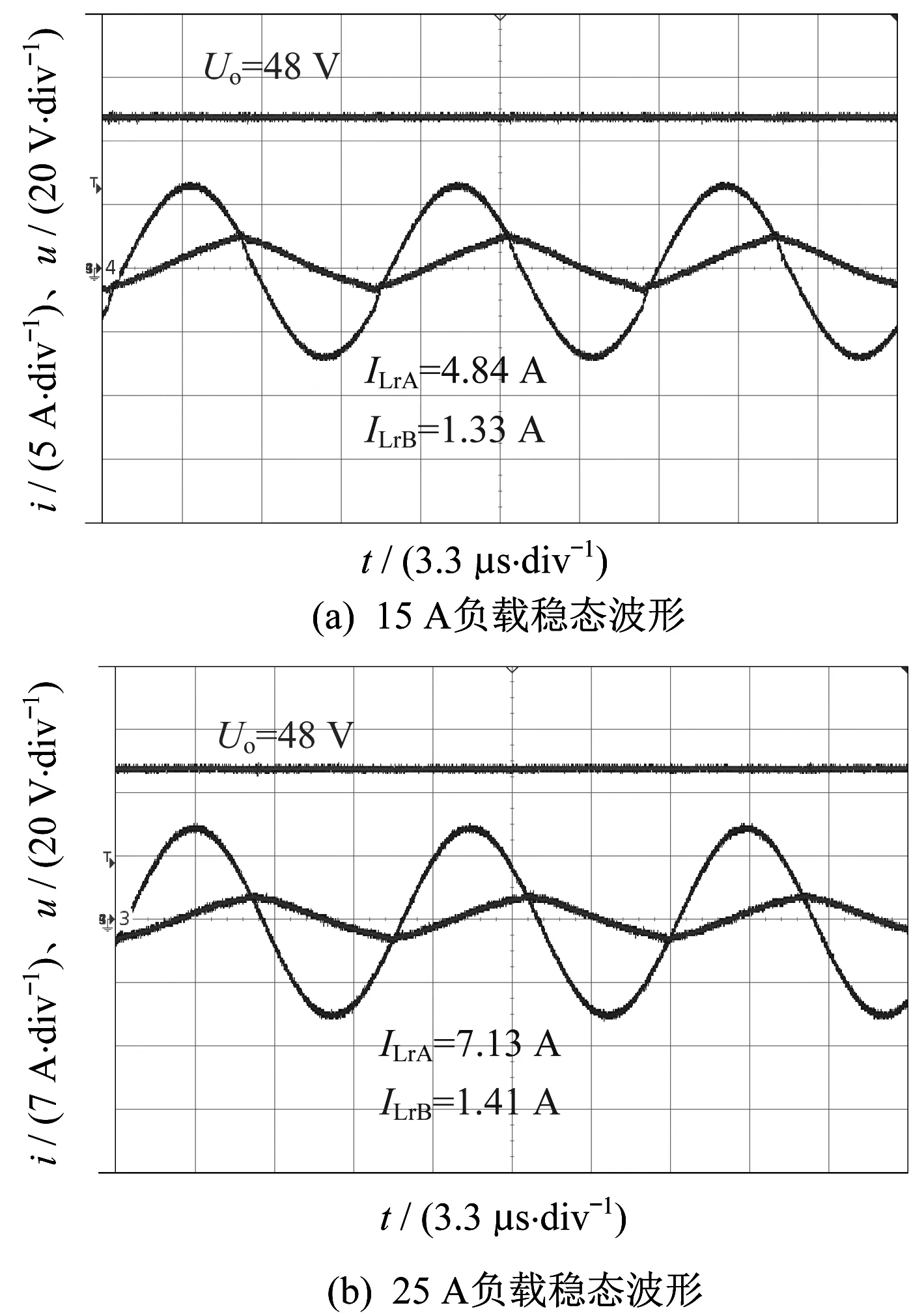
图14 无耦合谐振电感IPOP型双谐振LLC变换器实验波形

由图15可知,A相谐振电流iLrA与B相谐振电流iLrB基本一致,说明两相谐振电路传递几乎相同的功率,且实验所得波形图与PSIM仿真的谐振电流波形基本一致。

无耦合谐振电感IPOP型双谐振LLC变换器与耦合谐振电感IPOP型双谐振LLC变换器在与上述相同情况下,A、B两相谐振电流iLrA、iLrB和谐振均流误差δres在不同负载下的实验结果进行对比。无耦合谐振电感变换器谐振电流与谐振均流误差和耦合谐振电感变换器谐振电流与谐振均流误差分别如图16与图17所示。

由图16可知,随着负载电流的增大,无耦合谐振电感时,A相谐振电流iLrA呈快速增大趋势,意味着该相电路传递的功率也在快速增大;B相谐振电流则基本不变化,意味着该相传递的功率基本不变。谐振均流误差δres同样呈现快速增大的趋势,意味着两相传递的功率差距在不断拉大。

由图17可知,随着负载电流的增大,耦合谐振电感时,A、B两相谐振电流都呈增大趋势,意味着两相谐振电路传递的功率也在不断增大;当负载电流为10 A时,出现谐振均流误差δres实验最大值为5.8%。

由图14、图15的实验波形,图16、图17的谐振电流iLrA、iLrB和谐振均流误差δres的曲线对比可知,耦合谐振电感IPOP型双谐振LLC变换器对均流特性有较好的改善作用。

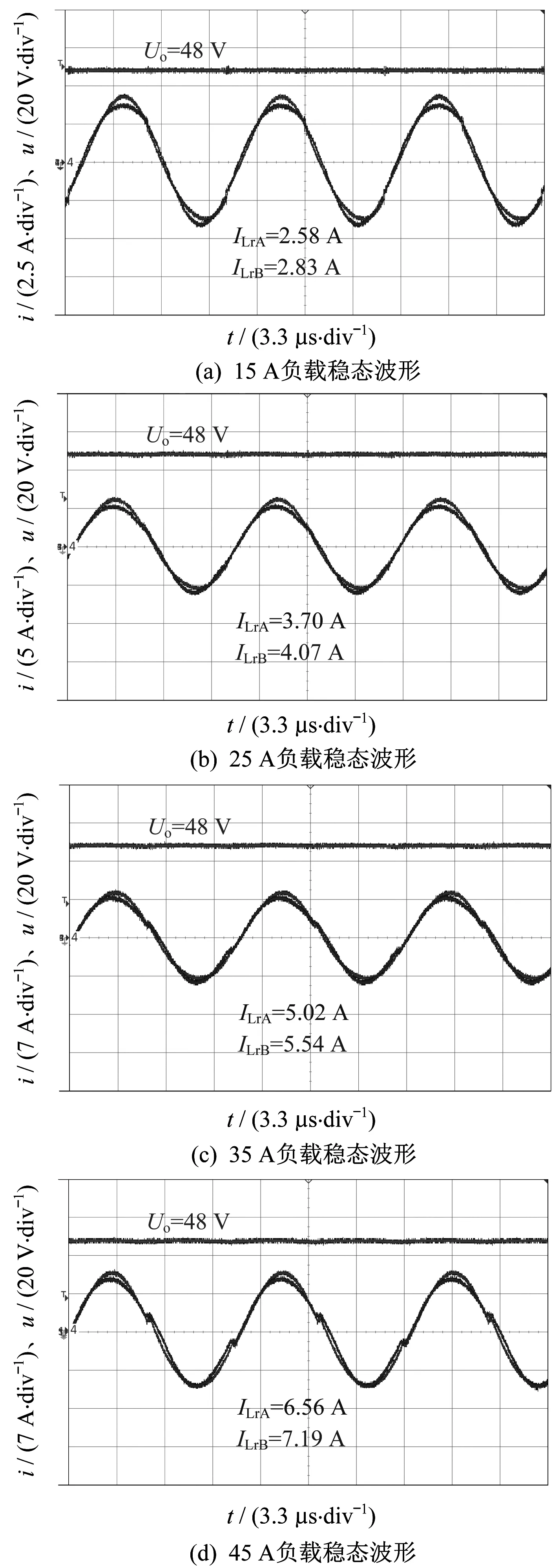
图15 耦合谐振电感IPOP型双谐振LLC变换器实验波形

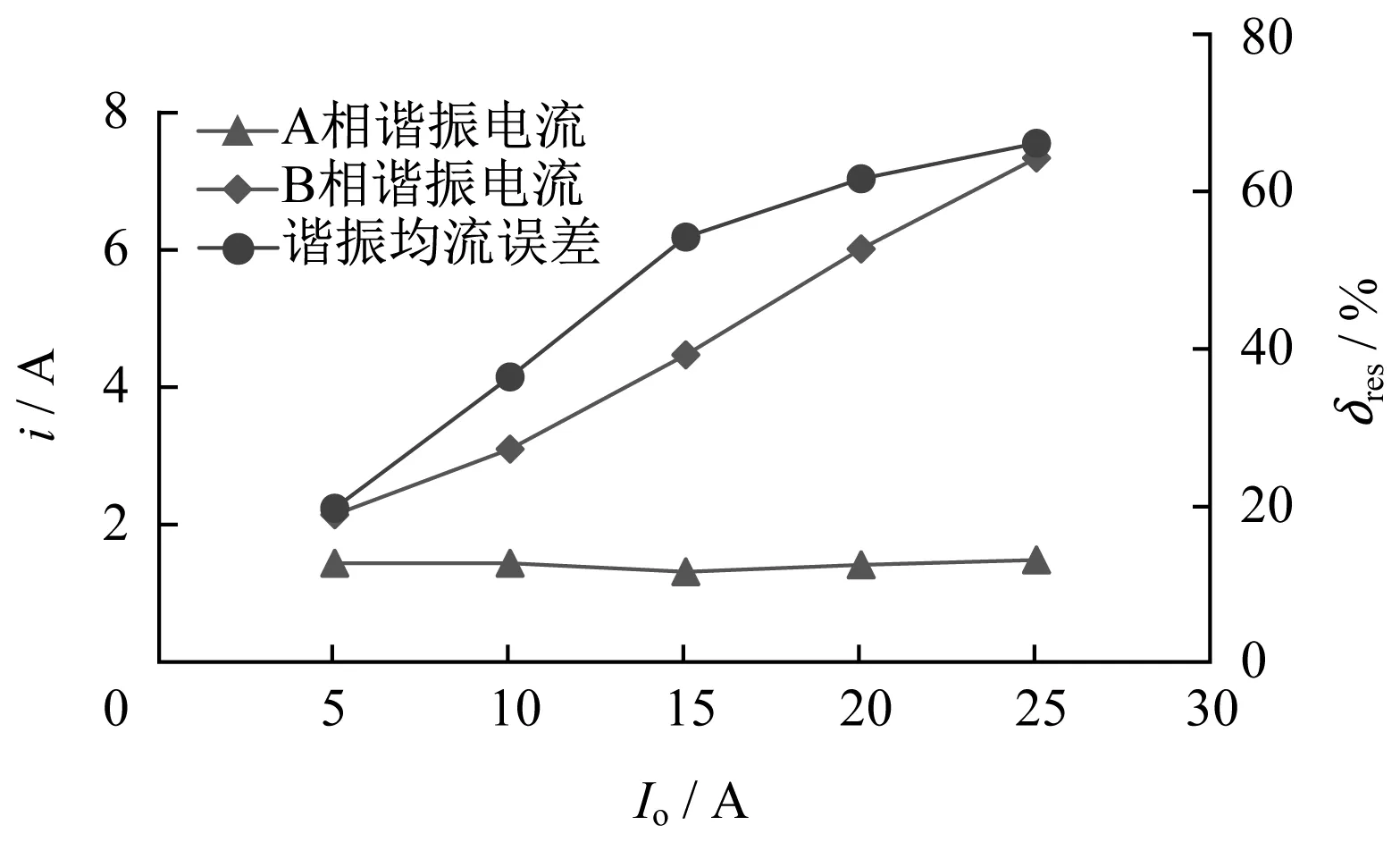
图16 无耦合谐振电感变换器谐振电流与谐振均流误差

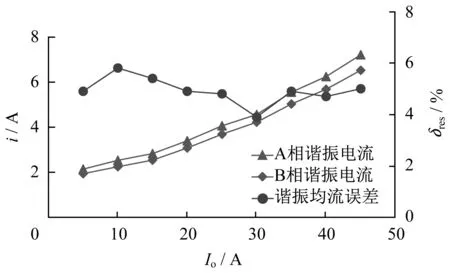
图17 耦合谐振电感变换器谐振电流与谐振均流误差

在输入电压Uin为400 V、输出电压Uo为48 V时,不同负载下,对无耦合谐振电感IPOP型双谐振LLC变换器与耦合谐振电感IPOP型双谐振LLC变换器的效率η进行测试。效率曲线如图18所示。因为无耦合谐振电感IPOP型双谐振LLC变换器存在严重不均流问题,图18中未给出负载电流25 A以上的效率点。耦合谐振电感IPOP型双谐振LLC变换器在负载电流为45 A(满载2.16 kW)时效率最大,为96.32%。

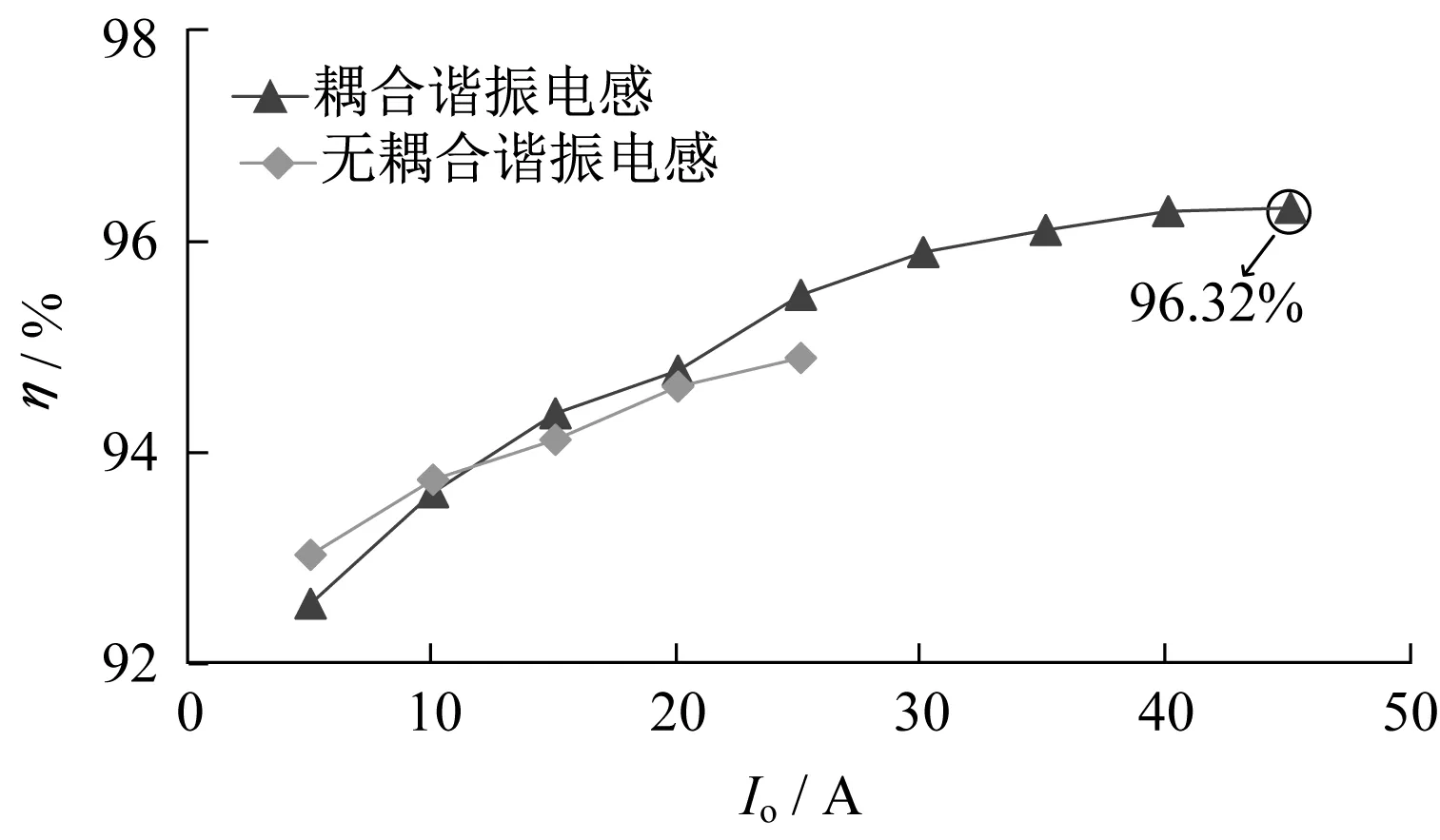
图18 效率曲线

4 结 语

本文提出一种具有自动均流效果的耦合谐振电感IPOP型双谐振LLC变换器,结合基波分析法、PSIM仿真和实验研究得到以下结论:

(1) 所提出的变换器为IPOP结构,不仅实现负载电流均分到两相谐振电路中、减小磁性器件体积、提高功率密度,而且保留了传统双谐振LLC变换器输入电流连续、电流纹波小等优点。

(2) 通过耦合谐振电感的方式,实现自动均流,且无需额外的检测元件及复杂的控制策略。减少了由谐振元件的分散性引起的均流误差源,从而减小无耦合谐振电感IPOP型双谐振LLC变换器的均流误差。谐振电感耦合前和耦合后变换器的仿真和实验对比结果与理论分析结果一致。