具有降压单元的磁集成组合Buck 变换器的研究
荣德生,刘亚迪,孙瑄瑨,吕培贤,任 杰
(辽宁工程技术大学电气与控制工程学院,葫芦岛 125105)
随着信息化技术的迅速发展,计算机、服务器等设备的运算速度和工作频率在成倍地增加,而处理器的工作电压正在进一步降低,如英特尔的桌面处理器i9-9900K 最大睿频可达5.0 GHz,供电电压仅为1.3 V,功率为95 W。近些年来发展很快的区块链技术以及机器学习、深度学习技术都是依托于高运算速率的服务器进行运算和数据处理。故低电压、大功率是未来信息化技术发展的趋势[1-2]。
传统Buck 变换器从理论上来说,电压增益为占空比D,通过调节占空比可任意调节输出电压。然而,当变换器所需电压等级与输入电压相差较大时,变换器必须工作在一个极端的占空比,而极端的占空比会对变换器的瞬态性能造成极大的影响[3],当变换器中的开关管导通时间较短时,在开关频率高的时候,会导致开关管故障,导致变换器的稳定性能下降[4]。为了提高变换器的降压能力,文献[5]在Buck 变换器的基础上对Buck 变换器进行改进,增加了一个二极管和电感,有效降低了变换器的电压增益;文献[6]将文献[5]中改进Buck 变换器中的电感进行磁集成,有效减小了电感电流纹波大小。但文献[5-6]并未给出变换器的提出过程以及对降压结构原理的分析。文献[7]具体分析了二次型Buck 变换器的工作原理,其电压增益与占空比呈平方关系,有效降低了变换器的电压增益。
本文在文献[5-7]的基础上,对Buck 变换器以及Buck-Boost 变换器进行结构变换与重组,提出2种具有降压能力的开关电感单元,分析了其工作实质,提出了降压开关电感与升压开关电容之间的对偶关系。将二次型Buck 变换器中的降压结构进行提取,并与开关电感单元进行组合,提出一种具有组合降压单元的Buck 变换器;将其开关电感模块中的电感进行磁集成,分析了其工作原理,并对变换器磁集成进行了分析,最后通过仿真与实验的方式证明了理论的正确性。
1 降压单元的提出
1.1 2 种开关电感降压单元
1.1.1 开关电感I 型结构
Buck 变换器是一种基本的降压变换器,由于其结构简单,控制方便,被广泛应用于各种降压场合。将Buck 变换器中的电感位置进行变换,得到等效Buck 变换器,如图1 所示。2 种Buck 变换器的工作模式与性能相同,唯一区别就是电感位置不同。
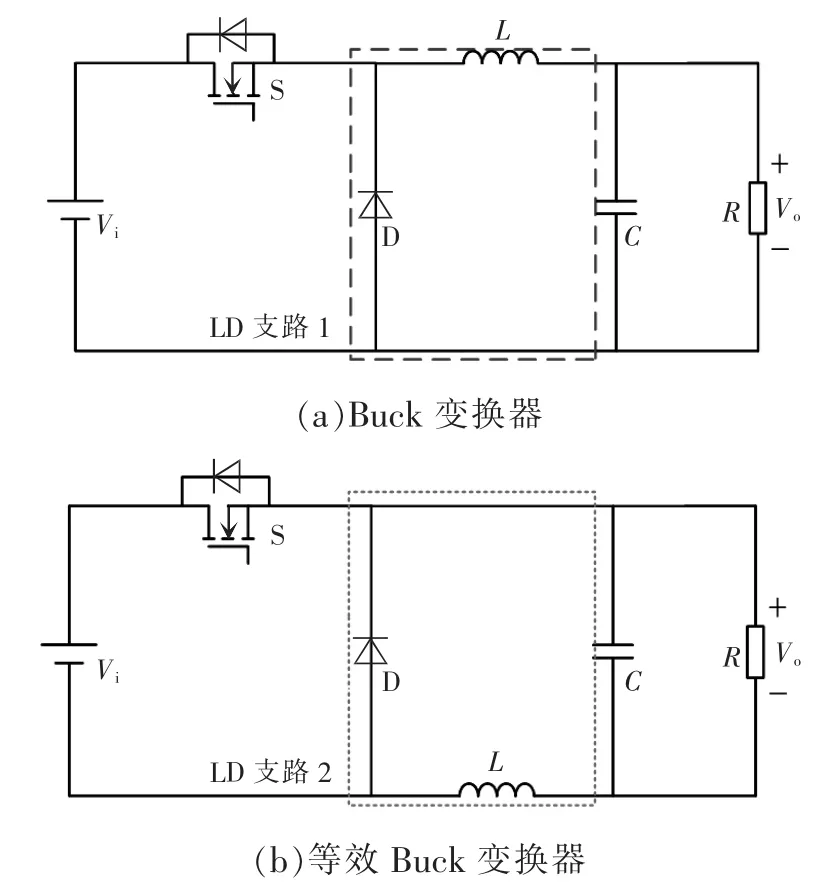
图1 2 种Buck 变换器Fig.1 Two kinds of Buck converter
将图1 中2 种Buck 变换器中的二极管和电感支路(简称LD 支路)进行组合,组合成带有开关电感的Buck 变换器如图2 所示,即为文献[5-6]所分析的变换器结构。
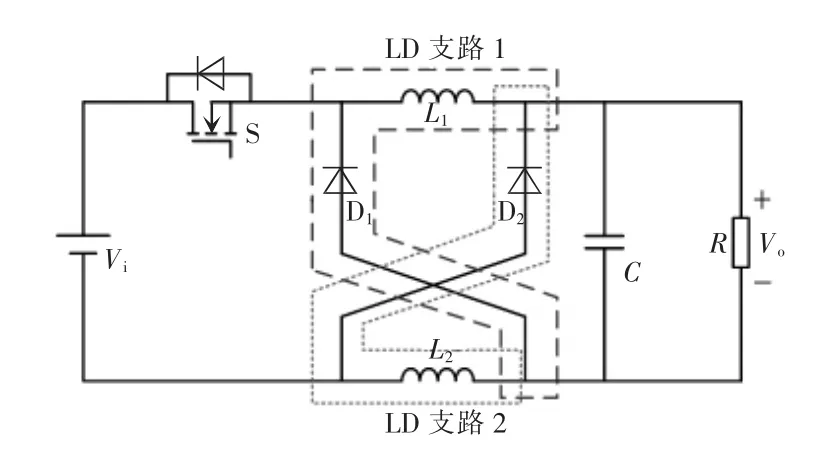
图2 带有开关电感的Buck 变换器Fig.2 Buck converter with switched inductor
带有开关电感的Buck 变换器的电压增益为

与传统Buck 变换器对比,电压增益为原来的1/(2-D),有效降低了变换器的电压增益。
对图2 中的组合LD 网络进行提取,即得降压开关电感I 型结构如图3 所示。在电感储能模态下,二极管D1、D2关断,电感L1与L2串联储能;在电感释放能量的模态下,二极管D1、D2导通,电感L1、L2分别通过二极管D1、D2放电。
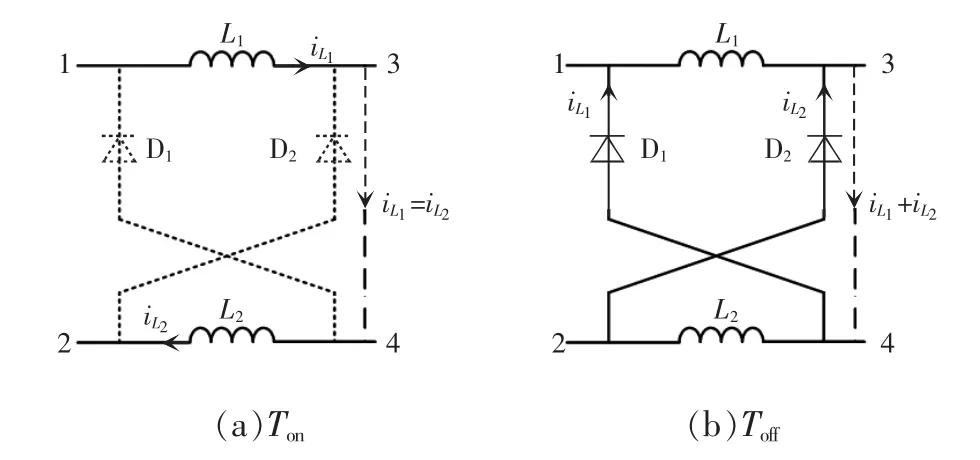
图3 开关电感I 型结构Fig.3 Type-I structure of switched inductor
1.1.2 开关电感Ⅱ型结构
Buck-Boost 变换器是一种输出电压可高于输入电压或者输出电压可低于输入电压的一种单管变换器,与第1.1.1 节Buck 变换器的分析类似,将Buck-Boost 变换器中的二极管的位置进行变换,得到等效Buck-Boost 变换器,2 种变换器如图4 所示。2 种Buck-Boost 变换器的工作模式与性能相同,唯一区别就是电感位置不同。

图4 2 种Buck-Boost 变换器Fig.4 Two kinds of Buck-Boost converter
将图4 中2 种Buck-Boost 变换器中的LD 支路进行组合,组合成带有开关电感的Buck-Boost 变换器,如图5 所示。

图5 带有开关电感的Buck-Boost 变换器Fig.5 Buck-Boost converter with switched inductor
带有开关电感的Buck-Boost 变换器的电压增益为

与传统Buck-Boost 变换器对比,电压增益为原来的1-D/(2-D)倍,变换器的电压增益明显降低。
对图5 中的组合LD 网络进行提取,即得降压开关电感Ⅱ型结构,如图6 所示。与开关电感I 型结构的工作模态相类似,在电感储能模态下,二极管D1、D2关断,电感L1与L2串联储能;在电感释放能量的模态下,二极管D1、D2导通,电感L1、L2分别通过二极管D1、D2放电。
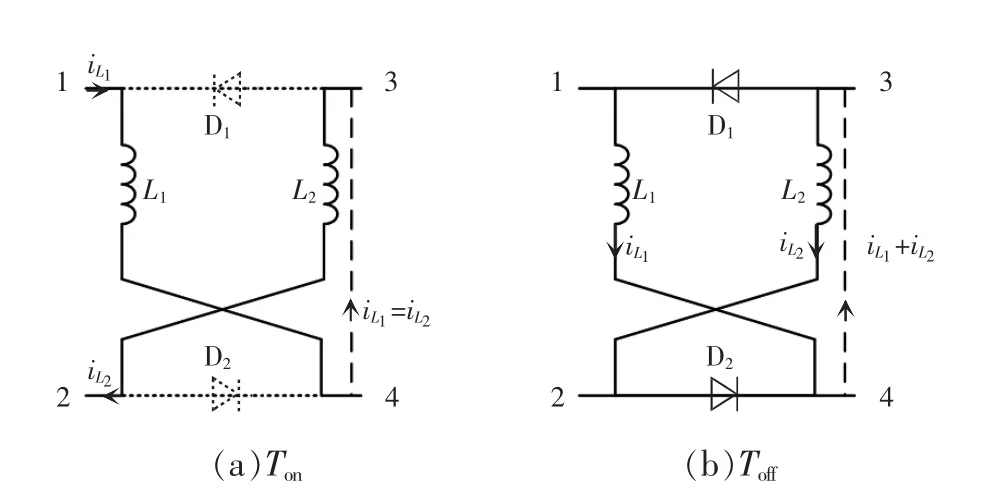
图6 开关电感Ⅱ型结构Fig.6 Type-Ⅱstructure of switched inductor
1.1.3 降压开关电感结构总结
1)降压开关电感的工作实质
根据第1.1.1 节和第1.1.2 节的分析,2 种降压开关电感从结构上来说都是由2 个电感和2 个二极管组成;从工作方式上来说,都是在电感储能模态下2 个二极管均关断,2 个电感并联储能;在电感释放能量的模态下2 个二极管均导通,2 个电感并联向后级释放能量。
开关电感型降压结构的工作实质为:在电感储能模态下,电感“串联”储能;在电感释放能量的模态下,电感“并联”放电。
2)与升压开关电容结构对比
开关电容是一种常见的升压结构[9-13],其由2 个电容和2 个二极管组成,在不增添太多元器件的同时可以使变换器的电压增益成倍提升,广泛应用于各种升压高增益场合。而升压开关电容的工作实质与降压开关电感的工作实质完全相反,在电容充电的模态下,电容“并联”充电;在电容放电的模态下,电容“串联”放电。
根据上述分析,由于降压开关电感结构和升压开关电容结构都是由2 个储能元件(电感或电容)和2 个二极管构成,而对于升压开关电容结构来说,当电容处于储能模态下,二极管导通,两电容通过二极管“并联”充电;当电容处于放电模态下,两二极管截止,两电容串联放电。由于其充放电模态与降压开关电感正好相反,故降压开关电感结构与升压开关电容结构存在对偶关系,如图7 所示。
由图7 可知,降压开关电感结构与升压开关电容结构存在相互之间的对偶关系。以降压开关电感对偶为升压开关电容为例,将开关电感单元中的电感替换为二极管,电感电流方向与二极管导通电流方向一致;将开关电感中的二极管替换为电容,电容的极性与二极管导通电压极性相反。通过以上对偶变换,可将降压开关电感结构转换为升压开关电容结构。反之原理亦然,在此不再赘述。

图7 对偶原则Fig.7 Dual principle
3)降压开关电感结构在其他基本电路的应用
根据第1.1 节的分析,可将开关电感构造思路应用于Cuk、Zeta、Sepic 变换器中如图8 所示,在此不再赘述。
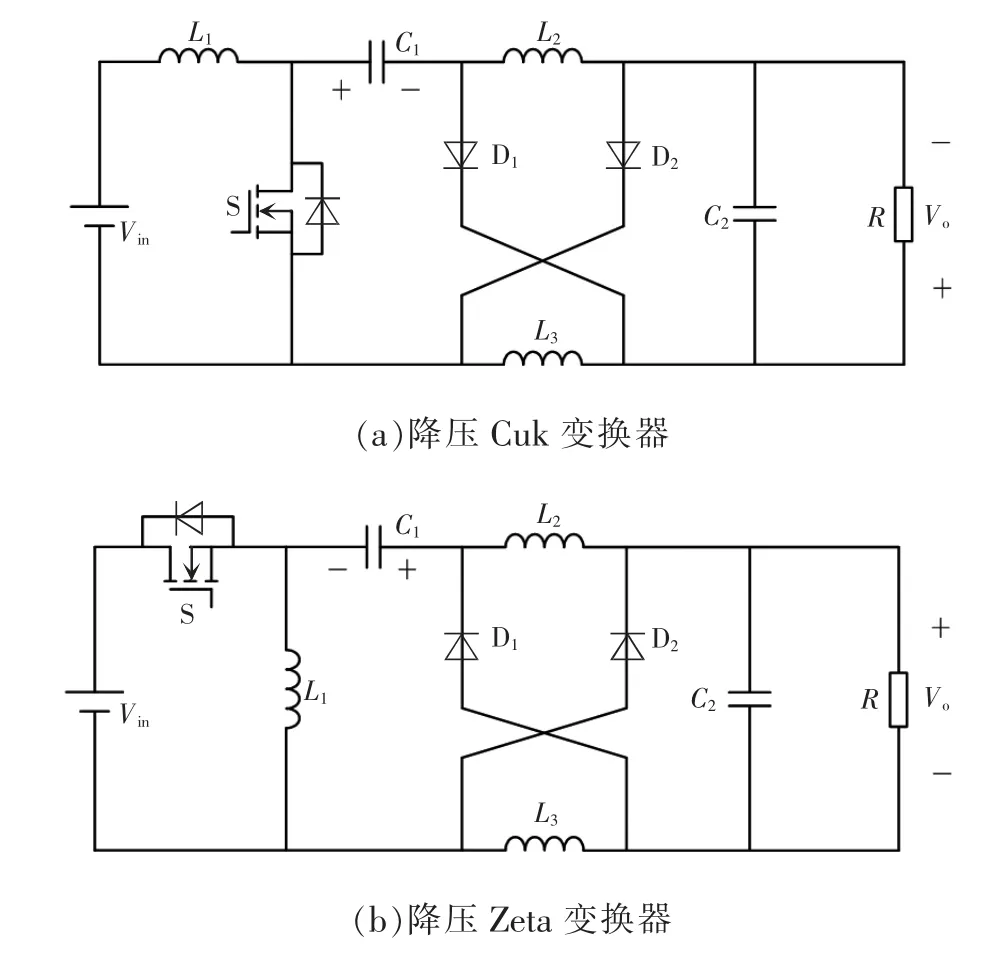

图8 降压开关电感在其他电路中的应用Fig.8 Application of Buck switched inductors in other circuits
1.2 二次型降压结构
二次型Buck 变换器是一种具有较大调压范围的降压变换器,其仅使用1 个开关管即可实现与占空比呈平方关系的电压增益,变换器结构巧妙,在许多降压场合均有应用。根据二次型Buck 变换器的结构[7],提取前级二极管电感电容结构,如图9 所示,该结构可作为降压前级结构。
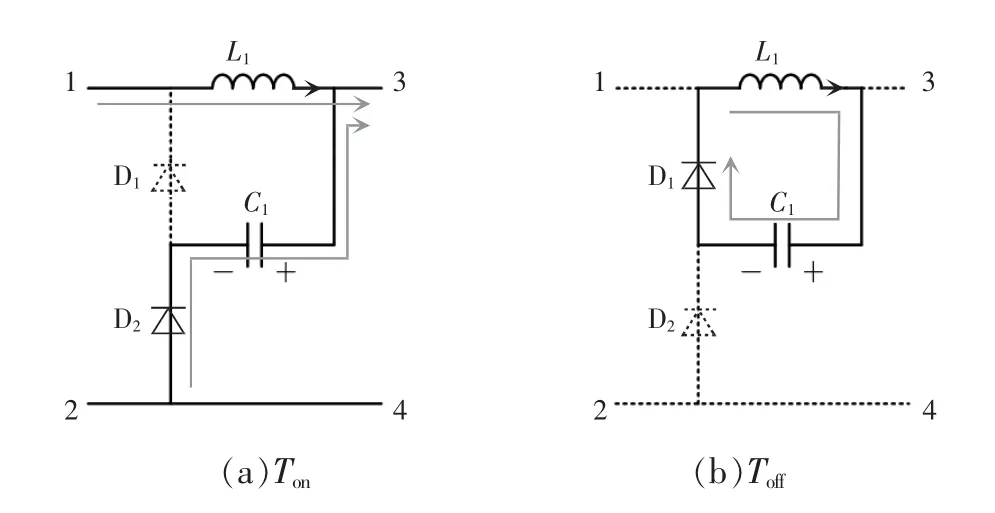
图9 二次型降压结构Fig.9 Quadratic Buck structure
在电感储能模态时,前级电压源(电源或者电容)给电感L1储能,电容C1通过二极管D2向后级释放能量;在电感释放能量模态下,电感L1通过二极管D1给电容C1充电。
2 具有降压单元的磁集成组合降压变换器
2.1 变换器结构提出
将Buck 变换器进行拆分,在开关管前增加二次型降压结构,在后级分别替换降压开关电感I 型结构和开关电感Ⅱ型结构,可得到如下2 种具有组合降压单元的磁集成组合Buck 变换器,如图10 所示。
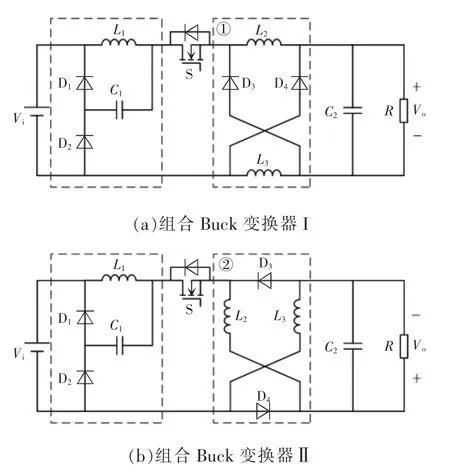
图10 2 种组合Buck 变换器Fig.10 Two kinds of combined Buck converter
根据变换器的工作原理分析,由于后级2 种降压开关电感结构的工作方式均相同,都为串联储能,并联放电,故2 种组合降压变换器从性能上来说是相同的,唯一的区别是组合降压变换器I 的输入电压与输出电压是同向的,而组合降压变换器Ⅱ的输入电压与输出电压是反向的。故本文以组合降压变换器Ⅱ为例,具体分析变换器的各项性能。
2.2 变换器分析
将组合Buck 变换器Ⅱ中的降压开关电感结构中的电感进行集成,得到磁集成组合Buck 变换器,如图11 所示。

图11 磁集成组合Buck 变换器Fig.11 Magnetic integrated combined Buck converter
2.2.1 变换器工作原理
为便于分析变换器的工作原理,做如下3 点假设:①所有开关管、二极管均为理想器件;②电感及电容均为理想器件,忽略寄生效应;③所有电容足够大,其纹波电压可以忽略。令:独立电感L2=L3=L,电感L2与L3的互感为M。
非集成与磁集成具有相同的工作模态,且电压增益在电感电流连续模式CCM(continuous conduction mode)下均不变。变换器在1 个开关周期内共有2 个工作模态,即开关管S 导通模态(模态I)和开关管S 关断模态(模态Ⅱ)。图12 为变换器的2 个工作模态等效电路,图13 为变换器2 种工作模式的主要工作波形。
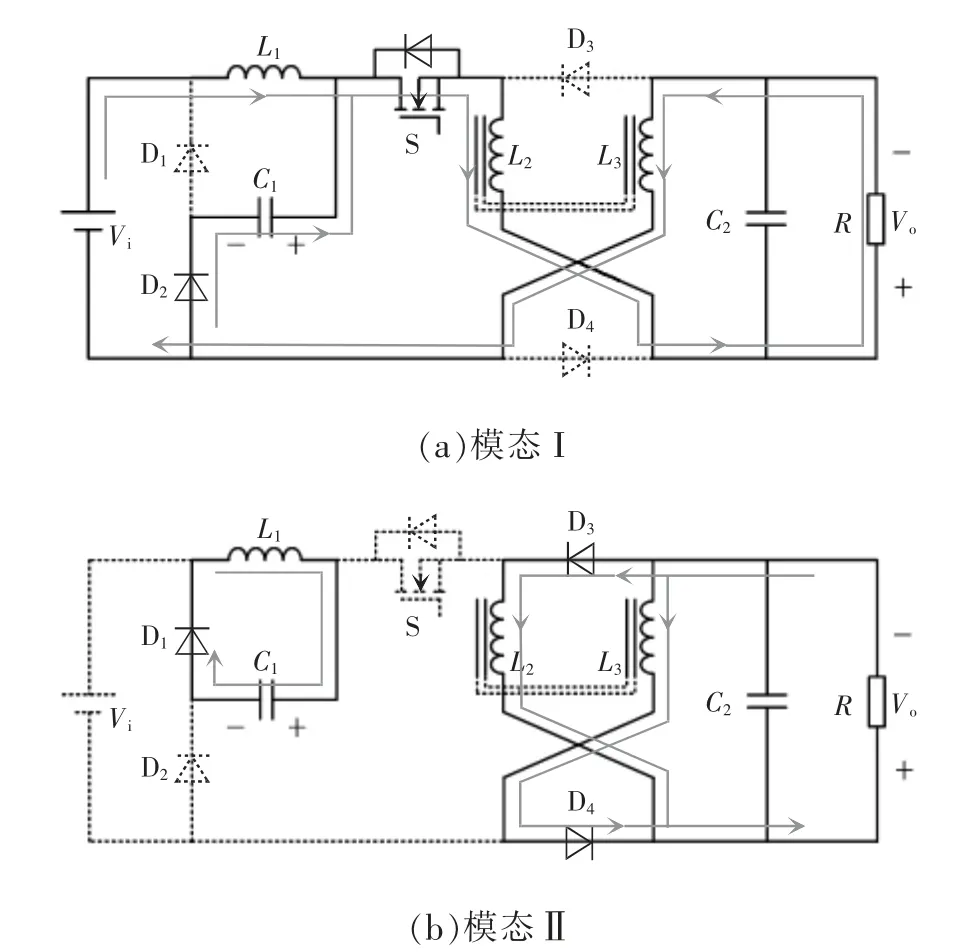
图12 变换器工作模态Fig.12 Operating modes of converter
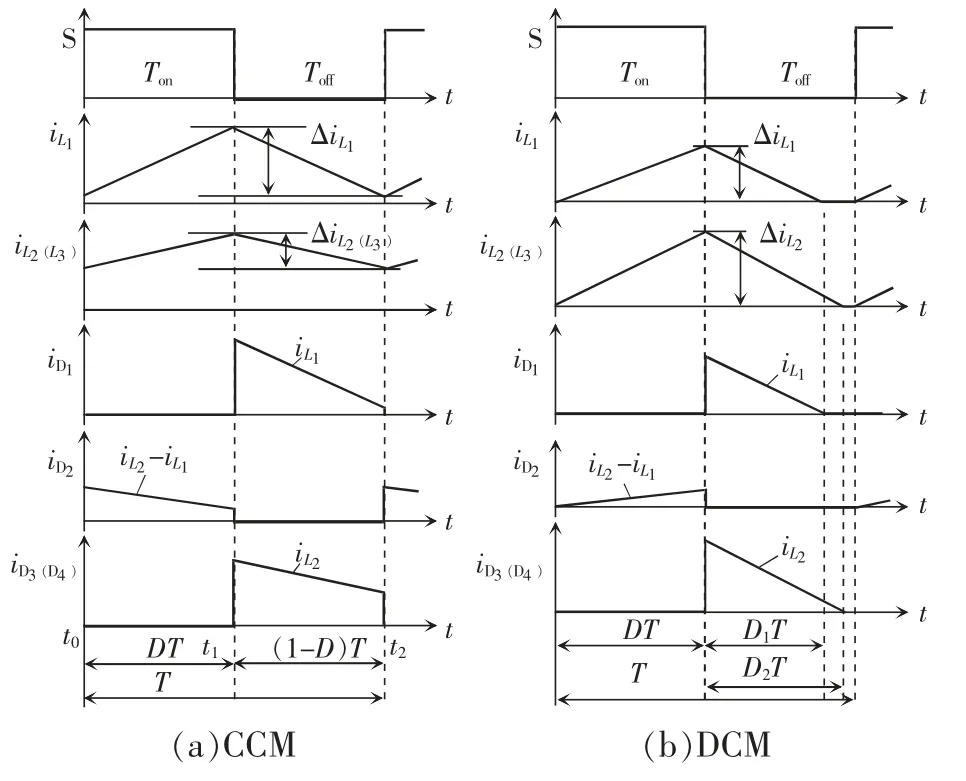
图13 变换器主要波形Fig.13 Main waveforms of converter
工作模态1[t0,t1]:开关管S 开通,二极管D2导通,D3、D4截止,电源给电感L1储能,电源和电容C1给电感L2、L3串联储能,电感电流增加,在此模态下,有

工作模态2[t1,t2]:开关管S 关断,二极管D1、D3、D4导通,D2截止,电感L1通过D1给电容C1充电,电感电流减小;电感L2通过D3与电感L3通过D4并联给负载供电,电感电流、减小;在此模态有
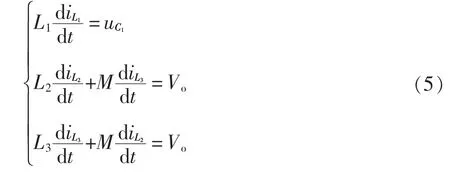
由于电感L2=L3=L 且两电感并联向负载放电,故也有=代入式(5),得
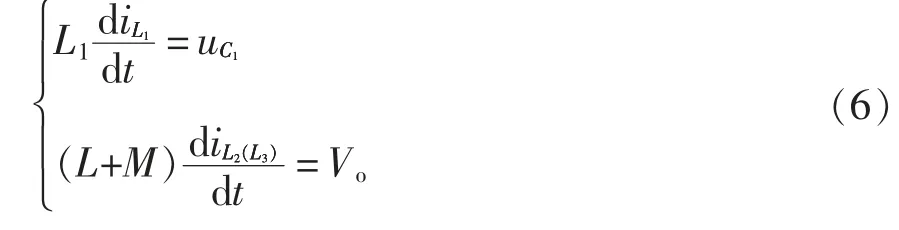
2.2.2 变换器性能分析
1)CCM 模式下电压增益
由式(4)和式(6)可得各电感电流在增加和减小时的变化量表达式。当变换器工作在连续工作模式(CCM)下时,电感电流在增加量和减小量分别为

由式(7)和式(8),根据电感在1 个周期内电压伏秒积面积平衡原理,得
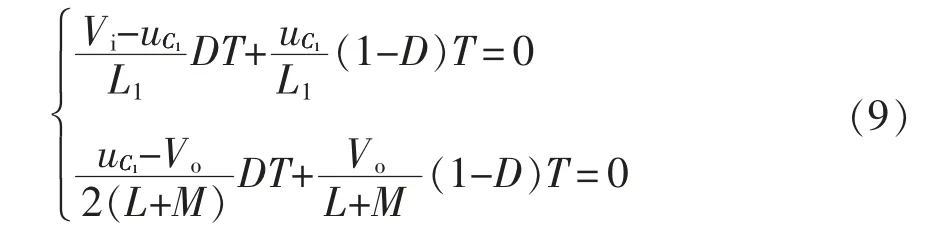
由式(9)可得变换器得电压增益为

由式(10)可知,Vo与Vi方向相反,对比传统二次型Buck 电路,电压增益减小到其的1/(2-D),电压增益进一步降低,具有电路更宽的电压调节范围,避免变换器工作在极限占空比情况。
2)DCM 模式下电压增益
当变换器工作在断续工作模式DCM(discontinuous conduction mode)下时,变换器主要波形如图13(b)所示。
变换器工作在DCM 模式下共存在3 种情况:一种为电感L1电流断续,L2、L3连续;一种为电感L1电流连续,L2、L3断续;另一种为电感L1、L2、L3均断续;图14 为两电感均断续的情况。假设D1T 为电感L1的电流下降时间,D2T 为电感L2、L3的电流下降时间,其工作分析方式与模式CCM 下类似,不再赘述分析,仅给出DCM 模式下的电压增益表达式,即

式中,K1、K2为变换器的无量纲参数。
将D1=1-D;D2=1-D 代入式(12)和式(13),得到在L1与L2、L3不耦合情况下的临界电感L1c、L2(3)c,即
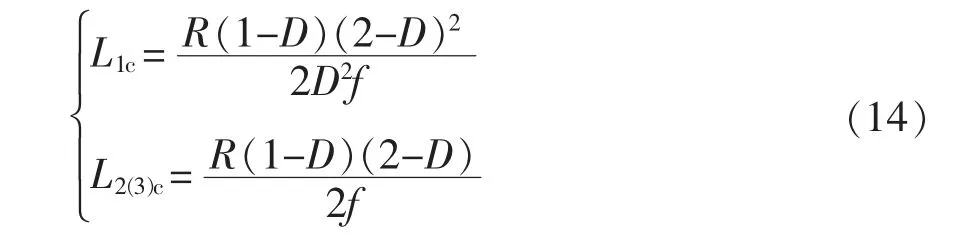
所以,当L1>L1c、L2>L2c时,电感L1、L2、L3的电流连续,变换器工作在CCM 下。
3)电压应力分析
在选择合适的器件的时候,电压应力是选择器件的重要依据,变换器在CCM 下各器件的电压应力分别如下。
各电容电压应力为

开关管电压应力为

各二极管电压应力为
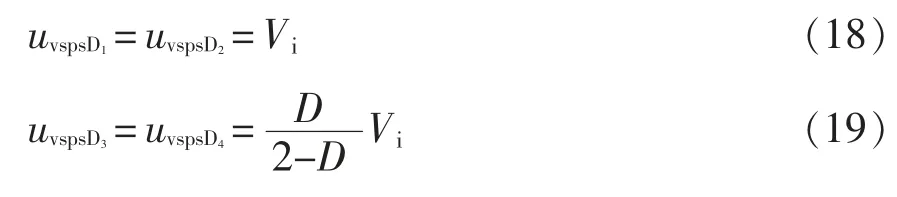
4)不同变换器对比
将具有组合降压单元磁集成组合降压变换器与传统Buck 变换器、Buck-Boost 变换器、带有开关电感的Buck 变换器、带有开关电感的Buck-Boost变换器以及二次型Buck 变换器进行对比,如表1所示。
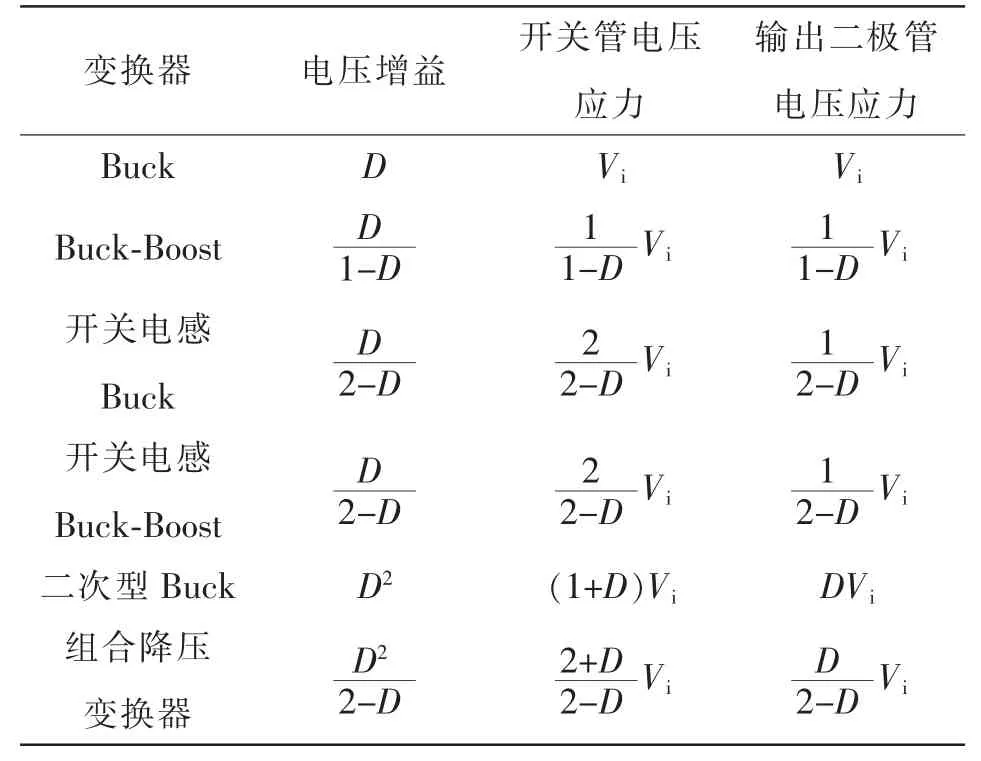
表1 不同变换器对比Tab.1 Comparison among different converters
由表可知,组合降压变压器具有最低的电压增益,电压调节范围最宽;而开关电感Buck 变换器和开关电感Buck-Boost 变换器相较于Buck 变换器和Buck-Boost 变换器来说,电压增益也得到了明显的降低。而根据开关管的电压应力对比可发现,组合降压变压器虽电压应力要略高于Buck 变换器和开关电感Buck 变换器,但相较于Buck-Boost 变换器来说,电压应力还是有一定优势的。而对比输出二极管的电压应力,组合降压变压器的输出二级管相比其他变换器,具有最低的电压应力。开关电感Buck 和二次型Buck 的输出二级管电压应力也不高。
2.2.3 电感电流纹波分析
由式(7)和式(8)可知,在变换器输入电压确定的情况下,电感L1的电流纹波只与电感L1有关,而电感L2、L3的电流纹波不仅与自感量有关,还与他们之间的互感量有关。假设电感L2与L3的耦合系数为k,则有

将条件L2=L3=L 与式(20)代入式(7)和式(8),则在电感电流上升阶段有
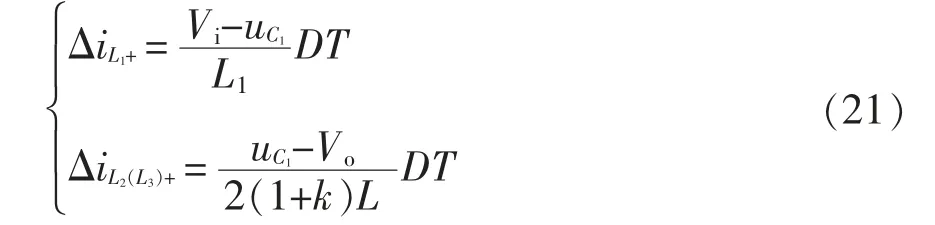
在电流上升阶段电感L2(L3)电流为

根据图14 以及式(22)可知,当电感集成以后,耦合电感中的电流纹波为未集成时独立电感纹波的1/(1+k)。当k 趋近于1 时,即两电感处于全耦合情况,电感电流纹波减小最多,为未集成时独立电感纹波的1/2,故在设计耦合电感器的时候,应使电感L2与L3正向全耦合。

图14 ε 与k 的关系曲线Fig.14 Curve of ε vs k
3 集成磁件设计
根据第2.2.3 节中的电感电流纹波分析可知,当开关电感中2 个电感完全正向耦合时,电感电流纹波的减小倍数最大,电感电流纹波最小,故需设计正向全耦合电感。
为了减小电感线圈的漏感和避免磁芯饱和,在设计磁芯的时候需考虑以下因素[14]:①变换器的工作频率,进而选择合适的磁芯材料;②在缠绕线圈的时候要紧密均匀分布;③在满足耐压值的前提下减少绝缘层;④通过合理的缠绕方式和选择合适的磁芯形状尽量减小磁件的漏感。
由于铁氧体的电阻率比单质金属或合金磁性材料大得多,而且还有较高的介电性能,故选择铁氧体作为磁芯材料;由于ETD 磁芯中柱为圆形,故绕制接线方便,与相同截面的长方体相比,单匝的绕组的长度缩短,且漏感较小,故磁芯结构选择ETD 结构。由于两电感参数相同,电感感值相等,为了减小漏感,将两电感以双线并绕的方式缠绕在ETD 磁芯的中柱上,如图15 所示。为了避免磁芯饱和,需要开有一定的气隙。

图15 耦合电感示意Fig.15 Schematic of coupled inductor
4 实验验证
为了验证磁集成组合降压变换器分析的正确性,在实验室的基础上,设计并制作了一台实验样机,样机参数如下:输入电压Vi=48 V,输出电压Vo=12 V,开关频率f=50 kHz,独立电感L1=80 μF,耦合电感L1=L2=20 μF,电容C1=47 μF,电容C2=100 μF,负载R=5 Ω。开关管选择型号为IRF540N,二极管选用肖特基二极管MBR20100,电流采用ETA5301A电流探测钳进行测量,单位为100 mV/A。独立电感器L1使用铁硅铝环形磁芯,耦合电感使用ETD32,采用双线并绕方式进行缠绕,实测电感参数如表2所示。

表2 电感实测值Tab.2 Measurement values of inductance
耦合电感与实验样机平台如图16 所示,变换器主要波形如图17 所示。

图16 实验样机平台Fig.16 Experimental prototype platform
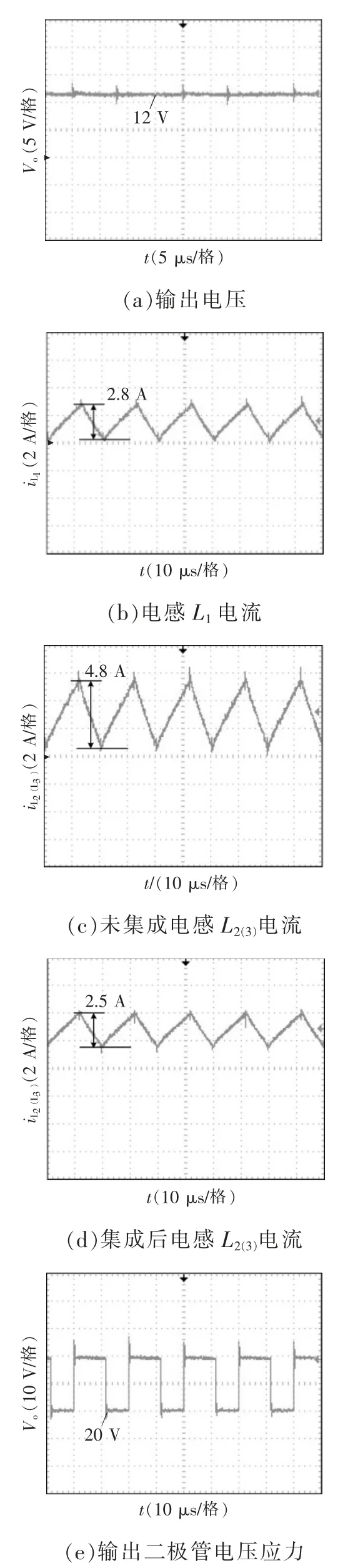
图17 变换器主要波形Fig.17 Main waveforms of converter
根据实验实测波形,磁集成前后的输出电压均约为12 V,与理论分析相符。磁集成前,独立电感电流纹波约为4.8 A;磁集成后,耦合电感电流纹波下降至2.8 A,约为未集成时的58.3%,由于漏感的存在其误差在可接受的范围内。由于耦合前后输出二极管电压应力不变,故只测量耦合后的电压应力,约为20 V,理论与实际相符合。
在保持输出电压恒定12 V 情况下,改变功率负载大小,得到实验样机参考效率曲线如图18 所示。调节负载的大小,变换器的输出功率在20~120 W 之间变化时,样机效率不断增加而趋于平稳,随着输出功率的增大,样机效率最高约为94.8%。

图18 样机效率曲线Fig.18 Efficiency curve of prototype
5 结论
本文通过分析传统Buck 变换器、Buck-Boost变换器以及等效变换组合的方式,给出了2 种降压开关电感结构;通过对降压开关电感的工作实质进行了分析,得到“串联充电、并联放电”的降压实质与“并联充电、串联放电”的升压实质,给出了降压开关电感结构与升压开关电容结构的对偶关系。将二次型Buck 变换器的降压结构进行了提取,并与2 种降压开关进行重新组合,提出了具有降压单元的磁集成组合Buck 变换器,通过理论和实验分析,降压结构与所提变换器具有以下特点:
(1)本文3 种降压单元均可灵活应用于各种降压场合,也可组合形成新型降压变换器。
(2)具有降压单元的组合Buck 变换器电压增益为其D/(2-D),提升了变换器的降压能力,避免变换器工作在极限占空比的情况。
(3)磁集成后,耦合电感电流纹波减小,是独立电感电流纹波的一半。

