新型高增益耦合电感组合Sepic 变换器
荣德生,黄 鹤,孙瑄瑨
(辽宁工程技术大学电气与控制工程学院,葫芦岛 125105)
太阳能、风能等新型能源,具备可再生、无污染的特点,近年来发展迅速,应用日益普及。新能源核心组件输出电压较低,为给后级逆变装置或者直流电网提供足够电压,需增加DC-DC 变换器进行升压。DC-DC 变换器作为其核心单元备受关注,而高增益、高效率的DC-DC 变换器已经成为研究热点。
为了提升传统Boost 变换器的电压增益,近年来,学者们提出了各种解决方案,包括级联变换器、倍压单元倍压、耦合电感倍压和隔离式变换器等[1-4]。其中采用耦合电感结构、设置合理的匝比、可灵活调节变换器的电压增益,成为提升变换器电压增益行之有效的方案。文献[5]提出了带耦合电感Boost 变换器,调节变换器匝比,即可有效调节变换器电压增益,但由于漏感的存在,导致漏感与开关器件寄生电容会产生谐振,开关管关断瞬间,会产生较大的电压应力;文献[6-7]在基本耦合电感Boost 变换器的基础上,通过增添无源和有源箝位电路,吸收漏感能量,提出了一系列具有箝位电路的高增益耦合电感Boost 变换器;文献[8-10]将耦合电感与电容在前级组合,通过耦合电感副边给倍压电容储能,在放电状态下一同串联放电,该方案既抑制了电容储能时过大的电流冲击,又大大提升了电压增益;文献[11-13]详细总结了各种具有耦合电感的高增益Boost 变换器的结构;文献[14]通过将二次型Boost变换器中的电感替换为耦合电感,提出了双耦合电感二次型Boost 变换器;文献[15-17]提出了耦合电感与倍压电容组合的一系列高增益变换器,其电容-二极管支路既作为电容倍压支路,又作为箝位吸收回路。
本文受文献[15-17]的启发,在基本Sepic 变换器的基础上,引入耦合电感结构并与二极管-电容倍压单元DCM(diode-capacitor multiplier)进行组合,提出一种新型高增益耦合电感组合Sepic 变换器。通过调节耦合电感匝比N,灵活调节变换器的电压增益。该变换器保留了Sepic 变换器输入电流连续的特性,且利用Sepic 结构中的电容-二极管支路作为箝位吸收支路,吸收漏感能量,可有效减小由电容引入带来的电流冲击,并减小了开关管的电压应力。
1 高增益耦合电感组合Sepic 变换器的提出
首先将传统Sepic 变换器的结构作为基底,将DCM 单元与Sepic 变换器结构进行组合,提升Sepic变换器的电压增益,同时将Sepic 变换器中的前级电感替换为耦合电感的原边,副边与DCM 单元中的电容进行串联组合成为耦合电感电容倍压支路,得到高增益耦合电感组合Sepic 变换器,其拓扑如图1 所示。
由图1 可知,耦合电感原边与电容C1和C3、二极管D1以及电感L1组成Sepic 基底,二极管D1与电容C3不仅作为Sepic 基底的一部分,同时也作为箝位吸收支路,吸收耦合电感的漏感能量。耦合电感副边与电容C2以及二极管D2组成耦合电感电容倍压支路。由于耦合电感的存在,使得Sepic 变换器的电压增益进一步提升,通过调节耦合电感匝比,可以调节变换器的电压增益。

图1 高增益耦合电感组合Sepic 变换器拓扑Fig.1 Topology of high-gain coupled inductor combination Sepic converter
2 工作原理分析
2.1 变换器等效电路
高增益耦合电感Sepic 变换器的等效电路如图2 所示。由图2 可知,耦合电感是由其漏感Lk、励磁电感Lm以及耦合电感的匝比为N=n2/n1的理想变压器组成的。
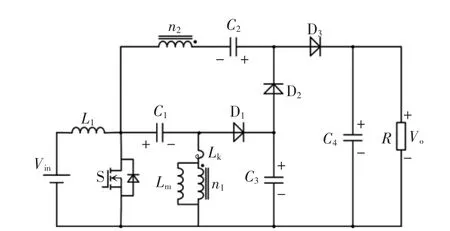
图2 高增益耦合电感组合Sepic 变换器等效电路Fig.2 Equivalent circuit of high-gain coupled inductor combination Sepic converter
为了便于分析变换器的工作原理,假设:
(1)设开关管、二极管均为理想器件,即导通关断时间均为0,且关断电阻无限大,导通压降为0;
(2)电感及电容均为理想器件,忽略寄生效应;
(3)所有电容足够大,其纹波电压可以忽略;
(4)耦合电感的耦合系数k=Lm/(Lm+Lk)。
2.2 变换器模态分析
假设励磁电感Lm与电感L1的电流均连续,即工作在连续导电模式CCM(continuous conduction mode)下,在一个开关周期内,变换器共存在5 种工作模态:模态Ⅰ~模态Ⅴ。各工作模态的等效电路如图3 所示[18-20]。高增益耦合电感组合Sepic 变换器的主要波形如图4 所示。
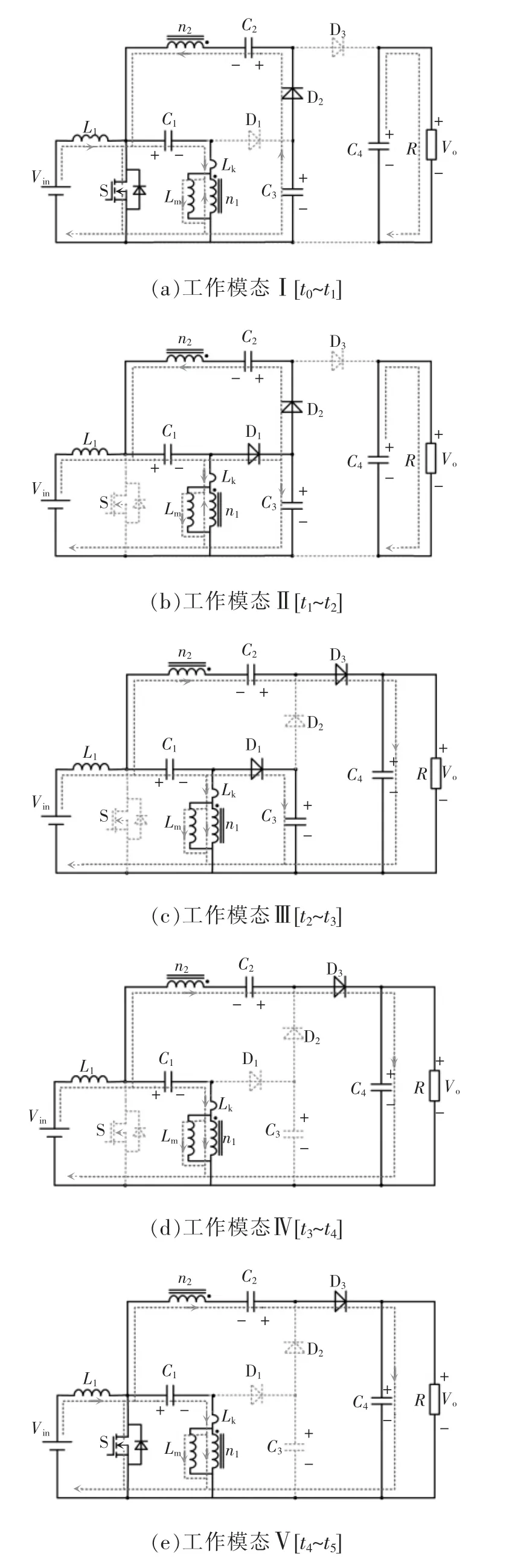
图3 耦合电感组合Sepic 变换器各工作模态的等效电路Fig.3 Equivalent circuit of coupled inductor combination Sepic converter in each working mode

图4 高增益耦合电感组合Sepic 变换器的主要波形Fig.4 Main waveforms of high-gain coupled inductor combination Sepic converter
1)模态I[t0~t1]
在工作模态I[t0~t1]下,开关管S 导通,二极管D1、D3关断,二极管D2导通;输入电压Vin加在电感L1的两端,电感L1充电储能,电感L1的电流线性上升;同时输入电压Vin为电容C1及耦合电感原边充电,励磁电感Lm充电储能;耦合电感副边及电容C3开始给电容C2充电,二极管D2中的电流从0 开始上升,实现零电流开通。在此模态下,励磁电感电流和漏感电流分别为

2)模态Ⅱ[t1~t2]
在工作模态Ⅱ[t1~t2]下,在t1时刻,开关管S 关断,二极管D1、D2导通,二极管D3关断;电感L1及输入电源Vin向电容C1充电,并通过二极管D1给C3充电,电感L1的电流线性下降;耦合电感漏感Lk的能量经过二极管D1被电容C3吸收,漏感电流快速下降;同时副边绕组通过D2继续向电容C2充电。至t2时刻,副边绕组电流下降至0,二极管D2实现零电流关断,此模态时间较短。电容C1、C2、C3两端电压分别为、、。则励磁电感电流和漏感电流分别表示为
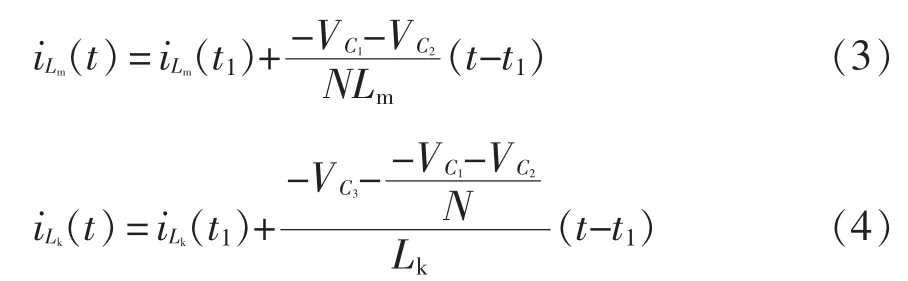
3)模态Ⅲ[t2~t3]
在工作模态Ⅲ[t2~t3]下,开关管S 关断,二极管D1、D3导通,二极管D2关断;电感L1依旧处于放电状态,电感L1的电流持续下降;耦合电感漏感Lk的能量经过二极管D1向电容C3转移,漏感电流下降;同时耦合电感副边和电容C2通过二极管D3一同为负载供电,同时为电容C4充电;在t3时刻,漏感Lk的能量已经释放完毕,二极管D1中的电流下降到0,二极管D1实现零电流关断。在此模态下,励磁电感电流和漏感电流分别为
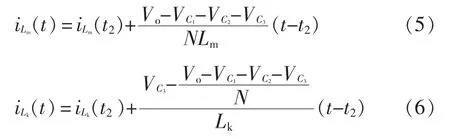
4)模态Ⅳ[t3~t4]
在工作模态Ⅳ[t3~t4]下,开关管S 关断,二极管D1、D2关断,二极管D3导通;输入电源Vin与电感L1为电容C1及耦合电感原边充电,励磁电感Lm充电储能;电感L1依旧处于放电状态;同时耦合电感副边及电容C2一同为负载供电,同时给电容C4充电,漏感Lk的能量已经释放完毕。在此模态下,励磁电感电流和漏感电流分别为
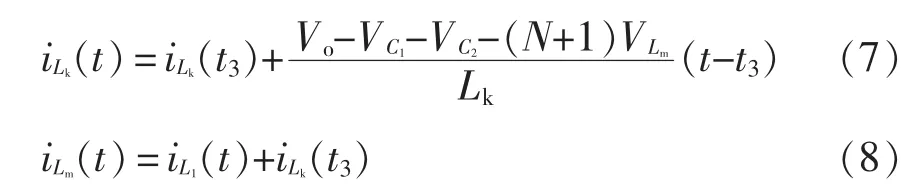
5)模态Ⅴ[t4~t5]
在工作模态Ⅴ[t4~t5]下,开关管S 导通,二极管D1、D2关断,二极管D3导通;输入电源Vin加在电感L1的两端,电感L1充电储能,电感L1的电流线性上升;同时输入电源Vin为电容C1及耦合电感原边充电,漏感电流开始线性上升,同时耦合电感副边电流线性下降;在t5时刻,耦合电感原边能量释放完毕,副边电流降为0,二极管D3电流下降至0,实现零电流关断,此模态时间较短。在此模态下,励磁电感电流和漏感电流分别为
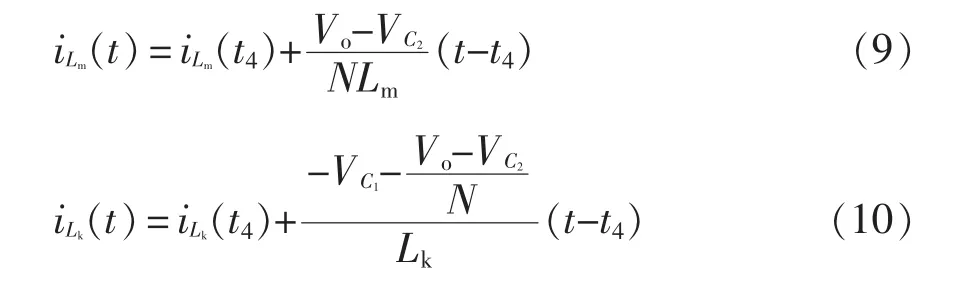
3 变换器工作性能分析
3.1 电压增益分析
已知耦合电感的耦合系数k=Lm/(Lm+Lk),匝比N 为N=n2/n1,为了便于稳态分析,只考虑模态Ⅰ和模态Ⅲ。当变换器工作在工作模态Ⅰ时情况,根据图4(a),得出励磁电感电压、耦合电感副边电压Vn2以及输入电感电压之间的关系,即
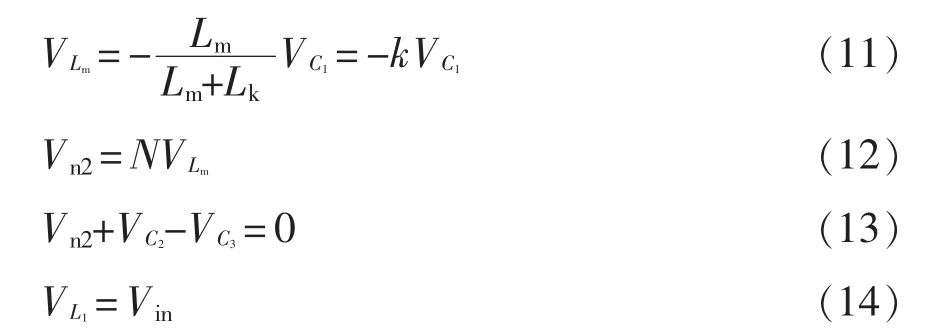
当变换器工作在工作模态Ⅲ时,根据图4(c)得
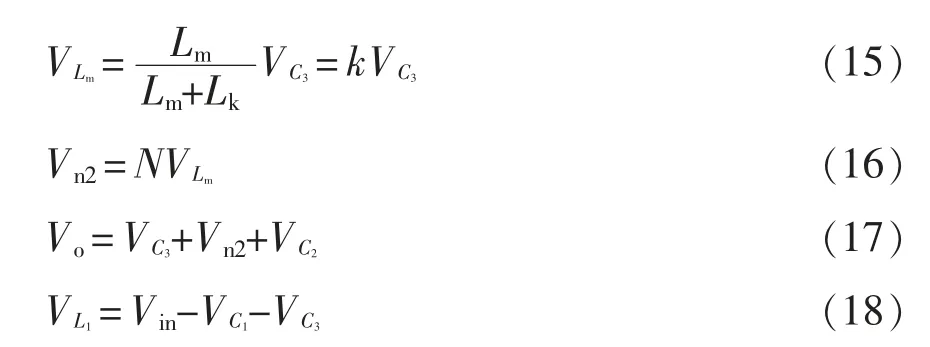
根据耦合电感的励磁电感Lm的伏秒平衡原理,在占空比为D 的条件下有

由式(11)、式(15)、式(19)得到电容C1和C3的电压关系为

由电感L1的伏秒平衡原理,得

将式(14)、式(18)代入式(21),得到输入电压和电容C1电压的关系为

由式(20)、式(22)可得

由式(11)、式(12)得耦合电感副边电压为

由式(13)、式(23)、式(24)得电容C2的电压为

将 式(15)、式(16)、式(23)、式(25)代 入 式(17),得到变压器输出电压为

变换器的电压增益表达式为

当k=1 时,变换器的电压增益表达式为
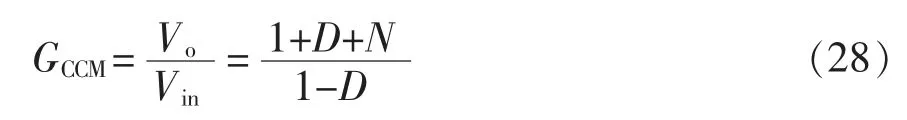
当k=1、不同匝比N 时,变换器电压增益GCCM与占空比D 之间的关系如图5 所示。可以看出,当N 不断增大时,变换器的电压增益不断提升,通过调节D 可灵活调节变换器的电压增益。

图5 k=1、不同匝比N 时变换器电压增益与占空比之间的关系Fig.5 Relationship between the converter’s voltage gain and duty cycle ratio under different values of turns ratio N when k=1
由于耦合电感漏感Lk对变换器的占空比D 存在一定的影响,分析当D=0.6 时,变换器的增益GCCM与不同匝比N 和耦合系数k 之间的关系[24],其三维曲面图如图6 所示。可见,当N 取固定值时,k 越大,变换器的电压增益越高,D 越大,所以在变换器设计的实际应用场合下,应尽量选取k=1。
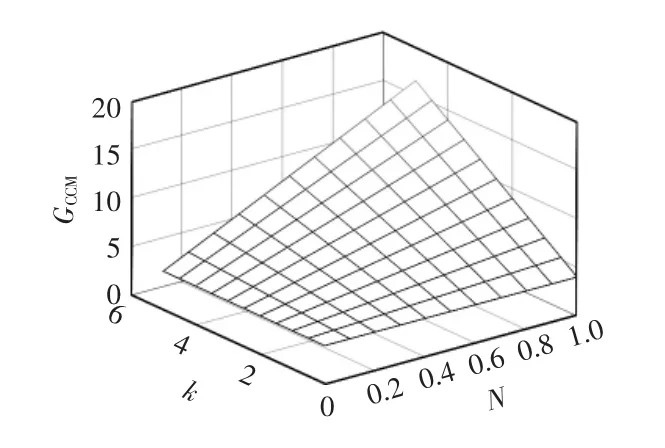
图6 D=0.6 时变换器电压增益与匝比N 和耦合系数k之间的关系Fig.6 Relationship among the converter’s voltage gain,turns ratio N and coupling coefficient k when D=0.6
3.2 电压应力分析
电压应力是选择器件的重要依据。为了简化分析,假设耦合电感的耦合系数k=1,得到电容C1、C2、C3及输出电容C4的电压应力分别为
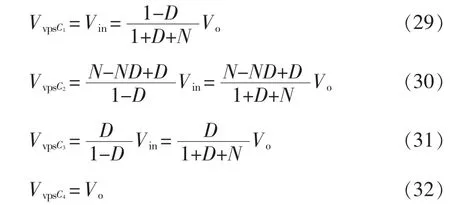
开关管S 的电压应力为
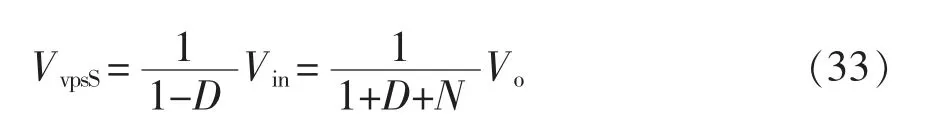
二极管D1、D2、D3的电压应力分别为

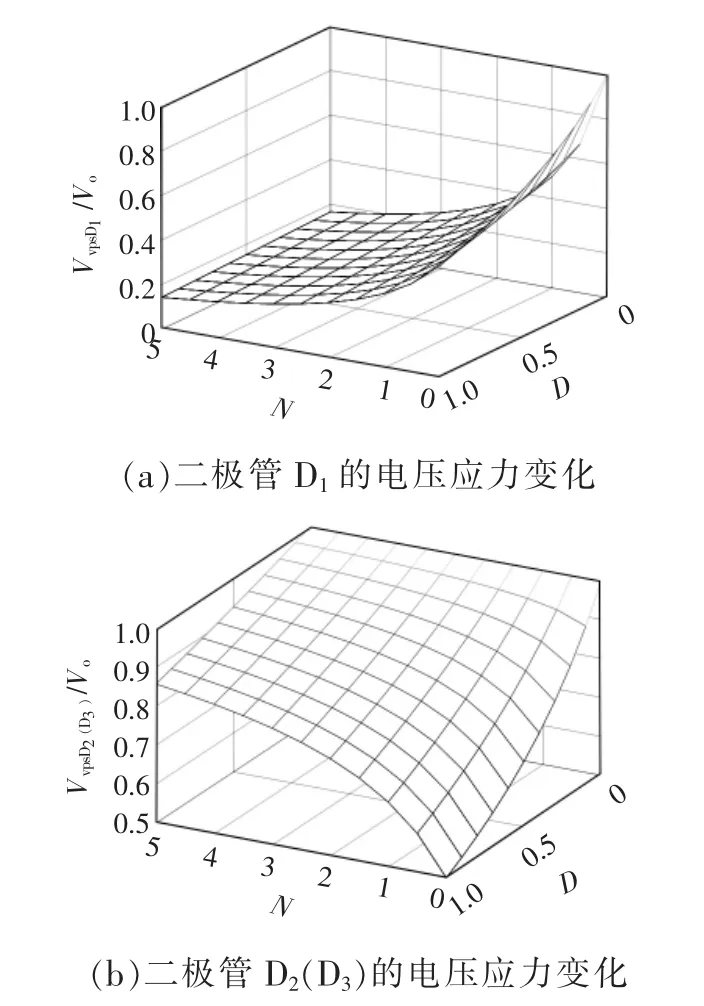
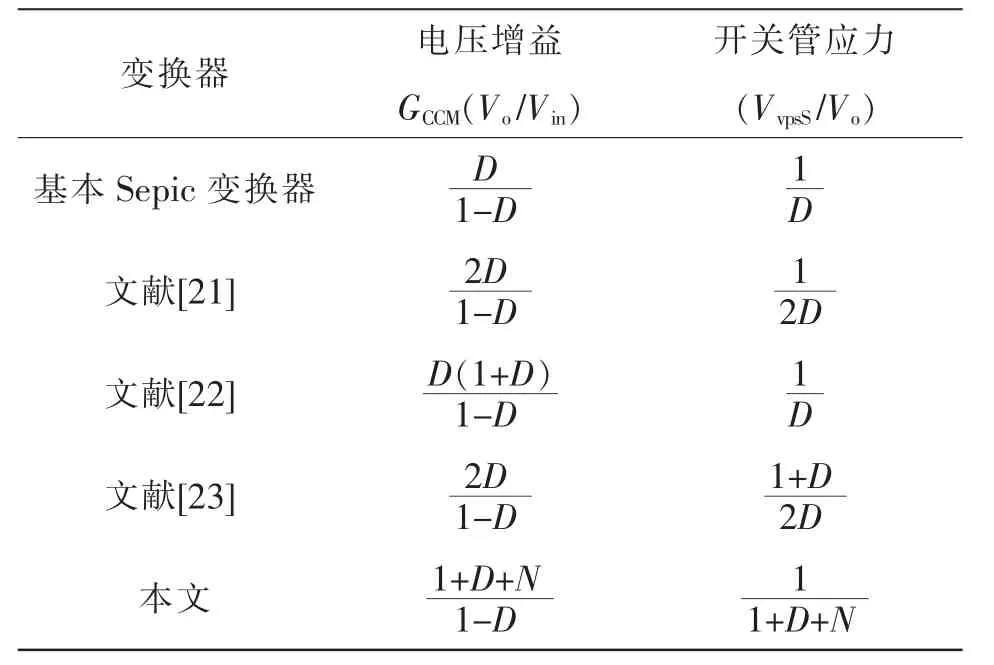
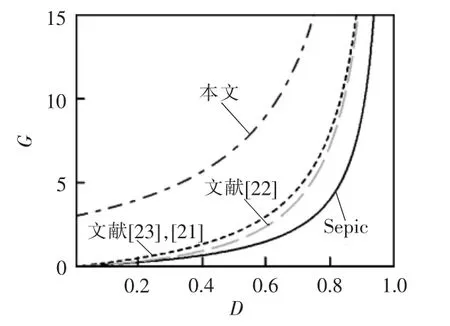
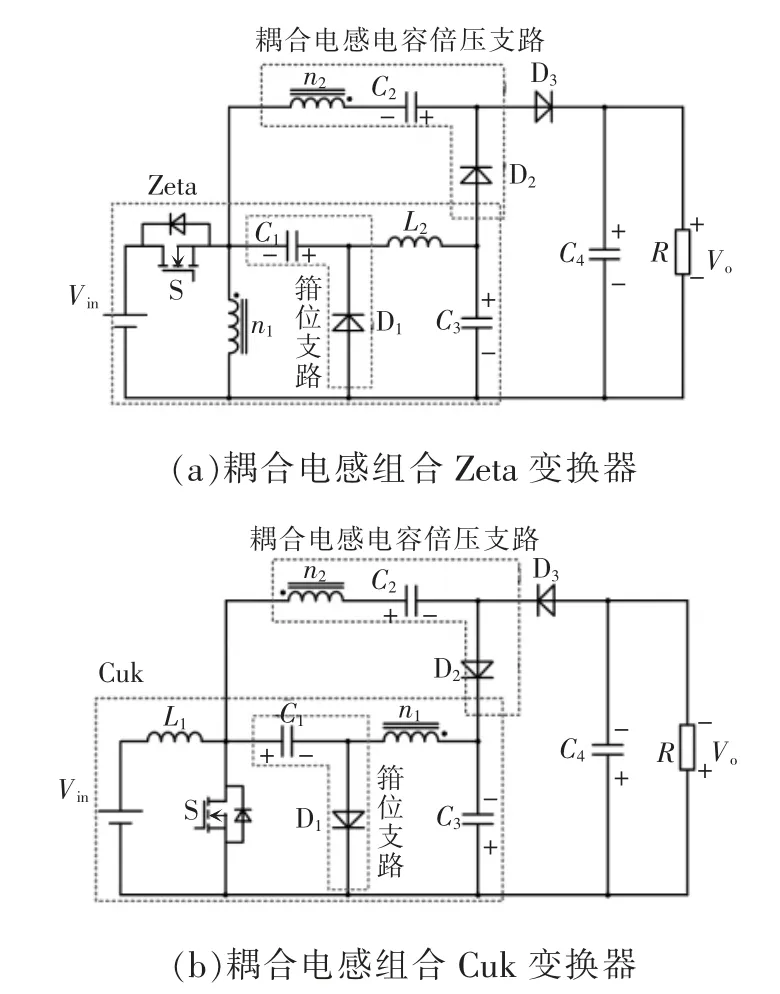
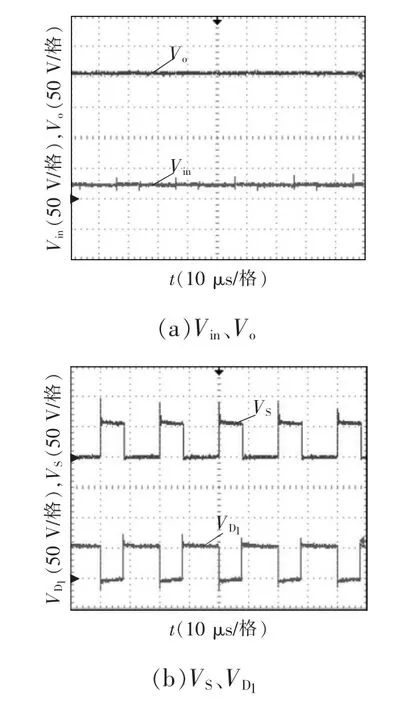
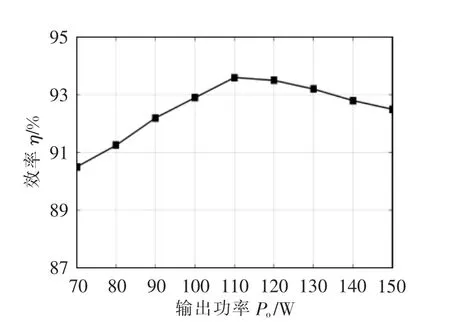
图7 为电容C1、C2、C3和开关管S 及电压应力与输出电压之比和N 与D 之间关系的三维曲面图。由电容电压应力变化趋势可知,随着N 的增加,C1、C3的电压应力明显减小;同时,随着D 的增大,C1的电压应力减小,C3的电压应力增加。对于C2两端的电压应力随N 的变化趋势,当0 图7 电容C1、C2、C3 及开关管S 的电压应力与匝比N 和占空比D 的关系Fig.7 Relationship among voltage stress of capacitors C1,C2,C3 and switching tube S,turns ratio N and duty ratio D 图8 为二极管D1、D2、D3的电压应力与匝比N和占空比D 的关系。由各二极管两端电压应力的变化趋势可知,随着N 的增加,二极管D1的电压应力减小,二极管D2、D3的电压应力上升;而随着D 的增加,二极管D1、D2、D3两端的电压应力均减小。由此在设计选定变换器参数时,应考虑匝比对电压应力的影响,合理选择各功率器件的型号。 图8 二极管D1、D2、D3 的电压应力与匝比N 和占空比D的关系Fig.8 Relationship among voltage stress of diodes D1,D2 and D3,turns ratio N and duty ratio D 将本文所提耦合电感组合Sepic 变换器与基本Sepic 变换器、文献[21]的磁集成组合式Sepic 变换器文献[22]所提出的加入输入开关电感单元的Sepic变换器,以及文献[23]所提出的在开关电感单元间加入耦合电感的Sepic 变换器的性能进行对比,结果如表1 所示。 表1 变换器性能参数对比结果Tab.1 Comparison results of performance parameters among different converters 当匝比N=2 时5 种Sepic 变换器的电压增益随占空比D 的变化曲线如图9 所示。由图可以看到,各变换器的电压增益均随占空比D 的提高而增大;文献[21]、[22]以及[23]所提出的Sepic 变换器,其增益相较于基本Sepic 变换器均有明显提升;本文所提高增益耦合电感组合Sepic 变换器的电压增益最高,且增益性能优于其他变换器,随占空比D的变化增益的上升幅度较大,从而更易在保证高增益的条件下选择更适宜的占空比。 图9 变换器增益对比Fig.9 Comparison of gain among different converters 当匝比N=2 时各变换器开关管电压应力的变化趋势如图10 所示。由图可见:基本Sepic 变换器及文献[22]所提变换器的开关管电压应力大于输出电压;文献[21]和文献[23]所提变换器的开关管电压应力随占空比D 的增大而减小,其电压应力比基本变换器的有所减小;本文所提变换器的开关管电压应力减小明显,达到了很低的数值,由此则可以在保证变换器高增益的同时,选取具有电压应力更低的电力MOSFET,可以有效降低成本。 图10 开关管电压应力对比Fig.10 Comparison of voltage stress among different switching tubes 变换器的2 种拓展形式如图11 所示。由于Zeta、Cuk 变换器与Sepic 变换器具有相似的电路结构(LCD 单元)与工作原理,故可将耦合电感组合Sepic 变换器改造思想运用于Zeta、Cuk 变换器,将Zeta、Cuk 变换器作为基底,同时将其二极管-电容支路作为箝位吸收回路,得到图1 的耦合电感组合Zeta 变换器和耦合电感组合Cuk 变换器。该变换器的改造思想也可应用于其他变换器,在此不再赘述。 图11 变换器的2 种拓展形式Fig.11 Two expansion forms of converter 为验证本文所提新型高增益耦合电感组合Sepic 变换器原理的正确性,制作了一台实验样机,如图12 所示。实验样机平台耦合电感采用罐型磁芯GU30,独立电感采用罐型磁芯GU36,主电路参数如表2 所示。 表2 变换器主电路参数Tab.2 Main circuit parameters of converter 图12 实验测试平台Fig.12 Experimental test platform 输入、输出电压及各器件电压应力波形如图13所示。图13(a)为变换器的输入、输出电压波形,可以看出,变换器实现了输入电压24 V、输出电压200 V 的高增益变换;图13(b)为开关管S 与二极管D1的电压应力波形,图13(c)为二极管D2与D3的电压应力波形,可以看出,在输出电压为200 V的情况下,开关管电压应力约为60 V,远远小于输出电压,具有较低的电压应力;二极管D1电压应力与开关管S 的接近,而二极管D2、D3的电压应力虽大于开关管S 的电压应力,但依然小于输出电压。 图13 输入、输出电压及各器件电压应力波形Fig.13 Waveforms of input and output voltage and voltage stress of each device 耦合电感原、副边及各器件的电流波形如图14 所示。图14(a)为耦合电感漏感原副边电流,图14(b)为电感L1与二极管D1的电流,图14(c)为二极管D2和D3的电流,可以看出,二极管D1实现零电流关断,二极管D2和D3都实现零电流开通。各项实验结果均验证了理论的正确性。 图14 耦合电感原、副边及各器件电流波形Fig.14 Waveforms of current of coupled inductor on the primary and secondary sides,and current of each device 当变换器满足输入电压为24 V、输出电压为200 V 条件下,随着输出功率的变化,变换器的参考效率曲线如图15 所示。可以看出,变换器功率在110 W 左右达到的最高效率为93.4%。由于变换器没有进行PCB 制板且限于实验平台的影响,变换器效率曲线仅供参考。 图15 变换器效率曲线Fig.15 Efficiency curve of converter (1)将耦合电感与Sepic 变换器相结合,变换器的电压增益可通过耦合电感匝比N 进行调节,可应用于各种高增益场合。 (2)通过共用Sepic 变换器中的二极管-电容支路作为箝位吸收支路,有效抑制了开关管寄生电容与漏感谐振产生的电压尖峰,提高了变换器的效率;开关管的电压应力远远小于输出电压,具有较低的电压应力,可选用低电压等级的开关器件。 (3)将耦合电感与二极管-电容倍压单元组合改造方案应用于耦合电感组合Zeta、Cuk 等变换器中,具有普遍应用价值。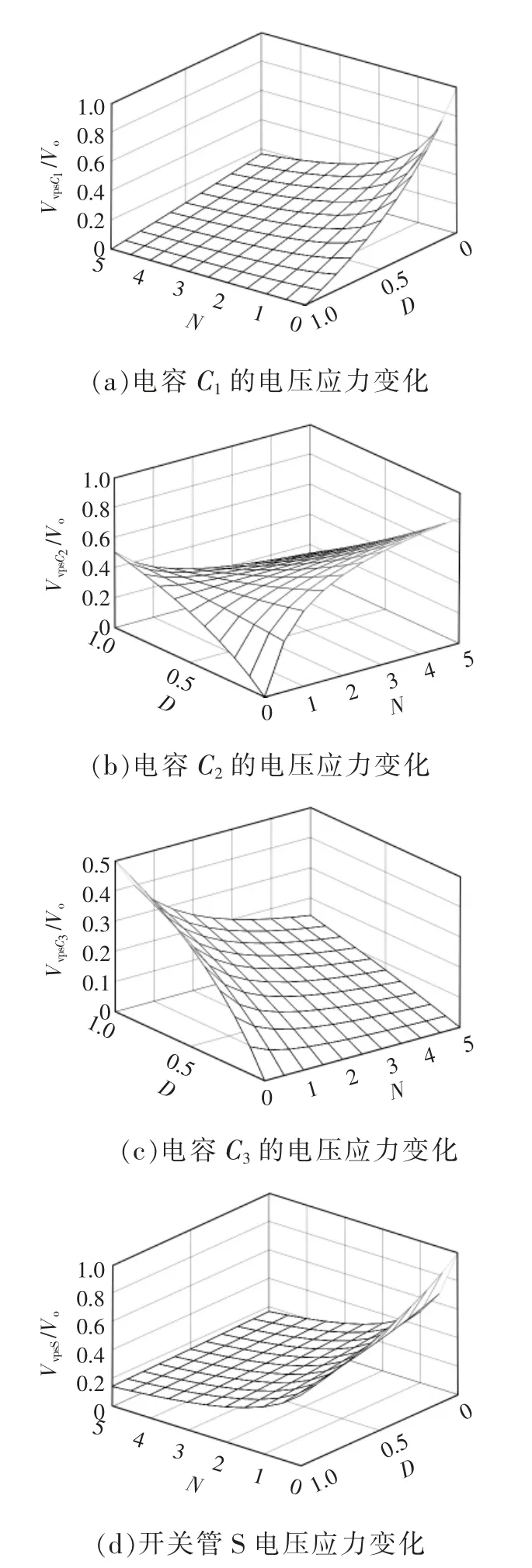
4 变换器的性能对比

5 同类变换器拓展
6 实验结果分析




7 结论

