基于柔性电感的恒频控制LLC 谐振变换器
王 锐,阚加荣
(1.江苏大学电气信息工程学院,镇江 212013;2.盐城工学院电气工程学院,盐城 224051)
利用新能源发电是解决能源危机和环境污染等问题的重要举措,其中光伏发电被认为是较为安全可靠、高效率、低成本的可再生能源利用方式[1]。在并网型光伏发电系统中,为了给后级逆变器提供稳定的直流电压,通常在发电单元与逆变器之间加入DC-DC 变换器实现逆变器的稳定供电。
典型的脉冲宽度调制PWM(pulse width modulation)直流变换器是在硬开关状态下工作的,存在开关损耗,且对周围设备存在电磁干扰,限制了开关电源频率的提高和应用场合,因此软开关技术开关电源得到广泛应用。目前已有大量文献针对软开关包含了LC 串联和并联、LCC[2]、LLC 谐振变换器的拓扑结构进行深入研究。其中:LC 串联和并联谐振变换器缺点较多,限制了其工程运用;LCC 变换器多用于高压输出场合;LLC 谐振变换器由于高频、高效率及高功率密度的特征,成为研究热点。
LLC 谐振变换器由于能够在全负载范围内实现原边开关管的零电压导通ZVS(zero voltage switching)及副边整流二极管的零电流关断ZCS(zero current switching)[3],当输入电压和负载变化时,通过改变变换器的开关频率实现输出电压的稳定。如果变换器的输入电压范围较宽,由于LLC 谐振变换器的固有特性,变换器的开关频率需要在较宽的范围内调节,宽范围工作频率将导致LLC 变换器的磁性元件难以优化设计[4-5]。文献[6]提出移相控制策略,该方法下开关频率保持固定,有利于磁性元件优化,但存在占空比丢失、增益计算过程复杂的缺点;在此基础上,文献[7]将变频控制与移相控制相结合,提出一种混合控制策略,有效改善了上述问题,但在宽输入电压、宽负载条件下,仍存在开关频率变化范围较宽、增益计算复杂等问题;文献[8]提出一种通过附加开关改变谐振电路电容的控制方法,可以使开关频率保持恒定,但该方法的开关电容控制电路及电容变化计算较复杂。
本文在LLC 谐振变换器中引入柔性电感,通过改变其值来改变谐振单元的谐振频率,从而改变LLC 谐振变换器的输出特性,实现LLC 变换器的恒频控制,为变换器磁性元件的优化设计提供条件。
1 LLC 谐振变换器的基本原理和工作特性
图1 为全桥LLC 谐振变换器的主电路拓扑结构,其中开关管S1~S4构成全桥逆变器,谐振电感Lr、谐振电容Cr及励磁电感Lm构成谐振网络,整流二极管DR1、DR2和电容Cf1、Cf2构成倍压整流器。图1 中,为流过谐振电感Lr的电流,为变压器励磁电流,uAB为谐振网络输入电压,为谐振电容两端电压,Np、Ns分别为变压器的原边、副边绕组匝数。
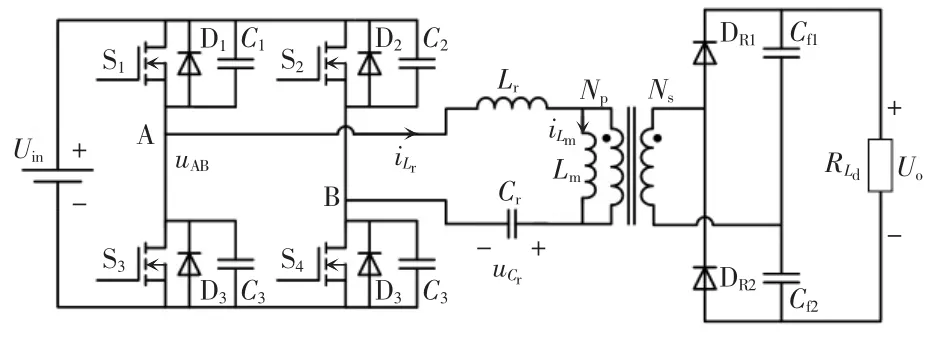
图1 全桥LLC 谐振变换器的主电路拓扑Fig.1 Main circuit topology of full-bridge LLC resonant converter
LLC 变换器谐振网络中,励磁电感Lm会出现被变压器副边电压箝位而不参与谐振过程,因此LLC变换器工作中存在2 个不同频率的谐振过程。当Lm被箝位时,Lr和Cr谐振,此时的谐振频率fr为

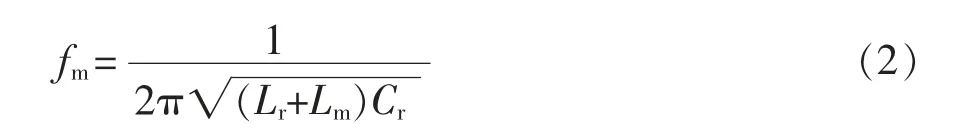
根据开关频率fs与这2 个频率间的关系,变换器存在4 种工作模态:①当fs≤fm时为谐振模式,变换器的谐振网络呈容性,原边开关管无法实现ZVS,因此LLC 谐振变换器应避免工作在此范围内;②当fm<fs<fr时为欠谐振模式,变换器的谐振网络呈感性,开关管可以实现ZVS,副边整流二级管可实现ZCS 关断;③当fs=fr时为临界谐振模式,工作情况与第②种相似,开关管仍能实现ZVS,仅缺少了Lm参与谐振的阶段,DR1和DR2的电流处于临界连续导通状态,整流二极管仍能实现ZCS;④当fs>fr时为过谐振模式,Lm在整个过程中被副边电压箝位而不参与谐振,开关管仍能实现ZVS,但是整流二极管处于连续导通模式,不能实现ZCS,但会出现反向恢复问题,损耗较小。
综上所述,在fm<fs≤fr频率范围内,变换器不仅能实现原边开关管的ZVS,也能实现副边整流二极管的ZCS,是最佳工作范围,设计时应尽量使变换器工作在此范围内。
将变换器输出/输入电压增益函数M 定义为

式中:n 为变比,n=NP/NS;Uin和Uout分别为谐振变换器输入电压和输出电压。
为了实现效率最优,通常将LLC 谐振变换器的开关频率设计在谐振频率fr附近。此时,谐振网络输入电压的高次谐波对变换器影响不大,可以忽略。因此,可采用基波分量简化法分析变换器的特性[9]。
LLC 谐振变换器等效线性电路如图2 所示,其中Ui、Uo为输入和输出电压的基波有效值,R 为负载折算到变压器原边侧的等效电阻,计算公式为


图2 谐振网络简化电路Fig.2 Simplified circuit of resonant network
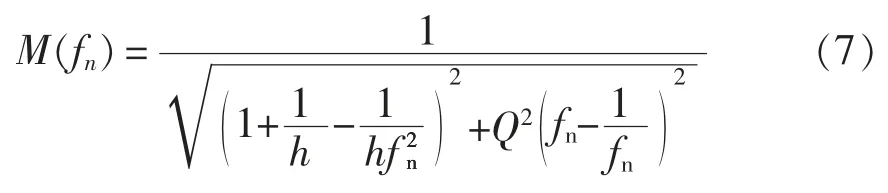
式中:h 为励磁电感与谐振电感的比值,h=Lm/Lr;Q为谐振品质因数,Q=Zr/R;fn为归一化频率,fn=fs/fr。
根据式(7),选定h 后,不同负载相应的电压增益曲线如图3 所示。可以看出,当fn=1 时,电压增益与负载无关,电压增益恒等于1,原因为此时谐振电感与谐振电容间的谐振阻抗为0,激励源直接加在变压器的原边侧。纯阻性曲线与fn=1 将增益曲线划分为3 个区域,区域Ⅰ和Ⅱ可以实现原边开关管的ZVS,区域Ⅱ和Ⅲ可以实现副边整流二极管的ZCS。因此,设计时应尽量使其工作在区域Ⅱ,此时效率较高[11]。
从图3 可以看出,当输入电压和负载变换范围宽时,LLC 谐振变换器的开关频率变化范围宽,磁性元件难以优化设计。
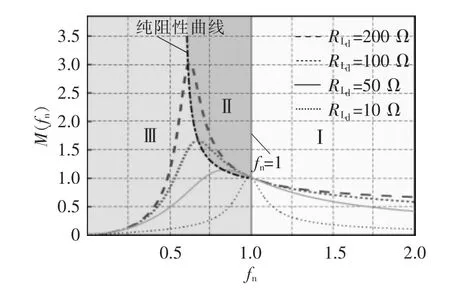
图3 频率比与电压增益曲线Fig.3 Curves of voltage gain versus frequency ratio
2 柔性电感LLC 谐振变换器的原理与设计
2.1 柔性电感LLC 谐振变换器的基本特性
根据变频控制LLC 谐振变换器基本特性的分析,在确定变换器开关频率fs及LLC 谐振网络中谐振电容Cr后,可算出在该开关频率下的临界谐振电感Ls,即

根据式(7)和式(8),采用柔性电感时的LLC 谐振变换器增益特性为
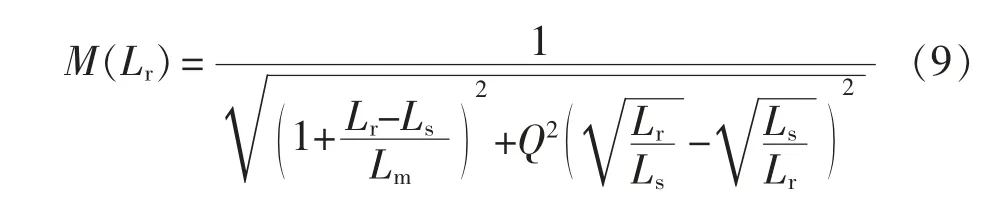
根据式(9),确定Lm后,不同负载相应的电压增益曲线。柔性电感增益曲线与其感值范围如图4所示。从图4(a)可以看出,当Lr/Ls=1 时,电压增益与负载无关,电压增益恒等于1,表明可以将柔性电感作为输出电压的控制参数。纯阻性曲线与直线Lr/Ls=1 将增益特性曲线划分为3 个区域,其中:区域Ⅰ和Ⅱ可实现原边开关管的ZVS;但区域Ⅰ不能实现副边整流二极管的ZCS,在关断时有反向恢复问题,增大了损耗。因此,在设计时应尽可能使其工作在区域Ⅱ。
根据Lr与M 的关系以及所需要M 的范围,可确定出Lr的变化范围,如图4(b)所示。本文所设计变换器电压增益范围为1.028~1.565,则所需Lr的范围为10.7~26.5 μH,减去变压器原边漏感,可得设计所需柔性电感范围为9.1~24.9 μH。
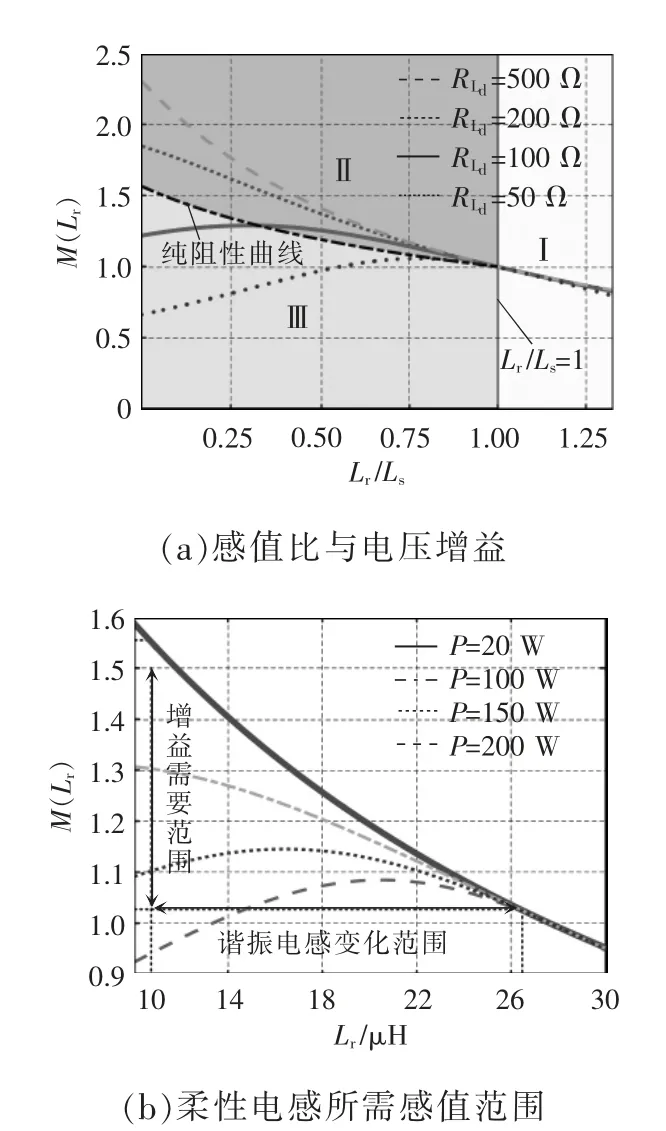
图4 柔性电感增益曲线与感值范围Fig.4 Gain curve and inductance range of flexible inductor
2.2 柔性电感的原理与设计
柔性电感采用带有气隙的EE 型铁芯实现,其原理和等效电路如图5 所示。
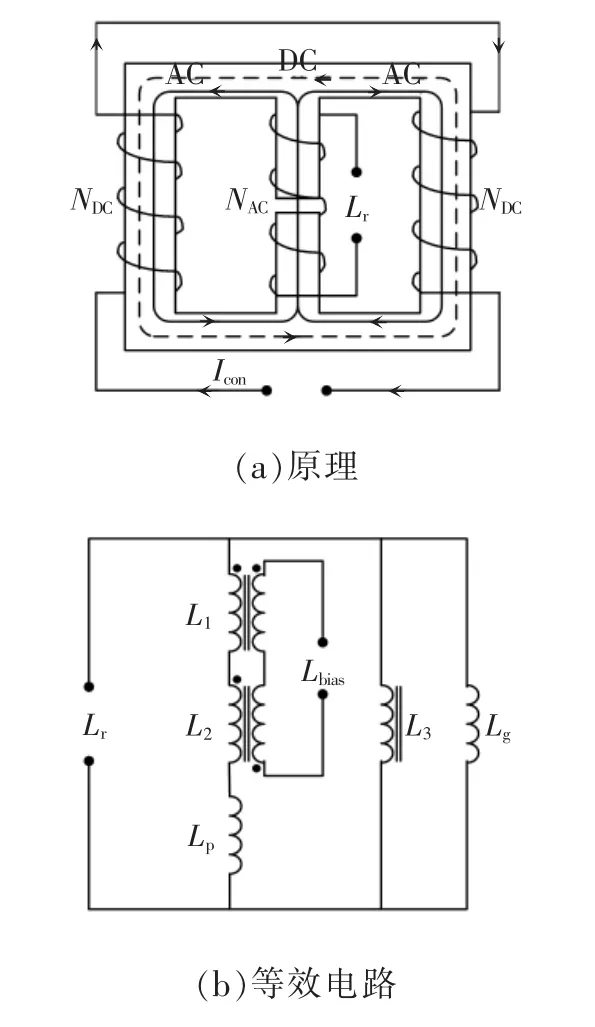
图5 柔性电感原理与等效电路Fig.5 Principle and equivalent circuit of flexible inductor
柔性电感原理如图5(a)所示,其中心柱上绕主线圈,构成图1 中的谐振电感Lr,通工作用交流电;两臂的磁芯柱上分别绕匝数相等的磁偏置绕组,通控制所需直流电。磁偏置绕组中通控制电流Icon后,左右臂磁芯柱上的磁偏置绕组会在铁芯中产生大小相等的磁通,两臂的磁通方向相同,相互叠加,产生磁偏置;中心柱上的磁通方向相反,相互抵消。因此,柔性电感的实质就是通过改变Icon的大小改变铁芯的磁饱和程度,从而改变Lr,实现电感调节。
图5(b)为柔性电感的等效电路。图中,L1、L2分别为左右两臂绕组产生的等效电感,当通电流Icon时,偏置电感Lbias改变,引起L1、L2变化;L3为中心柱绕组产生的电感;Lg、Lp分别为气隙及漏磁通产生的电感[12]。由图5(b)可得等效电感为
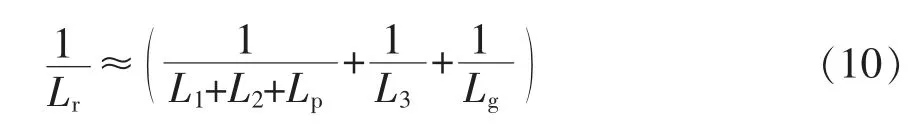
则各部分电感可分别求得,即

式中:A1、A3分别为铁芯侧臂与中心柱截面积;l1、l3分别为左臂磁路与中心柱磁路长度;lg为气隙长度;n3为中心柱上线圈匝数;u0为真空磁导率;ui为初始磁导率;为左右两臂磁芯柱在偏磁作用下铁芯的相对磁导率[13]。
在设计时需注意,电感最大、最小值比与中心柱磁路长度及气隙长度比(l3/lg)相关,其关系可表示为

柔性电感的最大值与偏置绕组无关,可通过电感的基本方程求得,即

式中:Urms为柔性电感两端电压的有效值;ΔBm为磁通密度增量。
由式(16)和式(17)可得所需铁芯体积的估计值为
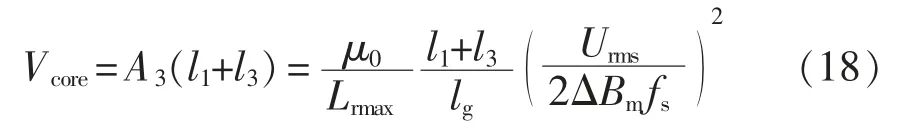
根据图5(b),所需柔性电感的最大值为24.9 μH。由式(15)可以看出,若所需柔性电感的变化范围较大,则气隙要求很小,这可能会造成铁芯饱和;而为减小铁芯损耗,应使磁通密度增量ΔBm较小,则需要较大的气隙。考虑柔性电感与控制电流间的变化关系,选定Lrmax/Lrmin=5,相应得:Lrmax=24.9 μH,Lrmin=5.0 μH。
根据参数要求,选择材料PC40 的EE33 型铁芯设计柔性电感,通过查询数据手册得其基本参数:l1=l2=0.052 m,l3=0.024 m,lg=0.3 mm,A1=A2=6.1×10-5m2,A3=1.22×10-4m2。为满足柔性电感的电感值变化要求,主线圈的匝数需要根据电感最大值确定,由式(16)可得主线圈绕组的匝数n3=7,则柔性电感的最大值为25.04 μH[17]。此外,所需Icon与柔性电感偏置绕组的匝数相关,因此在设计时,使用Nb1=Nb2=120匝、直径0.15 mm 的漆包线绕制偏置绕组[14]。
由于柔性电感与铁芯的材料和尺寸、气隙及磁路长度等因素相关,因此需要通过实测确定控制电流与电感间的关系。图6 为所设计柔性电感的实物图及相应的电感测量曲线。从电感曲线可以看出,当控制电流Icon在0~0.1 A 之间变化时,电感变化明显;当Icon在0.1~0.2 A 之间变化时,电感变化缓慢。由于所设计柔性电感的变化范围为9.1~24.9 μH,则所需控制电流变化范围为0~0.11 A。其中,Icon通过线性调节器得出,不会产生过多的能量损耗。


图6 感值可变的柔性电感实物与电感曲线Fig.6 Prototype and inductance curve of flexible inductor
2.3 恒频控制的闭环实现方案
采用柔性电感后,变换器可以采用恒频控制策略,即通过改变柔性电感改变增益,实现调压。恒频控制闭环电路及电压控制电流源电路如图7 所示。

图7 恒频控制闭环电路及电压控制电流源电路Fig.7 Closed-loop circuit of constant-frequency control and voltage controlled current-source circuit
图7(a)为恒频控制的闭环实现电路,将输出电压采样后反馈,与基准电压通过PI 调节得到误差电压作为控制电压Ucon。Ucon经图7(b)所示的电压控制电流源电路得到控制电流Icon,通过改变Icon改变Lr,实现闭环。图中,驱动电路、采样电路、PI 调节和输出电路均通过DSP 实现。
3 实验研究
为了验证所提设计理论的正确性,本文设计了一台基于柔性电感的LLC 变换器原理样机。具体参数如下:直流输入电压23~35 V,输出电压Uo=100 V,最大输出功率200 W;开关频率fs=40 kHz,谐振电容Cr=570 nF,谐振电感(包括变压器原边漏感L1k=1.6 μH)的变化范围为10.7~26.5 μH,变压器副边漏感L2k=2.8 μH,励磁电感L2=46.76 μH,变压器匝比n=0.706。根据光伏电池输出特性,设定最大负载功率与输入电压间的关系如图8 所示。
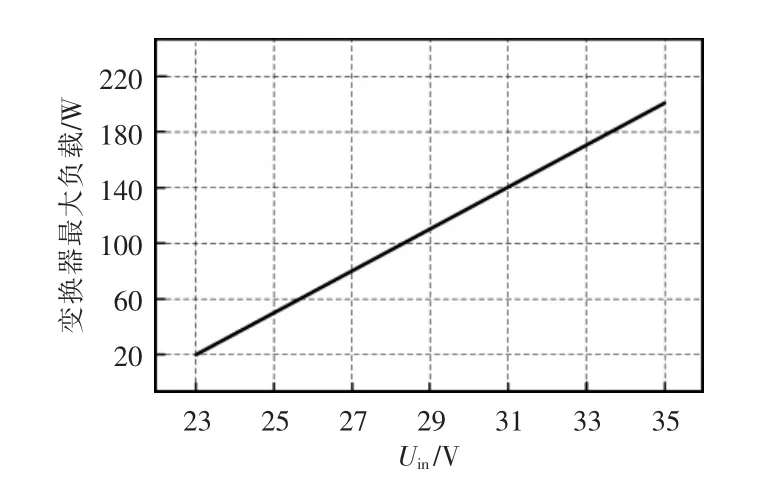
图8 变换器承受最大负载与输入电压间关系曲线Fig.8 Curve of relation between maximum load and input voltage of converter
恒频控制实验波形如图9 所示。图9(a)、(b)分别为输入电压23 V 和35 V、负载20 W 时变换器在恒频控制策略下的主要实验波形,其中uGS1、uDS1和uGS2、uDS2分别为开关管1、2 的驱动电压和漏源电压。可以看出,Uin越大,、的波形越接近临界谐振模式下的波形。当Uin为23 V 时,实际测得Icon为0.097 A,根据图7 的柔性电感曲线得Lr为11.25 μH;增大Uin为35 V 时,测得Icon为0.025 A,对应的Lr为24.6 μH。
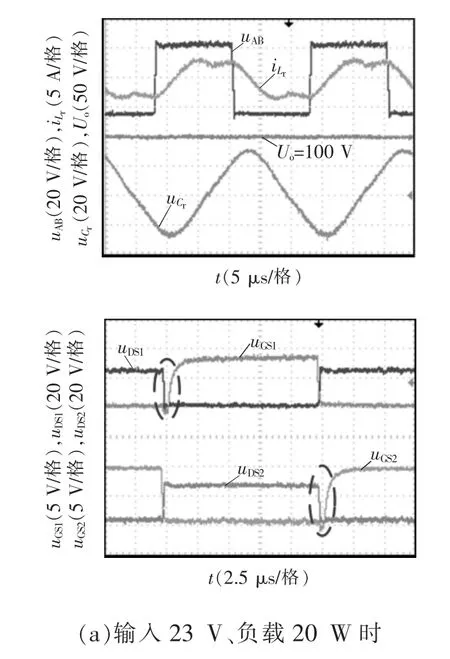

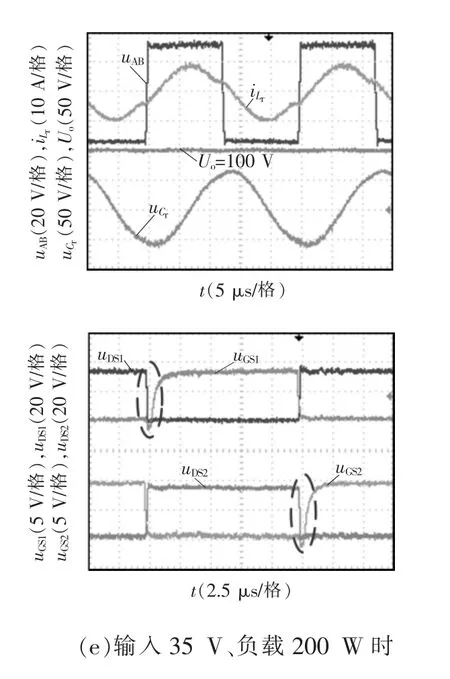
图9 恒频控制实验波形Fig.9 Experimental waveforms under constantfrequency control
图9(c)、(d)分别给出输入电压28.3 V 和35 V、负载100 W 时变换器的实验波形。可以看出,随着负载增大,、均增大。当Uin为28.3 V 时,实际测得Icon为0.094 A,可得Lr为12 μH;增加Uin到35 V 时,测得Icon为0.04 A,对应的Lr为23 μH。
图9(e)为输入电压35 V、负载200 W 时变换器的实验波形。此时,测得Icon为0.06 A,可得对应的Lr为19.3 μH。
由图9 可以看出:在不同的输入电压及负载条件下,恒定开关频率下输出电压均稳定在100 V,且谐振电流滞后于谐振网络输入电压,谐振网络呈感性,变换器均工作在欠谐振模式;开关管导通前漏源电压已经下降至0,实现了ZVS。由此,在要求的输入电压与负载范围内,基于柔性电感的LLC 谐振变换器在恒频稳压控制下实现了所有开关管的ZVS。
4 结论
在分析全桥LLC 谐振变换器变频控制原理及工作特性的基础上,引入柔性电感,将电感值作为变换器输出电压调节的控制参数,提出一种恒频控制的LLC 谐振变换器,并给出其具体实现方法。通过一台输入电压23~35 V、输出电压100 V、功率200 W 的样机进行了实验研究,表明了所提出的变换器具有以下性能:
(1)在宽输入电压、宽负载范围内,变换器能实现稳定调压。
(2)在全输入范围内,变换器均工作在欠谐振模式,电路损耗小。
(3)在全输入范围内,所有开关管均能实现ZVS,减小了开关损耗。
(4)开关频率保持恒定,易于变压器等磁性元件的优化设计。

