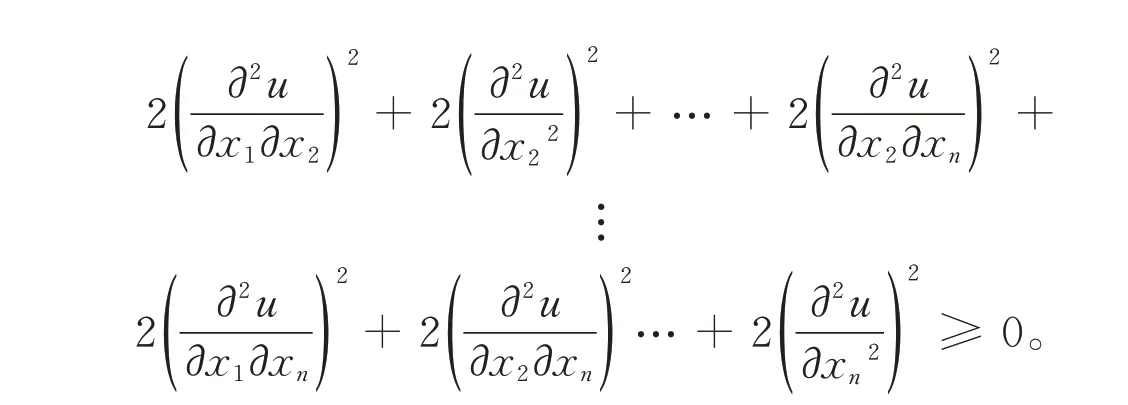下调和函数的性质与判定研究

金庆飞

（江汉大学 人工智能学院，湖北 武汉 430056）

0 引言

调和函数是偏微分方程理论研究中的一类重要函数，很多著作和文献中都指出了调和函数这一重要概念，并对调和函数进行了广泛研究。例如，2009年王明新［1］给出调和函数的定义，并且论证了调和函数的基本积分公式和调和函数的一些基本性质。2020年孙祚晨等［2］研究了一类Salagean型单叶调和函数，得到了这类函数的拟共形性、凸性和卷积性。2021年李东征等［3］通过构造调和函数的微分算子和积分算子，得到a级星象调和函数类在微分算子和积分算子作用下新的调和函数的单叶半径。2020年董宝华［4］利用Fueter方法构造出了Clifford分析中的调和函数。2020年李玉毛等［5］利用广义Salagean算子定义研究了一类调和函数的系数不等式和极植点。2019年傅冬绵等［6］研究了一类单叶调和函数的拟共形性质。2018年时统业等［7］得到了调和凸函数的积分不等式。2019年孙文兵［8-9］研究了分形集上广义调和拟凸函数的一些积分不等式和调和拟凸函数带参数的Hadamard型分数次积分不等式。2017年陈少林等［10］研究了调和函数的Lipschit2型空间和Poisson方程的解的性质。

下调和函数是调和函数的一个推广。本文对下调和函数作了深入研究，给出并证明了下调和函数的两个重要性质和两个判定方法。为此，我们先给出本文中将会用到的定义。

定义1［1］设Ω⊂Rn是区域（连通开集），函数u∈C2(Ω)，若满足-Δu=0,x∈Ω，则称u为Ω上的调和函数。

定义2［1］设Ω⊂Rn是区域（连通开集），函数u∈C2(Ω)，若满足-Δu≤0,x∈Ω，则称u为Ω上的下调和函数。

1 下调和函数的性质

通过构造辅助函数，利用其单调性及坐标变换，我们可以证明下调和函数具有如下性质。

定理1设u为Ω上的下调和函数，则

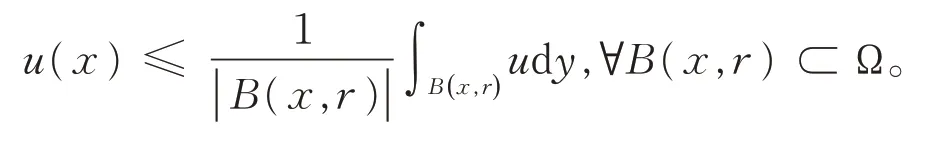
证明 令

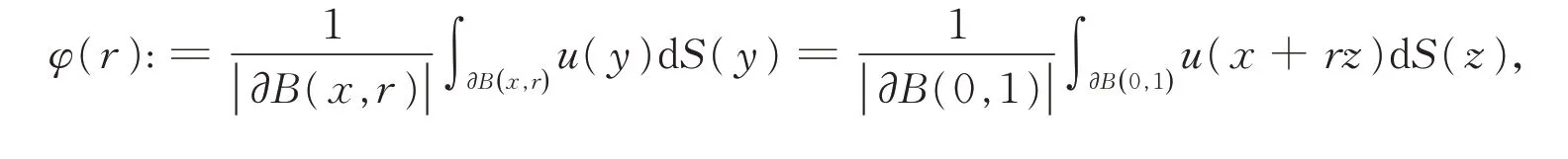
则

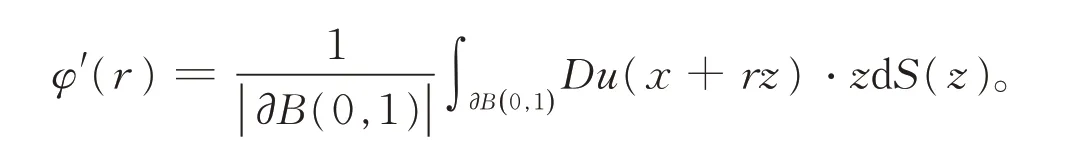
根据格林公式计算可得

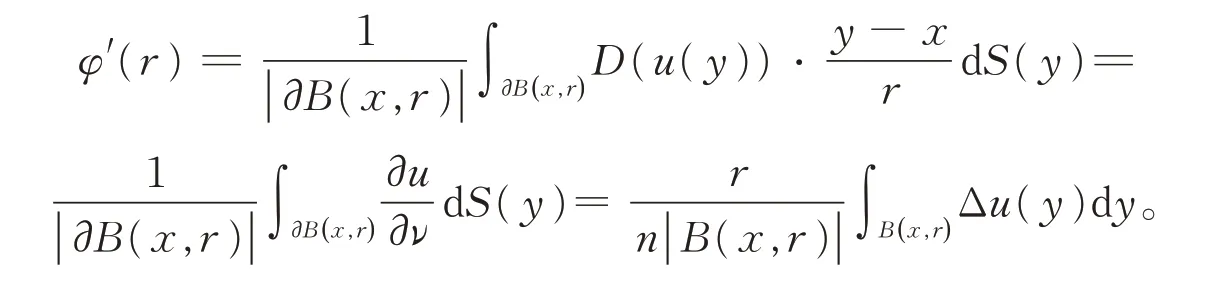
由于-Δu≤0,x∈Ω，所以。因此，φ(r)是关于r的增函数。于是有

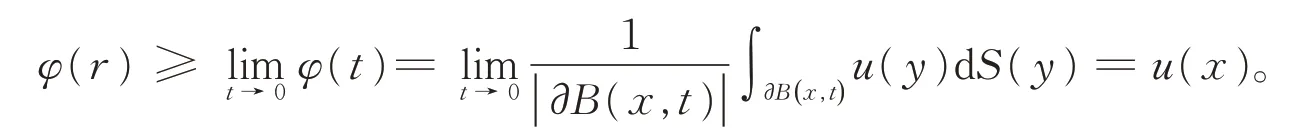
由极坐标变换可得

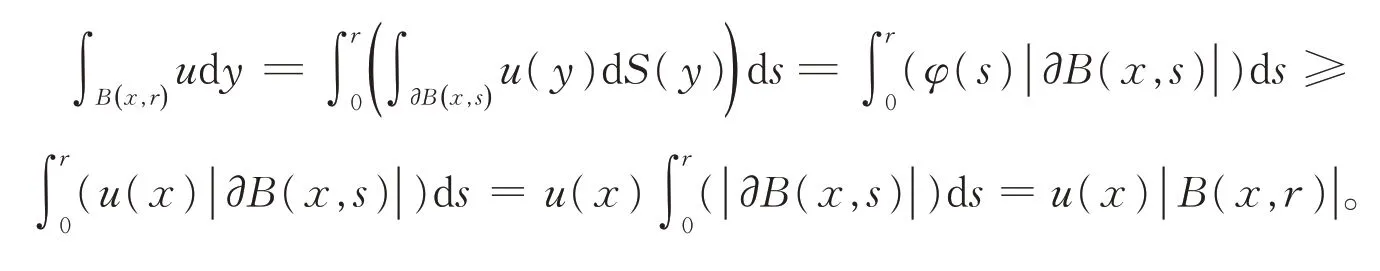
因此

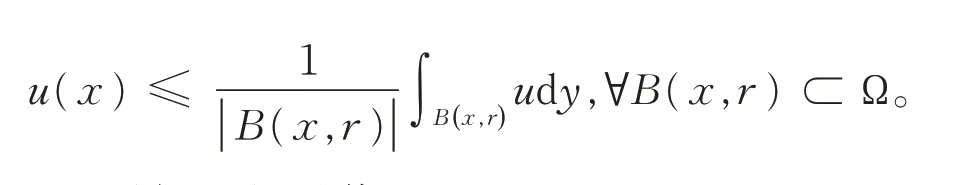
运用反证法，我们可以证明如下的最值原理。

定理2设u为Ω上的下调和函数，则

证明1）u是常数的情形，定理结论自然成立；

2）u不是常数的情形，我们将证明u在Ω内取不到最大值。假设u在x*∈Ω取得最大值M。记ΩM={ }x∈Ω:u(x)=M，则x*∈ΩM。因为u在Ω内连续，所以ΩM是相对闭集。下证ΩM是相对开集。设x0∈ΩM⋂Ω，则x0∈Ω，u(x0)=M。于是，存在ε＞0，使得B(x0,ε)⊂Ω。根据定理1可得

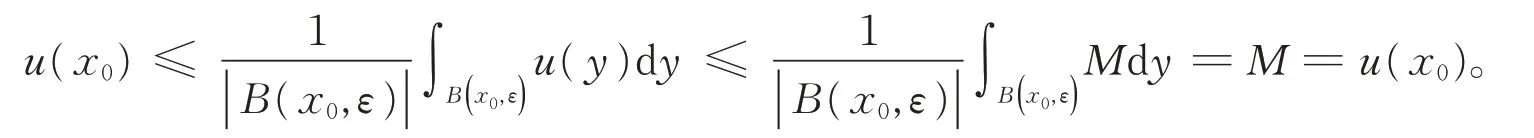
这说明在B(x0,ε)上u(x)≡M，所以B(x0,ε)⊂ΩM。由开集的定义可知，ΩM是相对开集。故ΩM=Ω，从而u是常数。

即证，若u不是常数，则u在Ω内取不到最大值。

2 下调和函数的判定

本小节，我们证明了下调和函数的两个判定方法。

定理3设φ：R→R是光滑的凸函数，u为Ω上的调和函数，则函数v=φ(u)是下调和函数。

证明直接计算可得

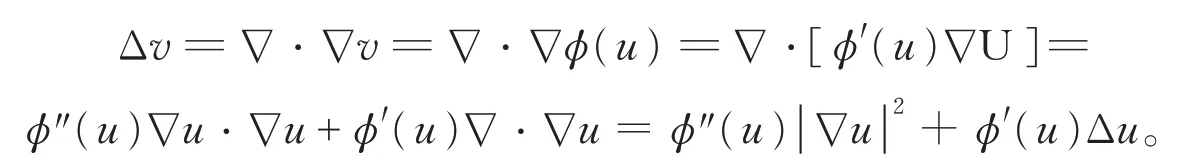
由于φ：R→R是光滑的凸函数，所以φ″(u)≥0。由于u为Ω上的调和函数，所以Δu=0。

于是

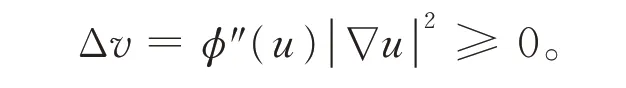
故函数v=φ(u)是下调和函数。

定理4设u为Ω上的调和函数，则是下调和函数。

证明由于u为Ω上的调和函数，所以Δu=0。

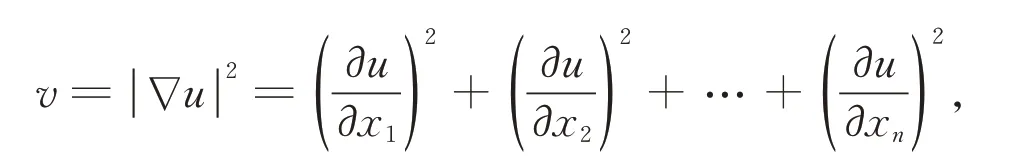
直接计算可得

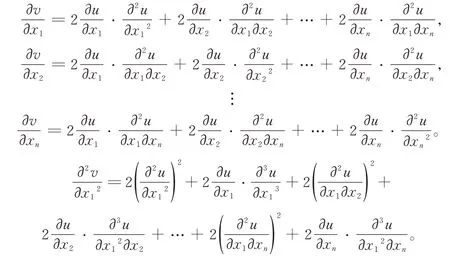
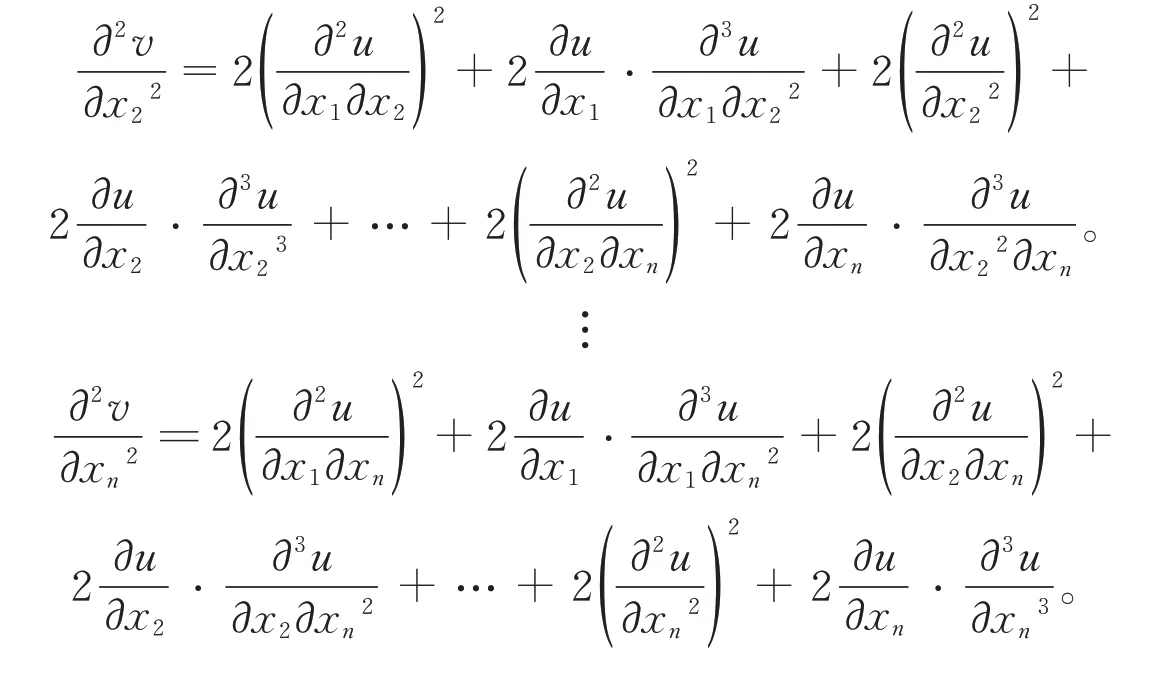
于是