宽大建（构）筑物爆破拆除塌落触地振动速度预测模型

孙金山，颜佳鑫，蒋跃飞，张 震，刘 桐

（1.江汉大学 省部共建精细爆破国家重点实验室，爆破工程湖北省重点实验室，湖北 武汉 430056；2.浙江省高能爆破工程有限公司，浙江 杭州 310000）

0 引言

在城市更新与工业升级改造过程中，大量的楼房、烟囱、冷却塔等建（构）筑物需要被爆破拆除。振动是建（构）筑物爆破拆除过程所产生的主要有害效应之一，拆除爆破中主要产生4种振动，即爆破诱发的振动、后坐诱发的振动、切口闭合诱发的振动、塌落诱发的振动，其中塌落振动占主导地位［1］。因此，工程实践中需要严格控制拆除爆破产生的触地振动效应，而在爆破前对塌落振动效应进行分析预测，并据此制定合理的控制措施是重要的技术环节。

针对拆除爆破塌落体触地振动，周家汉等［2］提出了一种触地振动预测模型，并对其进行了改进。吕淑然等［3］用夯锤自由落体冲击土层产生的振动来模拟塌落体触地产生的振动，并采用量纲分析提出计算公式。王希之等［4］利用能量守恒原理推导出触地振动公式。刘影等［5］分析了桥梁爆破后触地振动对于周围环境和建（构）筑物的影响。孙金山等［6］基于动量守恒理论，将触地冲击过程简化为塌落体与地表塑性区的非弹性碰撞过程，建立了简化的触地冲击力学模型，并根据振动传播规律，提出了触地振动速度的预测公式。目前，对触地振动速度进行准确预测仍很困难，工程实际中，因周家汉等［2］推荐的公式提出较早，但该公式存在力学概念模糊和参数确定困难等问题。而孙金山等［6］提出公式考虑的冲击塑性区范围较大，较适合于烟囱等狭窄结构爆破工程，而对楼房、桥梁等结构的适用性不佳。为此，本文针对触地接触面较宽的楼房、桥梁等结构的拆除爆破工程，建立了基于动量守恒理论的预测模型，并结合工程实例进行了验证分析。

1 塌落触地振动的产生机制

倒塌的建（构）筑物冲击地面过程中，接触面以下的有限岩土介质在短时间内受冲击而发生变形并获得初速度，同时向周围岩土介质中进一步传递动能，最终引起大范围地基及附属物的振动。在冲击发生的过程中，建（构）筑物塌落体与有限体积发生变形的土体是封闭系统，符合动量守恒的条件。因此，触地冲击诱发振动的过程可视为：地面介质受到塌落体撞击后发生屈服，以变形能的形式消耗塌落体的一部分动能；地面介质同时还获得一定初速度，以动能的形式获得塌落体的另一部分动能；在土体弹塑性界面上，质点的扰动向其周围无限介质中传播，诱发周围质点的振动，并耗散掉剩余的动能。

塌落体与地面的碰撞过程应属于典型的非弹性碰撞，即在碰撞冲击过程中，塌落体速度降低至接近0，并将动量传递给地面的土体。在此过程中，可将塌落体简化为具有一定质量和速度的物体，而接触面下的发生塑性变形的土体则作为塌落体碰撞的对象，发生塑性变形的土体与周围的弹性土体相连，在弹塑性界面上将产生一定质点运动速度的扰动，扰动在周围无限弹性介质中传播而形成人工地震波。人工地震波的特征受到弹塑性界面扰动的控制，并受到传播介质特性的影响。

2 塌落触地振动速度峰值预测模型

2.1 塌落触地诱发塑性区的范围及其影响因素

图1 塌落体冲击作用下土体塑性区形态Fig.1 The shape of soil plastic zone under the impact of collapsed body

塌落冲击作用下，土体塑性变形区形态的主要影响因素包括以下几方面。

（1）塌落冲击能量

塌落体冲击能量是由建（构）筑物的势能转化而来，因此结构的高度、体积、平均密度等参数与土体塑性区形态间的相关性很强。

（2）触地接触面积

建（构）筑物塌落时与地面的接触面积大小直接影响接触面下土体的附加动应力，进而影响屈服区的范围。

（3）土体物理力学特征

土体的强度、天然容重、含水率等土体物理与力学参数是影响塑性区的重要因素，其中，土体干容重不仅反映了土体中固体颗粒排列的松紧程度，还能反映固体颗粒的矿物组成。干容重愈大的土体，颗粒排列愈紧密，孔隙度愈低，因此，土体的干容重可在一定程度上反映土体的强度特征。其次，土体的天然容重对塑性区质量有显著影响。另外，土体的干容重、天然容重在工程实践中是最容易获取的参数，而土体强度参数则存在离散性较高、测试速度慢的问题。因此，本文选取干容重和天然密度代表土体的物理力学特征。

2.2 土体塑性区深度预测模型

在研究强夯法土体加固技术时，Menard等［11］提出了加固影响深度的经验公式为

通过土地流转、开坑荒地等形式提高土地利用率，调整资源配置进行统一规划，产生乡村旅游所必须的自然景观。枞阳县周潭镇大山村坐落于在县的东部，与铜陵市接壤，全村有山场6300亩，其中森林面积占比达73.6%。在此丰富的生态基础之上，大山村于1995年创立约1600亩的“师范经果林”，用于种植板栗、茶叶、桃树等果树。同时因地处低山丘陵地带，为解决季节性缺水问题，2000年大山村又建立了一座库容量16万立方米的水库，直径约二十公分的钢制水管穿梭于山林之间，为成片的果林灌溉。水库位于山峰之间，倾泻而下的水形成一座微型瀑布，清明前后与上百亩的桃花一同吸引着周边游客前来游玩。

式中，H为加固影响深度（m）；W为夯锤重（t）；h为夯锤下落高度（m）。

Menard等［11］提出的（1）式并没有给出明确的物理意义，且方程量纲不统一，只能作为经验公式。张平仓等［12］应用量纲分析法，结合对土体加固深度影响因素的分析，建立了H的量纲分析式为

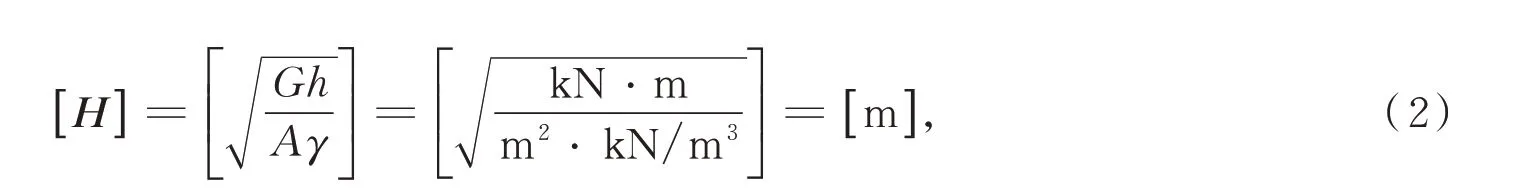
式中，G为塌落体重量，量纲为kN；h为塌落体质心高度，量纲为m；A为触地接触面积，量纲为m2；γ为土体的干容重，量纲为kN/m3；H为塑性区深度，量纲为m。因此，引入无量纲系数k，建立H的数学模型为

2.3 塌落触地振动速度峰值预测模型

设塌落体质量为m1，地面塑性区的质量为m2。碰撞前，塌落体的速度v1≠0，地面塑性区的速度v2=0；碰撞后，塌落体的速度v1=0，地面塑性区的速度v2≠0，则其动量守恒方程表示为

式中，m1、m2量纲为kg；v1、v2量纲为m/s。

因此，地面塑性区在碰撞后的平均速度可表示为

地面塑性区在获得初速度，沿着弹塑性分界面的法线方向产生扰动，进而以弹性波的形式向弹性区传递振动能量。根据以往的质点振动速度衰减模型［2-6］，距离振源R处的最大振动速度公式可以表示为

式中，ξ为衰减系数，对于土体取1.3～1.7。一般情况下平面触地方式产生应力峰值最大，因此R取计算点距离塌落边界的水平最小距离。

忽略冲击作用下塑性区被压缩时密度的变化时，接触面下土体塑性区的质量m2可近似表示为

式中，S为塑性区横截面面积，量纲为m2；ρ为塑性区土体的平均密度，量纲为kg/m3；l为塑性区的纵向长度，量纲为m。

由于塑性区面积形状特殊，为简化计算，将其简化为宽度与触地接触面宽度d相等，深度为H的矩形截面，则m2可表示为

式中，宽度d、深度H量纲均为m。

设倒塌建筑物重心处的触地速度完全由重力势能转化而来，则

根据式（6）、式（8）和式（9）得：

因为k为无量纲系数，设η=1/k2，（11）式改写为

式（10）～式（12）中，由于v1和v2的速度方向一致，因此计算得到的V R为质点合速度计算模型，而工程实践中需控制的是某个方向上的速度，因此，无量纲数值η可通过涵盖速度分解系数得到某一方向的振动速度峰值V R。其次，应指出的是，该公式及其衰减系数取值仅适用于建（构）筑物直接冲击地基土体而未采取缓冲减振防护措施的情况。

3 模型验证与讨论

为了验证塌落体触地振动速度峰值预测模型式（12）的有效性，对武汉江天大厦、衢州西安门大桥、武汉沌阳高架桥、山东济东高速［13］、六盘水某钢筋混凝土烟囱［14］爆破拆除工程实测振动监测数据进行了分析，由于原工程实施过程中土体密度、重度未进行测量，因此，各工程的未知参数均取了典型值，土体密度ρ取1 850 kg/m3，干容重取16 kN/m3，无量纲系数ξ取1.6，K取0.25，模型验证结果见表1。

由表1可知，在取土体参数近似值和无量纲系数估算值条件下，楼房、桥梁和夯锤时间的计算结果相对较吻合，预测振速/实测振速值在0.40～1.45范围。六盘水钢筋混凝土烟囱工程的预测振速/实测振速值在0.92～2.90范围。总体上，触地接触面较宽的工程模型的误差偏小，而触地接触面较窄的工程误差偏大。其原因可能是烟囱等高耸结构高度大、触地接触面窄，高速冲击下其下方土体塑性区形态与速度低触地接触面相对较宽的情况并不一致。

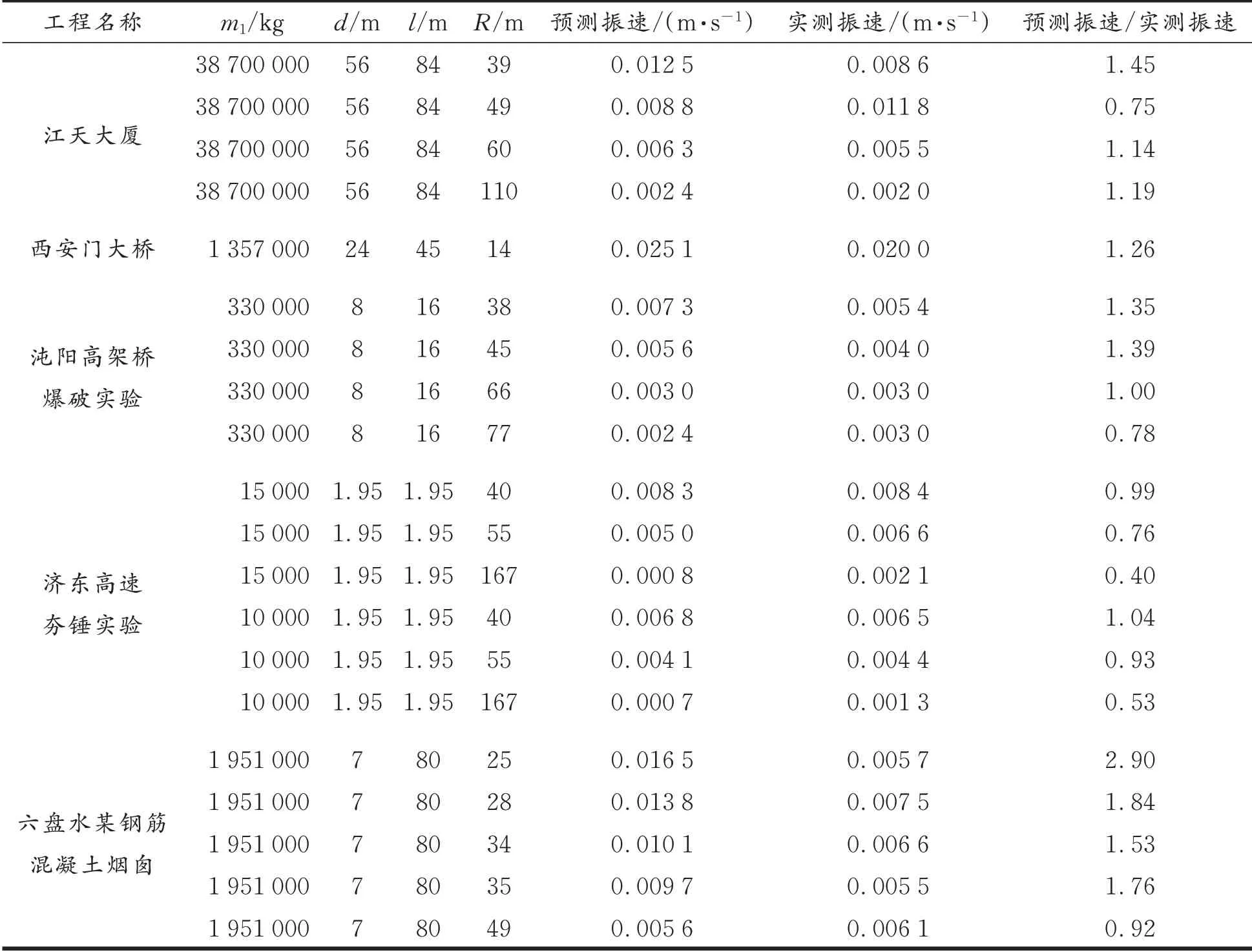
表1 模型验证结果Tab.1 Model validation results

因此，本文构建的塌落触地振动峰值预测模型为楼房等拆除爆破工程的安全校核提供参考，但需通过多个类似工程实测数据的回归和验证，以期在新爆破工程中确定合理的参数和系数。

4 结语

针对建（构）筑物爆破拆除工程塌落触地振动速度预测问题，分析了触地振动产生的机制以及主要影响因素，基于动量守恒理论和量纲分析方法，构建了塌落触地振动速度峰值的数学模型。对多个工程实测振动速度峰值数据的统计分析表明，对触地接触面较宽的工程，该模型的误差偏小，而对触地接触面较窄的工程误差偏大。总体上，该模型力学意义明确，形式简单，参数少，便于工程应用，可为楼房等宽接触面建（构）筑拆除爆破工程的安全校核提供参考，但需通过多个类似工程实测数据的回归和验证以确定合理的参数。