黎曼流形上三个微分算子各自在共形度量下的关系式

田大平，汪 敏

（江汉大学 人工智能学院，湖北 武汉 430056）

0 引言

散度算子、梯度算子和Laplace算子不仅是黎曼几何中非常重要的三个微分算子，而且在数学的许多其他分支学科中也扮演着举足轻重的角色。散度算子是作用在黎曼流形上的光滑切向量场上的线性映射，它将黎曼流形上的光滑切向量场映射成光滑函数。梯度算子是作用在黎曼流形上的光滑函数场上的一阶线性微分算子，它将黎曼流形上的光滑函数映射成光滑切向量场。将梯度算子与散度算子复合起来，便得到一个新的线性映射，即Laplace算子。在黎曼流形上，Laplace算子就是将散度算子作用于梯度算子的一个二阶椭圆微分算子［1-2］。因此，黎曼流形上的Laplace算子作用在光滑函数场上，将黎曼流形上的光滑函数映射成光滑函数。

对于散度算子和梯度算子在各类问题中的研究与运用已有许多结论，如文献［3］研究了一个包含散度算子的Dirichlet问题；文献［4］研究了基于散度算子和非线性分类器的红外小目标检测问题；文献［5］研究了具有非球相互作用邻域的非局部梯度算子及其应用；文献［6］研究了采用改良的Gabor滤波器、梯度算子和形态学分割工具来检测肺癌的问题；文献［7］研究了交互作用Fock空间上的梯度算子和散度算子。涉及Laplace算子的研究与应用同样也有非常丰富的成果，如文献［8］研究了Laplace算子在欧氏空间中的球坐标系与柱坐标系下的表达式；文献［9］研究了球坐标系与柱坐标系下作用于矢量函数的Laplace算子；文献［10］研究了Laplace算子在正交标架丛上的应用；文献［11］研究了Laplace算子在Yamabe流上的特征值的单调性应用。除了在数学的各分支学科上的应用外，在计算机科学、物理学等学科中都会涉及到Laplace算子的应用，如文献［12］研究了Laplace算子基于原子体积场对金属玻璃剪切转变区的预测。对于黎曼流形上的微分算子在共形的黎曼度量下关系式的研究，文献［13］借助共形的黎曼度量的Christoffel记号的关系式，已经推导出了黎曼流形上的光滑函数的Hessian在共形的黎曼度量下的关系式。

本文从黎曼几何的角度出发，运用黎曼流形上的散度算子、梯度算子、Laplace算子以及共形的黎曼度量的定义，通过计算，直接推导出这三个微分算子各自在共形的黎曼度量下的关系式。虽然文献［1］已经以习题的形式给出了黎曼流形上的Laplace算子在共形的黎曼度量下的关系式，并且引导读者利用共形的黎曼度量的Christoffel记号的关系式来证明这个关系式，这与本文定理3的部分结论一致，但是本文定理3的证明不借助共形黎曼度量的Christoffel记号的关系式，而是直接运用黎曼流形上的Laplace算子和共形的黎曼度量的定义来通过计算进行证明。

1 预备知识

设M是m维光滑流形，g和g͂是M上的两个黎曼度量。记g ij和͂ij分别为度量矩阵(gij)m×m和的逆矩阵中对应位置的元素。C∞(M)表示M上的全体光滑函数的集合。记ℵ(M)为M上的全体光滑切向量场（即C∞切向量场）的集合。对于任意的非负整数r和s，M上全体光滑的(r,s)型张量场构成的集合记作(M)。特别地，有

定义1［1］设M是m维光滑流形，称M上的一个光滑的一阶协变张量场为M上的一个1次微分式。

我们将光滑流形M上的全体1次微分式所组成的集合记作A1(M)，即

定义2［2］设M是m维光滑流形，称M上的一个光滑的反对称r阶协变张量场为M上的一个r次外微分式。

我们将M上的全体r次外微分式的集合记作A r(M)。根据定义，外微分式具有反对称性质，因此，当外微分式的次数r＞m=dimM时，此外微分式必为零。为简便起见，我们特别规定：M上的0次外微分式就是M上的光滑函数；M上的1次外微分式就是M上的1次微分式，也即为光滑的一阶协变张量场，即有

进一步地，令

从而，我们可以在A(M)上定义外微分运算。

引理1［1］设M是m维光滑流形，则在M上存在唯一的一个映射，即

使得对于任意的非负整数r，有d(A r(M))⊂A r+1(M),并且满足以下条件：

1）d是线性的，即对于任意的φ,ψ∈A(M),k∈R，有

2）∀φ=A r(M),ψ∈A(M),有

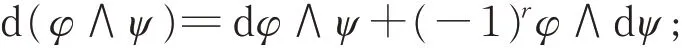
3）∀f∈A0(M)=C∞(M),df是f的微分；

4）d2=d∘d=0。

我们将这样的映射d称为外微分（算子）。

引理2［1］设(M,g)是m维黎曼流形，则在M上存在唯一的一个与黎曼度量g相容的无挠联络D，称为(M,g)的黎曼联络或Levi-Civita联络。

为了借助黎曼联络D在M上引入相关微分算子，我们现在假设(M,g)是m维有向黎曼流形。对于任意的X∈ℵ(M)，于是DX是M上的光滑的（1，1）型张量场。将DX进行缩并运算，便可以得到M上的一个光滑函数，称其为光滑切向量场X的散度，并记为divX，也就是说，divX=其中符号表示对一个张量场关于第一个反协变指标和第一个协变指标进行缩并运算。显然，div作为从ℵ(M)到C∞(M)的一个映射是线性的。

定义3［1］设X∈ℵ(M)，称由X→divX所确定的线性映射div:ℵ(M)→C∞(M)为黎曼流形(M,g)上的散度算子，并且称divX为切向量场X的散度。

为了求得散度算子的局部坐标表达式，假设(U;x i)是M的一个局部坐标系，并令则有

其中G=det(gij)。

设f∈C∞(M)，则借助黎曼度量g，可知df对应于M上的一个光滑切向量场，记作∇f，使得对于任意的X∈ℵ(M)，有

我们称切向量场∇f为光滑函数f在黎曼度量g下的梯度场。

定义4［1］称线性微分算子∇:C∞(M)→ℵ(M)为黎曼流形(M,g)上的梯度算子。

在M的局部坐标系(U;x i)下，设f∈C∞(M)，则有

我们将散度算子div作用于光滑函数f的梯度场∇f，便可得到一个从C∞(M)到C∞(M)的新的线性映射，记作

这是黎曼流形上的一个非常重要的微分算子。即对于任意的f∈C∞(M)，有

定义5［1］设(M,g)为黎曼流形，称线性映射Δ:C∞(M)→C∞(M)为M上关于度量g的Laplace算子。

在M的局部坐标系(U;x i)下，由式（1）与式（2）可得Laplace算子的局部坐标表达式为

定义6［1］设M是m维光滑流形，g和g͂是M上的两个黎曼度量。如果存在光滑的正函数λ∈C∞(M)，使得g͂=λ2g，则称g和g͂互为共形的黎曼度量，简称为共形度量。

2 定理及证明

本节将给出本文的主要定理，即黎曼流形M上的散度算子、梯度算子和Laplace算子各自在两个互为共形的黎曼度量下的关系式。并且根据这三个微分算子和共形度量的定义，通过计算完成对定理的证明。

为简便起见，下文中分别在每个微分算子的右下标位置加上符号g和g͂来表示黎曼流形M在相应的黎曼度量下的微分算子。

首先，给出黎曼流形M上的散度算子div在共形度量下的关系式，即有下面的定理。

定理1设M是m维黎曼流形，g和g͂是M上的两个共形度量。则对于任意的X∈ℵ(M)，在M的局部坐标系(U;x i)下，X在(M,g)上的散度和在(M,g͂)上的散度满足如下的关系式：

特别地，若λ=ep,p∈C∞(M),则式（4）成为

证明在M的局部坐标系(U;x i)下，由式（1）得

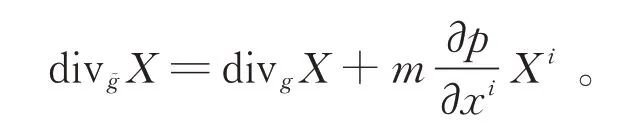
定理1得证。

其次，我们给出黎曼流形M上的梯度算子∇在共形度量下的关系式，即有下面的定理。

定理2设M是m维光滑流形，g和g͂是M上的两个共形度量。则对于任意的f∈C∞(M)，在M的局部坐标系(U;x i)下，f在(M,g)上的梯度和在(M,g͂)上的梯度满足如下的关系式：

特别地，若λ=ep,p∈C∞(M),则式（5）成为

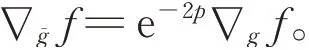
证明在M的局部坐标系(U;x i)下，由式（2）得

显然，若λ=ep,p∈C∞(M),则式（5）成为

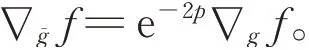
定理2得证。

最后，给出黎曼流形M上的Laplace算子Δ在共形度量下的关系式，即有下面的定理。

定理3设M是m维光滑流形，g和g͂是M上的两个共形度量，Δg和Δg͂分别是M上关于度量g和g͂的Laplace算子。则对于任意的f∈C∞(M),Δg f与Δg͂f满足如下的关系式：

特别地，若λ=ep,p∈C∞(M),则式（6）成为

证明在M的局部坐标系(U;x i)下，由式（3）得

显然，若λ=ep,p∈C∞(M),则式（6）成为

定理3得证。