考虑经济利益的泊位-岸桥联合调度

牟志为,傅恩圆

(天津大学管理与经济学部,天津 300072)

作为连接国际物流网络的重要节点,在过去的数十年里,世界主要港口的集装箱吞吐量持续增长,并有望在接下来的数年里继续保持增长势头,即使是在受到新冠疫情强烈冲击的2020年上半年,我国部分港口的集装箱吞吐量仍能够逆势增长[1]。这种迅猛的发展势头促使码头运营者为了提高集装箱码头的作业效率,一方面增加码头作业设备数量,另一方面更加重视制定合理的作业计划。作为码头的主要稀缺资源,泊位的分配情况和岸桥的调度情况影响到整个集装箱码头的作业效率,在很大程度上泊位的分配会影响到岸桥的调度。因此,考虑将泊位计划和岸桥计划综合起来进行分析,通过参数共享来制定联合调度计划,以代替之前独立地制定作业计划。

已有许多关于泊位-岸桥联合调度的研究,如Akio等[2]首先针对船舶动态到港下的泊位-岸桥调度问题,以船舶在港时间最小为目标,给予所有船舶同等的服务优先级并假设为每艘船舶服务的岸桥数固定;Young-Man等[3]最先研究了连续型泊位的泊位分配和岸桥调度问题,以集装箱的装卸成本加权总和最小化为优化目标,设计了一个两阶段的算法进行求解;李娜等[4]以待分配船舶的总在港时间最小为目标建立模型,考虑了岸桥交叉干扰等现实约束,利用Squeaky Wheel 优化方法,设计了一个启发式算法进行求解。

对于船舶公司来说,船舶在港时间较短有助于降低其自身运营成本,提高货物周转速度。但在泊位-岸桥调度问题中,船舶的装卸时间实际上取决于岸桥的分配结果。对于码头运营者而言,更希望看到其昂贵的码头资源得到充分利用,一味致力于减少船舶在港时间,势必需要将更多的岸桥调配给同一艘船只,将会带来岸桥移动成本的明显提高以及码头泊位利用率的降低。因此,后期的研究者在此基础上提出了更多优化目标,如Frank等[5]研究了装卸作业中岸桥的边际效率问题,认为随着为船只服务的岸桥数量增加,其边际效率下降,他们以最小化所有到港船舶的总服务成本为目标建立了泊位-岸桥调度模型;杨华龙等[6]认为想要达到系统最优,必须考虑岸桥利用率,因此建立了目标为船舶在港时间最小和岸桥利用率最高的模型,并针对该模型使用挤压算法求解;Yavuz等[7]综合分析了船舶偏离偏好泊位成本、等待泊位的时间成本和船舶滞期成本,对不同规模的问题进行求解;杨劼等[8]从为船舶提供的所有服务的成本入手,致力于减少船舶等待泊位成本、偏离偏好泊位成本、推迟离港的时间成本和岸桥移动成本。

综合已有研究分析,早期研究者考虑的因素较为单一,片面追求在港时间最小化既不符合码头方的利益,也无法满足船舶方多方面的需求。后期的研究者从码头服务质量、船舶服务成本、客户满意度等方面入手,但是更多的还是站在船舶公司的角度出发来寻找最优解或满意解。码头运营者和船舶公司作为泊位-岸桥调度问题的利益双方,均陷入了非零和博弈的状态。在双方都只关注其自身经济利益的前提下,船舶公司希望能够降低其在港时间和运营成本,而码头运营者则期望从到港船舶身上攫取更多利润。当然,二者可以合作共赢,找到这个合作博弈问题的帕累托解集具有重要现实意义。研究先从码头运营者角度出发,在锚地停泊、引航、泊位停泊、装卸作业、集卡运输等环节进行分析,厘清船港双方在各个环节上的利益关系,找到整个系统的痛点,再研究如何兼顾双方,以制定更切合实际、更合理的泊位-岸桥联合调度计划。

1 建立模型

在抵港之前,船舶需要将自身船型、计划到港时间、需要装卸作业量等信息报备给码头,根据这些信息,码头在计划周期内制定作业计划,包括船舶在指定时间停靠、停靠于指定泊位、由指定岸桥进行装卸作业等。船舶到港后的作业流程如图1所示。

图1 到港船舶作业流程Fig.1 Operation flow chart of the arriving ships

港口经营服务性费用参考我国2019年修订的《港口收费计费办法》,因为在锚地停泊费用远小于在港内停泊费用,因而设定船舶到港后,假如为其分配的泊位或岸桥不可用,船舶将在锚地等待,港口按照停泊时间和船舶吨位收取锚地停泊费。在确认分配的泊位和岸桥均可用后,进行引航作业,需要移动的岸桥向预停靠泊位移动,船舶进入港口并停泊在指定泊位。在这个过程中,港口按照船舶吨位和引航距离收取引航费用。靠泊之后,由分配的岸桥对船上集装箱进行装卸作业,港口按照船舶停泊时间和吨位收取停泊费,并按照自定标准(一般包括作业量、使用岸桥数量等)收取港口作业包干费,集装箱从船上卸下后由集卡运送至堆场堆存,港口按照自定标准收取库场使用费;港口还将根据集装箱型号和数量收取港务费及港口设施保安费,但货物信息确定后二者相当于固定费用,因此模型中不再考虑。同理,库场使用费也根据集装箱型号和数量收取,模型仅考虑码头方因未安排船舶进入偏好泊位而额外付出的运输成本。经过分析,各环节产生费用及影响因素如表1所列。

表1 港口停泊各环节费用及影响因素

1.1 模型假设

该模型建立在离散型泊位布局的码头上,即一定长度岸线被划分为若干个大小各异的泊位,每个泊位拥有不同的长度和水深,能够满足不同类型船只的需要。模型假设如下:(1)所有船舶在时间和空间上不能重叠;(2)所有岸桥在不同时段的工作效率相等,但当多台岸桥同时在一艘船作业时,相互之间会有影响;(3)所有岸桥直线分布于岸线上,不能交叉跨越作业,默认岸桥移动在引航时间内完成;(4)分配给所有船舶的岸桥数量在作业过程中保持不变;(5)每艘船舶能靠泊一次且必须靠泊一次,并且不能移泊;(6)每艘船舶都有偏好泊位,使得泊位与该船货物应当储存的堆场之间距离最短;(7)每艘船舶都有固定的安全水深、安全船长以及最小和最大的可分配岸桥数量;(8)所有船舶从锚地到特定泊位的引航时间都是已知和固定的,不考虑潮汐、船只大小的影响因素;(9)码头必须在计划周期内完成所有到港船舶的装卸作业。

假设(1)是离散型泊位码头的基本要求;假设(2)参考了文献[5]中的研究,在模型中设定多台岸桥共同工作的相互影响系数;假设(3)保证为船舶分配的岸桥必须相邻,满足客观实际条件;假设(4)被证明[9]能够为实际操作提供保守的时间表,因为基于动态岸桥数量的理论分析往往带来大量的岸桥移动,在实际中会很快偏离理论计算;假设(5)保证船舶必须靠泊且只能靠泊一次,模型不考虑移泊;假设(6)规定船舶拥有偏好泊位,停靠在偏好泊位能够提高集卡运行速度,相较于偏好泊位,码头将集装箱从其他泊位运输到堆场,需要付出额外运输成本;假设(7)和假设(8)规定模型中考虑到的参数已知且固定;假设(9)对码头制定作业计划施加限制,相应地在算例实验时会减少计划周期后期到船概率,最后数个小时不再到船。

1.2 参数符号

模型中涉及的符号表示如下:

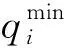
1.3 决策变量

模型中的决策变量为:

pi为船舶i的开始引航时间,整数;bi为船舶i的靠泊时间,整数;li为船舶i的离港时间,整数;Bi为船舶i的停泊泊位,整数;Qi为分配给船舶i的岸桥数量,整数;Uijqt∈{0,1},当船舶i在泊位j在时间t被q台岸桥服务时,取值为1,否则为0;σij∈{0,1},当船舶i在泊位j被服务时,取值为1,否则为0。

为了方便在模型中表示,定义了一些变量,它们都可以轻易用决策变量Uijqt表示出来,变量如下:

θit∈{0,1},当船舶i在时间t被服务时,取值为1,否则为0;δijt∈{0,1},当船舶i在时间t在泊位j被服务时,取值为1,否则为0。

1.4 目标函数

最大化码头经济利益的目标函数为

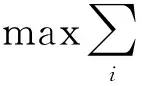
α3vi(li-bi)+α4wi-α5Qi(li-bi)+

α6wiDBiPi),

(1)

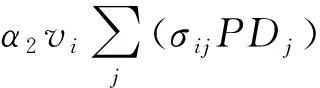
1.5 约束条件

模型中的约束条件为

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(t+1)·θit≤li, ∀i,t

(11)

t·θit+H·(1-θit)≥bi, ∀i,t

(12)

pi,bi,li∈{ai,…,H}, ∀i

(13)

(14)

(15)

Uijqt,σij,θit,δijt∈{0,1}, ∀i,j,q,t

(16)

式(2)定义了船舶靠泊时刻和引航时刻的关系,表示船舶经过引航作业后靠泊;式(3)引入多台岸桥在同一艘船上工作时的影响指数,表示必须满足船舶装卸作业所需台时数;式(4)表示对于所有船舶来说,有且只有一次靠泊机会且必须靠泊一次;式(5)和式(6)表示泊位要满足船舶的安全水深和安全船长;式(7)表示岸桥数量约束;式(8)表示为每艘船分配的岸桥数量要大于等于其最小岸桥数量且不超过其最大岸桥数量;式(9)表示所有船舶在时间和空间上不能重叠;式(10)～(12)定义了船舶的靠泊时间和离港时间;式(13)表示所有环节均在计划周期内完成;式(14)～(16)定义了决策变量的相互关系和取值范围。

2 求解算法

泊位-岸桥联合调度问题属于NP-hard问题,已有多项研究针对它提出了包括精确解算法和启发式算法的不同算法进行求解。Salhi等[10]在研究中同时使用了商业化求解软件CPLEX和遗传算法,证明对于较大型实例只有使用启发式算法才能在合理的时间内找到最优或者接近最优的解决方案。为了更加贴近实际情况,研究采用了改进的遗传算法[11]对模型进行求解,包括采用改进的锦标赛选择算子对种群进行选择,基于sigmoid函数的交叉和变异率来使算法获得更好的收敛性以及跳出局部最优解的能力。算法的具体流程如下:

(1) 根据编码规则初始化Nind个个体的种群;

(2) 若满足停止条件,则算法结束,输出最终结果,否则继续执行;

(3) 对当前种群进行统计分析,记录其最优个体、平均适应度等,并计算当前交叉率和变异率;

(4) 按照当前交叉率对当前种群的Nind个母体进行交叉操作;

(5) 按照当前变异率对这Nind个交叉后的个体进行变异;

(6) 将父代种群和交叉变异得到的种群进行合并,得到规模为2Nind的种群;

(7) 从合并的种群中根据选择算法选择出Nind个个体,得到新一代种群;

(8) 回到(2)。

2.1 编码方式

对于决策变量Uijqt来说,有3个决定因素,分别是靠泊位置Bi、分配的岸桥数量Qi和开始引航作业时刻pi。因此针对模型中这3个决定因素,使用3条染色体进行编码,如图2所示。图2中船舶2停泊在4号泊位,分配给它的岸桥数为2台,在时间3进行引航作业。

图2 染色体编码方式示例Fig.2 Example of the chromosome coding method

在编写代码实现算法时,先对输入的船舶信息进行分析,根据约束条件(2)(5)(6)(8)(13)得到所有船舶能够停靠的泊位范围、可接受的岸桥数量范围以及可以进行靠泊的时间范围等数据,以此对每个基因位置的取值范围设定限制,避免产生大量不可行解。在执行交叉和变异操作后也对每个基因位置进行检查,修复不可行的染色体。

2.2 适应度函数

该模型是为了找到计划周期内每艘到港船舶的最佳停泊位置、最佳停泊时间以及最佳分配岸桥数量,使码头运营者得到经济利润的最大化。因此,将模型的目标函数设定为遗传算法的适应度函数:

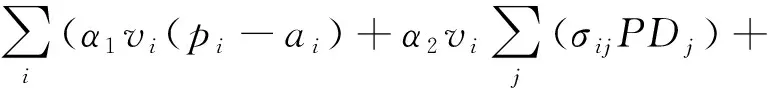
α3vi(li-bi)+α4wi-α5Qi(li-bi)+

α6wiDBiPi)。

(17)

2.3 选择算子

研究采用了改进的锦标赛选择法,选择算子的具体步骤如下:

(ⅰ)首先从父代种群和交叉变异得到的种群合并的种群中(规模为2Nind),按照适应度大小进行排序,将位于优势位置的前1/4的个体直接选择进入下一代种群;

(ⅱ)在剩余的个体中随机选择n个个体,将其中适应度最好的个体选择进入下一代种群;

(ⅲ)重复步骤(ⅱ),直到新种群的规模达到Nind。

2.4 交叉和变异操作

遗传算法中的交叉概率Pc和变异概率Pm对算法的收敛性影响重大。对于增强的精英保留算法来说,在算法的初期,种群适应度的方差较大,而在算法后期种群适应度的方差变小,甚至产生多个相同个体。因此,参照文献[11]中的方法,基于sigmoid函数设计了交叉概率Pc和变异概率Pm,其公式分别为

(18)

(19)

其中:k1、k2是参数,可以根据实际问题进行取值;Dx为种群适应度方差;Pcmax、Pcmin分别为种群的最大、最小交叉概率;Pmmax、Pmmin分别为种群的最大、最小变异概率。按照式(18)和式(19),在进化初期,种群的适应度方差较大,相应地Pc也会较大,而Pm则较小,在进化后期反之。利用种群适应度方差进化过程中的变化特点,满足了算法前后期对交叉、变异概率值的不同要求。sigmoid函数图像如图3所示。

图3 sigmoid函数图像Fig.3 Graph of sigmoid function

3 数值实验

参考某集装箱码头数据,该码头岸线长1 700 m,拥有6个泊位,20台岸桥,其中200 m泊位2个,300 m泊位3个,400 m泊位1个。将到港船舶按照安全船长分为3个等级:小型、中型和大型,假定所有泊位水深能够满足所有船舶的停靠要求。船舶参数设置如表2所列,其中小型船舶参数参考3 000TEU集装箱船,中型船舶参数参考标准巴拿马型集装箱船,大型船舶参数参考12 000TEU集装箱船。按照中型船舶占60%,其他2种船舶各占20%的比例随机生成分别包含20、25、30艘船的算例。

表2 船舶参数设置

所有集装箱均折算成装载一般货物的20英尺标准TEU计算,所有船只按照国际航线船舶收费基准费率收费。计划周期为72 h,设置船舶只在前60 h到港,之后不再有船舶到港。参考《港口收费计费办法》和某港口收费标准设置参数如下:α1=2.1,α2=1.8,α3=10,α4=500,α5=20 000,α6=10。单个岸桥单独作业下的工作效率η=300箱/h,β=0.9,Pcmax=1,Pcmin=0.5,Pmmax=0.3,Pmmin=0.001,Dsg根据泊位之间的距离确定。算法采用Python语言编程,在英特尔Core i5-8400 2.80 GHz六核处理器、8 GB内存和Win 10操作系统下完成实验。通过实验选取算法参数分别为种群个数Nind=100,最大进化代数为500代。为了进行对照,在模型的基础上增加以最小化所有船舶总在港时间为目标的目标函数作为对照,其函数表示为

(20)

再分别以最大化码头运营者经济利益、最小化码头运营者利益、最大化所有船舶总在港时间和最小化所有船舶总在港时间为目标进行实验,各算例及各目标结果如表3所列。

表3 数值实验求解结果Table 3 The results of numerical experiment

从表3中可知,针对实验生成的3个算例,当以最大化码头运营者的经济利益为优化目标时,船舶在港时间大幅变长,但还是明显小于以最大化在港时间为目标时得到的解。而当以最小化经济利益为目标时,得到的结果基本与目标为最小化船舶总在港时间无异,甚至有时能得到使船舶在港时间更小的解。

4 结语

对离散型泊位布局的集装箱码头进行了泊位-岸桥联合调度问题的研究,在目标函数中考虑了船舶在锚地停泊、引航作业、装卸作业等环节产生的费用以及码头运营者因此付出的成本。在假设船舶装卸作业中岸桥数量不变以及考虑多台岸桥一起工作时使其效率边际递减的情况下,以码头运营者经济利益为判断参考建立整数规划模型并设计算法求解。为了对照,同时以船舶在港时间为判断参考,分别对2种目标函数进行最大化和最小化求解。通过数值实验证明了模型和算法的有效性,数值实验表明,一味延长船舶总在港时间并不能使码头运营者实现经济利益最大化,但以最小化船舶在港时间为目标进行优化,基本上意味着码头运营者同时也最小化了自己的当前经济利益,这显然是码头方不能接受的。然而,一味追逐当前经济利益的最大化,会使船舶在港时间大幅增加,这是船方不能接受的。因此,应该将码头方经济利益和船舶在港时间或者其他标准联合起来考虑,通过设置权重来寻找双方比较满意的解,这需要进一步的研究。