基于WASD神经网络的日本国债预测结果与分析

李立天,郑晓燕,薛忠贤,张雨浓,邱斌斌

(1.中山大学计算机学院,广东 广州 510006; 2.中山大学人工智能学院,广东 珠海 519082)

政府债务也叫国债,是指国家按照一定的债务发行规则向社会发行的债务,当政府的财政收入不足以偿还财政支出时,可以通过发行债务来平衡收支[1]。日本中央政府债务发行的规模,在一定程度上能够反映中央政府的财政状况。在过去的20年里,日本国债总额出现了大幅度增加,从1996年6月的334.130 9万亿日元增长到了2016年12月的1 066.423 4万亿日元。日本财务省官网公布的数据显示,截至2020年6月底,国债总额已经达到1 159.028 9万亿日元[2]。日本国债和国民生产总值(GDP,gross domestic product)的比值已经明显高于其他发达国家,2018年该比例达到239%,这一数字远远高于在欧债危机蔓延时期发生债务危机的五国[2-3]。为了预估未来的财政风险并协助日本中央政府制定更好的财政政策,需要对日本国债的规模进行预测。

由于日本国债可参考的样本数据较少,同时影响日本国债的因素也较为复杂,所以使用传统的数据建模方式对其进行预测是不合适的。如使用BP神经网络[4-5]、RBF神经网络[6]和最小二乘法[7]进行预测,其要求更加多的训练数据才会有很好的预测结果。为了较好地对未来日本国债规模进行预测,研究中使用了权值和结构确定(WASD,weights and structure determination)算法训练切比雪夫神经网络[8-9],并利用训练效果最好的WASD神经网络对日本国债规模进行了短期的预测。从2017年3月—2020年6月一共14个季度的预测结果与日本财务省官方公布数据的最大相对误差仅为3.96%,说明WASD神经网络的预测性能良好并且此方法有效。在此基础上,利用预测性能最好的神经网络对2020年9月—2022年12月一共10个季度的日本国债规模进行预测。

1 WASD神经网络模型

由于神经网络内在的非线性性、自适应能力和高容错性,神经网络目前已经广泛运用于解决各种现实问题,例如人口预测、股票预测、模式识别等[10-11]。传统的误差回传神经网络采用过程冗长的迭代方式,在实际的使用中,往往需要耗费大量时间[12-13]。为此,张立等[14]提出利用混沌粒子学算法对BP神经网络的权值优化。这一方法提高了模型的预测精度,但模型收敛所耗的时间量依旧很大,而WASD神经网络的权值是通过求解矩阵伪逆得到的,避免了通过反复迭代才能得到网络较优权值的冗长训练过程。因此我们采用WASD神经网络[15]对日本中央政府债务(TCGD,total central government debt)规模进行预测。

1.1 神经网络模型

研究中使用的WASD神经网络的结构[15]如图1所示,该神经网络包括3层:输入层、隐藏层和输出层,其中输入层和输出层都各有1个由线性恒等函数激活的神经元,隐藏层中有N个由切比雪夫多项式激活的神经元[16-17]。为了降低神经网络训练和计算的复杂程度,我们将输入层到隐藏层的连接权重设为1,隐藏层到输出层的连接权重设为ωj(j=1,2,…,N),ωj是需要进行调整的。此外,所有神经元的阈值都设为0。我们只需要关注如何调整隐藏层神经元的个数以及连接隐藏层和输出层之间的神经元的权值。与此同时,以上所有的设置都需要保证此神经网络的预测性能。

图1 3层WASD神经网络结构Fig.1 Structure of three-layer WASD neural network

1.2 切比雪夫多项式

实验过程中,我们发现第一类切比雪夫多项式在多项式插值和逼近上有良好的性能[18]。因此,使用第一类切比雪夫多项式作为WASD神经网络隐藏层的激励函数[15]。

定义1第一类切比雪夫多项式

对于一个输入x(x∈[-1,1]),第一类切比雪夫多项式的表达式定义为

(1)

我们使用的WASD神经网络利用切比雪夫正交多项式对未知的函数进行逼近。当输入x满足x∈[-1,1]时,对一个未知的函数y=f(x),有

y=f(x)=ω1φ1(x)+ω2φ2(x)+…+ωNφN(x)=

(2)

用于拟合未知函数的切比雪夫多项式有N个。

1.3 权值直接确定法

WASD神经网络主要包括2个算法:权值直接确定(WDD,weights direct determination)算法和结构选优确定(SSD,structure selective determination)算法。在训练过程中,隐藏层神经元的个数N由SSD确定,神经元个数N的确定过程将在下一节叙述,而连接隐藏层和输出层的权值ωj由WDD得到。对图1中的3层WASD神经网络,取M对数据S={(xi,yi)|i=1,2,…,M}作为训练数据集,则权值列向量W、输入受激励矩阵φ和期望(目标)输出向量γ的定义分别为

(3)

(4)

(5)

则神经网络的权值列向量的最优解可确定为

W=(φTφ)-1φTγ,

(6)

其中:(φTφ)-1φT是矩阵φ的伪逆,在MATLAB中可以用pinv(φ)计算得到。

2 WASD神经网络的训练和校验

首先我们需要构建一个WASD神经网络,然后利用TCGD数据集对这个神经网络进行训练,并且通过WASD算法确定神经网络的最优结构。最后利用一个校验数据集对神经网络进行校验。

日本财务省每个季度都会在其官网公布债务数据。为了保证此神经网络预测结果的真实性,我们把从日本财务省官网中获取的数据作为神经网络的样本数据集。研究使用1996年6月—2016年3月的数据对神经网络进行训练,使用2016年6月—12月的数据对训练后的神经网络进行校验。这里需要引入神经网络的均方差(MSE,mean square error)这一概念。

定义2均方差(MSE)

(7)

需要说明的是此神经网络的输入是TCGD数据中的时间(例如1996年6月),输出是TCGD数据中的债务总额(例如334.130 9万亿日元)。由上述可知,隐藏层的神经元是由第一类切比雪夫多项式激活,而第一类切比雪夫多项式要求输入的值域为[-1,1]。因此,需要在数据输入神经网络之前,对输入的日期进行预处理。

利用位于区间[-1,1]的无单位归一化因子α将时间间隔区间[1996/6,2016/12]归一化到[-1,α]。在以前的工作中,发现归一化因子α对神经网络的数据拟合效果有一定的影响[15-17],因此找到一个合适的归一化因子α也很有必要。我们发现对每一个具体的α值,可以计算出对应的MSEmin以及相应的隐藏层神经元个数Nmin。那么当找到最优的α值后,也可以找到一个对应的MSEmin和最优的隐藏层神经元个数Nmin,从而确定神经网络的最优结构。

前面利用训练数据集对神经网络进行了训练,接着需要对此神经网络的预测能力进行校验,这里使用的是位于时间区间[2016/6,2016/12]的TCGD数据。和之前的训练一样,在校验神经网络之前,需要对输入数据进行预处理。

定义3校验误差

(8)

其中:K表示校验数据集中数据对的个数(K=3);yj和γj分别表示对应于输入xj神经网络的输出和期望输出。

当e的值越小,说明神经网络的预测能力越好。然后比较所有的归一化因子α(α∈[-1,1])对应的校验误差e,从而根据最小的校验误差e确定α,理论上此时神经网络具有最优的预测性能。归一化因子α和对应的具有最优结构的神经网络的校验误差之间的关系如图2所示。不同的归一化因子的值,将导致神经网络具有不同的预测性能。图2中标记了全局最小点和3个局部最小点。标记的全局最小点和3个局部最小点的归一化因子α的值以及对应的最优神经网络结构的隐藏层神经元个数N和校验误差e如表1所列。注意理论上全局最小点对应的神经网络就具有最优的预测性能,但每一个局部最小点在周围的点中有最小的校验误差,因此这些局部最小点也值得注意和分析。文献[15]中对标记的全局最小点和局部最小点进行了分析,并确定了最佳神经网络对应的归一化因子的值是全局最小点α=-0.999。由表1可知,最佳的神经网络中隐藏层神经元的个数为4,校验误差e=0.005 3为全局最小。

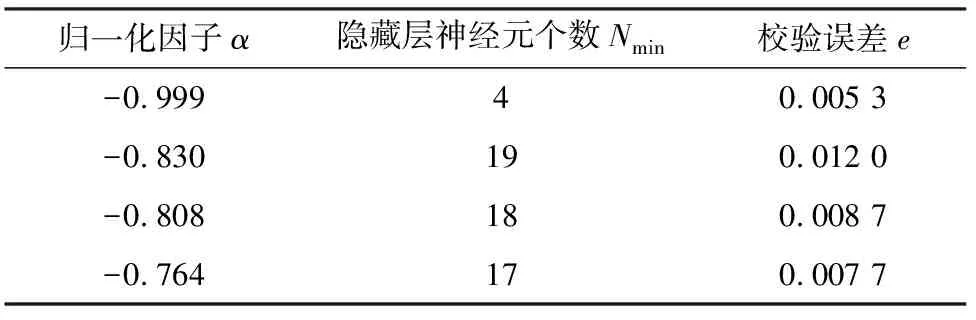
表1 归一化因子α的全局最小值与局部极小值对应的神经网络的隐藏层神经元个数和校验误差

图2 归一化因子α与具有最优结构的神经网络模型的校验误差之间的关系Fig.2 Relationship between normalization factor α and validation error of neural network model with optimal structure

3 WASD神经网络的预测结果对比

对标记出来的全局最小点和局部最小点进行分析,我们认为全局最小点对应的神经网络具有最佳的预测性能。理论上,全局最小点对应的神经网络的校验误差是最小的,数据拟合能力是最好的,最有可能得到最准确的预测结果。利用这个神经网络预测了2017年3月—2020年6月一共14个季度的日本国债规模,与日本财务省官网公布的真实数据对比见表2。由表2可以看到从2017年3月—2020年6月,预测数据和真实数据的相对误差很小,最大的相对误差只有3.96%。说明最佳预测模型的预测性能较好,也充分说明了将WASD神经网络应用于日本国债规模的预测上是十分准确和可靠的,并且预测结果是有意义的。

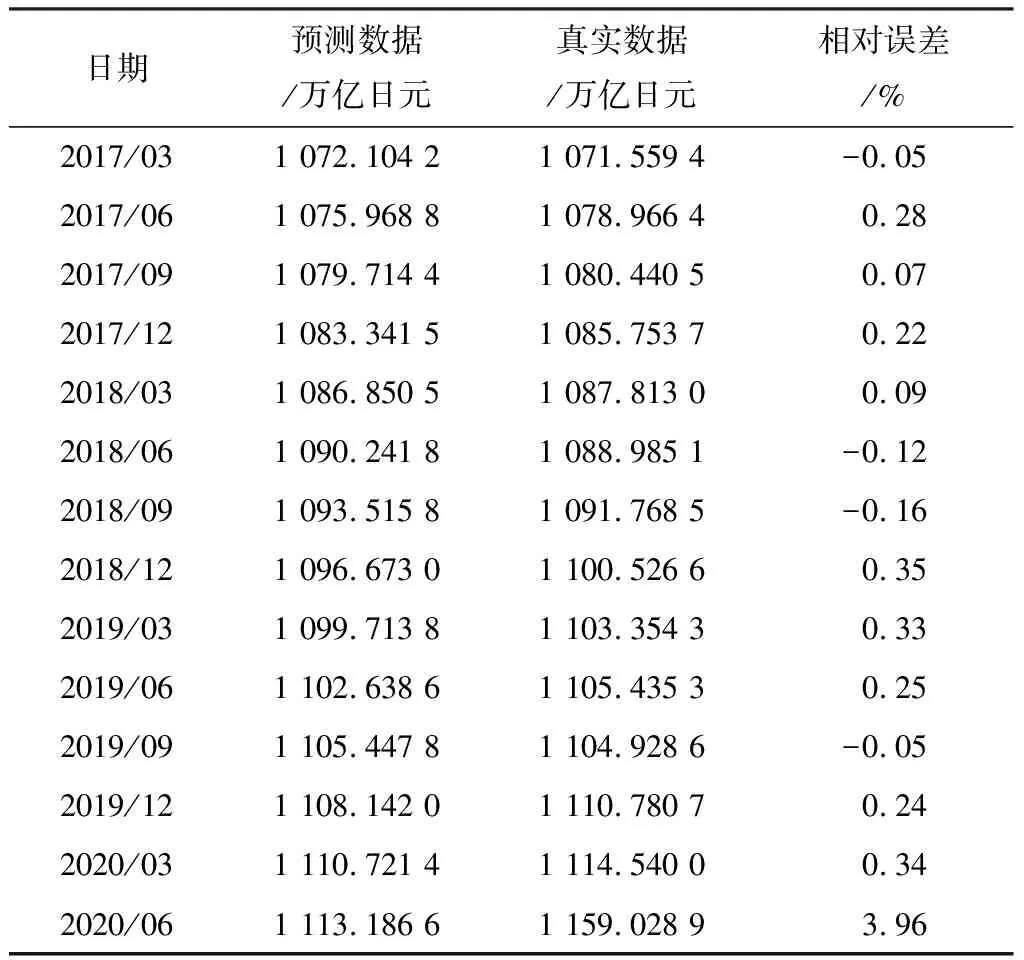
表2 理论最佳模型预测数据与真实数据回顾对比

经过与官方公布的2017年3月—2020年6月的数据进行比对,确定此神经网络的预测结果具有一定的价值,所以用更多的数据对神经网络进行训练。用新训练出来的理论最佳模型以及原来的理论最佳模型对接下来的10个季度(2020年9月—2022年12月)进行预测,得到的预测结果如表3所列。

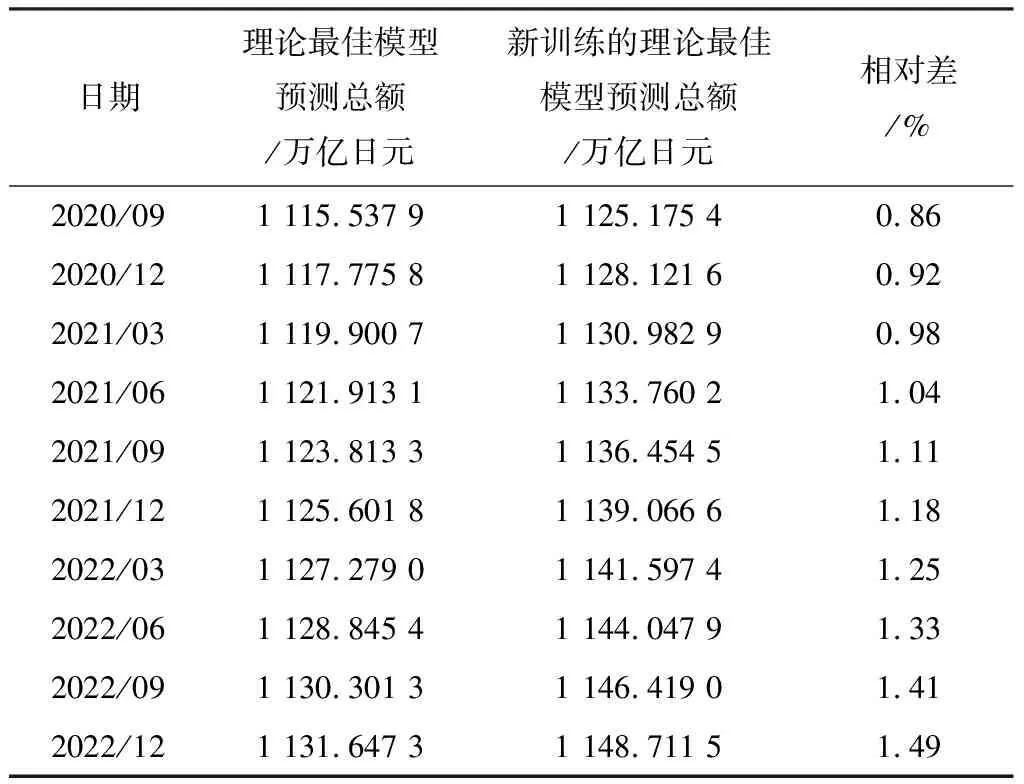
表3 理论最佳模型和新训练的理论最佳模型对日本中央政府债务规模未来预测数据及相对差

从日本财务省官网公布的真实数据上来看,除了个别季度(例如2008年6月、2008年9月、2014年9月、2015年9月、2020年6月)比前一个季度的数据有所下降或大幅上升以外,日本中央政府的债务规模总体上是缓慢上升的。预测数据和真实数据的变化趋势大体是一致的,但在具体的涨幅上有细微的差别,所以导致预测数据和真实数据之间存在微小的误差。经过对神经网络更进一步地训练,新的预测结果显示2个模型的预测结果的数据变化趋势相同,但在具体的数值上存在微小的相对差。我们认为未来的变化趋势仍是缓慢上升的,并且具体的数值可能在2个模型的预测值附近浮动,但仍有可能在个别季度出现轻微的下降。当然也可能因为某些现实因素(例如日本国内外金融环境变化、日本政府有力的财政政策以及重大自然灾害等)导致数据出现其他的变化趋势。

4 结语

在过去的20年间,日本国债规模快速增长,其国债与国民生产总值的比值明显高于其他发达经济体。为此,评估日本政府债务风险,对日本国债未来规模的预测具有一定的意义。利用日本财务省官方网站公布的1996年6月—2016年12月的日本国债规模数据对WASD神经网络进行训练和校验,并在此基础上完成了2017年3月—2020年6月共14个季度的日本国债规模的预测。最佳训练模型预测结果表明日本国债规模未来的变化趋势为缓慢上升,从2017年3月—2020年6月的预测结果与真实数据的相对误差在4%以内,体现了该方法的准确性和有效性。通过更进一步的训练和预测,结果表明在短期内(2020年9月—2022年12月)日本国债规模仍将缓慢上升。为此,未来日本政府财政政策应会继续偏于稳健,短期内不会出现债务危机。同时,WASD神经网络也可继续应用于未来国债规模的预测。当日本政府或其他国家政府认识到未来短期可能出现的趋势时,就可以制定出有效的财政政策规避风险,控制国债增长率,并做好应急准备。